lesson2-完全图、补图和顶点度
(一)、完全图、偶图与补图
1、每两个不同的顶点之间都有一条边相连的简单图称为完全图 (complete graph).在同构意义下,n个顶点的完全图只有一个,记为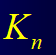

2、所谓具有二分类(X, Y)的偶图(或二部图)是指一个图,它的点集可以分解为两个(非空)子集X和Y,使得每条边的一个端点在X中,另一个端点在Y中.
完全偶图是指具有二分类(X, Y)的简单偶图,其中X的每个顶点与Y的每个顶点相连,若|X|=m,|Y|=n,则这样的偶图记为 Km, n 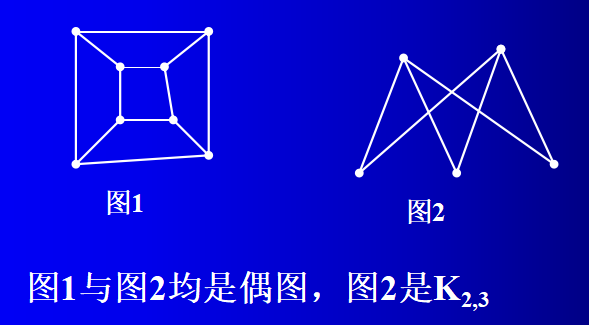
偶图是一种常见数学模型
例1 学校有6位教师将开设6门课程。六位教师的代号是xi(i=1,2,3,4,5,6),六门课程代号是yi (i=1,2,3,4,5,6)。已知,教师x1能够胜任课程y2和y3;教师x2能够胜任课程y4和y5;教师x3能够胜任课程y2;教师x4能够胜任课程y6和y3;
教师x5能够胜任课程y1和y6;教师x6能够胜任课程y5和y6。请画出老师和课程之间的状态图。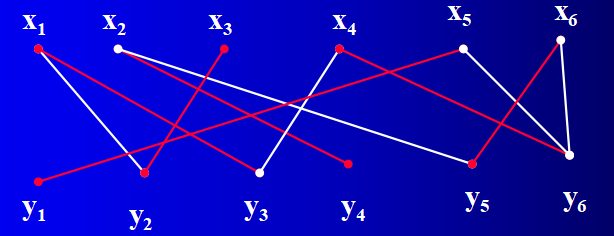
3、对于一个简单图G =(V, E),令集合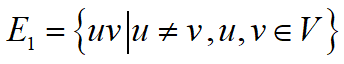
则称图H =(V,E1\E)为G的补图,记为
例如,下面两个图互为补图。
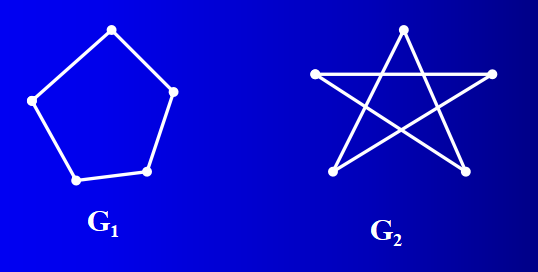
补图是相对于完全图定义的。补图是图论中经常涉及的概念,在图论研究中有重要的作用
如果图G与其补图同构,则称G为自补图。
定理:若n阶图G是自补图(  ),则有:
),则有:
证明:n阶图G是自补图,则有:
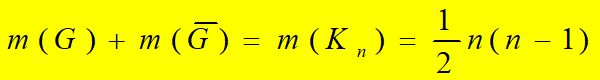
所以:
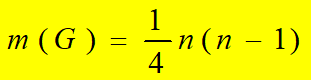
由于n是正整数,所以: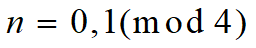
自补图是很有意义的图类。它在对角型拉姆齐数方面的研究、关于图的香农容量的研究、强完美图方面的研究等都有重要作用。
例2 在10个顶点以下的简单图中,哪些阶数的图可能为自补图?画出8阶的4个自补图(共10个)。
(二)、顶点的度与图的度序列
1、顶点的度及其性质
G的顶点v的度d (v)是指G中与v关联的边的数目,每个环计算两次。 分别用δ(G)和Δ(G)表示图G的最小与最大度。
奇数度的点称为奇度点,偶数度的顶点称偶度点。
设G = (V, E)为简单图,如果对所有 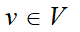 ,有d (v) = k,称图G为k-正则图
,有d (v) = k,称图G为k-正则图
定理: 图G= (V, E)中所有顶点的度的和等于边数m的2倍,即:
证明:由顶点度的定义知:图中每条边给图的总度数贡献2度,所以,总度数等于边数2倍。
注:该定理称为图论第一定理,是由欧拉提出的。欧拉一生发表论文886篇,著作90部。该定理还有一个名字:“握手定理”。
推论1 在任何图中,奇点个数为偶数。
证明:设V1,V2分别是G中奇点集和偶点集.则由
握手定理有: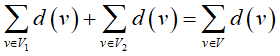 是偶数,由于
是偶数,由于 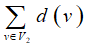 是偶数, 所以
是偶数, 所以  偶数,于是
偶数,于是 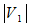 是偶数。
是偶数。
推论2 正则图的阶数和度数不同时为奇数 。
证明 : 设G是k-正则图,若k为奇数,则由推论1知正则图G的点数必为偶数
例4 Δ与δ是简单图G的最大度与最小度,求证: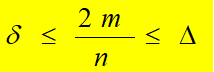
证明:由握手定理有: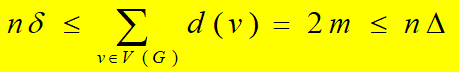 所以有:
所以有: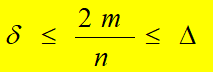
2、图的度序列及其性质
一个图G的各个点的度d1, d2,…, dn构成的非负整数组(d1, d2,…, dn)称为G的度序列 。任意一个图G对应唯一一个度序列,图的度序列是刻画图的特征的重要“拓扑不变量”。
图G 的“拓扑不变量”是指与图G有关的一个数或数组(向量)。它对于与图G同构的所有图来说,不会发生改变。
定理:非负整数组(d1,d2,…., d n)是图的度序列的充分必要条件是: 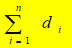 为偶数。
为偶数。
证明:必要性由握手定理立即得到。如果 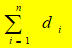 为偶数,则数组中为奇数的数字个数必为偶数。按照如下方式作图G:若di为偶数,则在与之对应的点作di/2个环;对于剩下的偶数个奇数,
为偶数,则数组中为奇数的数字个数必为偶数。按照如下方式作图G:若di为偶数,则在与之对应的点作di/2个环;对于剩下的偶数个奇数,
两两配对后分别在每配对点间先连一条边,然后在每个顶点画dj-1/2个环。该图的度序列就是已知数组。
一个非负数组如果是某简单图的度序列,我们称它为可图序列(graphic sequence),简称图序列。
关于图序列,主要研究3个问题:
(1) 存在问题:什么样的整数组是图序列?
(2) 计数问题:一个图序列对应多少不同构的图?
(3) 构造问题:如何画出图序列对应的所有不同构图?
研究现状: (1)彻底解决了,(2)解决得不完整,(3)没有解决。
定理(Havel 1955, Hakimi 1962):非负整数组
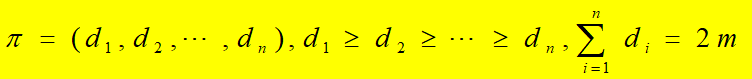
是图序列的充分必要条件是:
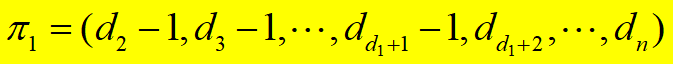 是图序列。
是图序列。
例5  是否为图序列?如果是,作出对应的一个简单图。
是否为图序列?如果是,作出对应的一个简单图。


3、图的频序列及其性质
定理: 一个简单图G的n个点的度不能互不相同
证明: 因为图G为简单图,所以:△(G)≤n-1。
情形1:若G没有孤立点,则 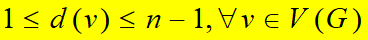
由鸽笼原理:必有两顶点度数相同;
情形2:若G只有一个孤立点,设G1表示G去掉孤立点后的部分,则: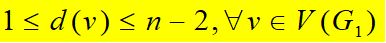
由鸽笼原理:在G1里必有两顶点度数相同;
情形3:若G只有两个以上的孤立点,则定理显然成立。
定义: 设n阶图G的各点的度取s个不同的非负整数d1,d2,…, ds。又设度为di的点有bi个 (i = 1,2,…,s),则 故非整数组(b1,b2,…, bs)是n的一个划分,称为G的频序列。
故非整数组(b1,b2,…, bs)是n的一个划分,称为G的频序列。
定理: 一个n阶图G和它的补图有相同的频序列。





【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 理解Rust引用及其生命周期标识(上)
· 浏览器原生「磁吸」效果!Anchor Positioning 锚点定位神器解析
· 没有源码,如何修改代码逻辑?
· 一个奇形怪状的面试题:Bean中的CHM要不要加volatile?
· [.NET]调用本地 Deepseek 模型
· .NET 10 首个预览版发布,跨平台开发与性能全面提升
· 全程使用 AI 从 0 到 1 写了个小工具
· 快收藏!一个技巧从此不再搞混缓存穿透和缓存击穿
· AI 插件第二弹,更强更好用
· Blazor Hybrid适配到HarmonyOS系统