c语言数据结构复习
c语言数据结构复习
第1章:基本概念
第2章:线性结构
2.1--线性表及其实现
2.1.1-引子:多项式及其表示
法1:顺序存储直接表示多项式

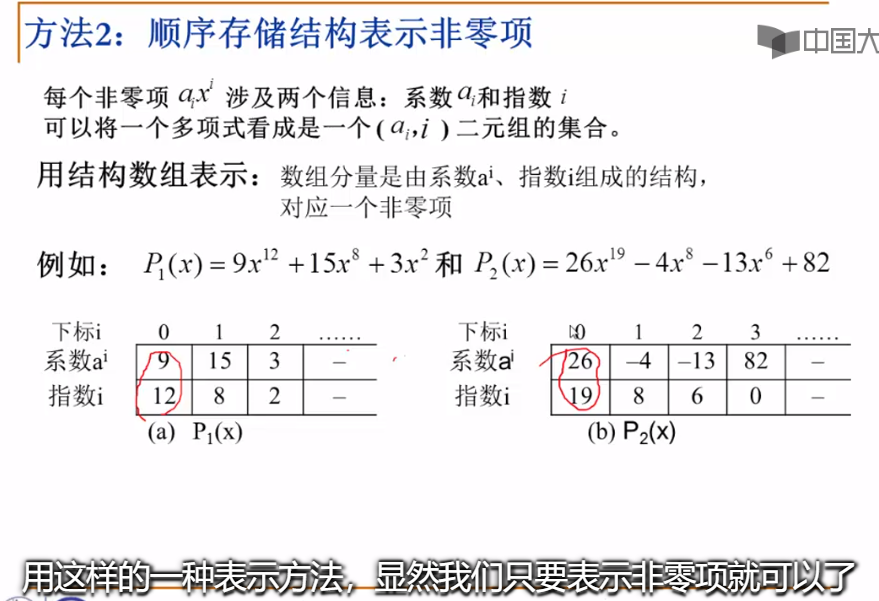
法2:用顺序存储结构表示多项式

说明:
以上例子是表示P1和P2两个多项式相加,先对两个多项式中的指数进行比较,建立一个新数组用于存储指数较大的那个项,直到将两个多项式中的所有项按降序存入第3个数组,其中指数相等的对应系数相加即可
方法3:链表结构表示非零项


2.1.2--线性表及顺序存储-2.1.3-顺序存储的插入与删除
线性表的定义:

线性表的操作:

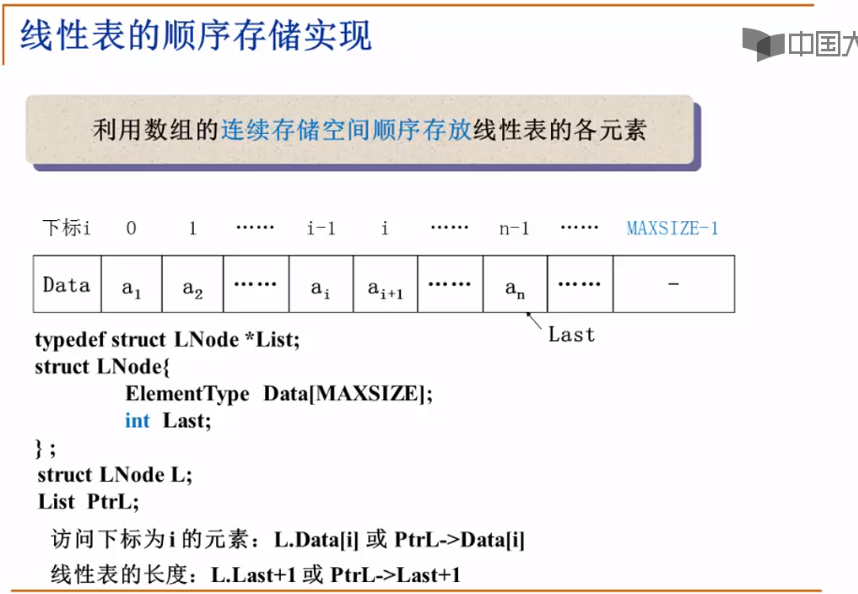
线性表的顺序存储的实现(数组实现):
代码分析:



代码实现:
#include <stdio.h>
#include <malloc.h>
/*采用数组模拟线性表*/
#define MAXSIZE 20
typedef struct LNode * List;//定义一个指向LNode结构的指针
struct LNode{
int Data[MAXSIZE];//创建一个int类型的数组
int Last;//指向数组最后一个元素的下标,最后一个元素并不代表该数组最后一个位置
};
//struct LNode L;
List Ptrl;//定义一个指向该指针结构体的变量
//建立空的顺序表
List MakeEmpty(){
List Ptrl;//定义一个指向该指针结构体的变量
Ptrl = (List)malloc(sizeof(struct LNode));//为结构体类型分配一块内存
Ptrl->Last = -1;//如果该链表没有元素,就将-指向数组最后一个元素的下标Last指向-1,代表空
return Ptrl;
}
//在链表中查找一个元素
int Find(int x, List Ptrl) {//在链表Ptrl中查找一个x
int i = 0;
while(i <= Ptrl->Last && Ptrl->Data[i] != x)
i++;
if (i > Ptrl->Last)
return -1;//如果下标大于最后一个元素的下标,说明该线性表中并没有该元素,返回-1
else
return i;//找到x元素所对应的下标
}
//插入
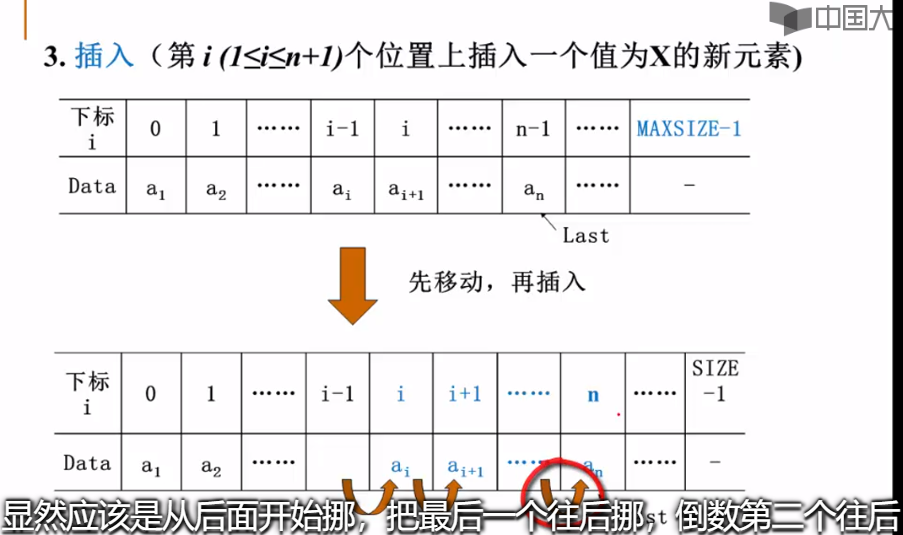
//前提条件:第i(1 <= i <= n+1)个位置上插入一个值为X的新元素,第i个位置也就是i - 1
void Insert(int x,int i,List Ptrl) {//7,11,Ptrl
int j;
if(Ptrl->Last == MAXSIZE-1) {//指向最后一个元素的下标Last指向了MAXSIZE-1,说明数组满
printf("表满");
return;
}
if(i < 1 || i > Ptrl->Last+2) {
/*
*****
插入位置的合法性之说明(2021年11月9日):
i < 1:因为时模拟数组实现的插入,i可以取等于1,也就是可以在下标1-1 = 0处插入元素,也就是说将元素插在顺序表的头部,原先头部元素往后移一个
i > Ptrl->Last+2:
因为第一个if条件已经说明该链表尾部至少还有一个空位,
考虑只剩一个空位的情况:
能够在(Ptrl->last+1)的位置上还插入一个元素,而Ptrl->last+1位置对应的是第Ptrl->last+2的位置
*/
printf("位置不合法");
return;
}
for (j = Ptrl->Last; j >= i-1;j--) {//将下标指向Last
Ptrl->Data[j+1] = Ptrl->Data[j];//将元素从后面移一个位置,从最后一个元素开始,从而将Data[i-1]对应位置空出来
}
Ptrl->Data[i-1] = x;
Ptrl->Last++;//仍然将Last指向最后一个元素
}
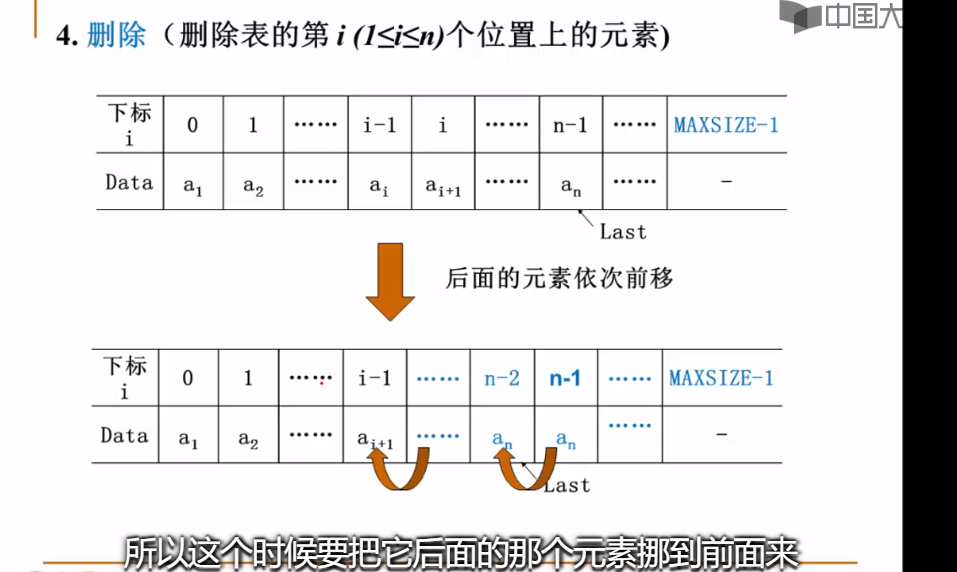
//删除操作的实现,删除第i个元素,也就是删除i-1下标所对应的元素
void Delete(int i, List Ptrl) {
int j;
if(i < 1 || i >Ptrl->Last + 1) {//检查删除位置的合法性
printf("不存在第%d个元素",i);
}
for (j = i; j <= Ptrl->Last; j++) {
Ptrl->Data[j-1] = Ptrl->Data[j];//与插入不同,该操作是将元素从需要插入的位置逐个往前移
}
Ptrl->Last--;
}
int main(void) {
//建立顺序表
Ptrl = MakeEmpty();
//插入--第i(1 <= i <= n+1)个位置上插入一个值为X的新元素,第i个位置也就是i - 1
Insert(1,1,Ptrl);//注意:每一次插入,Ptrl->Last都往后移一位
Insert(2,2,Ptrl);
Insert(3,3,Ptrl);
Insert(4,4,Ptrl);
//查找链表中所有元素
printf("%d\n",Find(1,Ptrl));
printf("%d\n",Find(2,Ptrl));
printf("%d\n",Find(3,Ptrl));
printf("%d\n",Find(4,Ptrl));
//删除操作的实现
Delete(2,Ptrl);
printf("删除元素2后,看一下元素2的状态为:%d\n",Find(2,Ptrl));
printf("删除元素2后,查看3所处的位置为:%d\n",Find(3,Ptrl));
printf("Delete报错测试为:\n");
Delete(0,Ptrl);
printf("\nInsert报错测试为:\n");
Insert(7,4,Ptrl);
/*
按照道理,由于只删除了第2个元素,因为第0个元素不存在,那么Ptrl->Last=2指向了第3个元素,
由Insert()函数中if条件 i > Ptrl->Last+2,4 < Ptrl->Last=3 + 2 == 5,不满足该条件,那么
就可以继续以下操作,插入元素,但是,实际上并没有插入,因位 Delete(0,Ptrl);语句执行了
函数中的Ptrl->Last--; 尽管没有第0个元素,实际上Ptrl->Last=1指向了第2个元素,以下输出将验证
Ptrl->Last的数值
*/
printf("\n验证Ptrl->Last所处的位置为:%d\n",Ptrl->Last);
return 0;
}
结果:
0
1
2
3
删除元素2后,看一下元素2的状态为:-1
删除元素2后,查看3所处的位置为:1
Delete报错测试为:
不存在第0个元素
Insert报错测试为:
位置不合法
验证Ptrl->Last所处的位置为:1
--------------------------------
Process exited after 0.01702 seconds with return value 0
请按任意键继续. . .
2.1.4-链式存储及查找-2.1.5-链式存储的插入与删除
线性表的链式存储实现:
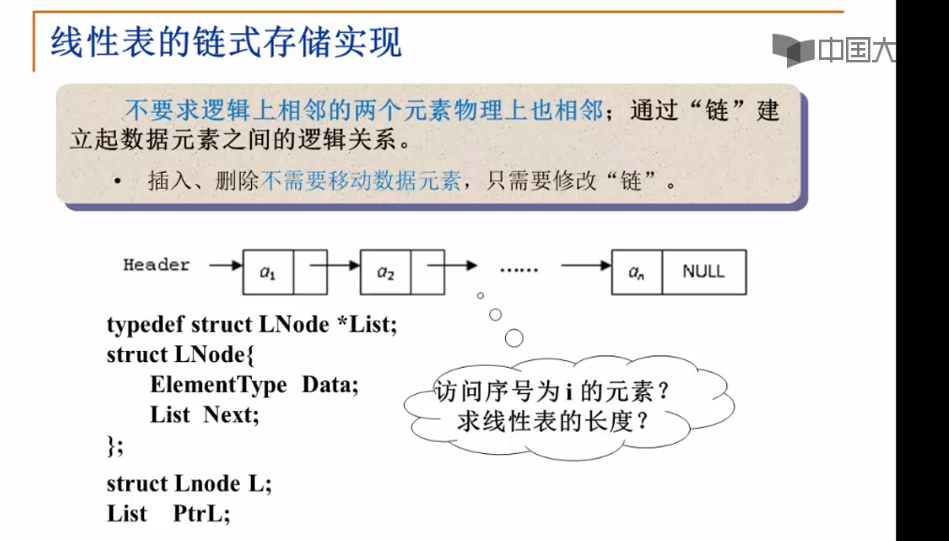
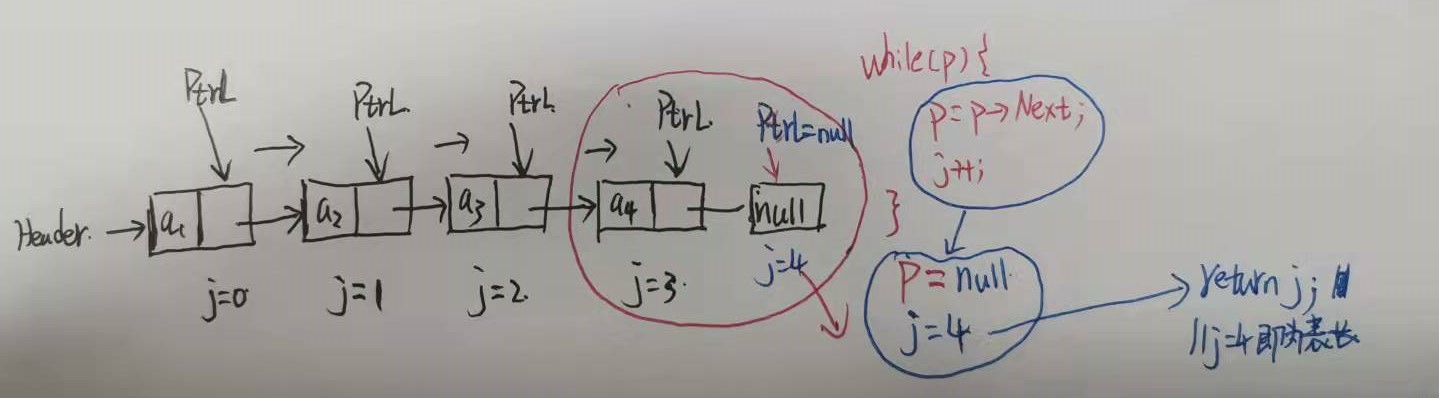
遍历链表求出其表长:

查找:
--注意:PtrL是指向表头,即指向链表的第一个表,也就是指向链表的第一个元素,所以i=1
其中有两种查找方法--按序查找,按值查找:

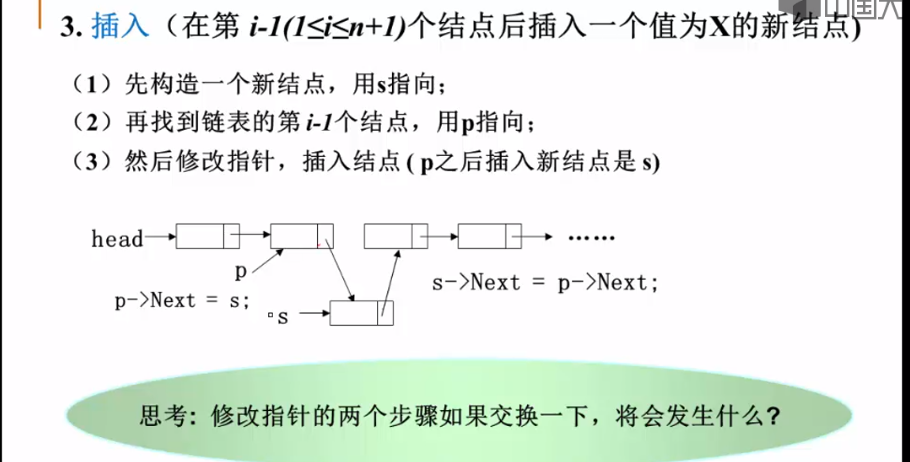
插入:

删除:
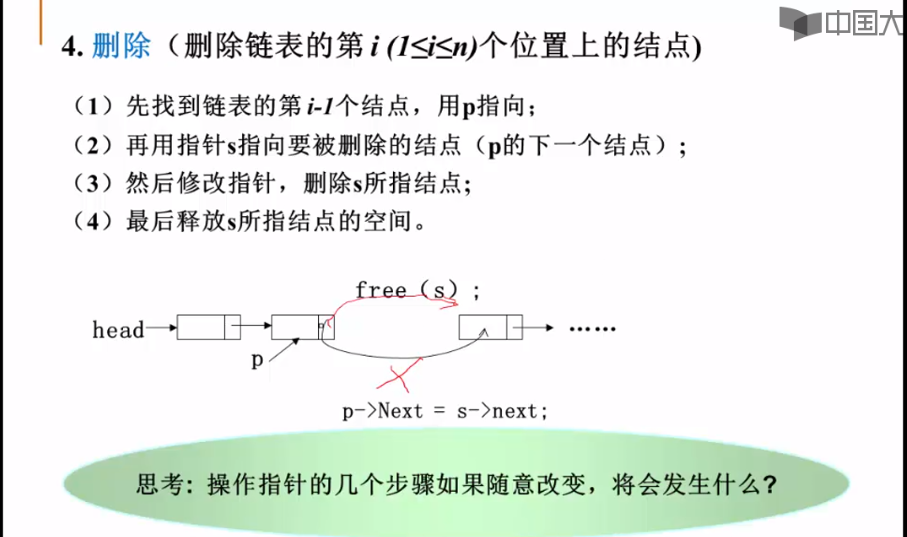
说明:不能简单的删除,因为被删除的节点在创建之初是占用内存的,需要释放----同样创建一个指针s指向被删除节点,然后修改指针进行删除操作,最后释放s所指向的节点的空间

线性表的链式存储实现(浙):
#include <stdio.h>
#include <malloc.h>
typedef struct LNode *List;
struct LNode {
int Data;
List Next;
};
List PtrL;//创建指向空的结点
//函数声明
int Length(List PtrL);
List Find(int x,List Ptrl);
List FindKth(int K, List Ptrl);
List Insert(int x,int i,List PtrL);
List Delect(int i, List PtrL);
int main() {
PtrL = Insert(1,1,PtrL);
Insert(2,2,PtrL);
Insert(3,3,PtrL);
Insert(4,4,PtrL);
Insert(5,5,PtrL);
// PtrL = Insert(1,1,PtrL);
// Insert(2,1,PtrL);
// Insert(3,1,PtrL);
// Insert(4,1,PtrL);
// Insert(5,1,PtrL);
//写一个for循环将链表显示出来
List temp;
temp = PtrL;
for(int i = 1; i <= Length(PtrL); i++) {
printf("第%d个结点的Data = %d\n",i,temp->Data);
temp = temp->Next;
}
return 0;
}
//遍历链表求出其表长
int Length(List PtrL) {
List p = PtrL;
int j = 0;
while(p) {
p = p->Next;
j++;
}
return j;
}
//在链表中查找某一个元素
//此处采用按值查找
List Find(int x,List Ptrl) {
List p = Ptrl;//设立一个临时指针指向该链表的头节点
while (p != NULL && p->Data != x) {
p = p->Next;
}
return p;
}
//按序号查找
List FindKth(int K, List Ptrl) {//K代表第K个元素
List p = Ptrl;
int i = 1;//注意:PtrL是指向表头,即指向链表的第一个表,也就是指向链表的第一个元素,所以i=1
while(p != NULL && i < K) {
p = p->Next;
i++;
}
if (i == K) {
return p;
} else {
return NULL;
}
}
//插入--在第i-1个节点后插入一个值为x的新节点
/*此插入方法有一个缺点:在main方法中注释可见,对于该种特殊插入(多次从头部插入)只会在第一次插入插入成功--
原因:该方法没有对头部结点做好的处理,对于该种特殊方法,每次返回的都是头部结点,而每次调用Insert(3,1,PtrL);
其中的参数Ptrl就是指向该头部节点的指针,但是当第2次插入以后,没有进行PtrL = Insert(2,1,PtrL);该操作,也就是
没有对其进行头部结点PtrL的更新,头部还是指向插入的第一个元素,那么自然无法进行插入操作,解决办法如下(或者采用
浙大老师的另一种设计插入的方法) :更新头部PtrL就行了
PtrL = Insert(1,1,PtrL);
PtrL = Insert(2,1,PtrL);
PtrL = Insert(3,1,PtrL);
PtrL = Insert(4,1,PtrL);
PtrL = Insert(5,1,PtrL);
*/
List Insert(int x,int i,List PtrL) {//也就是说在第i个节点之处插入该新节点
List p,s;
if(i == 1) {
s=(List)malloc(sizeof(struct LNode));//为新节点开辟一块内存
s->Data = x;//把待插入的值赋值给该新节点结构体中的变量Data
s->Next = PtrL;//因为i等于1,也就是说在第一个节点处插入该节点,也就是说该新插入的节点想变成头节点
return s;
}
p = FindKth(i-1,PtrL);//找到待插入节点的上一个节点
if(p == NULL) {//第i-1个节点不存在,不能插入
printf("参数i错");
return NULL;
}else {
s = (List)malloc(sizeof(struct LNode));//申请,填装节点
s->Data = x;
s->Next = p->Next;
p->Next = s;
return PtrL;
}
}
//删除第i个结点
List Delect(int i, List PtrL) {
List p,s;
if(i == 1) {
s = PtrL;//将s结点指向头结点,便于后面释放内存操作
if (PtrL != NULL) {
PtrL = PtrL->Next;
} else {
return NULL;
}
free(s);
return PtrL;
}
p = FindKth(i-1, PtrL);//找到待删除结点的上一个结点
if(p == NULL) {
printf("第%d个结点不存在",i-1);
return NULL;
} else if (p->Next == NULL) {
printf("第%d个结点不存在",i);
return NULL;
} else {
s = p->Next;
p->Next = s->Next;
free(s);
return PtrL;
}
}
结果:
第1个结点的Data = 1
第2个结点的Data = 2
第3个结点的Data = 3
第4个结点的Data = 4
第5个结点的Data = 5
--------------------------------
Process exited after 0.05752 seconds with return value 0
请按任意键继续. . .
2.1.6--广义表与多重链表
1.广义表的定义
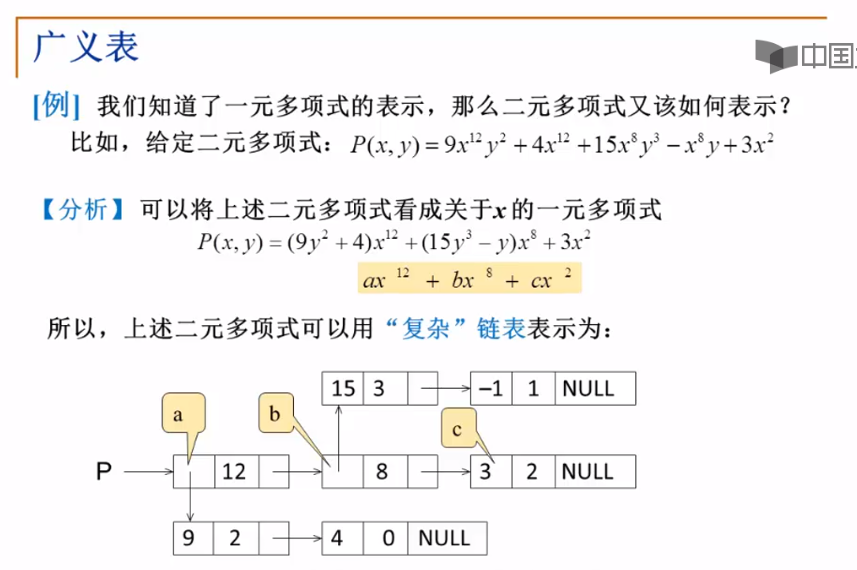

2.多重链表

双向链表是一个节点中有两个指针域,但他所连接起来的还是一个链表,所以说并非多重链表
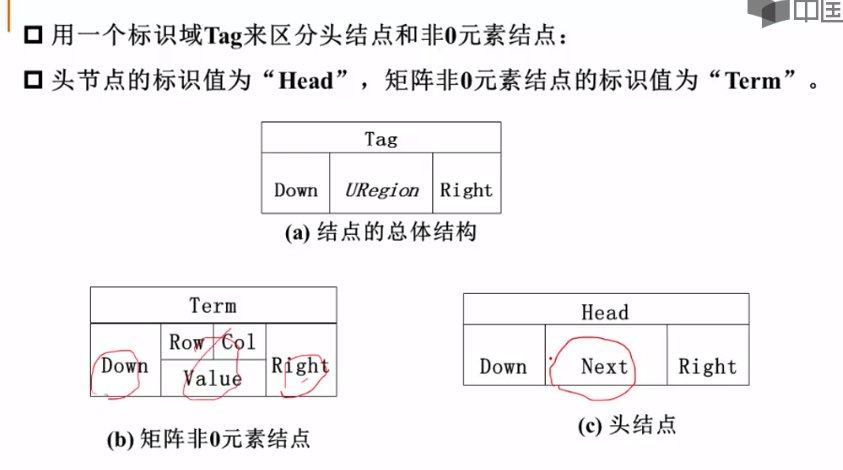
十字链表的概念:
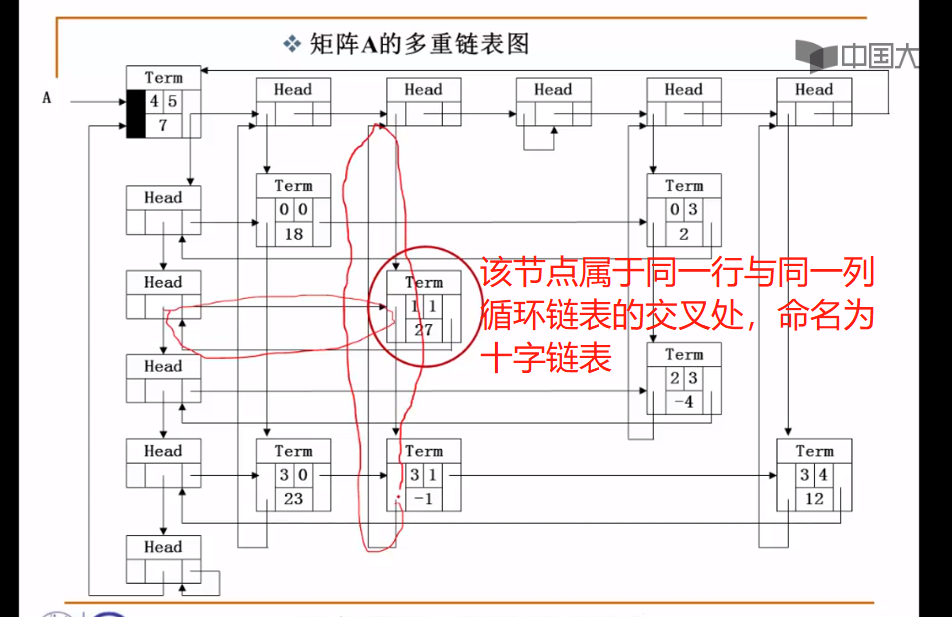
Head节点与Term节点的解释:
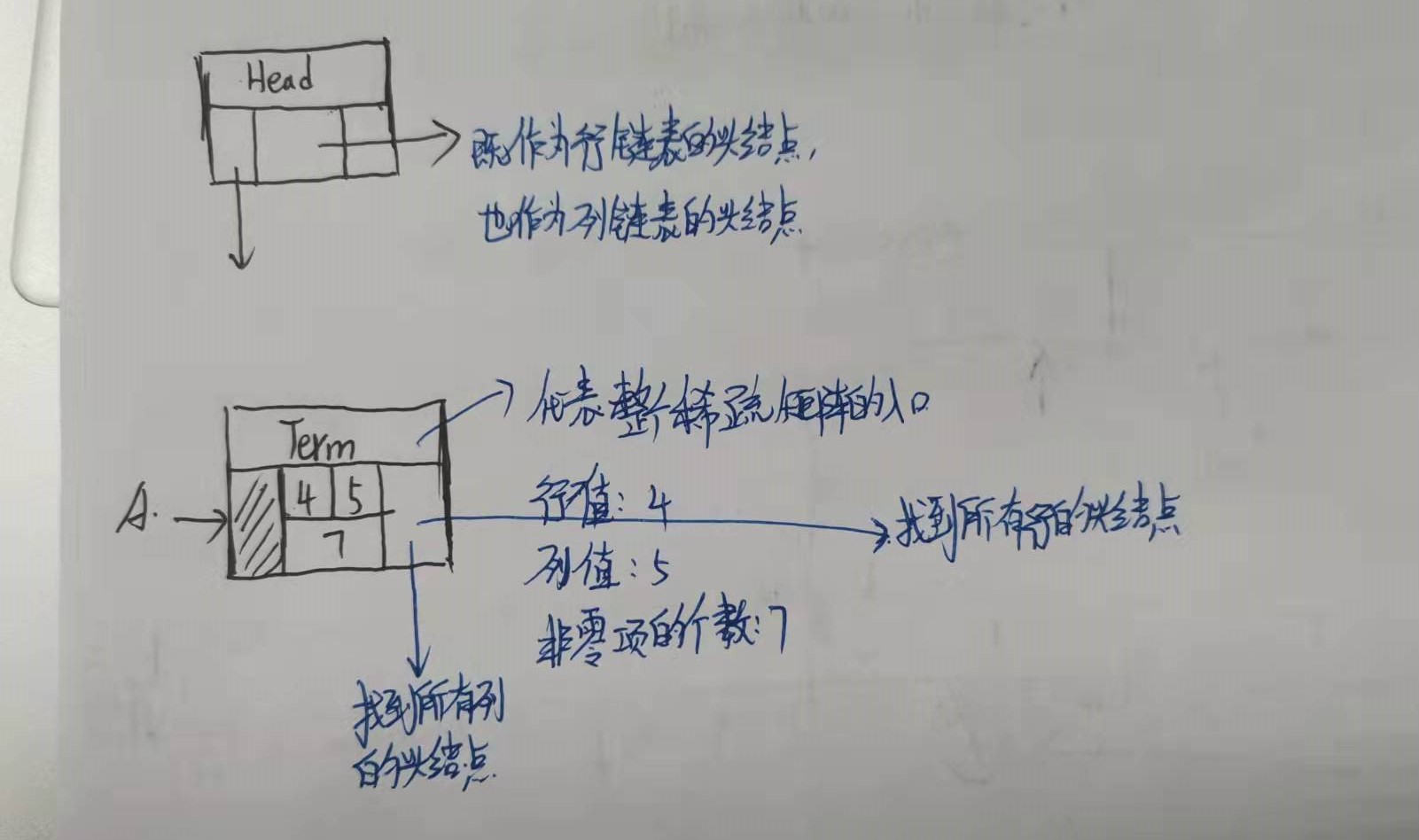
节点实现分析:
2.2-堆栈
2.2.1-堆栈的概念
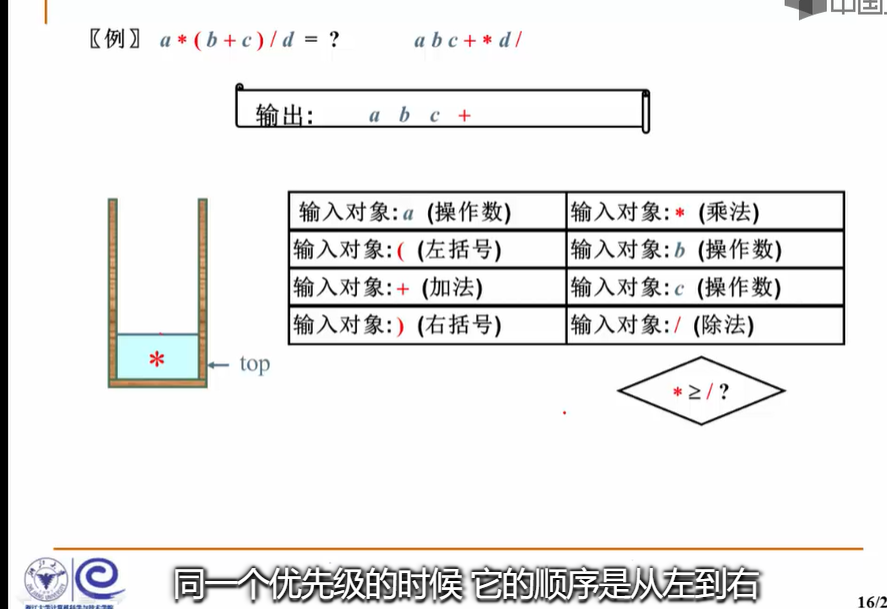
一个例子--表达式求值


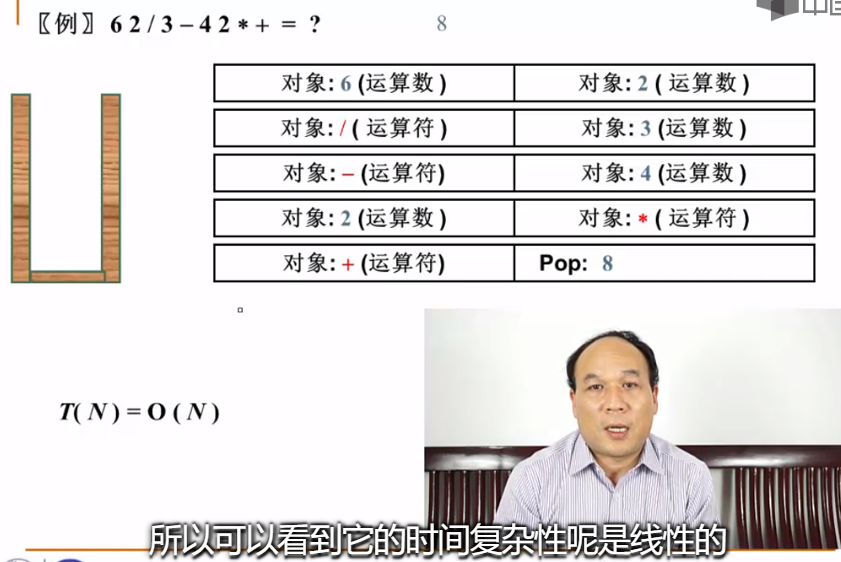
堆栈的抽象类型描述:


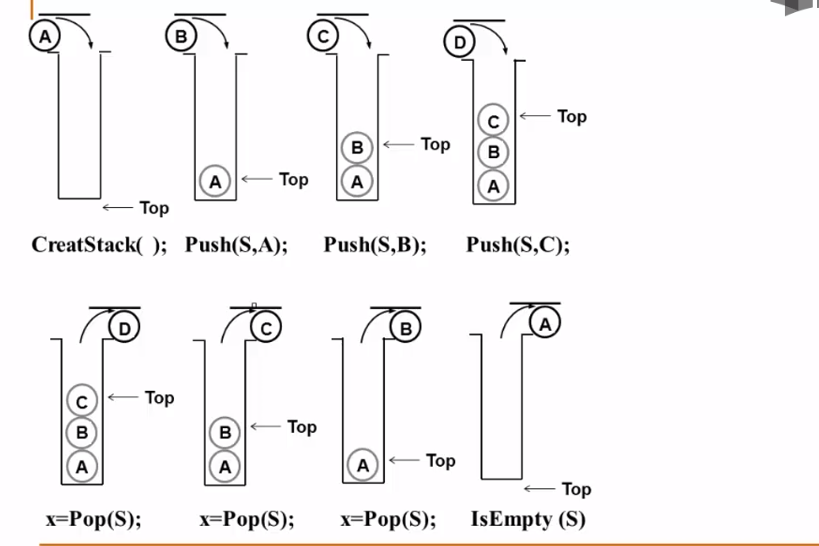
实例:

2.2.2--栈的顺序实现
1.代码实现分析:
1.入栈分析
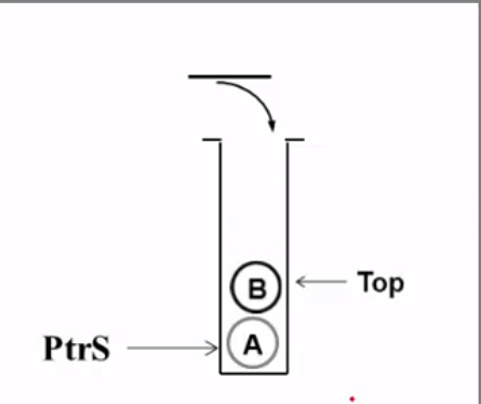
top是一个int类型,其指向数组下标,当数组为空时,Top=-1,当希望向堆栈中存入数据时,先将Top加1,然后向该下标处存入一个数据

2.出栈分析:
先将元素出栈,然后将Top减1

2.用一个数组实现两个堆栈

push操作:

pop操作:

栈的顺序存储实现----用一个数组实现两个堆栈:
#include <stdio.h>
#include <malloc.h>
#include <stdbool.h>
#define MaxSizeArray 16//该程序的缺陷之处:调用CreateStack(int MaxSize)函数时,需与MaxSize保持一致(重在理解堆栈,哈哈)
//用一个数组实现两个堆栈
typedef struct DStack *Stack;
typedef int Position;
struct DStack {
int *Data;//存储元素的数组
Position Top1;//堆栈1的顶部指针
Position Top2;//堆栈2的顶部指针,也可以说是堆栈的最大容量
};
//创建一个空的堆栈
Stack CreateStack(int MaxSize) {
//为所创造的DStack栈分配内存
Stack S = (Stack)malloc(sizeof(struct DStack));
//为数组分配内存
S->Data = (int *)malloc(MaxSize * sizeof(int));
S->Top1 = -1;
S->Top2 = MaxSize;
return S;
}
//判断栈是否为空
bool IsEmpty(Stack PtrS) {
return PtrS->Top1 == -1;
}
//判断栈是否m
bool IsFull(Stack PtrS) {
return PtrS->Top2 - PtrS->Top1 == 1;
}
//push操作
void Push(Stack PtrS, int item, int Tag) {
if(IsFull(PtrS)) {
printf("堆栈满");
return;
}
if (Tag == 1) //对第一个栈进行操作
PtrS->Data[++(PtrS->Top1)] = item;
else//对第二个栈进行操作
PtrS->Data[--(PtrS->Top2)] = item;
}
//pop操作
int Pop(Stack PtrS,int Tag) {
if (Tag == 1) {//对同一个数组中的其中一个堆栈1进行操作
if(IsEmpty(PtrS)) {
printf("堆栈1空");
return NULL;
} else {
return PtrS->Data[(PtrS->Top1)--];
}
} else {
if(PtrS->Top2 == MaxSizeArray) {//对同一个数组中的其中一个堆栈2进行操作
printf("堆栈2空");
return NULL;
} else {
return PtrS->Data[(PtrS->Top2)++];
}
}
}
//编写一个测试函数
/*
明确:函数返回值是void,函数参数设置:堆栈S,以及其所对应的哪一个堆栈tag
设置一个int类型的临时变量temp指向top1 or to2
利用for循环对堆栈进行遍历,临界值是temp指向-1,或者MaxSize
*/
void ShowStack(Stack S,int tag) {
Position temp;
if(tag == 1) {
temp = S->Top1;
for(int i = temp; i >= 0; i--) {
printf("下标为%d的值为:%d\n",i,S->Data[i]);
}
} else {
temp = S->Top2;
for(int i = temp; i < MaxSizeArray; i++) {
printf("下标为%d的值为:%d\n",i,S->Data[i]);
}
}
}
int main(void) {
Stack S = CreateStack(16);
//对堆栈1进行操作
Push(S,1,1);
Push(S,2,1);
Push(S,3,1);
Push(S,4,1);
//对堆栈2进行操作
Push(S,16,2);
Push(S,15,2);
Push(S,14,2);
Push(S,13,2);
// StackTest(Stack S,int tag)---显示堆栈
//push--test
printf("pop--test");
printf("堆栈1为:\n");
ShowStack(S,1);
printf("\n堆栈2为:\n");
ShowStack(S,2);
//pop--test
printf("\npop--test\n");
Pop(S,1);//将下标为3所在元素Pop出去
ShowStack(S,1);
Pop(S,1);//将下标为2所在元素Pop出去
Pop(S,1);//将下标为1所在元素Pop出去
printf("\n只剩一个元素,将其显示\n");
ShowStack(S,1);
Pop(S,1);//将下标为0所在元素Pop出去
ShowStack(S,1);
printf("\n报堆栈1空的提示\n");
Pop(S,1);//堆栈1中没有元素,报--堆栈1空--的提示
return 0;
}
结果:
pop--test堆栈1为:
下标为3的值为:4
下标为2的值为:3
下标为1的值为:2
下标为0的值为:1
堆栈2为:
下标为12的值为:13
下标为13的值为:14
下标为14的值为:15
下标为15的值为:16
pop--test
下标为2的值为:3
下标为1的值为:2
下标为0的值为:1
只剩一个元素,将其显示
下标为0的值为:1
报堆栈1空的提示
堆栈1空
--------------------------------
Process exited after 0.0282 seconds with return value 0
请按任意键继续. . .
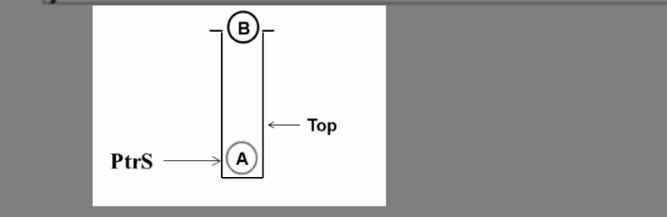
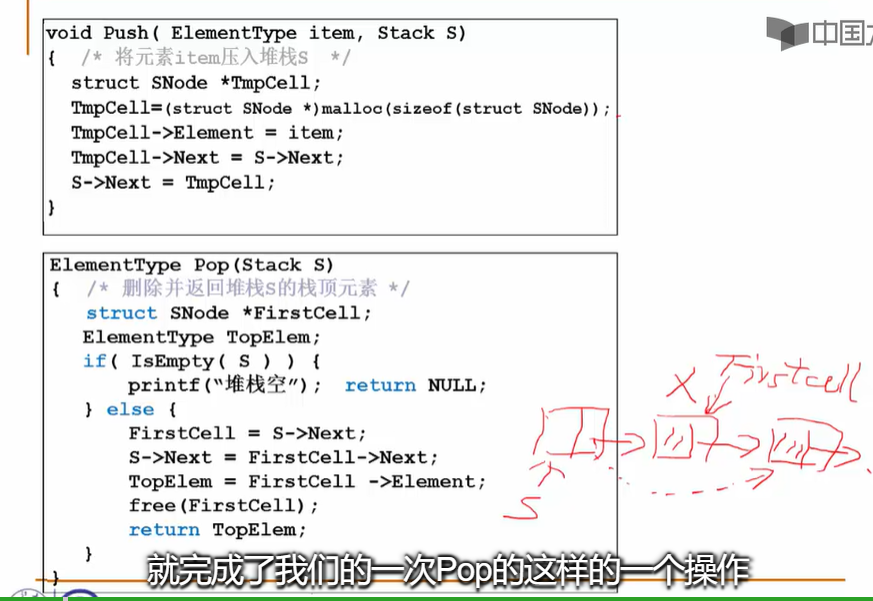
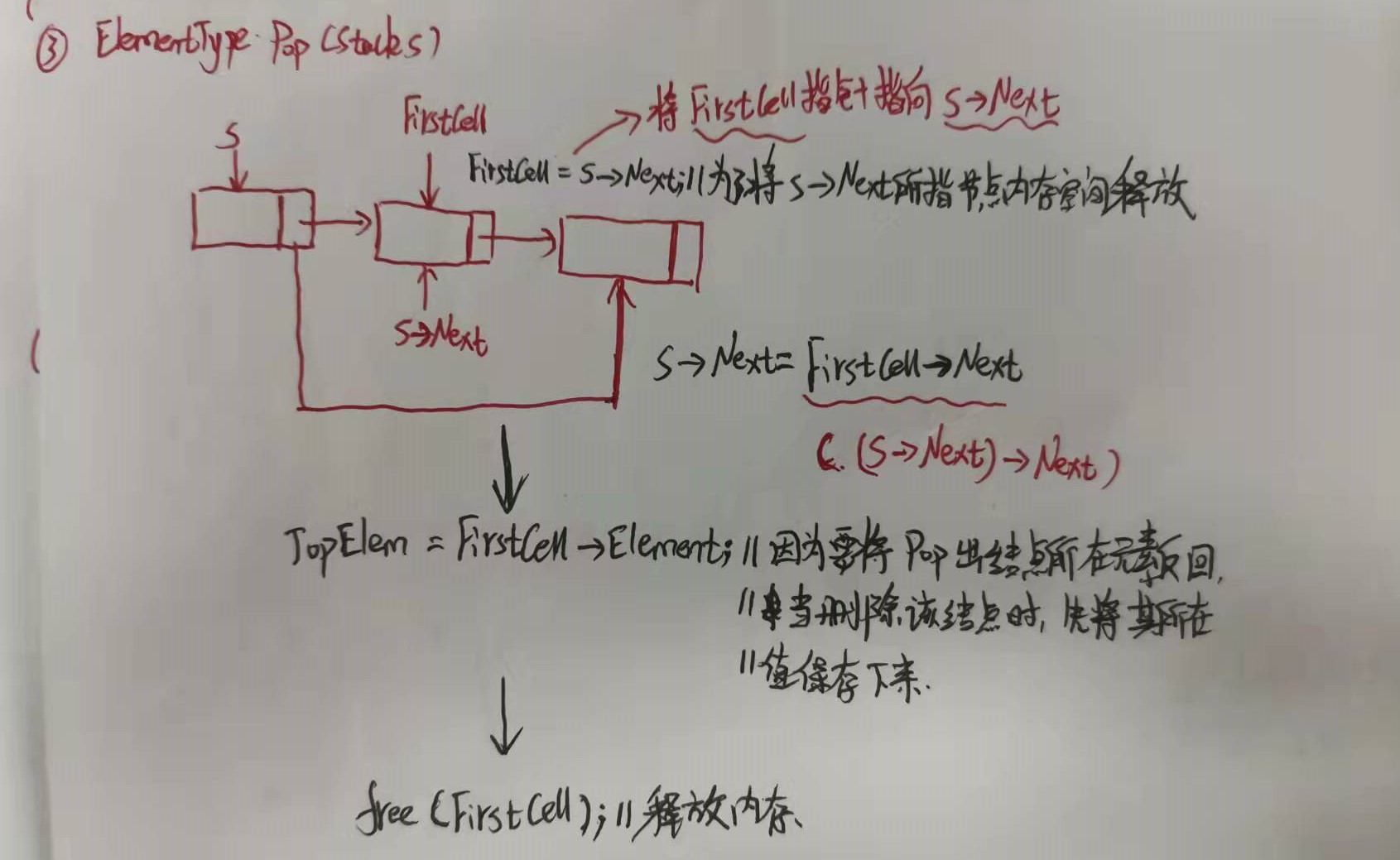
2.2.3-堆栈的链式存储实现
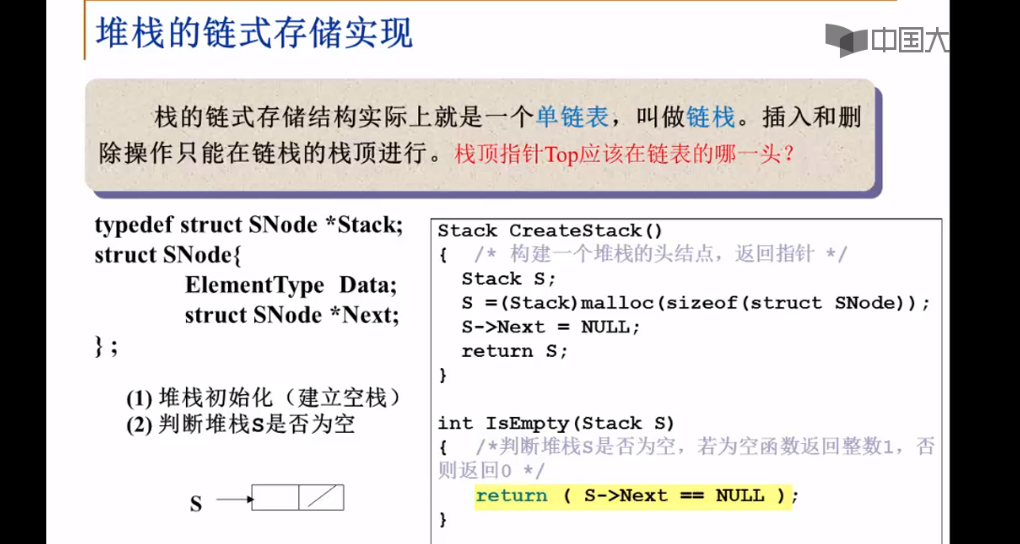
1.不能将栈顶指针Top指向链式尾部之说明:


2.将栈顶指针Top指向链表尾部之分析:

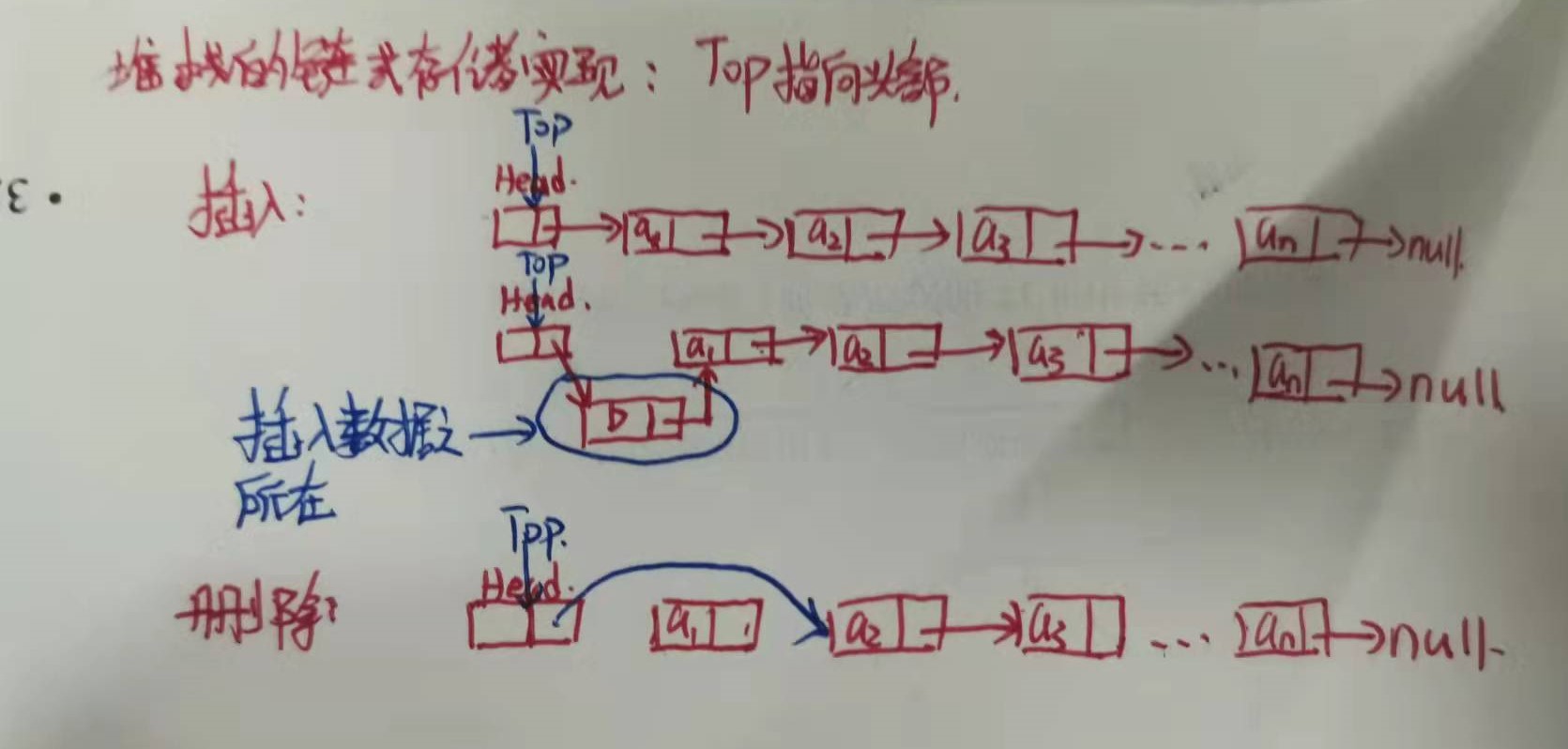
3.代码实现

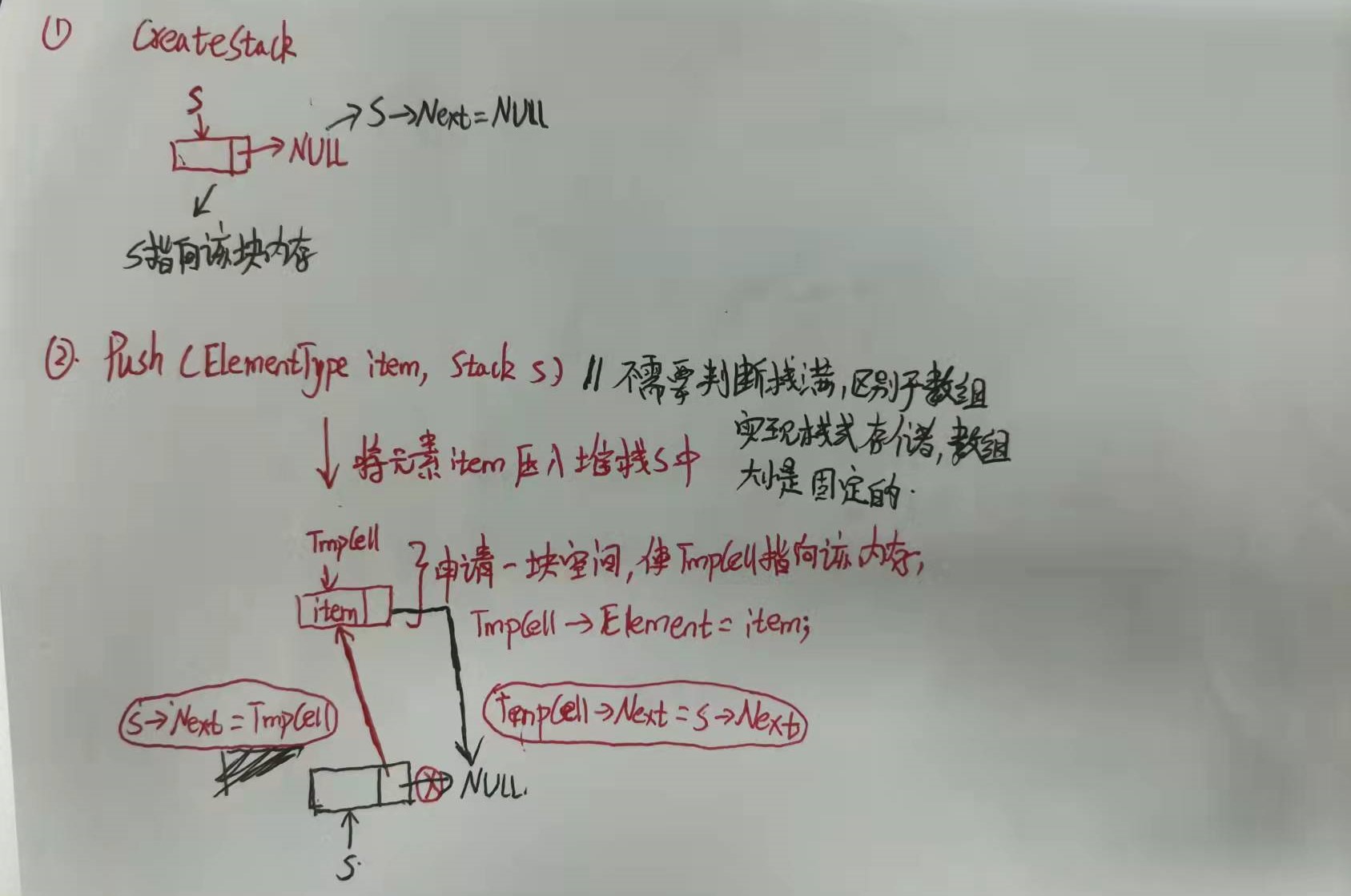
2.2.4----中缀表达式转后缀表达式----堆栈的应用--表达式求值



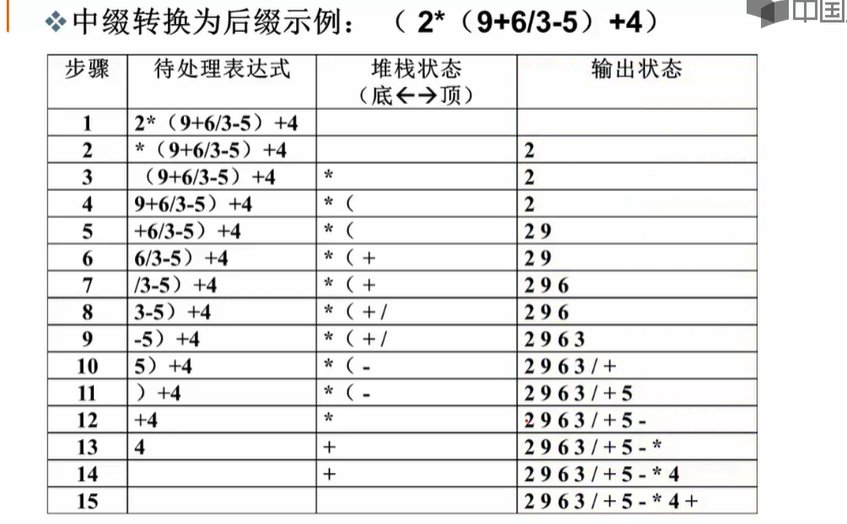

2.3-队列
2.3.1-队列以及顺序存储实现
1.队列的定义:
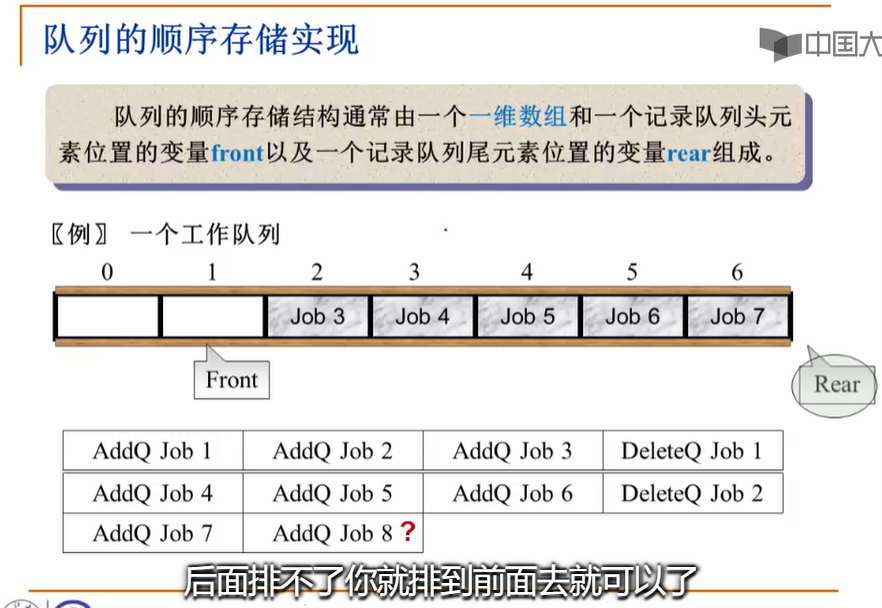



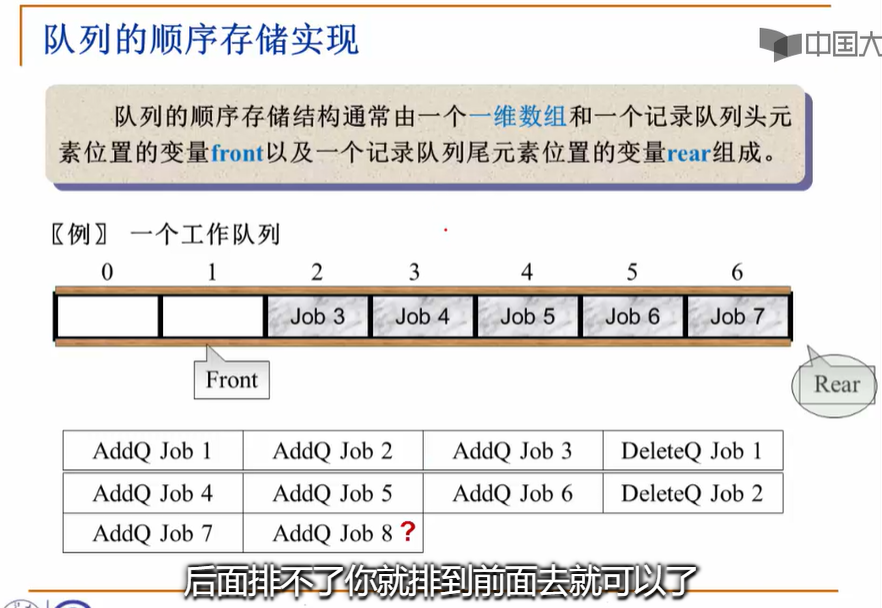

2.循环队列:
2-1 为什么要留一个空位:
不留一个空位,当rear==front时,无法判断该队列是空还是满
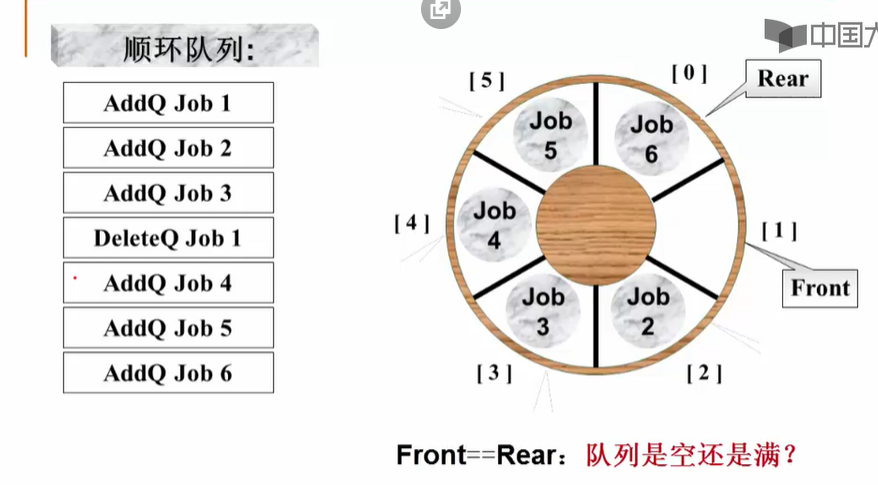
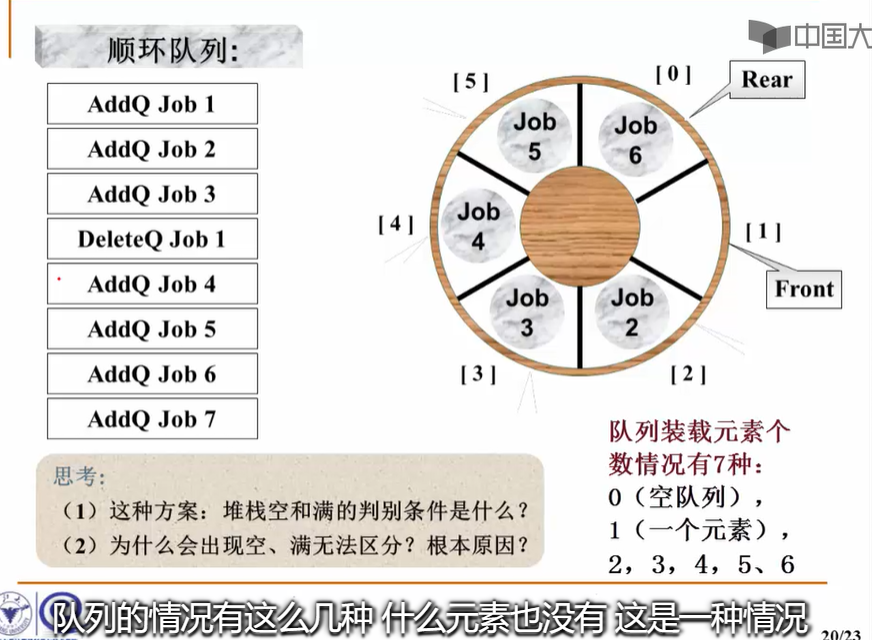

2-2 代码实现分析:

3.c语言队列的顺序存储实现
#include <stdio.h>
#include <malloc.h>
#include <stdbool.h>
//队列的顺序存储实现
typedef int Position;
struct QNode {
int *Data;
Position Front,Rear;//定义队列的头部以及尾部
int MaxSize;//数组的大小
};
typedef struct QNode *Queue;
Queue CreateQueue(int MaxSize) {
Queue Q = (Queue)malloc(sizeof(struct QNode));//为该队列分配一块内存空间
Q->Data = (int *)malloc(MaxSize * sizeof(int));//为数组分配一块内存空间
Q->Front = Q->Rear = 0;
Q->MaxSize = MaxSize;
return Q;
}
bool IsFull(Queue Q) {
/*队列的顺序存储的实现--理解关键之处:(Q->Rear + 1) % Q->MaxSize == Q->Front
该代码采取预留一个空位解决了(Front==Rear)时,对列是满还是空的问题。该公式就实现
了该判断,(注意Front==Rear==0),并且当队列为满时,肯定是队列只剩余一个空位
而Front总是指向该空位。(Front指向的位置一定没有元素,Rear总是指向队列尾部的最后一个元素
*/
return ((Q->Rear + 1) % Q->MaxSize == Q->Front);
}
bool AddQ(Queue Q, int x) {
if (IsFull(Q)) {
printf("队列满");
return false;
} else {
Q->Rear = (Q->Rear + 1) % Q->MaxSize;
Q->Data[Q->Rear] = x;
return true;
}
}
bool IsEmpty(Queue Q) {
return (Q->Front == Q->Rear);
}
int DeleteQ(Queue Q) {
if (IsEmpty(Q)) {
printf("队列空");
// return ERROR;
} else {
Q->Front = (Q->Front+1) % Q->MaxSize;
return Q->Data[Q->Front];
}
}
//定义一个显示队列的方法
void showQueue(Queue Q){
//判断是否为空
if(IsEmpty(Q)) {
printf("队列为空,不能显示数据");
return;
}
//遍历数组,显示数据
/*
(Q->Rear+Q->MaxSize-Q->Front) % Q->MaxSize):
该语句计算出Front与Rear相差多少,加上一个Q->Front,就为i设定了边界值
*/
for (int i = Q->Front + 1; i <= Q->Front + ((Q->Rear+Q->MaxSize-Q->Front) % Q->MaxSize); i++) {
printf("Q->Data[%d] = %d\n",i%Q->MaxSize,Q->Data[i%Q->MaxSize]);//取模运算的奇妙之处
}
}
int main(void) {
Queue Q = CreateQueue(5);
printf("直接显示数据Test:因为预留了一个位置,队列只能增加4个元素(队里数组大小为5):\n");
AddQ(Q,1);
AddQ(Q,2);
AddQ(Q,3);
AddQ(Q,4);
showQueue(Q);
printf("队列满Test:\n");
AddQ(Q,5);
printf("\n元素出队列Test:\n");
printf("出队列值:%d\n",DeleteQ(Q));
printf("出队列值:%d\n",DeleteQ(Q));
printf("出队列值:%d\n",DeleteQ(Q));
printf("出队列值:%d\n",DeleteQ(Q));
printf("\n空队列显示Test:\n");
DeleteQ(Q);
return 0;
}
输出结果:
直接显示数据Test:因为预留了一个位置,队列只能增加4个元素(队里数组大小为5):
Q->Data[1] = 1
Q->Data[2] = 2
Q->Data[3] = 3
Q->Data[4] = 4
队列满Test:
队列满
元素出队列Test:
出队列值:1
出队列值:2
出队列值:3
出队列值:4
空队列显示Test:
队列空
--------------------------------
Process exited after 0.06129 seconds with return value 0
请按任意键继续. . .
2.3.2-队列的链表存储的实现


2.4-应用实例
多项式相加:


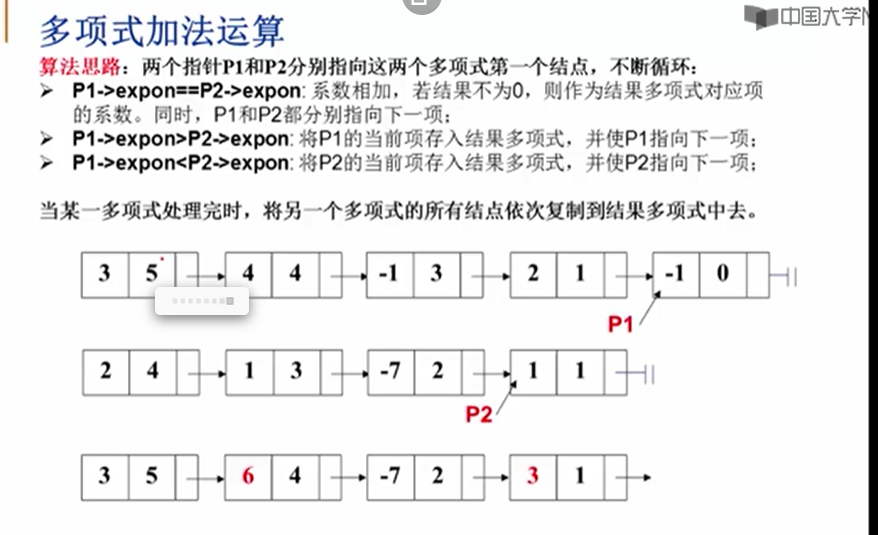
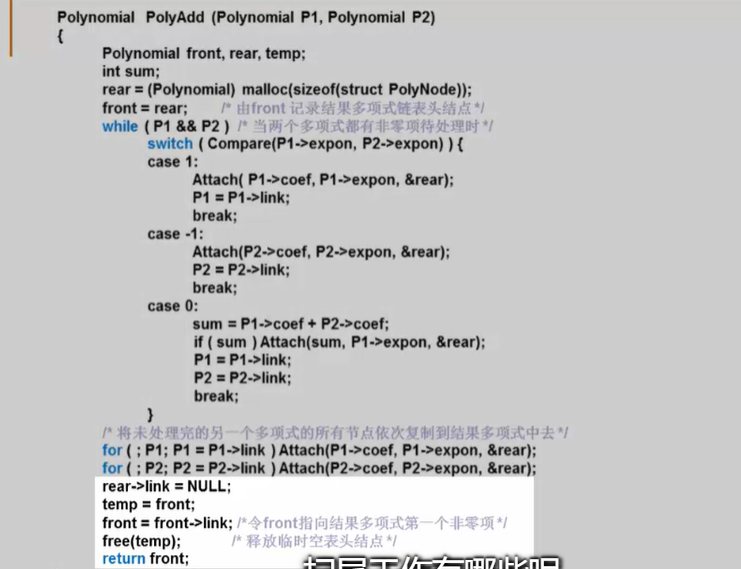
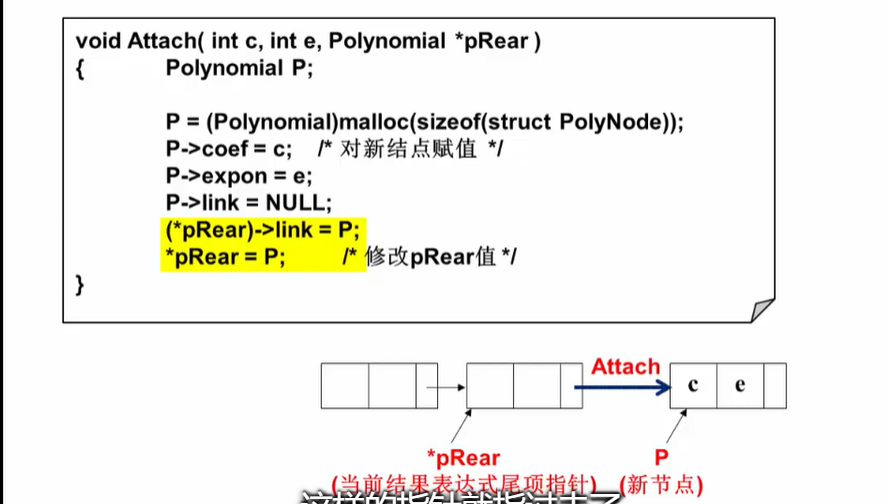
疑问:这里为什么要使用*pRear--指针的指针
自己使用代码实现:
#include <stdio.h>
#include <stdlib.h>
typedef struct Node *PNode;
struct Node
{
int xishu;
int zhishu;
PNode next;
};
/*
**1.创建一个链表
*/
PNode createLinked();
/*
**2.往链表中增添数值
*/
void add(int xishu, int zhishu, PNode Linked);
/*
** 设置一个方法用于展示链表
*/
void showLinked(PNode L);
/*
** 写一个函数用于比较多项式的系数
*/
int compare(int a,int b);
/*
** 用于多项式的合并
*/
PNode polynomialsOfAdd(PNode P1,PNode P2);
int main(int argc, char const *argv[])
{
//创建存储多项式1的链表
PNode P1 = createLinked();
//创建存储多项式2的链表
PNode P2 = createLinked();
//为P1增加多项式中所对应的系数和指数
add(3, 5, P1);
add(4, 4, P1);
add(-1, 3, P1);
add(2, 1, P1);
add(-1, 0, P1);
// showLinked(P1);
//为P2增加多项式中所对应的系数和指数
add(2, 4, P2);
add(1, 3, P2);
add(-7, 2, P2);
add(1, 1, P2);
PNode P3 = polynomialsOfAdd(P1,P2);
showLinked(P3);
// getchar();
return 0;
}
/*
**1.创建一个链表
*/
PNode createLinked()
{
PNode Linked;
Linked = (PNode)malloc(sizeof(struct Node));
Linked->xishu = 0;
Linked->zhishu = 0;
Linked->next = NULL;
return Linked;
}
/*
**2.往链表中增添数值
*/
void add(int xishu, int zhishu, PNode Linked)
{
PNode temp, newNode;
temp = Linked;
//找到最后一个节点
while (temp->next != NULL)
{
temp = temp->next;
}
//创建一个节点,分配内存存储数值
newNode = (PNode)malloc(sizeof(struct Node));
newNode->xishu = xishu;
newNode->zhishu = zhishu;
newNode->next = NULL;
//将节点加到链表中
temp->next = newNode;
}
/*
** 设置一个方法用于展示链表
*/
void showLinked(PNode L)
{
PNode temp;
temp = L->next;
while (temp)
{
printf("系数为:%d;指数为:%d\n", temp->xishu, temp->zhishu);
temp = temp->next;
}
}
/*
** 写一个函数用于比较多项式的系数
*/
int compare(int a,int b) {
if (a > b) {
return 1;
} else if (a < b) {
return -1;
} else {
return 0;
}
}
/*
** 用于多项式的合并
*/
PNode polynomialsOfAdd(PNode P1,PNode P2) {
PNode tempOfP1;
tempOfP1 = P1->next;
PNode tempOfP2;
tempOfP2 = P2->next;
//创建P3链表用于存储合并之后的多项式
PNode P3 = createLinked();
while (tempOfP1 && tempOfP2) {
switch (compare(tempOfP1->zhishu,tempOfP2->zhishu))
{
case 1:
add(tempOfP1->xishu,tempOfP1->zhishu,P3);
tempOfP1 = tempOfP1->next;
break;
case -1:
add(tempOfP2->xishu,tempOfP2->zhishu,P3);
tempOfP2 = tempOfP2->next;
break;
case 0:
//如果系数相加为0,直接舍去,无需加到链表中
if ((tempOfP1->xishu+tempOfP2->xishu) == 0)
{
tempOfP1 = tempOfP1->next;
tempOfP2 = tempOfP2->next;
break;
}
add(tempOfP1->xishu+tempOfP2->xishu,tempOfP1->zhishu,P3);
tempOfP1 = tempOfP1->next;
tempOfP2 = tempOfP2->next;
break;
}
}
while (tempOfP1)
{
add(tempOfP1->xishu,tempOfP1->zhishu,P3);
tempOfP1 = tempOfP1->next;
}
while (tempOfP2)
{
add(tempOfP2->xishu,tempOfP2->zhishu,P3);
tempOfP2 = tempOfP2->next;
break;
}
return P3;
}
结果:
系数为:3;指数为:5
系数为:6;指数为:4
系数为:-7;指数为:2
系数为:3;指数为:1
系数为:-1;指数为:0
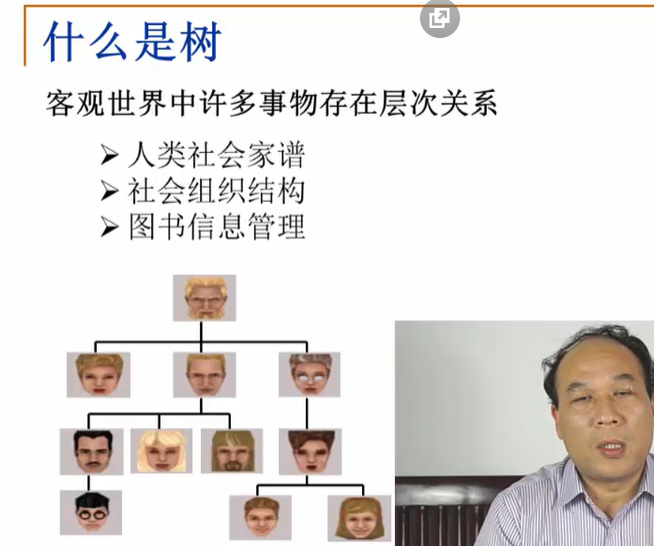
第3章:树
3.1-引子
3.1.1-引子

查找:

哨兵的简单介绍:
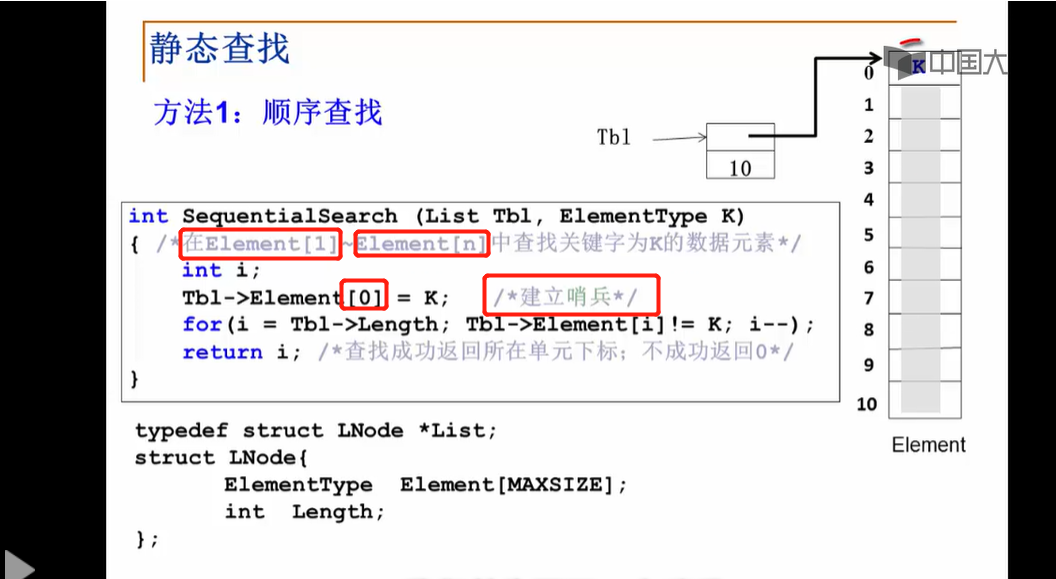
既然是边界所在的位置设置了哨兵,那么遍历的元素只能除开哨兵,如图是从Element[1]~Element[n]之中查找,Element[0]为哨兵值

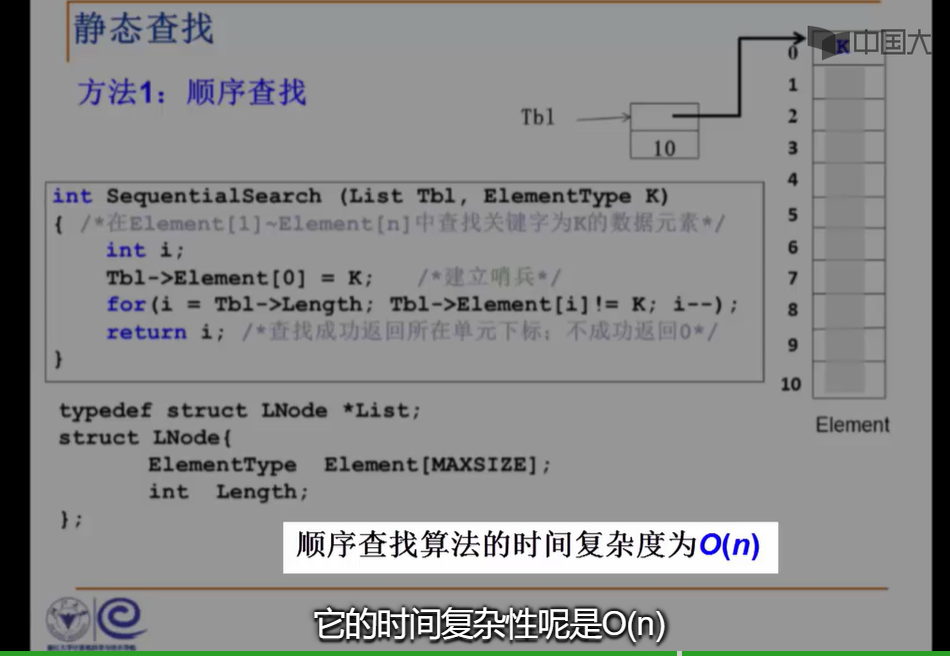
运气好第一个就找到了,运气不好最后一个(n)才找到,平均是n/2
3.1.2--二分查找

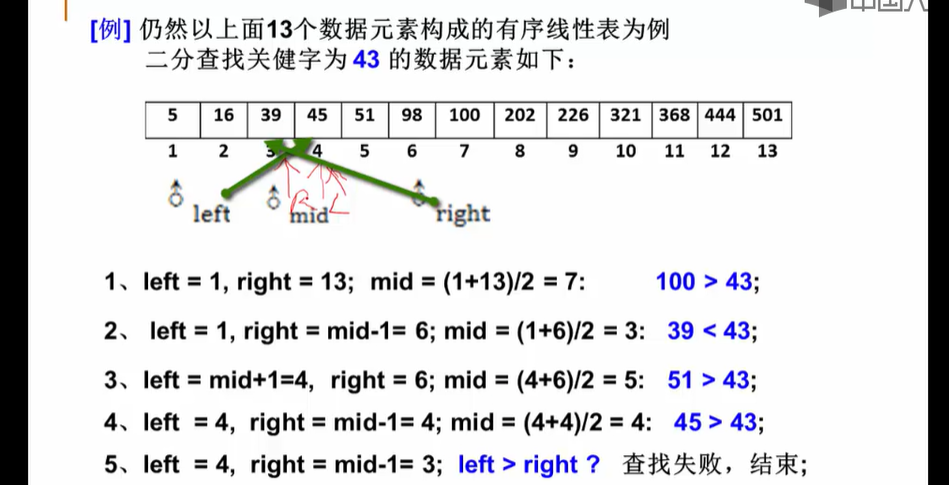
3.1.3--二分查找的实现

2.时间复杂度:

2.11个元素二分查找判定树
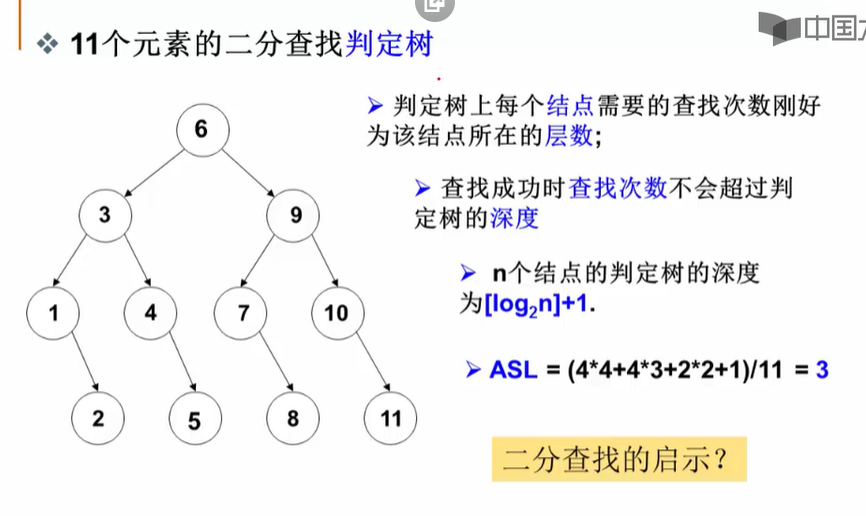
ASL:平均成功查找次数(有问题)
3.二分查找的程序实现中,如果left和right的更新不是取mid+1和mid-1而是都取mid

3.1.4-树的定义
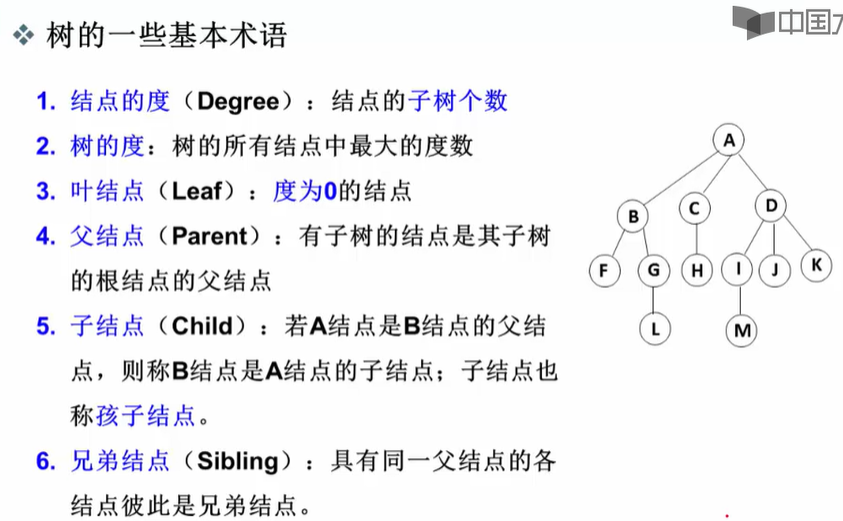
1.定义:
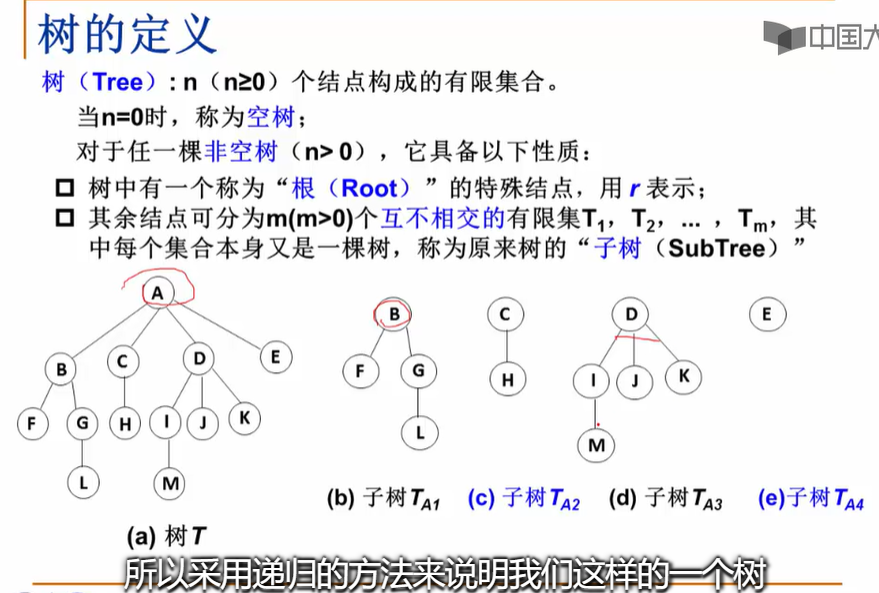
2.树的一些基本术语