3.给定一个整数序列，求其中整数加起来最大子序列和（因为该数列中可能有负数）-穷举法，分治法

3.给定一个整数序列，求其中整数加起来最大子序列和（因为该数列中可能有负数）-分治法

参考文献：编程珠玑第八章-分治算法

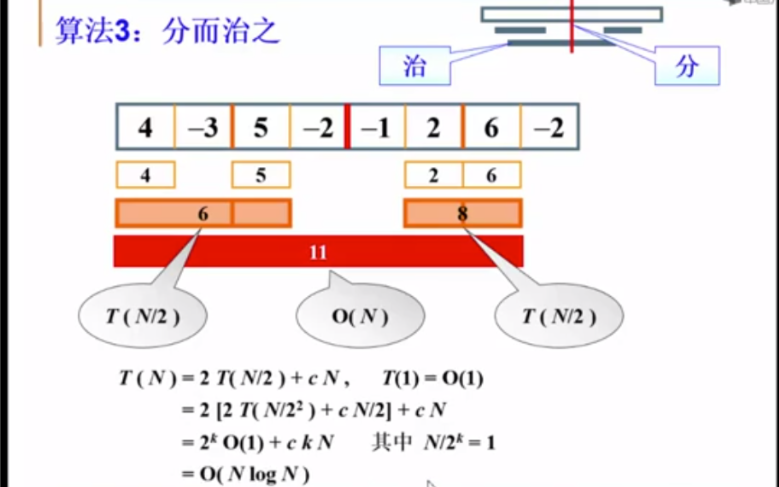
分治算法求解：

#include <stdio.h>
#define max(a,b) a>b?a:b

//---------------------------------
//
// 需求：
// 给定一个整数序列，求其中整数加起来最大子序列和（因为该数列中可能有负数）
// 
//--------------------------------


//---------------------
//法1:直接翻译的解法（穷举法）
// 时间复杂度：O(n^3)
//-----------------------
int MaxSubseqSum1(int A[], int N) {
	int ThisSum, MaxSum = 0;
	int i, j;
	for (i = 0; i < N; i++) {//i是子列的左端位置
		for (j = i; j < N; j++) {//j是子列的右端位置
			ThisSum = 0;
			for (int z = i; z <= j; z++) {
				ThisSum += A[z];
				if (ThisSum > MaxSum) {
					MaxSum = ThisSum;
				}
			}
			
		}

	}
	return MaxSum;
}

//---------------
//法1的优化版：（穷举法优化）
// 画一个图即可理解，当i为定值时，只要累加j下标所对应的值，就可以找到从i起所对应的最大序列和，如此循环则可以找到所有遍历的最大序列和
// 时间复杂度：O(n^2)
//---------------
int MaxSubseqSum2(int A[], int N) {
	int ThisSum, MaxSum = 0;
	int i, j;
	for (i = 0; i < N; i++) {//i是子列的左端位置
		ThisSum = 0;
		for (j = i; j < N; j++) {//j是子列的右端位置
			ThisSum += A[j];
			if (ThisSum > MaxSum) {
				MaxSum = ThisSum;
			}
		}

	}
	return MaxSum;
}

//-----------------
//法3：分治思想
// 4，-3，5，-2，-1，2，6，-2
// 
// 设计：不会（参考编程珠玑）
// 
//------------------

//用于比较3个数值大小
float max1(float a, float b, float c) {
	if (a > b && a > c) {
		return a;
	}
	else if (b > a && b > c) {
		return b;
	}
	else {
		return c;
	}
}

float arr[] = { 4,-3,5,-2,-1,2,6,-2 };
float maxsum3(int L, int R) {

	if (L > R) {//表示数组中没有元素
		return 0;
	}
	if (L == R) {//只有一个元素返回该元素相对于0的最大值
		return max(0, arr[L]);
	}
	int m = (L + R) / 2;//中位数的下标

	/*
	以下两个for循环的目的：找出跨越对应的最大子序列和
	*/
	float Lmax = 0, sum = 0;
	for (int i = m; i >= L; i--) {
		sum += arr[i];
		Lmax = max(Lmax, sum);
	}

	float Rmax = 0;
		sum = 0;
	for (int i = m+1; i <= R; i++) {
		sum += arr[i];
		Rmax = max(Rmax, sum);
	}
	return max1(Lmax + Rmax, maxsum3(L, m), maxsum3(m+1, R));

}


int main(void) {
	
	float sumMax = maxsum3(0, 7);
	printf("%f\n", sumMax);
}

运行结果：