Sparse Table
RMQ 问题
Sparse Table 可用于解决这样的问题:给出一个 \(n\) 个元素的数组 \(a_1, a_2, \cdots, a_n\),支持查询操作计算区间 \([l,r]\) 的最小值(或最大值)。这种问题被称为区间最值查询问题(Range Minimum/Maximum Query,简称 RMQ 问题)。预处理的时间复杂度为 \(O(n \log n)\),预处理后数组 \(a\) 的值不可以修改,一次查询操作的时间复杂度为 \(O(1)\)。
例题:P2880 [USACO07JAN] Balanced Lineup G
有一个包含 \(n\) 个数的序列 \(h_i\),有 \(q\) 次询问,每次询问 \(h_{a_i}, h_{a_i + 1}, \cdots, h_{b_i - 1}, h_{b_i}\) 中最大值与最小值的差。
数据范围:\(1 \le n \le 5 \times 10^4, \ 1 \le q \le 1.8 \times 10^5, \ 1 \le h_i \le 10^6, \ a_i \le b_i\)。
分析:题目要求最大值和最小值的差难以直接求出,通常需要分别求解最大值和最小值。最直接的做法是每次遍历区间中的每一个数,记录最大值和最小值。这样可以正确求出正确答案,但是效率低下,时间复杂度高达 \(O(nq)\),无法通过本题。
之所以这样做效率低下,是因为所有询问区间可能有着大量的重叠,这些重叠部分被多次遍历到,因此产生了大量的重复。如果可以通过预处理得到一些区间的最小值,再通过这些区间拼凑每一个询问区间,就可以提高效率。
预处理前缀和可以拼凑出任意区间的和,但是这个思路不能直接搬到最值查询问题中。原因在于区间和可以从一个大区间中减去一部分小区间得到,而区间最值不行,所以只能用小区间去拼出大区间。如何选择预处理的区间就成为关键,选择的区间既要能够拼出任意区间,数量少又不能太多,并且预处理和查询都要高效。
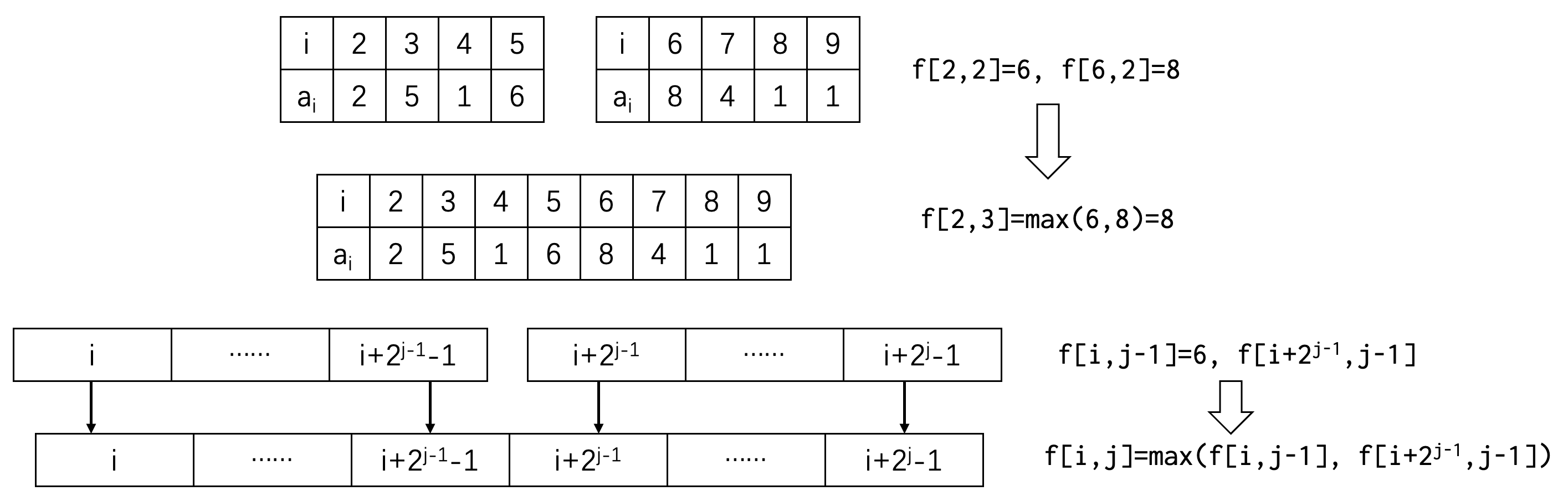
可以预处理以每一个位置为开头,长度为 \(2^0, 2^1, \cdots, 2^{\lfloor \log_2 n \rfloor}\) 的所有区间最值。下面以最大值为例,用 \(f_{i,j}\) 表示 \(h_i, h_{i+1}, \cdots, h_{i+2^j-2}, h_{i+2^j-1}\) 中的最大值,用递推的方式计算所有的 \(f\),转移为 \(f_{i,j} = \max (f_{i,j-1}, f_{i+2^{j-1}, j-1})\)。计算所有的 \(f\) 的过程为预处理,预处理的时间复杂度为 \(O(n \log n)\)。
void init() {
for (int i = 1; i <= n; i++) {
f[i][0] = h[i];
}
for (int j = 1; (1 << j) <= n; j++) {
for (int i = 1; i <= n - (1 << j) + 1; i++) {
f[i][j] = max(f[i][j - 1], f[i + (1 << (j - 1))][j - 1]);
}
}
}
接下来解决查询的问题,设需要查询最大值的区间是 \([l,r]\)。记区间长度为 \(L\),则该区间可以拆分为 \(O(\log L)\) 个小区间。对 \(L\) 做二进制拆分,从 \(l\) 开始向后跳,每次跳跃的量是一个 \(2\) 的幂,从而拼出整个区间。单词查询时间复杂度为 \(O(\log n)\)。
int query(int l, int r) {
int len = r - l + 1, ans = -INF, cur = l;
for (int i = 0; (1 << i) <= len; i++) {
if ((len >> i) & 1) {
ans = max(ans, f[cur][i]);
cur += (1 << i);
}
}
return ans;
}
更进一步,查询区间最值时,区间合并的过程允许重叠,因此只需要找到两个长度为 \(2^k\) 的区间合并得到 \([l,r]\)。令 \(k\) 为满足 \(2^k \le r-l+1\) 的最大整数,区间 \([l, l+2^k-1]\) 和区间 \([r-2^k+1,r]\) 合并起来覆盖了需要查询的区间 \([l,r]\)。

int query(int l, int r) {
int k = log_2[r - l + 1]; // 可以预处理log_2的表
return max(f[l][k], f[r - (1 << k) + 1][k]);
}
参考代码
#include <cstdio>
#include <algorithm>
using std::min;
using std::max;
const int N = 50005;
const int LOG = 16;
int h[N], f_min[N][LOG], f_max[N][LOG], log_2[N];
void init(int n) {
log_2[1] = 0;
for (int i = 2; i <= n; i++) log_2[i] = log_2[i >> 1] + 1; // 预处理对数表
for (int i = 1; i <= n; i++) {
f_min[i][0] = f_max[i][0] = h[i];
}
for (int j = 1; (1 << j) <= n; j++) {
for (int i = 1; i <= n - (1 << j) + 1; i++) {
f_min[i][j] = min(f_min[i][j - 1], f_min[i + (1 << (j - 1))][j - 1]);
f_max[i][j] = max(f_max[i][j - 1], f_max[i + (1 << (j - 1))][j - 1]);
}
}
}
int query(int l, int r, int flag) { // flag为1时查询最大值,为0时查询最小值
int k = log_2[r - l + 1];
if (flag) return max(f_max[l][k], f_max[r - (1 << k) + 1][k]);
else return min(f_min[l][k], f_min[r - (1 << k) + 1][k]);
}
int main()
{
int n, q; scanf("%d%d", &n, &q);
for (int i = 1; i <= n; i++) scanf("%d", &h[i]);
init(n);
for (int i = 1; i <= q; i++) {
int a, b; scanf("%d%d", &a, &b);
printf("%d\n", query(a, b, 1) - query(a, b, 0));
}
return 0;
}
Sparse Table 预处理部分的时间复杂度为 \(O(n \log n)\),查询一次的时间复杂度为 \(O(1)\),总的时间复杂度为 \(O(n \log n)\)。
实现细节:二维数组维度顺序分析
在实现稀疏表时,通常使用一个二维数组,例如 f[i][j]。这里的两个维度,一个代表区间的起始位置,另一个代表区间长度的对数。那么,f[position][log_length] 和 f[log_length][position] 这两种定义方式,哪一种更好呢?
在 C++ 等语言中,二维数组在内存中是按行主序存储的。这意味着 arr[i][j] 和 arr[i][j+1] 在内存中是相邻的,而 arr[i][j] 和 arr[i+1][j] 则可能相距很远。现代 CPU 依赖高速缓存(Cache)来提升性能,访问连续的内存区域(空间局部性)可以极大地提高缓存命中率,从而加速程序运行。
尽管两种写法在逻辑上都正确,但将长度维度放在第一维(f[LOG][N]),位置维度放在第二维,可以获得显著的性能提升,尤其是在 \(N\) 很大时。
习题:P3865 【模板】ST 表 & RMQ 问题
参考代码
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 100005;
const int LOG = 17;
int a[N]; // 原始数组
int st[LOG][N]; // 稀疏表
int Log2[N]; // 预计算 log2 值
inline int read() {
int x = 0, f = 1;
char ch = getchar();
while (ch < '0' || ch > '9') {
if (ch == '-') f = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = x * 10 + ch - 48;
ch = getchar();
}
return x * f;
}
// 预处理 Log2 数组
void precompute_log2(int n) {
Log2[1] = 0;
for (int i = 2; i <= n; ++i) {
Log2[i] = Log2[i / 2] + 1;
}
}
// 构建稀疏表
void build_sparse_table(int n) {
// 基础层:长度为 1 (2^0) 的区间,最大值就是元素本身
for (int j = 1; j <= n; ++j) {
st[0][j] = a[j];
}
// 逐层填充稀疏表
// i 从 1 开始,表示区间长度 2^1, 2^2, ...
for (int i = 1; i < LOG; ++i) {
// j 从 1 开始,表示区间的起始位置
// j + (1 << i) - 1 <= n 确保区间不越界
for (int j = 1; j + (1 << i) - 1 <= n; ++j) {
// st[i][j] = max(左半部分, 右半部分)
st[i][j] = max(st[i - 1][j], st[i - 1][j + (1 << (i - 1))]);
}
}
}
// 查询区间 [l, r] 的最大值
int query_rmq(int l, int r) {
// 计算 k,使得 2^k <= 区间长度 (r - l + 1)
int k = Log2[r - l + 1];
// 区间 [l, r] 可以被两个长度为 2^k 的区间覆盖:
// [l, l + 2^k - 1] 和 [r - 2^k + 1, r]
return max(st[k][l], st[k][r - (1 << k) + 1]);
}
int main() {
// 使用快速读入
int n = read();
int m = read();
for (int i = 1; i <= n; ++i) {
a[i] = read();
}
precompute_log2(n);
build_sparse_table(n);
for (int i = 0; i < m; ++i) {
int l = read();
int r = read();
printf("%d\n", query_rmq(l, r));
}
return 0;
}
习题:P1816 忠诚
参考代码
#include <cstdio>
#include <algorithm>
using namespace std;
const int M = 100005;
const int LOG = 17;
int a[M]; // 账目金额数组
int st[LOG][M]; // 稀疏表
int Log2[M]; // 预计算 log2 值
// 预处理 Log2 数组
void precompute_log2(int m) {
Log2[1] = 0;
for (int i = 2; i <= m; ++i) {
Log2[i] = Log2[i / 2] + 1;
}
}
// 构建稀疏表
void build_sparse_table(int m) {
// 基础层:长度为 1 (2^0) 的区间,最小值就是元素本身
for (int j = 1; j <= m; ++j) {
st[0][j] = a[j];
}
// 逐层填充稀疏表
// i 从 1 开始,表示区间长度 2^1, 2^2, ...
for (int i = 1; i < LOG; ++i) {
// j 从 1 开始,表示区间的起始位置
// j + (1 << i) - 1 <= m_val 确保区间不越界
for (int j = 1; j + (1 << i) - 1 <= m; ++j) {
// st[i][j] = min(左半部分, 右半部分)
st[i][j] = min(st[i - 1][j], st[i - 1][j + (1 << (i - 1))]);
}
}
}
// 查询区间 [a, b] 的最小值
int query_rmq(int a, int b) {
// 计算 k,使得 2^k <= 区间长度 (b - a + 1)
int k = Log2[b - a + 1];
// 区间 [a, b] 可以被两个长度为 2^k 的区间覆盖:
// [a, a + 2^k - 1] 和 [b - 2^k + 1, b]
return min(st[k][a], st[k][b - (1 << k) + 1]);
}
int main() {
int m, n;
scanf("%d%d", &m, &n);
for (int i = 1; i <= m; ++i) {
scanf("%d", &a[i]);
}
precompute_log2(m);
build_sparse_table(m);
for (int i = 0; i < n; ++i) {
int a_idx, b_idx;
scanf("%d%d", &a_idx, &b_idx);
if (i > 0) printf(" ");
printf("%d", query_rmq(a_idx, b_idx));
}
printf("\n");
return 0;
}
例题:P1198 [JSOI2008] 最大数
标准稀疏表不适用于元素会变化的动态数组,因为每次变动都可能需要重新预处理,成本过高。
本题的特殊之处在于序列只会在末尾添加元素,这样一来可以在每次添加新元素时,只更新稀疏表中与这个新元素相关的部分,而不是重建整个表。
为了方便在线更新,可以采用一种稍作修改的稀疏表定义:设 \(f_{i,j}\) 表示区间 \([j-2^i+1,j]\) 内的最大值,即以 \(j\) 为右端点、长度为 \(2^i\) 的区间的最大值。
参考代码
#include <iostream>
#include <algorithm>
using ll = long long;
using namespace std;
const int M = 200005;
const int LOG = 18; // ceil(log2(2e5)) = 18
ll a[M]; // 存储实际序列值, 1-indexed
// 稀疏表: st[i][j] 表示区间 [j - 2^i + 1, j] 的最大值
ll st[LOG][M];
int Log2[M]; // 预计算的 log2 值
ll D;
// 预处理 Log2 数组,用于 O(1) 计算 log
void init(int max_val) {
Log2[1] = 0;
for (int i = 2; i <= max_val; ++i) {
Log2[i] = Log2[i / 2] + 1;
}
}
// 在位置 p 插入新值 val,并在线更新稀疏表
void update(int p, ll val) {
a[p] = val;
// 更新 ST 表的第 0 层
st[0][p] = a[p];
// 逐层向上更新所有以 p 为右端点的 ST 表项
for (int i = 1; (1 << i) <= p; ++i) {
// st[i][p] 覆盖区间 [p - 2^i + 1, p]
// 它的值是两个长度为 2^(i-1) 的子区间的最大值:
// 1. [p - 2^i + 1, p - 2^(i-1)],其最大值为 st[i-1][p - (1 << (i-1))]
// 2. [p - 2^(i-1) + 1, p],其最大值为 st[i-1][p]
st[i][p] = max(st[i-1][p], st[i-1][p - (1 << (i-1))]);
}
}
// 查询区间 [l, r] 的最大值
ll query(int l, int r) {
if (l > r) return 0;
// 计算 k,使得 2^k <= 区间长度
int k = Log2[r - l + 1];
// 区间 [l, r] 可以被两个长度为 2^k 的区间覆盖:
// 1. [l, l + 2^k - 1]
// 2. [r - 2^k + 1, r]
// 第一个区间的最大值是 st[k][l + (1 << k) - 1]
// 第二个区间的最大值是 st[k][r]
return max(st[k][l + (1 << k) - 1], st[k][r]);
}
int main() {
int m;
cin >> m >> D;
init(m);
ll t = 0; // 最近一次查询操作的答案
int len = 0; // 当前数列的长度
for (int i = 0; i < m; ++i) {
char op;
ll val;
cin >> op >> val;
if (op == 'A') {
len++;
ll new_val = (val + t) % D;
update(len, new_val);
} else { // op == 'Q'
int l = val;
// 查询末尾 l 个数,即区间 [len - l + 1, len]
t = query(len - l + 1, len);
cout << t << "\n";
}
}
return 0;
}
例题:P7333 [JRKSJ R1] JFCA
分析:看到环形,先破环成链。
看起来每个点的答案 \(O(1)\) 求得不太容易,但每个点的答案具有二分性。
对于每个点,二分答案,查询左右两段区间的最大值看是否大于等于 \(b_i\)。
因为没有修改,所以区间最值可以用 Sparse Table 维护,总体时间复杂度为 \(O(n \log n)\)。
参考代码
#include <cstdio>
#include <algorithm>
using std::max;
using std::min;
const int N = 300005;
const int LOG = 17;
int a[N], b[N], log_2[N], st[N][LOG], ans[N];
int query(int l, int r) {
int len = log_2[r - l + 1];
return max(st[l][len], st[r - (1 << len) + 1][len]);
}
int main()
{
int n; scanf("%d", &n);
for (int i = 2; i <= n; i++) log_2[i] = log_2[i / 2] + 1;
for (int i = 1; i <= n; i++) {
// 破环成链
scanf("%d", &a[i]); a[i + n * 2] = a[i + n] = a[i];
st[i][0] = st[i + n][0] = st[i + n * 2][0] = a[i];
ans[i] = n;
}
// Sparse Table 维护区间最大值
for (int j = 1; (1 << j) <= n; j++) {
for (int i = 1; i <= 3 * n - (1 << j) + 1; i++) {
st[i][j] = max(st[i][j - 1], st[i + (1 << (j - 1))][j - 1]);
}
}
for (int i = 1; i <= n; i++) scanf("%d", &b[i]);
for (int i = n + 1; i <= n * 2; i++) {
// left 二分左边第一个位置
int l = i - n + 1, r = i - 1, res = -1;
while (l <= r) {
int mid = (l + r) / 2;
if (query(mid, i - 1) >= b[i - n]) {
l = mid + 1; res = mid;
} else {
r = mid - 1;
}
}
if (res != -1) ans[i - n] = min(ans[i - n], i - res);
// right 二分右边第一个位置
l = i + 1; r = i + n - 1; res = -1;
while (l <= r) {
int mid = (l + r) / 2;
if (query(i + 1, mid) >= b[i - n]) {
r = mid - 1; res = mid;
} else {
l = mid + 1;
}
}
if (res != -1) ans[i - n] = min(ans[i - n], res - i);
}
for (int i = 1; i <= n; i++) printf("%d ", ans[i] == n ? -1 : ans[i]);
return 0;
}
习题:P8818 [CSP-S 2022] 策略游戏
解题思路
这是一个典型的二人零和博弈,可以通过最大最小化模型来分析双方的最优策略。
- 小 L 的视角:小 L 先手选择 \(x\),他知道在他做出选择后,小 Q 会采取最优策略来让分数变得尽可能小。因此,小 L 必须选择一个 \(x\),使得“小 Q 能造成的最小分数”这个值最大。
- 小 Q 的视角:当小 L 选定一个 \(x\) 后,小 Q 的任务就变成了在 \(B_{l_2 \dots r_2}\) 中选择一个 \(y\),使得 \(A_x \cdot B_y\) 最小。
- 设 \(\min_B\) 和 \(\max_B\) 分别是 B 在区间 \([l_2,r_2]\) 的最小值和最大值。
- 如果 \(A_x \gt 0\),为了使乘积最小,小 Q 显然会选择 \(\min_B\)。
- 如果 \(A_x \lt 0\),为了使乘积最小,小 Q 会选择 \(\max_B\)。
- 如果 \(A_x = 0\),乘积恒为 0。
所以,对于小 L 选定的 \(x\),他能确保的得分是:
小 L 会遍历所有可选的 \(x\)(在 \([l_1,r_1]\) 中),计算出每个 \(x\) 对应的 \(\text{score}(x)\),并选择那个能使 \(\text{score}(x)\) 最大的 \(x\)。
最终的游戏得分就是:
直接遍历所有 \(x\) 会导致 \(O(N)\) 的查询复杂度,总复杂度为 \(O(NQ)\),会超时,需要优化求 \(\max\{\text{score}(x)\}\) 的过程。
把小 L 的选择按 \(A_x\) 的正负性分开讨论:
- 如果小 L 选择一个正数 \(A_x\)
- 他期望的得分为 \(A_x \cdot \min_B\),为了最大化这个值
- 若 \(\min_B \ge 0\),\(A_x\) 越大越好,小 L 会选择 A 区间中最大的正数。
- 若 \(\min_B \lt 0\),\(A_x\) 越小越好,小 L 会选择 A 区间中最小的正数。
- 他期望的得分为 \(A_x \cdot \min_B\),为了最大化这个值
- 如果小 L 选择一个负数 \(A_x\)
- 他期望的得分为 \(A_x \cdot \max_B\),为了最大化这个值(使其尽可能接近 0 或变为正数)
- 若 \(\max_B \ge 0\),\(A_x\) 越接近 0 越好,小 L 会选择 A 区间中最大的负数。
- 若 \(\max_B \lt 0\),\(A_x\) 越小越好,小 L 会选择 A 区间中最小的负数。
- 他期望的得分为 \(A_x \cdot \max_B\),为了最大化这个值(使其尽可能接近 0 或变为正数)
- 如果小 L 选择一个 \(A_x = 0\),他能确保得分为 0
综上,小 L 的最优决策只依赖于 \(A_{l_1 \dots r_1}\) 区间内的几个关键值:最大的正数、最小的正数、最大的负数、最小的负数,以及是否存在 0。同时,他也需要知道 \(B_{l_2 \dots r_2}\) 区间的最大值和最小值。
这些“区间关键值”的查询都属于静态区间最值查询问题,由于数组 A 和 B 是不变的,可以使用稀疏表来进行预处理,以达到查询时 \(O(1)\) 的效率。
参考代码
#include <cstdio>
#include <algorithm>
using ll = long long;
using namespace std;
const int N = 100005;
const int LOG = 17;
const ll INF = 4e18;
// A 数组的稀疏表节点结构
struct NodeA {
ll max_pos; // 区间内最大的正数
ll min_pos; // 区间内最小的正数
ll max_neg; // 区间内最大的负数 (最接近0)
ll min_neg; // 区间内最小的负数 (绝对值最大)
bool has_zero;
};
// B 数组的稀疏表节点结构
struct NodeB {
ll min_val;
ll max_val;
};
// 全局变量
int n, m, q;
ll a[N], b[N];
NodeA st_a[LOG][N];
NodeB st_b[LOG][N];
int Log2[N];
// 合并两个 NodeA 节点
NodeA mergeA(const NodeA& left, const NodeA& right) {
return {
max(left.max_pos, right.max_pos),
min(left.min_pos, right.min_pos),
max(left.max_neg, right.max_neg),
min(left.min_neg, right.min_neg),
left.has_zero || right.has_zero
};
}
// 合并两个 NodeB 节点
NodeB mergeB(const NodeB& left, const NodeB& right) {
return {
min(left.min_val, right.min_val),
max(left.max_val, right.max_val)
};
}
// 预处理 Log2 数组
void init(int n) {
Log2[1] = 0;
for (int i = 2; i <= n; ++i) {
Log2[i] = Log2[i / 2] + 1;
}
}
// 构建 A 数组的稀疏表
void build_A() {
for (int j = 1; j <= n; ++j) {
if (a[j] > 0) {
st_a[0][j] = {a[j], a[j], -INF, INF, false};
} else if (a[j] < 0) {
st_a[0][j] = {-INF, INF, a[j], a[j], false};
} else {
st_a[0][j] = {-INF, INF, -INF, INF, true};
}
}
for (int i = 1; i < LOG; ++i) {
for (int j = 1; j + (1 << i) - 1 <= n; ++j) {
st_a[i][j] = mergeA(st_a[i - 1][j], st_a[i - 1][j + (1 << (i - 1))]);
}
}
}
// 构建 B 数组的稀疏表
void build_B() {
for (int j = 1; j <= m; ++j) {
st_b[0][j] = {b[j], b[j]};
}
for (int i = 1; i < LOG; ++i) {
for (int j = 1; j + (1 << i) - 1 <= m; ++j) {
st_b[i][j] = mergeB(st_b[i - 1][j], st_b[i - 1][j + (1 << (i - 1))]);
}
}
}
// 查询 A 数组的区间信息
NodeA query_A(int l, int r) {
int k = Log2[r - l + 1];
return mergeA(st_a[k][l], st_a[k][r - (1 << k) + 1]);
}
// 查询 B 数组的区间信息
NodeB query_B(int l, int r) {
int k = Log2[r - l + 1];
return mergeB(st_b[k][l], st_b[k][r - (1 << k) + 1]);
}
int main() {
scanf("%d%d%d", &n, &m, &q);
for (int i = 1; i <= n; ++i) scanf("%lld", &a[i]);
for (int i = 1; i <= m; ++i) scanf("%lld", &b[i]);
init(max(n, m));
build_A();
build_B();
while (q--) {
int l1, r1, l2, r2;
scanf("%d%d%d%d", &l1, &r1, &l2, &r2);
NodeA resA = query_A(l1, r1);
NodeB resB = query_B(l2, r2);
ll min_b = resB.min_val;
ll max_b = resB.max_val;
ll ans = -INF;
// Case 1: 小 L 选择正数 A[x]
if (resA.max_pos != -INF) { // 检查是否存在正数
if (min_b >= 0) {
ans = max(ans, resA.max_pos * min_b);
} else {
ans = max(ans, resA.min_pos * min_b);
}
}
// Case 2: 小 L 选择负数 A[x]
if (resA.min_neg != INF) { // 检查是否存在负数
if (max_b >= 0) {
ans = max(ans, resA.max_neg * max_b);
} else {
ans = max(ans, resA.min_neg * max_b);
}
}
// Case 3: 小 L 选择 0
if (resA.has_zero) {
ans = max(ans, 0ll);
}
printf("%lld\n", ans);
}
return 0;
}
习题:P7809 [JRKSJ R2] 01 序列
解题思路
由于序列只包含 0 和 1,这两种子序列的结构非常特殊,可以利用这一性质来高效地回答查询。
对于一个 01 序列,严格上升的子序列只能是 0、1 或 0, 1。因此,LIS 的长度只可能是 1 或 2。
- 长度为 1:如果区间 \([l,r]\) 内只包含一种数字(全是 0 或全是 1),或者虽然两种数字都存在,但所有的 1 都出现在所有的 0 之前(例如 1, 1, 0, 0),那么就无法构成 0, 1 的子序列,此时 LIS 长度为 1。
- 长度为 2:如果区间内至少存在一个 0 出现在了某个 1 的前面,那么总能从中挑选出一个 0 和一个 1 构成长度为 2 的 LIS。
因此,问题转化为如何快速判断“区间内是否存在一个 0 在某个 1 之前”,一个高效的判断方法是检查区间内第一个 0 的位置是否小于区间内最后一个 1 的位置。
可以进行 \(O(N)\) 的预处理:
- \(\text{f0}_i\):从位置 \(i\) 开始向后(包括 \(i\))遇到的第一个 0 的索引。
- \(\text{l1}_i\):从位置 \(i\) 开始向前(包括 \(i\))遇到的最后一个 1 的索引。
对于查询 \((l,r)\),区间内第一个 0 的位置就是 \(\text{f0}_l\),最后一个 1 的位置就是 \(\text{l1}_r\),只需比较 \(\text{f0}_l\) 和 \(\text{l1}_r\) 即可。如果 \(\text{f0}_l \lt \text{l1}_r\),说明存在一个 0 在 1 前面,LIS 长度为 2,否则为 1,此方法也自然地处理了区间内只有一种数字的情况。
对于 01 序列,不下降子序列的形式必然是 \(0, 0, \dots, 0, 1, 1, \dots, 1\),可以分三种情况讨论其最大长度:
- 只由 0 构成:长度为区间 \([l,r]\) 中 0 的个数。
- 只由 1 构成:长度为区间 \([l,r]\) 中 1 的个数。
- 由 0 和 1 共同构成:可以选择一个分割点 \(k\)(\(l \le k \lt r\)),取 \([l,k]\) 中所有的 0,以及 \([k+1,r]\) 中所有的 1,来构成一个不下降子序列,其长度为 \(\text{count}_0(l,k) + \text{count}_1(k+1,r)\),需要找到最优的 \(k\) 使得这个和最大。
为了高效计算,预处理前缀和与后缀和:
- \(\text{pre}_i\):序列前 \(i\) 个数中 0 的个数。
- \(\text{suf}_i\):序列从第 \(i\) 个数到末尾中 1 的个数。
那么,\(\text{count}_0(l,k) = \text{pre}_k - \text{pre}_{l-1}\),\(\text{count}_1(k+1,r) = \text{suf}_{k+1} - \text{suf}_{r+1}\),第 3 种情况的长度为 \((\text{pre}_k - \text{pre}_{l-1}) + (\text{suf}_{k+1} - \text{suf}_{r+1})\),整理得到 \((\text{pre}_k + \text{suf}_{k+1}) - (\text{pre}_{l-1} + \text{suf}_{r+1})\)。
对于一个固定的查询 \((l,r)\),\(\text{pre}_{l-1} + \text{suf}_{r+1}\) 是一个常数。因此,为了使总长度最长,只需要找到 \(\max \limits_{k=l}^{r-1} \{ \text{pre}_k + \text{suf}_{k+1} \}\)。
这是一个经典的区间最值查询问题,可以预处理一个新数组 \(v_i = \text{pre}_i + \text{suf}_{i+1}\),然后对其构建一个稀疏表。这样,就能在 \(O(1)\) 的时间内查询任意区间的最大值。
最终,类型 1 查询的答案就是上述三种情况中的最大值。
参考代码
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 1000005;
const int LOG = 20;
int a[N];
int pre[N], suf[N];
int st[LOG][N];
int log_2[N];
int f0[N], l1[N]; // f0[i]:i及之后第一个0的位置; l1[i]:i及之前最后一个1的位置
int query(int l, int r) {
int k = log_2[r - l + 1];
return max(st[k][l], st[k][r - (1 << k) + 1]);
}
int main()
{
int n, m;
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]);
if (i > 1) log_2[i] = log_2[i / 2] + 1; // 预处理log2
}
l1[0] = 0;
for (int i = 1; i <= n; i++) {
pre[i] = pre[i - 1] + (a[i] == 0);
l1[i] = a[i] == 1 ? i : l1[i - 1];
}
f0[n + 1] = n + 1;
suf[n + 1] = 0;
for (int i = n; i >= 1; i--) {
suf[i] = suf[i + 1] + (a[i] == 1);
// st[0][i] 存储 LNDS 类型1中需要RMQ的数组 V[i] = pre[i] + suf[i+1]
st[0][i] = pre[i] + suf[i + 1];
f0[i] = a[i] == 0 ? i : f0[i + 1];
}
for (int i = 1; i < LOG; i++) {
int len = 1 << i;
for (int j = 1; j <= n - len + 1; j++) {
st[i][j] = max(st[i - 1][j], st[i - 1][j + len / 2]);
}
}
for (int i = 1; i <= m; i++) {
int op, l, r; scanf("%d%d%d", &op, &l, &r);
if (l == r) { // 区间长度为1,答案必为1
printf("1\n");
continue;
}
if (op == 1) { // 查询LNDS
// Case 1 & 2: 全0子序列 或 全1子序列
int tmp = max(pre[r] - pre[l - 1], suf[l] - suf[r + 1]);
// Case 3: 0...1...子序列,通过RMQ找到最优分割点
// max(pre[k]+suf[k+1]) for k in [l,r-1] - (pre[l-1]+suf[r+1])
tmp = max(query(l, r - 1) - pre[l - 1] - suf[r + 1], tmp);
printf("%d\n", tmp);
} else { // 查询LIS
// LIS长度为2 <=> 区间内第一个0的位置 < 区间内最后一个1的位置
// f0[l]是[l,n]中第一个0的位置, l1[r]是[1,r]中最后一个1的位置
// 如果 f0[l] < l1[r],则这两个0和1都在[l,r]内且顺序正确
printf("%d\n", f0[l] < l1[r] ? 2 : 1);
}
}
return 0;
}
习题:P6648 [CCC 2019] Triangle: The Data Structure
给定一个大小为 \(n\) 的数字三角形和一个整数 \(k\),需要找出其中所有大小为 \(k\) 的子三角形,计算每个子三角形中所有元素的最大值,并求出这些最大值的总和。
解题思路
一个直接的想法是遍历所有可能的子三角形,时间复杂度为 \(O(n^2 k^2)\),显然超时。
为了优化寻找最大值的过程,可以使用动态规划的思想。这个问题的结构类似于二维稀疏表的思想,利用预计算好的小区域信息来快速查询大区域的信息。
定义 \(f_{s,i,j}\) 为以 \((i,j)\) 为最上方顶点的、大小为 \(s\) 的子三角形内的最大值,目标是求出所有 \(f_{k,i,j}\) 的和。
如果从 \(s-1\) 推导 \(s\) 是可行的,但是时间复杂度为 \(O(n^2 k)\),依然超时。
一种更高效的拆分方式是:
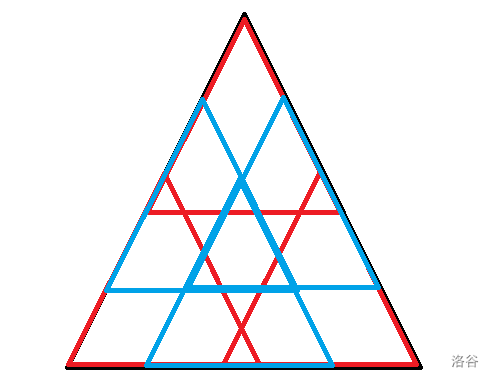
参考代码
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
using ll = long long;
const int N = 3005;
// a[i][j]: 存储输入的三角形,(i, j) 表示第 i 行第 j 个元素
int a[N][N];
// dp[u][i][j]: DP 状态数组。u 是滚动数组索引 (0或1)。
// dp[u][i][j] 存储了以 (i, j) 为顶点的、特定大小的子三角形内的最大值。
// DP过程会从小尺寸的三角形开始计算,逐步推导到目标尺寸k。
int dp[2][N][N];
int main()
{
int n, k;
scanf("%d%d", &n, &k);
ll sum = 0;
// 读入三角形数据
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= i; j++) {
scanf("%d", &a[i][j]);
sum += a[i][j]; // 同时计算所有元素的总和
}
}
// 特殊情况:如果子三角形大小为1,那么每个元素本身就是一个子三角形。
// 最大值的和就是所有元素的总和。
if (k == 1) {
printf("%lld\n", sum);
} else {
// DP 优化思路:
// 任何大小为 k 的三角形都可以由若干个更小的三角形覆盖。
// 本算法采用 (k+1)/2 的方式递归地将问题分解。
// 从大小为 2 的三角形开始,逐步计算更大尺寸三角形内的最大值,直到尺寸为 k。
vector<int> step; // 存储DP要计算的三角形尺寸序列
int tmp = k;
// 生成尺寸序列,例如 k=7 -> steps: 7, 4。最终会反转为 4, 7。
while (tmp != 2) {
step.push_back(tmp);
tmp = (tmp + 1) / 2;
}
reverse(step.begin(), step.end()); // 反转序列,从小尺寸开始DP
// DP 的基础情况:计算所有尺寸为 2 的子三角形的最大值。
// 一个以 (i, j) 为顶点的尺寸为 2 的三角形包含 a[i][j], a[i+1][j], a[i+1][j+1]。
for (int i = 1; i < n; i++) {
for (int j = 1; j <= i; j++) {
dp[0][i][j] = max(a[i][j], max(a[i + 1][j], a[i + 1][j + 1]));
}
}
int u = 0; // 滚动数组的当前索引
int pre = 2; // 上一个计算的三角形尺寸,初始为2
// 动态规划主循环,u^1 是上一个状态,u 是当前状态
for (int x : step) { // x 是当前要计算的三角形尺寸
u ^= 1; // 切换滚动数组
// 遍历所有以 (i, j) 为顶点的、尺寸为 x 的子三角形
for (int i = 1; i <= n - x + 1; i++) {
for (int j = 1; j <= i; j++) {
// 核心递推关系:
// 一个尺寸为 x 的大三角形,可以被6个尺寸为 pre 的小三角形完全覆盖。
// 通过取这6个预先计算好的小三角形最大值的最大值,得到大三角形的最大值。
// 这是一种空间换时间的优化,避免了对大三角形内部所有元素的遍历。
int res = dp[u^1][i][j]; // 1. 左上角
res = max(res, dp[u^1][i + x - pre][j]); // 2. 左下角
res = max(res, dp[u^1][i + x - pre][j + x - pre]); // 3. 右下角
int midi = i + (x - 1) / 2;
int midj = j + (x - 1) / 2;
int half = (pre + 1) / 2;
// 另外三个位于中间部分的子三角形
res = max(res, dp[u^1][midi - half + 1][j]); // 4.
res = max(res, dp[u^1][midi - half + 1][midj - half + 1]); // 5.
res = max(res, dp[u^1][i + x - pre][midj - half + 1]); // 6.
dp[u][i][j] = res;
}
}
pre = x; // 更新上一个尺寸
}
ll ans = 0;
// DP完成后,dp[u] 中存储了所有尺寸为 k 的子三角形的最大值。
// 遍历所有尺寸为 k 的子三角形的顶点,累加它们的最大值。
for (int i = 1; i <= n - k + 1; i++) {
for (int j = 1; j <= i; j++) {
ans += dp[u][i][j];
}
}
printf("%lld\n", ans);
}
return 0;
}
习题:P2048 [NOI2010] 超级钢琴
解题思路
利用前缀和数组 \(S\),任意区间 \([i,j]\) 可以表示为 \(S_j - S_{i-1}\)。对于一个固定的右端点 \(j\),要使区间和最大,必须在所有合法的左端点 \(i\) 中,找到一个使 \(S_{i-1}\) 最小的。
根据长度限制 \(L \le j-i+1 \le R\),对于 \(S_{i-1}\) 的索引 \(p=i-1\),其取值范围是 \([\max(0,j-R),j-L]\)。因此,对每个右端点 \(j\),都存在一个“最优”的左端点,使得区间和最大。
全局第 1 大的和弦,一定是某个右端点 \(j\) 对应的最优和弦。但全局第 2 大的和弦,可能是另一个右端点 \(j'\) 对应的最优和弦,也可能是 \(j\) 对应的次优和弦,无法预知,因此需要一个能动态比较所有这些可能性的方法。
可以用一个大顶堆来解决这个问题,堆中存放代表“候选和弦”的对象,每个对象记录了其和、右端点、以及它可选的左端点范围。
对于每个可能的右端点 \(j \in [L, n]\),先找出它对应的最优和弦。这可以通过在范围 \([\max(0,j-R), j-L]\) 内查询前缀和数组 \(S\) 的最小值来完成。这个查询是一个 RMQ 问题,可以用稀疏表在 \(O(1)\) 时间内解决(预处理需要 \(O(n \log n)\)),将这 \(n-L+1\) 个“各自最优”的和弦放入堆中。
重复 \(k\) 次以下操作:
- 从堆中取出堆顶元素,这是当前所有候选中的最优解,计入总答案。
- 假设这个最优解的右端点是 \(j\),它使用了左端点(对应的前缀和索引)\(p\),现在已经用掉了这个组合。
- 为了“生成”右端点 \(j\) 的次优解,将 \(p\) 从可选范围中排除,这相当于将原范围以 \(p\) 为界分裂成两个子范围。在这两个子范围中再次使用 RMQ 寻找新的最优左端点,从而生成两个新的“候选和弦”,并将它们放入堆中。
这个过程保证了每次取出的都是全局的下一个最大值,\(k\) 次迭代后,就得到了前 \(k\) 大和弦的和。
时间复杂度为 \(O((n+k)\log n)\),其中 \(O(n \log n)\) 用于构建稀疏表和初始化堆,\(O(k \log n)\) 用于 \(k\) 次的堆操作。
参考代码
#include <cstdio>
#include <queue>
using namespace std;
using ll = long long;
const int N = 5e5 + 5;
const int LOG = 19;
int n, k, l, r;
ll s[N]; // 前缀和数组,s[i] = a[1] + ... + a[i]
// 稀疏表用于 RMQ
// st_val 存区间最小值,st_idx 存最小值对应的索引
ll st_val[LOG][N];
int st_idx[LOG][N];
int Log2[N];
// 优先队列中存储的节点
struct Node {
ll sum; // 当前区间的和
int end; // 区间的右端点
int pl, pr; // 可选的左端点前缀和索引范围 [pl, pr]
// 重载小于号,用于大顶堆
bool operator<(const Node& other) const {
return sum < other.sum;
}
};
// 构建稀疏表
void build() {
Log2[1] = 0;
for (int i = 2; i <= n; i++) Log2[i] = Log2[i / 2] + 1;
for (int i = 0; i <= n; i++) {
st_val[0][i] = s[i];
st_idx[0][i] = i;
}
for (int i = 1; i < LOG; i++) {
for (int j = 0; j + (1 << i) - 1 <= n; j++) {
ll val1 = st_val[i - 1][j];
ll val2 = st_val[i - 1][j + (1 << (i - 1))];
if (val1 <= val2) {
st_val[i][j] = val1;
st_idx[i][j] = st_idx[i - 1][j];
} else {
st_val[i][j] = val2;
st_idx[i][j] = st_idx[i - 1][j + (1 << (i - 1))];
}
}
}
}
// 查询 [l, r] 范围内的最小值索引
int query(int l, int r) {
int k = Log2[r - l + 1];
ll val1 = st_val[k][l];
ll val2 = st_val[k][r - (1 << k) + 1];
if (val1 <= val2) return st_idx[k][l];
else return st_idx[k][r - (1 << k) + 1];
}
int main()
{
scanf("%d%d%d%d", &n, &k, &l, &r);
s[0] = 0;
for (int i = 1; i <= n; i++) {
ll a; scanf("%lld", &a);
s[i] = s[i - 1] + a;
}
build();
priority_queue<Node> pq;
// 初始化优先队列
for (int i = l; i <= n; i++) {
int pl = i - r;
int pr = i - l;
if (pl < 0) pl = 0;
int p = query(pl, pr);
ll sum = s[i] - s[p];
pq.push({sum, i, pl, pr});
}
ll ans = 0;
while (k--) {
Node t = pq.top(); pq.pop();
ans += t.sum;
int i = t.end;
int pl = t.pl;
int pr = t.pr;
// 找到刚刚使用的最优左端点前缀和的索引 p
int p = query(pl, pr);
// 将原区间分裂,寻找次优解并加入队列
// 1. 在 [pl, p - 1] 中寻找新的最优解
if (pl < p) {
int pbl = query(pl, p - 1);
pq.push({s[i] - s[pbl], i, pl, p - 1});
}
// 2. 在 [p + 1, pr] 中寻找新的最优解
if (p < pr) {
int pbr = query(p + 1, pr);
pq.push({s[i] - s[pbr], i, p + 1, pr});
}
}
printf("%lld\n", ans);
return 0;
}
稀疏表优化动态规划
动态规划是解决最优化问题的强大工具,一种典型的 DP 状态转移方程是:\(f_i = \min \limits_{j=0}^{i-1} \{ f_j + \text{cost}(j,i) \}\)。
如果对于每个 \(i\),都需要遍历所有可能的 \(j\) 来寻找最优决策,那么 DP 的总时间复杂度通常会是 \(O(N^2)\)。当数据规模达到 \(10^5\) 级别时,\(O(N^2)\) 的算法将无法在规定时间内完成。
此时,需要对决策过程进行优化。如果转移方程中的 \(\min\) 或 \(\max\) 操作是在一个连续的区间上进行的,即 \(f_i = \min \limits_{j=l_i}^{r_i} \{ f_j \} + \text{cost}(i)\),那么这个问题就转化为了一个经典的区间最值查询问题,可以使用稀疏表来优化整个 DP 的复杂度。
标准稀疏表用于静态数组,但在 DP 问题中,\(f\) 数组是逐个计算的,无法一开始就对整个 \(f\) 数组进行预处理,因此需要“动态地”构建稀疏表。
假设 \(f_p\) 的值被计算出来,用它来更新稀疏表:
void update(int p, int val) {
// 首先设置 ST 表的第 0 层,即长度为 2^0=1 的区间
st[0][p] = val;
// 逐层向上更新
// st[i][p] 在此代码中覆盖区间 [p - (1<<i) + 1, p]
for (int i = 1; (1 << i) <= p + 1; i++) {
int mid = p - (1 << (i - 1));
// st[i][p] 由两个长度为 2^(i-1) 的子区间合并而来
st[i][p] = min(st[i - 1][p], st[i - 1][mid]);
}
}
这个
update操作只更新与新计算出的 \(f_p\) 相关的信息,因此时间复杂度为 \(O(\log n)\)。
例题:P8592 『JROI-8』颅脑损伤 2.0(加强版)
首先分析染色条件,条件 1 和 2 合在一起,等价于必须选择一个由若干条互不相交的线段组成的子集(红色线段集合 \(R\)),这个子集需要“覆盖”所有的输入线段。
这里的“覆盖”指的是对于原集合中的任意一条线段 \(s\),要么 \(s\) 本身就是一条红色线段(\(s\) 属于 \(R\)),要么 \(s\) 与 \(R\) 中的某条红色线段相交。
目标就是找到满足这个条件的、总长度最小的红色线段集合 \(R\)。
这是一个在区间上进行决策的优化问题,很自然地可以想到使用动态规划。为了让问题具有清晰的阶段性,首先需要对所有线段进行排序,按右端点 \(r\) 从小到大排序是处理此类问题的经典策略。如果右端点相同,则按左端点 \(l\) 排序。
设 \(f_i\) 表示为了覆盖排序后的前 \(i\) 条线段,并且强制要求第 \(i\) 条线段被染成红色时,所需要的最小红色线段长度和。
如果 \(i\) 是红色的,它会覆盖所有与它相交的线段。那么,那些没有被 \(i\) 覆盖的、并且在线段 \(i\) 之前的线段,就必须由 \(i\) 左侧的其他红色线段来覆盖。
哪些线段 \(k\)(\(k \lt i\))没有被 \(i\) 覆盖呢?因为是按 \(r\) 排序的,所以 \(r_k \le r_i\),\(k\) 不与 \(i\) 相交的唯一可能是 \(r_k \lt l_i\)。
设 \(p\) 是满足 \(r_p \lt l_i\) 的最大索引,这意味着线段 \(1 \sim p\) 都不能被 \(i\) 覆盖,它们必须由 \(i\) 左侧的红色线段集合来解决,而线段 \(p+1 \sim i-1\) 都被 \(i\) 覆盖。
因此,计算 \(f_i\) 的问题分解为两部分:
- \(i\) 自身的长度 \(r_i - l_i\)
- 覆盖 \(1 \sim p\) 的最小代价,这个代价可以通过选择 \(1 \sim p\) 中的某条线段 \(k\) 作为这个前缀部分的“最后一条”红色线段来完成,其成本就是 \(f_k\)。需要在所有合法的 \(k\) 中取一个最优的,即 \(\min \{ f_k \}\)。
\(\min \{ f_k \}\) 就是 \(\min \limits_{k=1 \dots p} f_{k}\) 吗?不是的,需要满足 \(r_k \ge \max (l_1, \dots, l_p)\),因为这样才能确保所有 \(1 \sim p\) 之间的黑色线段都被红色线段覆盖。
由于 \(r\) 在排序后是有序的,\(p\) 可以通过二分查找在 \(O(\log N)\) 时间内找到,这就是转移方程中 \(k\) 的上界。\(\max (l_1, \dots, l_p)\) 是一个前缀最大值,可以预处理,这样一来 \(k\) 的下界也可以通过二分查找找到。于是 \(k\) 的可选范围是一个区间,DP 的计算变成了经典的区间最小值查询问题。
\(f_i\) 代表的是以 \(i\) 为红色结尾的方案代价,最终的染色方案其最右的红色线段可能是任何一个,因此需要在所有可能的 \(f_i\) 中找到一个全局最优解。
一个合法的染色方案必须覆盖所有 \(n\) 条线段,如果 \(i\) 是方案中最右的红色线段,它必须有能力覆盖 \(i+1 \sim n\) 的线段。一个简单的判定条件是 \(r_i\) 必须大于等于所有线段的左端点的最大值,即 \(r_i \ge \max \{l\}\)。所以,最终答案是所有满足 \(r_i \ge \max\{l\}\) 的 \(f_i\) 中的最小值。
参考代码
#include <cstdio>
#include <algorithm>
using namespace std;
// 定义常量
const int N = 500005;
const int LOG = 19; // log2(500005) 约等于 18.9
const int INF = 1e9 + 5;
// 线段结构体
struct Segment {
int l, r;
// 重载小于号,用于排序:优先按右端点 r 升序,r 相同则按 l 升序
bool operator<(const Segment& other) const {
return r != other.r ? r < other.r : l < other.l;
}
};
Segment a[N];
int dp[N]; // dp[i]: 表示覆盖前 i 个线段且 a[i] 为红色的最小代价
int maxl[N]; // maxl[i]: 前 i 个线段中左端点的最大值 (max(a[1].l, ..., a[i].l))
int st[LOG][N]; // 稀疏表,用于 RMQ (区间最小值查询)
int Log2[N]; // 预处理 log2 的值
// 预处理 Log2 数组,用于稀疏表
void init(int n) {
Log2[1] = 0;
for (int i = 2; i <= n; i++) Log2[i] = Log2[i / 2] + 1;
}
// 更新稀疏表。这是一个动态更新,在计算 dp[p] 后调用
void update(int p, int val) {
st[0][p] = val; // ST 表的底层是 dp 值
// 逐层向上更新,st[i][p] 覆盖区间 [p - (1<<i) + 1, p]
for (int i = 1; (1 << i) <= p + 1; i++) {
int mid = p - (1 << (i - 1));
st[i][p] = min(st[i - 1][p], st[i - 1][mid]);
}
}
// 查询稀疏表,获取区间 [l, r] 的最小值
int query(int l, int r) {
if (l > r) return 0; // 如果区间无效,说明没有前驱红色线段,代价为0
int k = Log2[r - l + 1];
return min(st[k][r], st[k][l + (1 << k) - 1]);
}
int main()
{
int n; scanf("%d", &n);
init(n);
// 设置哨兵
a[0].l = a[0].r = -INF;
maxl[0] = -INF;
for (int i = 1; i <= n; i++) {
scanf("%d%d", &a[i].l, &a[i].r);
}
// 1. 按右端点对所有线段进行排序
sort(a + 1, a + n + 1);
// 2. 预处理前缀最大左端点
for (int i = 1; i <= n; i++) maxl[i] = max(maxl[i - 1], a[i].l);
int ans = INF * 2; // 初始化最终答案为一个极大值
// 3. 动态规划
for (int i = 1; i <= n; i++) {
// --- 计算 dp[i] ---
// dp[i] = (a[i]的长度) + (覆盖a[i]左侧未覆盖部分的最小代价)
// 3.1. 第一次二分:找到 p_i
// 找到满足 a[p].r < a[i].l 的最大索引 p。
// 这个 p 意味着线段 1...p 都不能被 a[i] 覆盖,必须由之前的红色线段解决。
int low = 0, high = i - 1, r_idx = 0;
while (low <= high) {
int mid = low + (high - low) / 2;
if (a[mid].r < a[i].l) {
low = mid + 1;
r_idx = mid;
} else {
high = mid - 1;
}
}
// 3.2. 第二次二分:找到 l_idx
// 在 [0, r_idx] 范围内,寻找一个最小的索引 l,使得从 l 到 r_idx 的所有线段 k
// 都能作为合法的“前一条”红色线段。
// 合法性:a[k] 必须能覆盖所有它需要覆盖的线段。一个简化的条件是 a[k].r >= maxl[r_idx]。
low = 0; high = r_idx;
int l_idx = 0;
while (low <= high) {
int mid = low + (high - low) / 2;
if (a[mid].r >= maxl[r_idx]) {
high = mid - 1;
l_idx = mid;
} else {
low = mid + 1;
}
}
// 3.3. DP 转移
// 在所有合法的候选前驱 k (k in [l_idx, r_idx]) 中,找到最小的 dp[k]。
// dp[i] = (a[i]的长度) + min(dp[k] for k in [l_idx, r_idx])
dp[i] = a[i].r - a[i].l + query(l_idx, r_idx);
// 3.4. 更新 RMQ 结构
// 将新计算出的 dp[i] 加入稀疏表,供后续的计算使用。
update(i, dp[i]);
// 4. 更新最终答案
// 如果 a[i] 作为最右的红色线段,能够覆盖所有 n 条线段,
// (判定条件 a[i].r >= maxl[n]),那么 dp[i] 就是一个候选的全局最优解。
if (a[i].r >= maxl[n]) {
ans = min(ans, dp[i]);
}
}
printf("%d\n", ans);
return 0;
}
习题:CF1889C2 Doremy's Drying Plan (Hard Version)
解题思路
考虑每个点 \(i\),如果我们希望点 \(i\) 不被覆盖,那么需要清空覆盖点 \(i\) 的所有线段。
从左向右依次考虑每个点是否可以不被覆盖,那么在考虑 \(i\) 点之前已经删除了一些线段,这时实际上有一部分覆盖在 \(i\) 上的线段可能会在之前的阶段被考虑删除过,所以决定因素在于上一个不被覆盖的点的位置。

这里得到了一个子问题结构,考虑动态规划。设 \(dp_{i,j}\) 表示考虑前 \(i\) 个点且最后一个不被覆盖的点为 \(i\),当前总共删去 \(j\) 条线段,最多能有多少个点不被覆盖,有转移方程:\(dp_{i,j} = \max \limits_{t=0}^{i-1} \{ dp_{t,j-cost(t,i)} \} + 1\),其中 \(cost(t,i)\) 表示的是满足 \(t < l \le i \le r\) 的线段数量,也就是绿色类型的线段的数量。基于这个状态转移方程,可以得到一个转移时间复杂度为 \(O(n^2 k)\) 的算法,所以需要进一步优化。
如果覆盖在 \(i\) 上面的线段超过了 \(k\) 条,那么 \(i\) 上的覆盖一定无法消除,只考虑 \(i\) 上的覆盖线段数小于等于 \(k\) 的情况,此时 \(cost(t,i) \le k\)。
容易发现当 \(t\) 减小时,\(cost(t,i)\) 会增大,且不会超过 \(k\)。
假设有 \(c\) 条线段覆盖在 \(i\) 上面,将覆盖在 \(i\) 上的线段按左端点从小到大排序,得到左端点序列 \([l_1, l_2, \dots, l_c]\)。这个序列将区间 \([0, i-1]\) 划分成了很多个区间 \([0, l_1-1], [l_1, l_2-1], \dots, [l_c, i-1]\),对于每一段内部而言,它们的 \(cost\) 是相等的。因此这里的每一小段区间内部的 \(dp\) 最大值可以用数据结构优化维护。
将 Sparse Table 倒过来使用,用 \(st_{i,j,len}\) 表示 \(dp\) 状态中第二维取 \(j\) 时第一维以 \(i\) 结尾的 \(2^{len}\) 个数的最大值,就能够动态地在序列末尾以 \(O(\log n)\) 的时间复杂度实现插入操作,以 \(O(1)\) 的时间复杂度完成某个区间的查询。
最终时间复杂度为 \(O(nk^2+nk\log n + m \log m)\)。
参考代码
#include <cstdio>
#include <vector>
#include <set>
#include <algorithm>
using namespace std;
const int N = 200005;
const int K = 15;
const int LOG = 18;
vector<int> left[N], right[N];
int diff[N], cnt[N], st[N][K][LOG], Log2[N];
// st[i][j][len] -> max(dp[i-(1<<len)+1],...,dp[i][j])
multiset<pair<int, int>> s;
int query(int l, int r, int used) {
int len = Log2[r - l + 1];
return max(st[r][used][len], st[l + (1 << len) - 1][used][len]);
}
int main()
{
Log2[1] = 0;
for (int i = 2; i < N; i++) Log2[i] = Log2[i / 2] + 1;
int t; scanf("%d", &t);
while (t--) {
int n, m, k; scanf("%d%d%d", &n, &m, &k);
for (int i = 1; i <= n; i++) {
left[i].clear(); right[i].clear();
diff[i] = 0;
}
for (int i = 1; i <= m; i++) {
int l, r; scanf("%d%d", &l, &r);
left[l].push_back(r); right[r].push_back(l);
diff[l]++; diff[r + 1]--;
}
for (int i = 1; i <= n; i++) cnt[i] = cnt[i - 1] + diff[i];
for (int i = 1; i <= n; i++)
for (int j = 0; j <= k; j++)
for (int len = 0; len < LOG; len++)
st[i][j][len] = 0;
for (int i = 1; i <= n; i++) {
for (int x : left[i]) s.insert({i, x});
for (int j = 0; j <= k; j++) {
if (cnt[i] <= k) {
int prej = j - cnt[i], pre = 0;
for (auto p : s) {
int l = p.first;
// dp[i][j] = max(dp[...][j-cost]) + 1
if (l != pre && j >= cnt[i])
st[i][j][0] = max(st[i][j][0], query(pre, l - 1, prej) + 1);
prej++; pre = l;
}
if (pre != i && j >= cnt[i])
st[i][j][0] = max(st[i][j][0], query(pre, i - 1, prej) + 1);
}
for (int len = 1; (1 << len) <= i + 1; len++) {
int mid = i - (1 << (len - 1));
st[i][j][len] = max(st[i][j][len - 1], st[mid][j][len - 1]);
}
}
for (int x : right[i]) s.erase(s.find({x, i}));
}
int ans = 0;
for (int i = 0; i <= k; i++) ans = max(ans, query(0, n, i));
printf("%d\n", ans);
}
return 0;
}
稀疏表维护其他信息
Sparse Table 不仅可以求区间最大值和最小值,还可以处理符合结合律和幂等律(与自身做运算,结果仍是自身)的信息查询,如区间最大公约数、区间最小公倍数、区间按位或、区间按位与等。
例题:ABC254F Rectangle GCD
有一个 \(N \times N\) 的网格,其中第 \(i\) 行第 \(j\) 列的格子 \((i,j)\) 中的值为 \(A_i+B_j\)。给定 \(Q\) 个查询,每个查询给出一个矩形区域的左上角 \((h_1,w_1)\) 和右下角 \((h_2,w_2)\),要求计算这个矩形区域内所有值的最大公约数(GCD)。
数据范围:
- \(1 \leq N, Q \leq 2 \times 10^5\)
- \(1 \leq A_i, B_i \leq 10^9\)
直接对每个查询遍历矩形内的所有数并计算GCD,时间复杂度过高,无法接受,需要利用GCD的性质来优化计算。
一个关键的性质是 \(\text{gcd}(c_1, c_2, \dots, c_k) = \text{gcd}(c_1, c_2-c_1, c_3-c_1, \dots, c_k-c_1)\)。
对于一个查询的矩形区域,可以选择左上角的点 \((h_1, w_1)\) 作为基准,其值为 \(C_{h_1,w_1} = A_{h_1} + B_{w_1}\)。该区域所有数的 GCD,称之为 \(G\),必须能整除矩形内的每一个数。因此,\(G\) 也必须能整除任意两个数之差。
考虑矩形内任意一点 \((i, j)\) 与基准点 \((h_1, w_1)\) 的差:
\(C_{i,j} - C_{h_1,w_1} = (A_i + B_j) - (A_{h_1} + B_{w_1}) = (A_i - A_{h_1}) + (B_j - B_{w_1})\)
\(G\) 必须能整除所有这些差值。
- 特别地,当 \(j=w_1\) 时,差值为 \(A_i - A_{h_1}\)。所以 \(G\) 必须整除所有 \(A_i - A_{h_1}\)(对于 \(h_1 \le i \le h_2\))。
- 同理,当 \(i=h_1\) 时,差值为 \(B_j - B_{w_1}\)。所以 \(G\) 必须整除所有 \(B_j - B_{w_1}\)(对于 \(w_1 \le j \le w_2\))。
因此,\(G\) 必须整除 \(\gcd\limits_{i=h_1+1}^{h_2}(A_i - A_{h_1})\) 和 \(\gcd\limits_{j=w_1+1}^{w_2}(B_j - B_{w_1})\)。
可以进一步利用GCD性质 \(\text{gcd}(d_1, d_2, \dots) = \text{gcd}(d_1, d_2-d_1, d_3-d_2, \dots)\) 来简化差值的 GCD 计算,
\(\gcd\limits_{i=h_1+1}^{h_2}(A_i - A_{h_1})\) 可以被展开为 \(\text{gcd}(A_{h_1+1}-A_{h_1}, A_{h_1+2}-A_{h_1}, \dots)\),
这等价于 \(\text{gcd}(A_{h_1+1}-A_{h_1}, A_{h_1+2}-A_{h_1+1}, \dots, A_{h_2}-A_{h_2-1})\)。
换句话说,一组数与同一个数的差值的 GCD,等于这组数相邻元素之差的 GCD。
所以,\(\gcd\limits_{i=h_1+1}^{h_2}(A_i - A_{h_1}) = \gcd\limits_{i=h_1}^{h_2-1}(A_{i+1} - A_i)\)。
综上所述,矩形区域的 GCD 可以表示为:
\(G = \text{gcd}(A_{h_1} + B_{w_1}, \quad \gcd\limits_{i=h_1}^{h_2-1}|A_{i+1} - A_i|, \quad \gcd\limits_{j=w_1}^{w_2-1}|B_{j+1} - B_j|)\)
(对差值取绝对值,因为 GCD 通常在非负整数上定义)
问题被转化为了三个部分的GCD:
- 左上角的值 \(A_{h_1} + B_{w_1}\)。
- 数组 \(A\) 的相邻差值数组在区间 \([h_1, h_2-1]\) 上的区间 GCD。
- 数组 \(B\) 的相邻差值数组在区间 \([w_1, w_2-1]\) 上的区间 GCD。
对于区间 GCD 查询,稀疏表是一个理想的数据结构。它可以在 \(O(N \log N)\) 的预处理后,以 \(O(1)\) 的时间复杂度回答每个查询。
参考代码
#include <iostream>
#include <vector>
#include <cmath>
#include <algorithm>
using namespace std;
using ll = long long;
// 欧几里得算法计算最大公约数 (Greatest Common Divisor)
ll gcd(ll a, ll b) {
return b == 0 ? a : gcd(b, a % b);
}
const int N = 200005;
const int LOG = 18;
// 稀疏表 (Sparse Table) 结构体,用于 O(1) 回答区间GCD查询
struct SparseTable {
ll st[N][LOG]; // 存储预计算的GCD值
int log_table[N]; // 存储 log2 的整数部分,用于快速计算
// 构建稀疏表
// 时间复杂度: O(n log n)
void build(const vector<ll>& arr, int n) {
if (n == 0) return;
// 预计算 log2(i) 的值,加速查询
log_table[1] = 0;
for (int i = 2; i <= n; i++) {
log_table[i] = log_table[i / 2] + 1;
}
// 初始化稀疏表的第一列 (即长度为 2^0=1 的区间)
for (int i = 0; i < n; i++) {
st[i][0] = arr[i];
}
// 动态规划填充整个稀疏表
// st[i][k] 表示从索引 i 开始,长度为 2^k 的区间的GCD
for (int k = 1; k < LOG; k++) {
for (int i = 0; i + (1 << k) <= n; i++) {
st[i][k] = gcd(st[i][k - 1], st[i + (1 << (k - 1))][k - 1]);
}
}
}
// 查询区间 [l, r] (0-indexed) 的GCD
// 时间复杂度: O(1)
ll query(int l, int r) {
if (l > r) return 0; // 空区间的GCD为0,不影响最终结果
int k = log_table[r - l + 1];
// 查询的区间可以被两个长度为 2^k 的子区间覆盖
return gcd(st[l][k], st[r - (1 << k) + 1][k]);
}
};
int n, q;
vector<ll> a, b, da, db;
SparseTable sta, stb;
int main() {
scanf("%d%d", &n, &q);
a.resize(n);
b.resize(n);
for (int i = 0; i < n; i++) scanf("%lld", &a[i]);
for (int i = 0; i < n; i++) scanf("%lld", &b[i]);
// 预处理步骤:创建差值数组并构建稀疏表
if (n > 1) {
da.resize(n - 1);
db.resize(n - 1);
for (int i = 0; i < n - 1; i++) {
da[i] = abs(a[i + 1] - a[i]);
db[i] = abs(b[i + 1] - b[i]);
}
sta.build(da, n - 1);
stb.build(db, n - 1);
}
for (int i = 0; i < q; i++) {
int h1, h2, w1, w2;
scanf("%d%d%d%d", &h1, &h2, &w1, &w2);
// 将1-based的输入坐标转换为0-based的数组索引
h1--; h2--; w1--; w2--;
// 根据推导出的公式计算结果:
// gcd(A[h1]+B[w1], range_gcd(dA, h1, h2-1), range_gcd(dB, w1, w2-1))
// 初始答案为矩形左上角的值
ll ans = a[h1] + b[w1];
// 如果矩形不止一行,则需要考虑行之间的差值GCD
if (h1 < h2) {
ans = gcd(ans, sta.query(h1, h2 - 1));
}
// 如果矩形不止一列,则需要考虑列之间的差值GCD
if (w1 < w2) {
ans = gcd(ans, stb.query(w1, w2 - 1));
}
printf("%lld\n", ans);
}
return 0;
}
习题:P14577 磁极变换
解题思路
首先,分析磁铁的消除规则。对于任意一种材料(字符)\(c\),在指定的区间 \([l,r]\) 内,其第 1、3、5、……次出现会与第 2、4、6、……次出现配对。例如,第 1 个 \(c\) 和第 2 个 \(c\) 配对,第 3 个 \(c\) 和第 4 个 \(c\) 配对,以此类推。每一对磁铁相撞,会消灭它们自身以及它们之间的所有磁铁。
这个规则有两个关键推论:
- 配对消除:对于一种材料 \(c\),只有当它在区间 \([l,r]\) 内出现了奇数次时,才会有一个 \(c\) 因为找不到配对对象而剩下来。这个剩下的,必然是最后一次出现的那个。
- 幸存可能:因此,对于整个区间 \([l,r]\),最终能幸存下来的磁铁,必然是那些在 \([l,r]\) 中出现奇数次的材料的最后一次出现,称这些磁铁为候选幸存者。
一个候选幸存者就一定能最终幸存吗?
不一定,因为它虽然没有在同类磁铁的碰撞中被消灭,但它可能被其他种类磁铁的碰撞“波及”而被消灭。
一个位于 \(p\) 位置、材料为 \(c\) 的候选幸存者,会被消灭的充要条件是,存在另一种材料 \(d\),它在 \([l,r]\) 内的某一对碰撞 \((p_1,p_2)\) 满足 \(p_1 \lt p \lt p_2\)。
这个条件看起来仍然很复杂,需要遍历所有其他材料的配对,但可以进一步转化它。
一个 \(d\) 材料的碰撞区间 \([p_1, p_2]\) 能够“跨过” \(p\),意味着 \(p_1\) 是 \(d\) 的第 \(2k-1\) 次出现,\(p_2\) 是第 \(2k\) 次出现。这隐含着在 \(p_1\) 之前,\(d\) 出现了偶数次。换言之,\(d\) 在区间 \([l,p_1-1]\) 中出现了偶数次。
可以得到一个更简洁的等价条件,位置 \(p\) 的候选幸存者会被消灭,当且仅当存在一种材料 \(d\),它同时满足:
- 在 \(p\) 的左侧区间 \([l,p-1]\) 内,\(d\) 出现了奇数次。(这留下了一个未配对的 \(d\))
- 在 \(p\) 的右侧区间 \([p+1,r]\) 内,\(d\) 至少出现了一次。(这个 \(d\) 可以与左侧那个未配对的 \(d\) 形成跨越 \(p\) 的碰撞)
因此,一个候选幸存者能够最终幸存的条件是,对于所有其他材料 \(d\),上述条件都不成立。
直接根据上述条件进行查询,复杂度依然很高。需要用空间换时间,通过预处理加速查询。
可以用一个 26 位的二进制数来表示字符集情况,针对条件 1,可以利用前缀异或和预处理前缀出现字符的奇偶性情况,针对条件 2,可以预处理稀疏表来存储区间中所有出现过的字符的位掩码(用或运算合并)。
参考代码
#include <cstdio>
// --- 题解思路 ---
// 1. 分析幸存者:
// - 对于任意一种字符 c,在区间 [l, r] 内,第1和2个、第3和4个... c 会配对并消亡。
// - 因此,只有当 c 在 [l, r] 中出现奇数次时,其最后一次出现的那块磁铁才有可能幸存,称之为“候选幸存者”。
// - 一个候选幸存者最终能否幸存,取决于它是否被其他种类磁铁的配对碰撞所波及。
//
// 2. 判断是否被波及:
// - 假设字符 i 的候选幸存者在位置 pos。
// - 它会被消灭,当且仅当存在另一种字符 j,它在 [l, r] 中的第 2k-1 次和第 2k 次出现的位置 p1, p2 满足 p1 < pos < p2。
// - 这个条件等价于:在 [l, pos-1] 区间内,字符 j 出现了奇数次(留下了一个未配对的),同时在 [pos+1, r] 区间内,字符 j 至少出现了一次(可以与之配对)。
//
// 3. 高效实现:
// - 前缀异或和 pre:pre[i] 存储 s[1...i] 中各字符出现次数奇偶性的 bitmask。通过 pre[y] ^ pre[x-1] 可以在 O(1) 内得到 [x, y] 区间的奇偶性 bitmask。这能快速找到候选幸存者,并判断条件2中的“奇数次”。
// - last 数组:last[i][c] 存储字符 c 在 s[1...i] 中最后一次出现的位置。这能 O(1) 找到候选幸存者的具体位置 pos。
// - 稀疏表:用于在 O(1) 内查询 [l, r] 区间内存在哪些字符。这能快速判断条件2中的“至少出现一次”。
//
// 4. 查询流程 (2 l r):
// a. 计算 mask = pre[r] ^ pre[l-1],得到 [l,r] 内出现奇数次的字符集合。
// b. 遍历所有字符 i (0-25):
// - 如果 i 在 mask 中(即出现奇数次),它就是一个候选。
// - 找到它的位置 pos = last[r][i]。
// - 计算 [l, pos-1] 区间的奇偶性 left_mask = pre[pos-1] ^ pre[l-1]。
// - 查询 [pos+1, r] 区间存在的字符 right_mask = query(pos+1, r)。
// - 如果 (left_mask & right_mask) == 0,说明没有任何字符 j 同时满足“左边奇数个”和“右边存在”,因此 pos 不会被波及,是真正的幸存者。将其价值 a[pos] 加入答案。
using ll = long long;
const int N = 5e5 + 5;
const int LOG = 19;
char s[N];
int pre[N], a[N], last[N][26];
int Log2[N], st[LOG][N];
/**
* @brief 初始化稀疏表 (ST Table)
* 用于 O(1) 查询区间内出现过的所有字符的 bitmask。
*/
void init(int n) {
Log2[1] = 0;
for (int i = 2; i <= n; i++) Log2[i] = Log2[i / 2] + 1;
for (int i = 1; i <= n; i++) {
st[0][i] = (1 << (s[i] - 'a'));
}
for (int i = 1; i < LOG; i++) {
for (int j = 1; j <= n - (1 << i) + 1; j++) {
st[i][j] = st[i - 1][j] | st[i - 1][j + (1 << (i - 1))];
}
}
}
/**
* @brief 查询 [l, r] 区间内所有出现过的字符的 bitmask。
*/
int query(int l, int r) {
if (l > r) return 0;
int k = Log2[r - l + 1];
return st[k][l] | st[k][r - (1 << k) + 1];
}
int main()
{
int n;
scanf("%d%s", &n, s + 1);
init(n); // 初始化ST表
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]);
}
// --- 预处理 ---
pre[0] = 0;
for (int i = 1; i <= n; i++) {
// 计算前缀异或和
pre[i] = pre[i - 1] ^ (1 << (s[i] - 'a'));
// 继承上一个位置的 last 信息
for (int j = 0; j < 26; j++) {
last[i][j] = last[i - 1][j];
}
// 更新当前字符的 last 位置
last[i][s[i] - 'a'] = i;
}
int q;
scanf("%d", &q);
while (q--) {
int op, x, y;
scanf("%d%d%d", &op, &x, &y);
if (op == 1) {
// 更新价值是 O(1) 操作
a[x] = y;
} else {
ll ans = 0;
// 1. 找到所有在 [x, y] 区间出现奇数次的字符,它们是候选幸存者
int mask = pre[y] ^ pre[x - 1];
for (int i = 0; i < 26; i++) {
// 如果字符 i 出现偶数次,跳过
if (!((mask >> i) & 1)) continue;
// 2. 找到候选幸存者的位置(即该字符在 [x, y] 中最后一次出现的位置)
int pos = last[y][i];
// 3. 判断该幸存者是否会被其他字符的碰撞波及
// 计算 [x, pos-1] 区间内出现奇数次的字符集合
int left = pre[pos - 1] ^ pre[x - 1];
// 查询 [pos+1, y] 区间内出现过的字符集合
int right_chars = query(pos + 1, y);
// left & right_chars 不为0,意味着存在一个字符 j,
// 它在 pos 左边有奇数个,在 pos 右边也存在。
// 这会导致 j 的一个配对碰撞区间跨过 pos,从而消灭 pos。
if(!(left & right_chars)) {
// 如果没有这样的字符,则 pos 处的磁铁幸存
ans += a[pos];
}
}
printf("%lld\n", ans);
}
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号