单调栈
单调栈是一种内部元素具有单调性的栈，可以解决与“以某个值为最值的最大区间”等问题。
对于一个数组 \(a\)，找到每个元素前边/后边第一个比它大/小的元素。假如数组中某个元素后边第一个比它大的是 \(a_r\)，前边第一个比它大的是 \(a_l\)，则 \([l+1, r-1]\) 这个区间内的最大值是这个元素。推广到左端点在 \([l+1,i]\)，右端点在 \([i, r-1]\)，这样的区间的最大值都是 \(a_i\)。
考虑单调队列维护区间最大值的过程：当 \(a_i\) 大于队尾时，队尾出队，这个时候一定是队尾第一次碰到右边比它大的元素（记录被弹出来的时候）。由于从来没做过队首出队的操作，所以单调栈可以看成永远不会出队首的单调队列。对称地，倒序循环，就能知道左边第一个比它大的（记录被弹出来的时候）。
while (!s.empty() && a[i] > a[s.top()]) {
r[s.top()] = i; s.pop();
}
s.push(i);
例如 \(a = [1, 4, 2, 3, 5]\)，走到第 \(4\) 位这个 \(3\)。以找第一个最大值为例，单调栈维护的元素是递减的，每次先淘汰栈顶比当前元素小的，剩下的栈顶比当前元素大，然后当前元素进栈（\([a_1] \rightarrow [a_2] \rightarrow [a_2, a_3] \rightarrow [a_2, a_4]\)）。可以看到：区间 \([1,4]\) 的最大值是 \(4\)，区间 \([2,4]\) 的最大值是 \(4\)，区间 \([3,4]\) 的最大值是 \(3\)，区间 \([4,4]\) 的最大值是 \(3\)，……。
例题：P2866 [USACO06NOV] Bad Hair Day S
有 \(N \ (1 \le N \le 80000)\) 头奶牛，第 \(i\) 头牛的身高为 \(h_i \ (1 \le h_i \le 10^9)\)。每只奶牛往右边看，可以看到严格小于它身高的牛的头顶，直到看到了身高不小于它的牛（看不到这头牛的头顶），或者右边没有其他奶牛为止。第 \(i\) 头牛可以看到的头顶数量为 \(C_i\)，求 \(\sum_{i=1}^n C_i\)。假设有 \(6\) 头牛，高度分别为 \(10,3,7,4,12,2\)，那么它们分别可以看到 \(3,0,1,0,1,0\) 头牛的头发，其总和为 \(5\)。
分析：如果使用暴力枚举求解，对于每一头牛都往右边枚举身高小于它的牛，那么时间复杂度是 \(O(n^2)\) 的，无法通过本题。
可以转变一下思路，求每头牛能看见几头牛，等价于计算每头牛能被多少其他牛看见。一头牛能被哪些牛看见？左边比它高的牛，再左边比它高的牛，……。可以维护一个序列，满足这个序列里存的都是对于第 \(i\) 头牛来说，其左边的身高比它高的牛的身高（这会是一个单调递减的序列），可以使用栈来进行维护。
最开始栈是空的。身高为 \(10\) 的牛进栈，原来栈里没有牛，那么答案增加 \(0\)；身高为 \(3\) 的牛来了，则需要从栈顶开始，把所有小于等于 \(3\) 的牛都出栈，此时左边剩 \(1\) 头牛，答案增加 \(1\)，然后再将其入栈；身高为 \(7\) 的牛来了，从栈顶开始，把所有小于等于 \(7\) 的牛都出栈（比如刚才入栈的 \(3\) 就要出栈），此时左边有 \(1\) 头牛，答案增加 \(1\)，然后再将其入栈，……，以此类推。
像这样维护一个值单调递减（或者递增）的数据结构，称为单调栈。
参考代码
#include <cstdio>
#include <stack>
using std::stack;
using ll = long long;
const int N = 80005;
int h[N];
int main()
{
int n; scanf("%d", &n);
for (int i = 1; i <= n; i++) scanf("%d", &h[i]);
stack<int> s;
ll ans = 0; // 极端情况下，答案是n的平方级别，超过了int范围，需要long long类型
for (int i = 1; i <= n; i++) {
while (!s.empty() && s.top() <= h[i]) s.pop();
ans += s.size();
s.push(h[i]);
}
printf("%lld\n", ans);
return 0;
}
在本题中，单调栈能以 \(O(n)\) 的时间复杂度找到每一个元素右边第一个比它大的数字（就是把这个数字挤出栈的数字），如果设 \(r_i\) 表示 \(h_i\) 右侧第一个大于等于 \(h_i\) 的位置，实际上本题就是在求 \(\sum_{i=1}^n (r_i - i - 1)\)。
参考代码
#include <cstdio>
#include <stack>
using std::stack;
using ll = long long;
const int N = 80005;
int h[N], r[N];
int main()
{
int n; scanf("%d", &n);
for (int i = 1; i <= n; i++) scanf("%d", &h[i]);
stack<int> s; // 栈中存储的是元素的下标
for (int i = 1; i <= n; i++) {
while (!s.empty() && h[i] >= h[s.top()]) {
r[s.top()] = i; s.pop();
}
s.push(i);
}
while (!s.empty()) { // 注意栈中剩余的元素代表其右侧没有大于等于它的元素
r[s.top()] = n + 1; s.pop();
}
ll ans = 0; // 极端情况下，答案是n的平方级别，超过了int范围，需要long long类型
for (int i = 1; i <= n; i++) ans += r[i] - i - 1;
printf("%lld\n", ans);
return 0;
}
例题：P8094 [USACO22JAN] Cow Frisbee S
这是一个非常巧妙的单调栈应用，首先，分析题目给出的条件：\(\max(h_{i+1}, h_{i+2}, \dots, h_{j-1}) \lt \min(h_i, h_j)\)，这个条件意味着 \(i\) 和 \(j\) 之间没有“高个子”阻挡。
关键的等价转化：可以证明，满足上述条件的配对 \((i,j)\)，当且仅当它们是彼此的“下一个更高元素”之一。也就是说，一个配对 \((i,j)\)（设 \(i \lt j\)）合法，当且仅当满足以下两个条件之一：
- \(h_j\) 是位置 \(i\) 右侧第一个比 \(h_i\) 高的奶牛。
- \(h_i\) 是位置 \(j\) 左侧第一个比 \(h_j\) 高的奶牛。
这个转化将问题变为了一个经典的“寻找下一个/上一个更大元素”的问题，正是单调栈的用武之地。目标是找到所有这样的配对，并计算其距离和。
单调栈一次遍历解法：通常，可以用两次遍历（一次从左到右，一次从右到左）来分别求每个元素的“下一个更高”和“上一个更高”，但本题可以通过一次精巧的从左到右的遍历来找到所有配对。
维护一个高度单调递减的栈，栈中存放元素的索引，当遍历到第 \(i\) 个元素 \(h_i\) 时：
- 出栈判断：不断比较 \(h_i\) 和栈顶元素对应的高度，如果 \(h_i\) 更大，说明当前的 \(h_i\) 是栈顶元素右侧遇到的第一个比它更高的元素。因此，栈顶和 \(i\) 构成一个合法的飞盘对。将两者的距离累加到答案中，然后将栈顶元素弹出。重复此过程，直到栈顶元素不小于 \(h_i\) 或栈为空。
- 入栈判断：经过步骤 1 后，如果栈不为空，那么现在的栈顶元素一定大于 \(h_i\)（因为题中身高是排列，不会相等）。并且，这个栈顶元素是 \(i\) 左侧遇到的第一个比它高的元素。因此，此时的栈顶和 \(i\) 也构成一个合法的飞盘对，将距离累加到答案中。
- 入栈：将当前索引 \(i\) 压入栈中，以维持栈的单调递减性。
通过这样一次遍历，每个合法的配对都会被恰好计算一次。例如，配对 \((i,j)\)（其中 \(h_i \lt h_j\)）会在遍历到 \(j\) 时，当 \(i\) 被从栈中弹出时被计算。而配对 \((i,j)\)（其中 \(h_i \gt h_j\)）会在遍历到 \(j\) 时，当 \(i\) 作为新的栈顶时被计算。
整个算法每个元素入栈、出栈各一次，时间复杂度为 \(O(N)\)。
参考代码
#include <cstdio>
#include <vector>
#include <stack>
using ll = long long;
using namespace std;
int main() {
int n;
scanf("%d", &n);
vector<int> h(n);
for (int i = 0; i < n; ++i) {
scanf("%d", &h[i]);
}
ll ans = 0;
stack<int> s; // 单调栈，存储索引，对应的高度单调递减
// 从左到右遍历
for (int i = 0; i < n; ++i) {
// 维护一个高度单调递减的栈
// 当遇到新的奶牛 h[i] 时，它比栈顶的奶牛高
while (!s.empty() && h[s.top()] < h[i]) {
// 栈顶奶牛 j 被 h[i] "看见"
// i 是 j 右侧第一个比 j 高的奶牛
int j = s.top();
s.pop();
// 形成飞盘对 (j, i)，累加距离
ans += (i - j + 1);
}
// 此时，如果栈不为空，栈顶奶牛 k 比 h[i] 高
// k 是 i 左侧第一个比 i 高的奶牛
if (!s.empty()) {
// 形成飞盘对 (s.top(), i)，累加距离
ans += (i - s.top() + 1);
}
// 将当前奶牛的索引压入栈
s.push(i);
}
printf("%lld\n", ans);
return 0;
}
例题：SP1805 HISTOGRA - Largest Rectangle in a Histogram
如果矩形的高度从左到右递增，那么答案是多少？显而易见，可以尝试以每个矩形的高度作为最终矩形的高度，并把宽度延伸到右边界，得到一个矩形，在所有这样的矩形面积中取最大值就是答案。
受这种思路启发，如果能够知道以每一个高度的矩形作为最终矩形的高度向左、向右最多能延伸到哪，则这一段之间的就是最终矩形的宽度，在所有这样的矩形面积中取最大的。而向左、向右最多能延伸到哪实际上就是找每个高度的左边、右边第一个高度低于自己的位置。这一点可以通过单调栈实现。
参考代码
#include <cstdio>
#include <stack>
#include <algorithm>
using std::max;
using std::stack;
using ll = long long;
const int N = 100005;
int h[N], l[N], r[N];
int main()
{
while (true) {
int n; scanf("%d", &n);
if (n == 0) break;
for (int i = 1; i <= n; i++) scanf("%d", &h[i]);
stack<int> s;
for (int i = 1; i <= n; i++) {
while (!s.empty() && h[s.top()] > h[i]) {
r[s.top()] = i; s.pop();
}
s.push(i);
}
while (!s.empty()) {
r[s.top()] = n + 1; s.pop();
}
for (int i = n; i >= 1; i--) {
while (!s.empty() && h[s.top()] > h[i]) {
l[s.top()] = i; s.pop();
}
s.push(i);
}
while (!s.empty()) {
l[s.top()] = 0; s.pop();
}
ll ans = 0;
for (int i = 1; i <= n; i++) {
ans = max(ans, 1ll * h[i] * (r[i] - l[i] - 1));
}
printf("%lld\n", ans);
}
return 0;
}
习题：P5788 【模板】单调栈
参考代码
#include <cstdio>
#include <stack>
using std::stack;
const int N = 3000005;
int a[N], f[N];
int main()
{
int n; scanf("%d", &n);
for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
stack<int> s;
for (int i = 1; i <= n; i++) {
while (!s.empty() && a[i] > a[s.top()]) {
f[s.top()] = i; s.pop();
}
s.push(i);
}
for (int i = 1; i <= n; i++) printf("%d ", f[i]);
return 0;
}
习题：P2947 [USACO09MAR] Look Up S
参考代码
#include <cstdio>
#include <stack>
using std::stack;
const int N = 100005;
int h[N], ans[N];
int main()
{
int n; scanf("%d", &n);
for (int i = 1; i <= n; i++) scanf("%d", &h[i]);
stack<int> s;
for (int i = 1; i <= n; i++) {
while (!s.empty() && h[i] > h[s.top()]) {
ans[s.top()] = i; s.pop();
}
s.push(i);
}
for (int i = 1; i <= n; i++) printf("%d\n", ans[i]);
return 0;
}
习题：P1106 删数问题
解题思路
依次考虑每一次删除。假如 175438 删一个数，结果必然是一个五位数，当删除某一个数位时相当于找了一个更小的数来做高位，所以应该删除那些下一位数值比当前位小的位，而删除 7 比删除 5 要更好，因为 7 是更高的数位。接下来的每一次删除都是同样的方式。
因此需要保留的数位实际上应该是单调不降的，这可以用单调栈来维护。
用单调栈维护单调不降的数位，当栈顶大于当前处理的数位时相当于就是要删除栈顶对应的数位，输入的 \(k\) 限制了出栈次数。
如果最后出栈次数没有用完，则删除最后几位直到用完所有出栈次数。
注意输出时去除前导 \(0\) 以及特别注意答案就是 \(0\) 的情况。
参考代码
#include <cstdio>
#include <cstring>
#include <stack>
using std::stack;
const int LEN = 255;
char num[LEN], ans[LEN];
int main()
{
int k;
scanf("%s%d", num + 1, &k);
int len = strlen(num + 1);
stack<char> s;
for (int i = 1; i <= len; i++) {
while (!s.empty() && k > 0 && num[i] < s.top()) {
k--; s.pop();
}
s.push(num[i]);
}
while (!s.empty() && k > 0) {
k--; s.pop();
}
// 注意本题要求输出的结果中去掉前导0
int idx = 0;
while (!s.empty()) {
ans[++idx] = s.top(); s.pop();
}
while (idx > 1 && ans[idx] == '0') idx--;
for (int i = idx; i >= 1; i--) printf("%c", ans[i]);
return 0;
}
习题：P1901 发射站
解题思路
根据题意，“一个发射站发出的能量被两边最近的且比它高的发射站接收”，所以就是要求出每一个发射站左边/右边第一个更高的发射站的位置，进而将发射站的能量累加上去，最后找出接收能量最多的发射站。
参考代码
#include <cstdio>
#include <stack>
#include <algorithm>
using std::stack;
using std::max;
const int N = 1000005;
int h[N], v[N], l[N], r[N], power[N];
int main()
{
int n; scanf("%d", &n);
for (int i = 1; i <= n; i++) scanf("%d%d", &h[i], &v[i]);
stack<int> s;
// 求出每个发射站右边第一个更高的发射站位置
for (int i = 1; i <= n; i++) {
while (!s.empty() && h[i] > h[s.top()]) {
r[s.top()] = i; s.pop();
}
s.push(i);
}
while (!s.empty()) s.pop();
// 求出每个发射站左边第一个更高的发射站位置
for (int i = n; i >= 1; i--) {
while (!s.empty() && h[i] > h[s.top()]) {
l[s.top()] = i; s.pop();
}
s.push(i);
}
// 更新每个发射站接收到的能量
for (int i = 1; i <= n; i++) {
if (l[i] > 0) power[l[i]] += v[i];
if (r[i] > 0) power[r[i]] += v[i];
}
int ans = 0;
// 找出接收最多能量的发射站接收到的能量值
for (int i = 1; i <= n; i++) ans = max(ans, power[i]);
printf("%d\n", ans);
return 0;
}
例题：P4147 玉蟾宫
有一个 \(N \times M \ (1 \le N,M \le 1000)\) 的矩阵，每个格子里写着
R或者F。找出其中的一个子矩阵，其元素均为F并且面积最大。输出它的面积乘以 \(3\)。
解题思路
预处理出每一个格子所处位置向上最多连续的 F 格子的高度，则相当于沿着每一行计算 SP1805 HISTOGRA - Largest Rectangle in a Histogram。
如何预处理？设 \(h_{i,j}\) 表示第 \(i\) 行第 \(j\) 列的格子向上所能延伸的连续 F 格子高度，则当该格子是 R 时，\(h_{i,j} = 0\)，当该格子是土地时，\(h_{i,j} = h_{i-1,j} + 1\)。
对每一行做一遍单调栈，对这一行的每个格子，求出对应的左右边界。扫一遍单调栈以后，最后还在栈里的，就是没有能淘汰它的。针对这种情况，可以设成边界，从右往左的时候可以认为被下标为 \(0\) 的淘汰，从左往右的时候可以认为被下标为 \(m+1\) 的淘汰。
每一行计算的时间复杂度为 \(O(m)\)，因此总的时间复杂度为 \(O(nm)\)。
参考代码
#include <cstdio>
#include <stack>
#include <algorithm>
using std::stack;
using std::max;
const int N = 1005;
char f[5];
int a[N][N], l[N], r[N];
int main()
{
int n, m; scanf("%d%d", &n, &m);
int ans = 0;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
scanf("%s", f);
a[i][j] = f[0] == 'R' ? 0 : a[i - 1][j] + 1;
}
stack<int> s;
for (int j = 1; j <= m; j++) {
while (!s.empty() && a[i][j] < a[i][s.top()]) {
r[s.top()] = j; s.pop();
}
s.push(j);
}
while (!s.empty()) {
r[s.top()] = m + 1; s.pop();
}
for (int j = m; j >= 1; j--) {
while (!s.empty() && a[i][j] < a[i][s.top()]) {
l[s.top()] = j; s.pop();
}
s.push(j);
}
while (!s.empty()) {
l[s.top()] = 0; s.pop();
}
for (int j = 1; j <= m; j++) {
ans = max(ans, a[i][j] * (r[j] - l[j] - 1));
}
}
printf("%d\n", ans * 3);
return 0;
}
例题：P2422 良好的感觉
找到一个区间使得 区间和 乘 区间最小值 最大，\(n \le 10^5\)。
解题思路
枚举每一位 \(a_i\) 当区间最小值，用单调栈找到 \(a_i\) 作为最小值的左右边界。
参考代码
#include <cstdio>
#include <algorithm>
#include <stack>
using std::max;
using std::stack;
using ll = long long;
const int N = 100005;
int a[N], l[N], r[N];
ll sum[N];
int main()
{
int n; scanf("%d", &n);
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]); sum[i] = sum[i - 1] + a[i];
}
stack<int> s;
for (int i = 1; i <= n; i++) {
while (!s.empty() && a[i] < a[s.top()]) {
r[s.top()] = i; s.pop();
}
s.push(i);
}
while (!s.empty()) {
r[s.top()] = n + 1; s.pop();
}
for (int i = n; i >= 1; i--) {
while (!s.empty() && a[i] < a[s.top()]) {
l[s.top()] = i; s.pop();
}
s.push(i);
}
while (!s.empty()) {
l[s.top()] = 0; s.pop();
}
ll ans = 0;
for (int i = 1; i <= n; i++) {
ans = max(ans, (sum[r[i] - 1] - sum[l[i]]) * a[i]);
}
printf("%lld\n", ans);
return 0;
}
例题：P1950 长方形
小明今天突发奇想，想从一张用过的纸中剪出一个长方形。
为了简化问题，小明做出如下规定：
（1）这张纸的长宽分别为 \(n,m\)。小明将这张纸看成是由\(n \times m\)个格子组成，在剪的时候，只能沿着格子的边缘剪。
（2）这张纸有些地方小明以前在上面画过，剪出来的长方形不能含有以前画过的地方。
（3）剪出来的长方形的大小没有限制。
小明看着这张纸，想了好多种剪的方法，可是到底有几种呢？小明数不过来，你能帮帮他吗？输入格式
第一行两个正整数 \(n,m\)，表示这张纸的长度和宽度。
接下来有 \(n\) 行，每行 \(m\) 个字符，每个字符为*或者.。
字符*表示以前在这个格子上画过，字符.表示以前在这个格子上没画过。输出格式
仅一个整数，表示方案数。
样例输入
6 4 .... .*** .*.. .*** ...* .***样例输出
38数据规模
对 \(10\%\) 的数据，满足 \(1\leq n\leq 10,1\leq m\leq 10\)
对 \(30\%\) 的数据，满足 \(1\leq n\leq 50,1\leq m\leq 50\)
对 \(100\%\) 的数据，满足 \(1\leq n\leq 1000,1\leq m\leq 1000\)
分析：本题可以通过枚举矩形的四条边，然后判断里面是否全是没有画过的部分，但这样时间复杂度很高，所以需要优化效率。
以行为单位处理，统计以每一行为底边的句型数量。举个例子，假设目前在统计第 \(4\) 行。
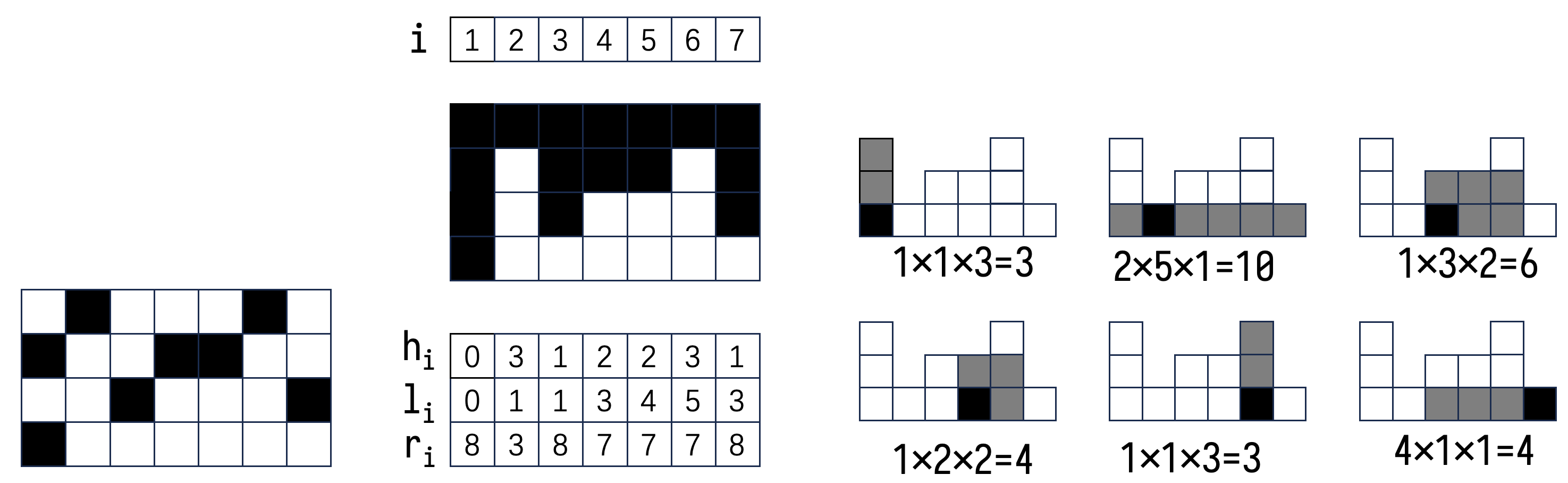
令 \(h_i\) 表示第 \(i\) 列从底往上延伸空格子的数量，\(l_i\) 表示这一列左边第一个满足 \(h\) 值小于等于 \(h_i\) 的列号（如果没有的话就是 \(0\)），\(r_i\) 表示这一列右边第一个满足 \(h\) 值小于 \(h_i\) 的列号（如果没有的话就是 \(m+1\)）。
根据乘法原理，包括这一列最底下的小格子，同时又被这一列的高度限制的长方形的数量是 \((i - l_i) \times (r_i - i) \times h_i\)。为什么 \(l\) 和 \(r\) 的计算一个带等号另一个不带等号，因为这样计数才不会重复不会遗漏（思考为什么？）。每一行都用这种方式处理，然后将每一行的结果汇总就得到了整个问题的结果。
\(h_i\) 如何计算？如果这个格子是画过的格子，则 \(h_i = 0\)，否则 \(h_i\) 的值就是同一列上一行的 \(h_i\) 的值再加 \(1\)。
如何求得 \(l_i\) 和 \(r_i\) 呢？使用单调栈。求 \(r_i\) 需要找到严格小于的，那么判断是否将栈顶元素挤出时，如果待处理的元素等于栈顶元素时不必出栈，只有遇到更小的才会被挤出来，满足栈是单调不减的；而求 \(l_i\) 需要找到小于等于的，则从后往前计算，判断是否将栈顶元素挤出时，如果这个元素小于等于栈顶元素，那么栈顶元素就会被挤出，满足栈是单调递增的。
参考代码
#include <cstdio>
#include <stack>
using std::stack;
using ll = long long;
const int N = 1005;
char ch[N][N];
int h[N][N], l[N], r[N];
int main()
{
int n, m; scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) {
scanf("%s", ch[i] + 1);
for (int j = 1; j <= m; j++) {
h[i][j] = ch[i][j] == '*' ? 0 : h[i - 1][j] + 1;
}
}
ll ans = 0; // 需要考虑极端情况：n=m=1000，而且全是没画过的格子，长方形的数量是n的4次方数量级
for (int i = 1; i <= n; i++) {
// 为了方便在出栈时求出每个元素左边和右边的符合要求的位置
// 栈里实际存储的是下标而不是元素本身
stack<int> s;
// 顺着求右边第一个小于这个数的位置
for (int j = 1; j <= m; j++) {
while (!s.empty() && h[i][s.top()] > h[i][j]) {
r[s.top()] = j; s.pop();
}
s.push(j);
}
while (!s.empty()) {
r[s.top()] = m + 1; s.pop();
}
// 倒着求左边第一个小于等于这个数的位置
for (int j = m; j >= 1; j--) {
while (!s.empty() && h[i][s.top()] >= h[i][j]) {
l[s.top()] = j; s.pop();
}
s.push(j);
}
while (!s.empty()) {
l[s.top()] = 0; s.pop();
}
for (int j = 1; j <= m; j++) {
ans += 1ll * h[i][j] * (j - l[j]) * (r[j] - j);
}
}
printf("%lld\n", ans);
return 0;
}
习题：CF1313C2 Skyscrapers (hard version)
解题思路
枚举哪一栋作为最高的摩天大楼，假设位置 \(i\) 的楼是最高楼，则其建设高度为其限高 \(m_i\)，那么其左边的楼建设高度都要小于等于 \(m_i\)，考虑 \(i-1\) 这个位置，如果 \(m_{i-1} \ge m_i\)，则 \(i-1\) 这个位置建设高度也是 \(m_i\)，接下来的位置同理……
但如果 \(m_{i-1} < m_i\)，则 \(i-1\) 位置的建楼高度就是 \(m_{i-1}\)，从这里我们可以得到一个结论：如果 \(j\) 是 \(i\) 左边第一个使得 \(m_j < m_i\) 的位置，则当位置 \(i\) 作为所有楼中的最高楼时，从 \(j+1\) 到 \(i\) 这一段的建楼高度都是 \(m_i\)。
仿照前缀和的思想，我们可以定义 \(lsum_i\) 表示当位置 \(i\) 作为最高楼时，从 \(1 \sim i\) 的建楼总高度，则有 \(lsum_i = lsum_j + (i - j) \times m_i\)，其中 \(j\) 表示 \(m_i\) 左边第一个有 \(m_j < m_i\) 的位置，而每一个 \(i\) 对应的这个 \(j\) 可以通过单调栈在 \(O(n)\) 的时间复杂度下全部求出。同理，还可以定义 \(rsum_i\) 表示当位置 \(i\) 作为最高楼时，从 \(i \sim n\) 的建楼总高度，则有 \(rsum_i = rsum_j + (j - i) \times m_i\)，\(j\) 表示 \(m_i\) 右边第一个有 \(m_j < m_i\) 的位置。
求出所有的 \(lsum_i\) 和 \(rsum_i\) 之后，如果位置 \(i\) 作为最高楼的位置，那么总的建楼高度为 \(lsum_i + rsum_i - m_i\)，因而只需扫描一遍找到最优的位置即可。
参考代码
#include <cstdio>
#include <stack>
#include <algorithm>
using std::stack;
using std::min;
using ll = long long;
const int N = 500005;
int m[N], ans[N];
int l[N], r[N]; // l[i]/r[i]表示左边/右边第一个小于m[i]的位置
ll lsum[N], rsum[N];
int main()
{
int n; scanf("%d", &n);
for (int i = 1; i <= n; i++) scanf("%d", &m[i]);
stack<int> s;
for (int i = 1; i <= n; i++) {
while (!s.empty() && m[i] < m[s.top()]) {
r[s.top()] = i; s.pop();
}
s.push(i);
}
while (!s.empty()) {
r[s.top()] = n + 1; s.pop();
}
for (int i = n; i >= 1; i--) {
while (!s.empty() && m[i] < m[s.top()]) {
l[s.top()] = i; s.pop();
}
s.push(i);
}
while (!s.empty()) {
l[s.top()] = 0; s.pop();
}
for (int i = 1; i <= n; i++) {
lsum[i] = lsum[l[i]] + 1ll * (i - l[i]) * m[i];
}
for (int i = n; i >= 1; i--) {
rsum[i] = rsum[r[i]] + 1ll * (r[i] - i) * m[i];
}
int mid = 0; ll maxsum = 0;
for (int i = 1; i <= n; i++) {
ll sum = lsum[i] + rsum[i] - m[i];
if (sum > maxsum) {
maxsum = sum; mid = i;
}
}
ans[mid] = m[mid];
for (int i = mid - 1; i >= 1; i--) {
ans[i] = min(ans[i + 1], m[i]);
}
for (int i = mid + 1; i <= n; i++) {
ans[i] = min(ans[i - 1], m[i]);
}
for (int i = 1; i <= n; i++) printf("%d ", ans[i]);
return 0;
}
习题：P2422 良好的感觉
解题思路
由于所有的元素都是正的，因此对于一个元素 \(a_i\) 来说，如果它作为某个区间中最不舒服的那一天，也就是该区间中最小的元素，这个区间越长越好（因为区间总和不可能因为区间变长而减小）。因此如果对于每一个 \(a_i\) 求出它左边、右边第一个小于 \(a_i\) 的位置 \(l_i, r_i\)，则以 \(a_i\) 作为区间最小值的最长区间就是 \([l_i + 1, r_i - 1]\)，那么对应的舒适程度为 \((r_i - l_i - 1) \times (a_{l_i+1} + \cdots + a_{r_i - 1})\)，找出最大的结果即可。
\(l_i, r_i\) 可以利用单调栈预处理求出，区间和的计算可以预处理前缀和来快速求得，时间复杂度 \(O(n)\)。
参考代码
#include <cstdio>
#include <algorithm>
#include <stack>
using std::max;
using std::stack;
using ll = long long;
const int N = 100005;
int a[N], l[N], r[N];
ll sum[N];
int main()
{
int n; scanf("%d", &n);
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]); sum[i] = sum[i - 1] + a[i];
}
stack<int> s;
for (int i = 1; i <= n; i++) {
while (!s.empty() && a[i] < a[s.top()]) {
r[s.top()] = i; s.pop();
}
s.push(i);
}
while (!s.empty()) {
r[s.top()] = n + 1; s.pop();
}
for (int i = n; i >= 1; i--) {
while (!s.empty() && a[i] < a[s.top()]) {
l[s.top()] = i; s.pop();
}
s.push(i);
}
while (!s.empty()) {
l[s.top()] = 0; s.pop();
}
ll ans = 0;
for (int i = 1; i <= n; i++) {
ans = max(ans, (sum[r[i] - 1] - sum[l[i]]) * a[i]);
}
printf("%lld\n", ans);
return 0;
}
习题：P6503 [COCI2010-2011#3] DIFERENCIJA
解题思路
考虑将 \(\sum \limits_{i=1}^{n} \sum \limits_{j=i}^{n} (\max \limits_{i\le k\le j} a_k-\min \limits_{i\le k\le j} a_k)\) 拆成 \((\sum \limits_{i=1}^{n} \sum \limits_{j=i}^{n} \max \limits_{i\le k\le j} a_k) - (\sum \limits_{i=1}^{n} \sum \limits_{j=i}^{n} \min \limits_{i\le k\le j} a_k)\)。
这里最大值那一项和最小值那一项可以分离开计算，并且两者计算方式类似，不妨先分析最大值那一项，最小值那一项同理。
考虑对每个 \(a_i\) 计算它对整个式子的贡献，\(a_i\) 要有贡献需要它作为一个区间的最大值，因此如果设 \(l_i\) 代表 \(a_i\) 左边第一个大于 \(a_i\) 的位置，\(r_i\) 代表 \(a_i\) 右边第一个大于 \(a_i\) 的位置，则此时有 \((i - l_i) \times (r_i - i)\) 个区间会以 \(a_i\) 作为区间最大值，因此这就是 \(a_i\) 对式子的贡献。
但是，如果一个区间内的最大值有好几个数相等，那么这种计算方式会重复计算。如何去重？
调整 \(l_i, r_i\) 的含义，让 \(l_i\) 和 \(r_i\) 中的其中一个改为左边/右边第一个大于等于 \(a_i\) 的位置，另一个不带等号，这样就不会导致重复计数。这样的 \(l_i\) 和 \(r_i\) 用单调栈预处理。
参考代码
#include <cstdio>
#include <stack>
using std::stack;
using ll = long long;
const int N = 300005;
int a[N], lmax[N], rmax[N], lmin[N], rmin[N];
int main()
{
int n; scanf("%d", &n);
for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
stack<int> smax, smin;
for (int i = 1; i <= n; i++) {
while (!smax.empty() && a[i] > a[smax.top()]) {
rmax[smax.top()] = i; smax.pop();
}
smax.push(i);
while (!smin.empty() && a[i] < a[smin.top()]) {
rmin[smin.top()] = i; smin.pop();
}
smin.push(i);
}
while (!smax.empty()) {
rmax[smax.top()] = n + 1; smax.pop();
}
while (!smin.empty()) {
rmin[smin.top()] = n + 1; smin.pop();
}
for (int i = n; i >= 1; i--) {
while (!smax.empty() && a[i] >= a[smax.top()]) {
lmax[smax.top()] = i; smax.pop();
}
smax.push(i);
while (!smin.empty() && a[i] <= a[smin.top()]) {
lmin[smin.top()] = i; smin.pop();
}
smin.push(i);
}
while (!smax.empty()) {
lmax[smax.top()] = 0; smax.pop();
}
while (!smin.empty()) {
lmin[smin.top()] = 0; smin.pop();
}
ll sum_max = 0, sum_min = 0;
for (int i = 1; i <= n; i++) {
sum_max += 1ll * (i - lmax[i]) * (rmax[i] - i) * a[i];
sum_min += 1ll * (i - lmin[i]) * (rmin[i] - i) * a[i];
}
printf("%lld\n", sum_max - sum_min);
return 0;
}
习题：P1823 [COI2007] Patrik 音乐会的等待
解题思路
由于两个人可以互相看到，为了避免重复计算，下面只考虑每个人的单个方向。
先假设每个人身高不一样，考虑一个人的右边，最远的互相看到的人就是右边第一个高于他的人，再右边的人就看不到了，因此可以维护一个单调递减的栈。当栈顶矮于当前正在处理的人时，进行出栈，并且出栈的人和当前这个人就是一对互相看到的人。注意如果出栈之后栈中仍有元素，则这也是一对互相看到的人，相当于此时的栈顶和当前这个人可以互相看到（相当于栈顶是当前这个人左边第一个比他高的人，两个人可以互相看到，但是栈里其他的人就不可能和当前的人互相看到了）。
参考代码
#include <cstdio>
#include <stack>
using std::stack;
using ll = long long;
const int N = 500005;
int h[N];
int main()
{
int n; scanf("%d", &n);
for (int i = 1; i <= n; i++) scanf("%d", &h[i]);
stack<int> s;
ll ans = 0;
for (int i = 1; i <= n; i++) {
while (!s.empty() && h[i] > s.top()) { // 这个地方不管是>还是>=都有正确性问题
ans++; s.pop();
}
if (!s.empty()) ans++;
s.push(h[i]);
}
printf("%lld\n", ans);
return 0;
}
这个程序不能通过样例，但却能获得 \(20\) 分，原因是当每个人的身高不会重复时程序是完全正确的。
而无法通过样例的原因是因为样例中存在重复身高的人，当单调栈的栈顶等于当前处理的人的身高时，不管此时出栈还是不出栈，都可能对后续的计算造成影响。例如，身高依次是 \([2,1,1,2]\)，实际上中间这两个身高为 \(1\) 的人和第一个人都可以形成互相看见的对，和最后一个人也都可以形成互相看见的对。而单调栈在相等时如果选择出栈，则第二个人与第四个人形成的互相看见的对没被统计到；如果选择不出栈，则第三个人和第一个人形成的互相看见的对没被统计到。
所以怎么样才能不遗漏计数呢？实际上栈中如果要维护连续的身高相等的人应该将他们视作一个整体，在栈中同时维护人的身高和人数，当要入栈的人身高和栈顶的人身高相等时，将人数打包。
参考代码
#include <cstdio>
#include <stack>
#include <utility>
using std::stack;
using std::pair;
using ll = long long;
using pii = pair<int, int>;
int main()
{
int n; scanf("%d", &n);
stack<pii> s; // 身高，人数
ll ans = 0;
for (int i = 1; i <= n; i++) {
int x; scanf("%d", &x);
int cnt = 1;
while (!s.empty() && x >= s.top().first) {
ans += s.top().second;
if (s.top().first == x) cnt += s.top().second;
s.pop();
}
if (!s.empty()) ans++;
s.push({x, cnt});
}
printf("%lld\n", ans);
return 0;
}
习题：P10798 「CZOI-R1」消除威胁
解题思路
首先分析“威胁”的两个条件和操作：
- 操作：\(A_i \to -A_i\)，这个操作只改变一个数的符号，不改变其绝对值。
- 条件 1：\(A_l = A_r\)，这个条件与数的符号有关，可以通过操作来影响。
- 条件 2：\(\max(|A_l|, |A_{l+1}|, \dots, |A_r|) = |A_l|\)，这个条件只与数的绝对值有关，因此无论如何改变符号，这个条件是否成立对于一个固定的区间 \([l,r]\) 来说是不变的。
目标是最小化威胁区间的数量，这意味着，对于任何一个满足条件 2 的潜在威胁区间 \([l,r]\)，都希望尽可能地不让它满足条件 1，即让 \(A_l \ne A_r\)。
符号的改变只在绝对值相同的数之间有意义，如果 \(|A_l| \ne |A_r|\)，那么 \(A_l\) 永远不可能等于 \(A_r\)。
因此，可以将问题聚焦于绝对值相同的数。对于所有绝对值为 \(V\) 的数，它们在序列中的位置为 \(p_1, p_2, \dots, p_k\)。
- 一个数对 \((p_a, p_b)\) 只有在满足条件 2（即它们之间没有绝对值大于 \(V\) 的数）时，才可能构成威胁。
- 如果 \((p_a, p_b)\) 和 \((p_b, p_c)\) 都是潜在威胁，那么 \(p_a, p_b, p_c\) 就应该被看作一个整体来分配符号，因为它们之间存在威胁的“传递性”。
- 这意味着可以将所有具有相同绝对值 \(V\) 且相互之间构成潜在威胁的索引们划分为若干个连续段。
如果一个连续段有 \(s\) 个索引：
- 如果其绝对值 \(V=0\)，无法改变符号，所有数都是 0。它们之间任意配对都构成威胁，总数为 \(s(s-1)/2\)。
- 如果 \(V \gt 0\)，可以分配正负号。为了最小化同号数对的数量，应将这 \(s\) 个数尽可能平均地分成两组（一组为 \(+V\)，一组为 \(-V\)）。设两组大小为 \(s_1\) 和 \(s_2\)，则最小威胁数为 \(s_1(s_1-1)/2 + s_2(s_2 - 1)/2\)。
问题的核心变为如何高效地找出这些连续威胁区间，可以使用单调栈，通过一次遍历在 \(O(N)\) 时间内解决问题。
维护一个存储索引的单调递减栈，从左到右遍历整个序列（将原始值全部转化为绝对值）。
- 出栈：不断比较当前元素和栈顶元素，如果栈顶元素更小，说明当前元素是栈顶元素右侧第一个比它大的元素。这意味着栈顶元素右边会被一个更高的值隔开，无法与后面的任何元素连通。因此，将栈顶元素弹出。
- 合并：经过上一步出栈后，如果栈不为空且栈顶与当前元素相等，说明两者之间没有绝对值更大的元素把它们隔开，它们可以构成威胁区间，同时更新对应的 \(s\)（该栈顶元素为起始的连续威胁区间个数）。此时，当前元素不入栈，因为它已经和栈顶元素“合并”。
- 入栈：如果栈为空，或者栈顶元素大于当前元素，则将当前元素入栈，这代表当前元素开始了一个新的潜在的威胁区间（成为一个单调序列的一部分）。
遍历结束后，那些 \(s \gt 0\) 的位置代表是连续威胁区间的起始位置，根据前文所述的计数方式计算最小威胁数，并累加到总答案中。
参考代码
#include <cstdio>
#include <stack>
using namespace std;
using ll = long long;
const int N = 5e5 + 5;
int a[N], cnt[N];
int main()
{
int n; scanf("%d", &n);
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]);
if (a[i] < 0) a[i] = -a[i];
}
stack<int> s; // 栈中存储索引，其对应的 a[] 值保持单调不增
for (int i = 1; i <= n; i++) {
// a. 出栈：将栈顶所有绝对值严格小于 a[i] 的元素弹出
// 因为 a[i] 的存在，使得这些被弹出的元素无法与 i 或 i 之后的元素构成潜在威胁
while (!s.empty() && a[s.top()] < a[i]) {
s.pop();
}
// b. 连接/合并：如果栈顶元素与当前元素绝对值相等
if (!s.empty() && a[s.top()] == a[i]) {
// 这说明 s.top() 和 i 之间没有绝对值更大的元素，它们可以构成威胁区间
// 将 i 与 s.top() 合并
cnt[s.top()]++;
// 注意：此时 i 不入栈，因为它已被合并
} else {
// c. 入栈：如果栈为空或栈顶元素更大，则 i 成为一个新的代表
s.push(i);
}
}
ll ans = 0;
for (int i = 1; i <= n; i++) {
if (cnt[i] > 0) {
// 大小 = 代表 i 本身(1) + 它连接到的其他元素数量(cnt[i])
int c = cnt[i] + 1;
if (a[i] == 0) {
// 值为 0，无法改变符号，任意配对都构成威胁
ans += 1ll * c * (c - 1) / 2;
} else {
// 值不为 0，可分配正负号，将 c 个数平分为两组来最小化威胁
int p1 = c / 2, p2 = c - p1;
ans += 1ll * p1 * (p1 - 1) / 2; // 正数内部的威胁
ans += 1ll * p2 * (p2 - 1) / 2; // 负数内部的威胁
}
}
}
printf("%lld\n", ans);
return 0;
}
浙公网安备 33010602011771号