二叉树与树

二叉树的概念与遍历

---

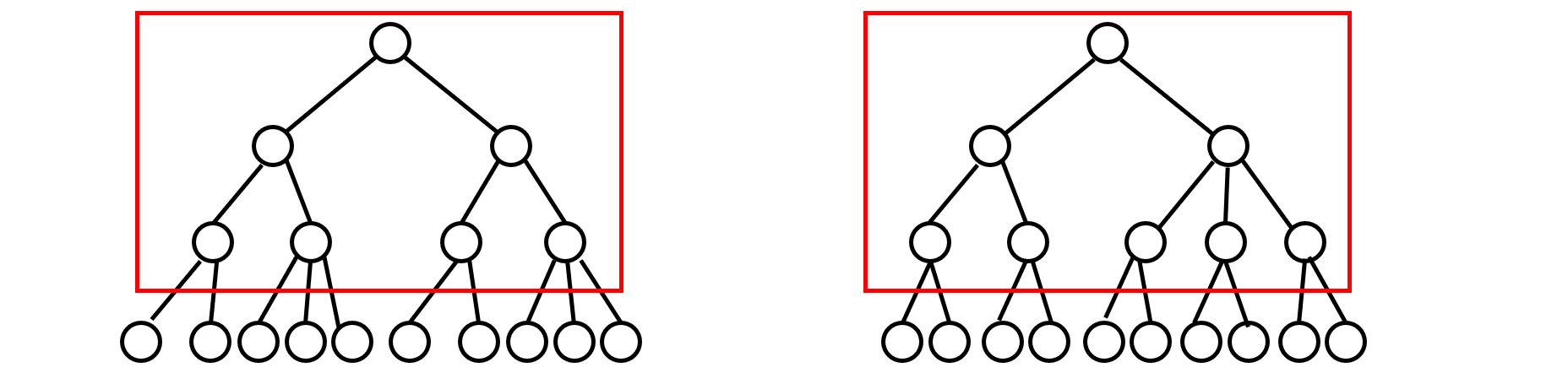
不定项选择题：2-3 树是一种特殊的树，它满足两个条件：

1. 每个内部节点有两个或三个子节点
2. 所有的叶节点到根的路径长度相同

如果一棵 2-3 树有 10 个叶节点，那么它可能有多少个非叶节点？

• A. 5
• B. 6
• C. 7
• D. 8

答案

CD。

---

P4913

#include <cstdio>
#include <algorithm>
using std::max;
const int N = 1e6 + 5;
int l[N],r[N];
int height(int u) { // 计算以u为根节点的子树的高度
	if (u==0) return 0;
	return 1+max(height(l[u]),height(r[u]));
}
int main()
{
	int n; scanf("%d",&n);
	for (int i=1;i<=n;i++) {
		int x,y; scanf("%d%d",&x,&y);
		l[i]=x;r[i]=y;
	}
	printf("%d\n", height(1));
    return 0;
}

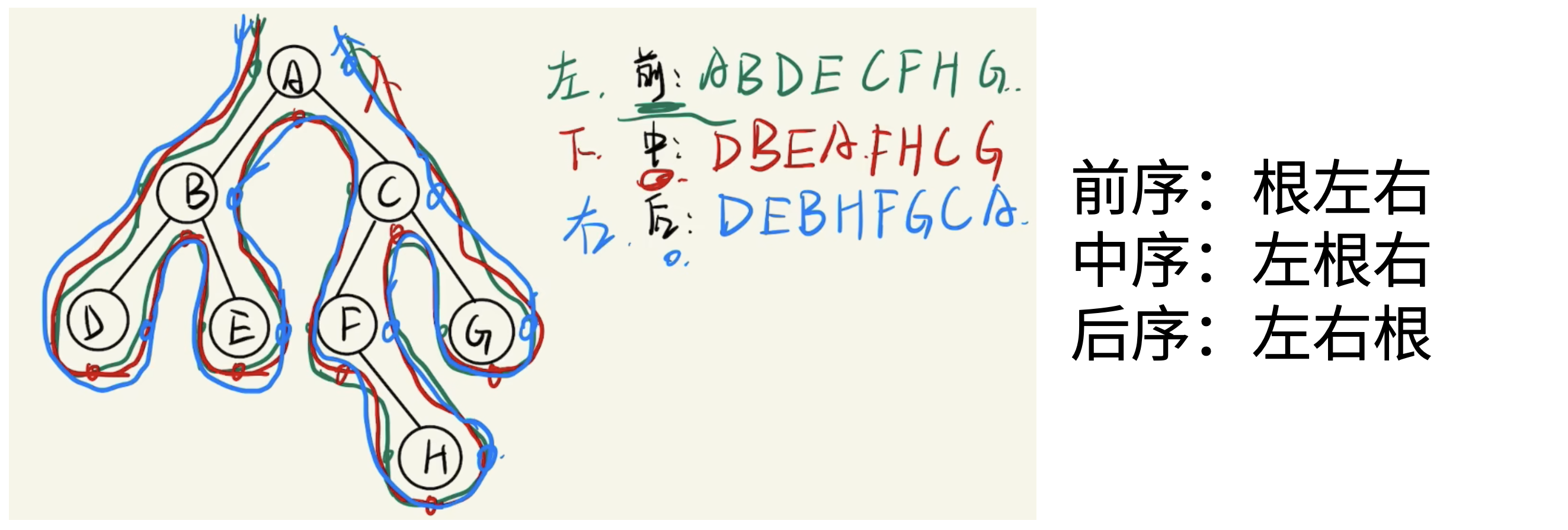
二叉树遍历的意思是将一棵二叉树从根结点开始，按照指定顺序，不重复、不遗漏地访问每一个结点。在完成一些任务中，必须要访问所有结点的信息，那么就需要按照某种方式不重复、不遗漏地访问所有结点。

答案

D

P1305

#include <cstdio>
const int N = 30;
char s[10];
int l[N],r[N];
void dfs(int u) {
	if (u==0) return;
	// 先序遍历：根左右
	char ch=u-1+'a';
	printf("%c", ch);
	dfs(l[u]); dfs(r[u]);
}
int main()
{
	int n; scanf("%d",&n);
	int root;
	for (int i=1;i<=n;i++) {
		scanf("%s", s);
		// s[0] s[1] s[2]
		int u=s[0]-'a'+1;
		int left=(s[1]=='*' ? 0 : s[1]-'a'+1);
		int right=(s[2]=='*' ? 0 : s[2]-'a'+1);
		l[u]=left; r[u]=right;
		if (i==1) root=u;
	}
	dfs(root);
    return 0;
}

已知一棵二叉树，可以确定它的三种遍历序列。反过来，已知两种遍历序列，能否确定二叉树？

根据先序和中序遍历序列确定一棵二叉树的步骤：

1. 根据先序序列第一个节点确定根节点
2. 根据根节点在中序序列中的位置，分割出左子树和右子树
3. 对左子树和右子树分别递归使用相同的方法继续分解

P1827

#include <cstdio>
#include <cstring>
const int N = 30;
char mid[N], pre[N]; // 中、前
void solve(int l1,int r1,int l2,int r2) {
	if (l1>r1 || l2>r2) return;
//	printf("mid[%d,%d], pre[%d,%d]\n", l1,r1,l2,r2);
	// mid[l1...r1]   pre[l2...r2]
	char root=pre[l2];
	// 在中序遍历中查找根节点的位置
	int pos;
	for (int i=l1;i<=r1;i++) {
		if (mid[i]==root) {
			pos=i; break;
		}
	}
	// pos就是中序的根节点位置
	// 左子树 mid[l1...pos-1] 右子树 mid[pos+1...r1]
	// 左子树大小 pos-l1
	// 右子树大小 r1-pos
	// pre[l2+1...l2+(pos-l1)]
	// pre[r2-(r1-pos)+1...r2]
	solve(l1,pos-1,l2+1,l2+(pos-l1));
	solve(pos+1,r1,r2-(r1-pos)+1,r2);
	printf("%c",root);
}
int main()
{
	scanf("%s%s",mid+1,pre+1);
	int len=strlen(mid+1);
	solve(1,len,1,len);
    return 0;
}

根据中序和后序遍历序列确定一棵二叉树的步骤：

1. 根据后序序列最后一个节点确定根节点
2. 根据根节点在中序序列中的位置，分割出左子树和右子树
3. 对左子树和右子树分别递归使用相同的方法继续分解

【练习】已知一棵二叉树的中序遍历序列为 CBEDAHGIJF，后序遍历序列为 CEDBHJIGFA，求出其先序遍历序列。

答案

ABCDEFGHIJ

---

选择题：前序遍历和中序遍历相同的二叉树为且仅为？

• A. 只有 1 个点的二叉树
• B. 根节点没有左子树的二叉树
• C. 非叶子节点只有左子树的二叉树
• D. 非叶子节点只有右子树的二叉树

答案

D。

前序遍历：根节点 → 左子树 → 右子树，中序遍历：左子树 → 根节点 → 右子树。

在前序遍历中，访问的第一个节点永远是当前树（或子树）的根节点。在中序遍历中，访问的第一个节点是当前树（或子树）的最左边的节点。

要使两个遍历序列相同，它们的第一个元素必须相同。这意味着，对于树中的任意一个节点（把它看作一个子树的根），它自身必须是该子树中最左边的节点。这种情况发生的唯一条件是：这个节点没有左子树。如果它有左子树，那么中序遍历就会先访问左子树，导致第一个被访问的节点不是根节点，从而与前序遍历产生差异。

这个“没有左子树”的条件必须对树中的每一个节点都成立。如果树的根节点没有左子树，那么遍历的下一个节点将是右子树的根。对于这个右子树，同样的逻辑也适用：它的根节点（即原始树根的右孩子）也不能有左孩子。这个规律依次传递下去，得出的结论是：整棵树从上到下，没有任何一个节点可以拥有左孩子。

---

【思考】已知先序和后序遍历序列，能否确定一棵二叉树？

答案

不能。例如先序遍历序列为 ABC，后序遍历序列为 CBA，可以画出 \(4\) 种不同的结构。

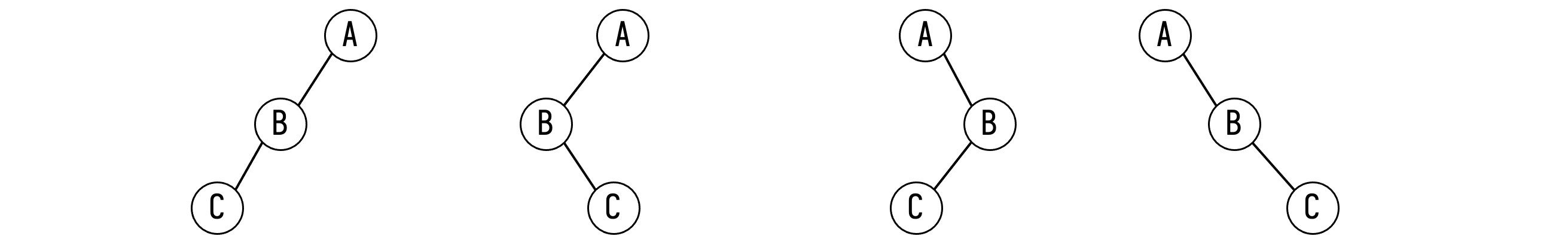
P1229

#include <iostream>
#include <string>
using std::string;
using std::cin;
using std::cout;
using ll = long long;
int main()
{
	string s1,s2;
	cin>>s1>>s2;
	ll ans=1;
	// 找会有多少个前序AB后序BA的
	int len=s1.size();
	for (int i=0;i<=len-2;i++) {
		// s1[i] s1[i+1]
		for (int j=0;j<=len-2;j++) {
			// 是否存在 s2[j]-s1[i+1]  s2[j+1]-s1[i]
			if (s2[j]==s1[i+1] && s2[j+1]==s1[i]) {
				ans*=2; break;
			}
		}
	}
	cout<<ans<<"\n";
    return 0;
}

例题：P4715 【深基16.例1】淘汰赛

#include <cstdio>
#include <algorithm>
using std::max;
using std::min;
const int N = 300;
int tree[N],winner[N], len;
void dfs(int u) {
	if (u>=len) return;
	dfs(u*2); dfs(u*2+1);
	if (tree[u*2]>tree[u*2+1]) {
		tree[u]=tree[u*2];
		winner[u]=winner[u*2];
	} else {
		tree[u]=tree[u*2+1];
		winner[u]=winner[u*2+1];
	}
}
int main()
{
	int n; scanf("%d",&n);
	len=1;
	for (int i=1;i<=n;i++) len*=2;
	for (int i=len;i<=2*len-1;i++) {
		scanf("%d",&tree[i]);
		winner[i]=i-len+1;
	}
	dfs(1);
	printf("%d\n", tree[2]<tree[3]?winner[2]:winner[3]);
    return 0;
}

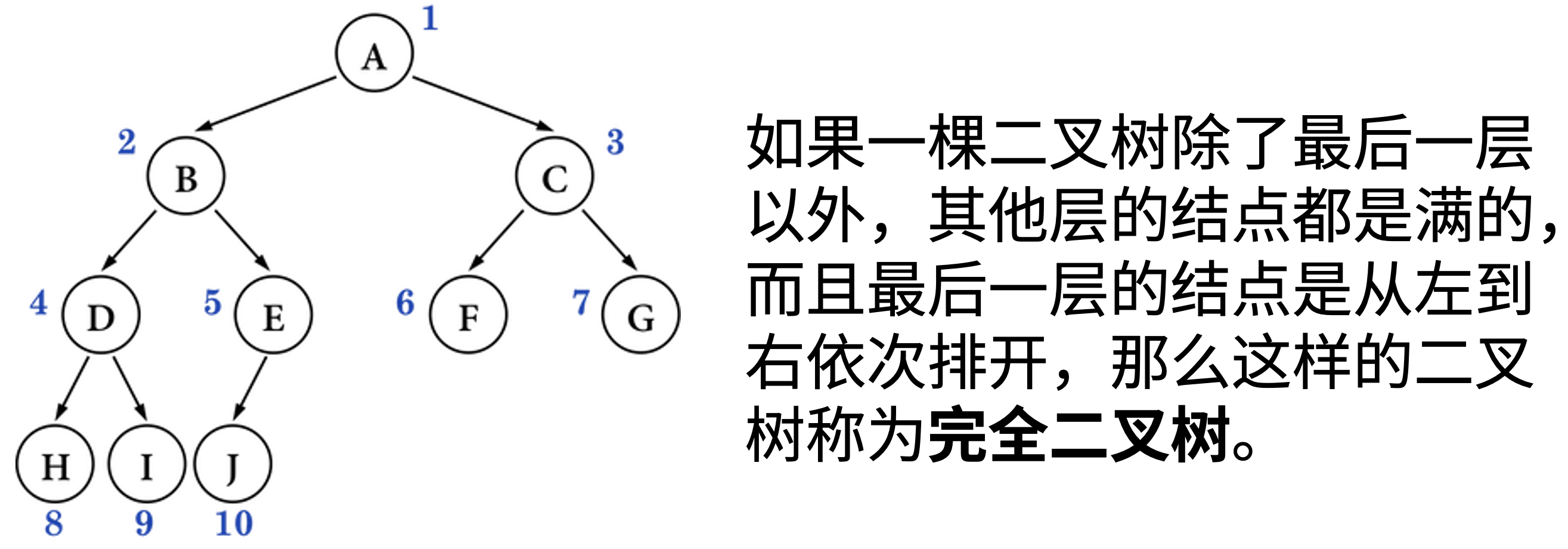
如果国家个数不是 \(2^n\) 个，而是一个任意正整数，这棵树的形态是？

---

答案

B。前 \(4\) 层都是满的，第 \(5\) 层至少有一个结点，因此至少有 \(1+2+4+8+1=16\) 个结点。

---

选择题：假设有一棵 \(h\) 层的完全二叉树，该树最多包含多少个节点？

• A. \(2^h-1\)
• B. \(2^{h+1}-1\)
• C. \(2^h\)
• D. \(2^{h+1}\)

答案

A。一个具有 \(h\) 层的完全二叉树，要使其节点数达到最多，那么它的所有层都必须被填满。当所有层都被填满时，这棵树就成了一棵完美二叉树。

一棵 \(h\) 层的完美二叉树的节点总数：

• 第 1 层有：\(2^0=1\) 个节点
• 第 2 层有：\(2^1=2\) 个节点
• 第 3 层有：\(2^2=4\) 个节点
• ……
• 第 \(h\) 层：\(2^{h-1}\) 个节点

总节点数就是将每一层的节点数相加，这是一个等比数列求和：\(总数 = 1+2+4+\cdots+2^{h-1}\)。

根据等比数列求和公式 \(S_n = \dfrac{a_1(1-q^n)}{1-q}\)，其中 \(a_1 = 1\)，\(q=2\)，\(n=h\)，\(总数 = \dfrac{1 \times (2^h-1)}{(2-1)} = 2^h-1\)。

因此，一棵 \(h\) 层的完全二叉树最多包含 \(2^h-1\) 个节点。

---

选择题：根节点深度为 \(0\)，一棵深度为 \(h\) 的满 \(k(k \gt 1)\) 叉树，即除最后一层无任何子节点外，每一层上的所有节点都有 \(k\) 个子节点的树，共有多少个节点？

• A. \(\dfrac{k^{h+1}-1}{k-1}\)
• B. \(k^{h-1}\)
• C. \(k^h\)
• D. \(\dfrac{k^{h-1}}{k-1}\)

答案

A。

总节点数 \(N = k^0 + k^1 + k^2 + \cdots + k^h\)，应用等比数列求和公式可以得到 \(\dfrac{k^{h+1}-1}{k-1}\)。

---

选择题：令根节点的高度为 1，则一棵含有 2021 个节点的二叉树的高度至少为？

• A. 10
• B. 11
• C. 12
• D. 2021

答案

B。

为了使含有 2021 个节点的二叉树高度最小，这棵树必须尽可能地“紧凑”和“平衡”。这种形态的树是完全二叉树。

一棵高度为 \(h\) 的完美二叉树（最紧凑的情况），其节点总数为 \(2^h-1\)。一棵高度为 \(h\) 的完全二叉树，其节点数 \(n\) 满足以下关系：它至少包含一个高度为 \(h-1\) 的完美二叉树和一个在第 \(h\) 层的节点，至多是一个高度为 \(h\) 的完美二叉树。因此，节点数 \(n\) 的范围是 \(2^{h-1} \le n \le 2^h-1\)。

需要找到满足 \(2^{h-1} \le 2021 \le 2^h-1\) 的最小整数 \(h\)。当 \(h=10\) 时，一个高度为 10 的完全二叉树，节点数范围为 \([2^9, 2^{10}-1]\)，即 \([512, 1023]\)。因为 \(2021 \lt 1023\)，所以高度为 10 的树不足以容纳 2021 个节点。当 \(h=11\) 时，一个高度为 11 的完全二叉树，节点数范围是 \([2^{10}, 2^{11}-1]\)，即 \([1024, 2047]\)。因为 \(1024 \le 2021 \le 2047\)，所以 2021 个节点可以构成一棵高度为 11 的完全二叉树。

---

选择题：一个深度为 5（根节点深度为 1）的完全 3 叉树，按前序遍历的顺序给节点从 1 开始编号，则第 100 号节点的父节点是第几号？

• A. 95
• B. 96
• C. 97
• D. 98

答案

正确答案是 C。

需要知道一个节点作为根时，它所包含的整个满子树一共有多少个节点。

一个深度为 \(d\) 的满 \(k\) 叉树的节点总数公式为 \((k^d - 1) / (k - 1)\)，本题中 \(k=3\)。

• 深度为 1 的子树（单个叶子节点）：\((3^1-1)/2=1\) 个节点。
• 深度为 2 的子树：\((3^2-1)/2=4\) 个节点。
• 深度为 3 的子树：\((3^3-1)/2=13\) 个节点。
• 深度为 4 的子树：\((3^4-1)/2=40\) 个节点。
• 深度为 5 的整棵树（如果是满的）：\((3^5-1)/2=121\) 个节点。

---

二叉树的综合应用

P1364

#include <cstdio>
#include <algorithm>
using std::min;
const int N = 105;
int n,ans,people;
int w[N],l[N],r[N],depth[N],s[N];
// depth记录每个节点的深度，s记录每个节点的子树人口总量
bool flag[N];
void dfs(int u, int d) {
	if (u==0) return;
	depth[u]=d;
	dfs(l[u],d+1); dfs(r[u],d+1);
	s[u]=w[u]+s[l[u]]+s[r[u]];
}
void solve(int u, int sum) { // 医院换到u时，距离和为sum
	if (u==0) return;
//	printf("sum=%d\n",sum);
	ans=min(ans,sum);
	// u->l[u]
	// 此时距离和的变化
	// l[u]的子树(s[l[u]])距离全都缩小了1
	// 其他人(总人口数-s[l[u]])距离增大1
	// 距离和 - s[l[u]] + (总人口数-s[l[u]])
	solve(l[u],sum-2*s[l[u]]+people); 
	solve(r[u],sum-2*s[r[u]]+people);
}
int main()
{
	scanf("%d",&n);
	for (int i=1;i<=n;i++) {
		flag[i]=true; // 先假设它是根节点
	}
	for (int i=1;i<=n;i++) {
		scanf("%d%d%d",&w[i],&l[i],&r[i]);
		people+=w[i];
		flag[l[i]]=false;
		flag[r[i]]=false; // 被作为孩子就不可能是根节点
	}
	int root;
	for (int i=1;i<=n;i++) {
		if (flag[i]) {
			root=i; break;
		}
	}
//	printf("root=%d\n",root);
	dfs(root,0);
	ans=0;
	// 先计算假如以root作为医院位置，距离和是多少
	for (int i=1;i<=n;i++) ans+=w[i]*depth[i];
	// 接下来要考虑换其他位置作为医院，距离和的变化
	solve(root,ans);
	printf("%d\n",ans);
    return 0;
}

从二叉树到多叉树

多叉树和二叉树最大的不同在于，它的每个节点可以有任意数量的子节点。标准库中的 std::vector 是一个动态数组，可以根据需要增长，这使得它成为存储数量不定的子节点的理想工具。

最常用和最高效的方法是邻接表示法。

1. 给节点编号：首先，给树上的每个节点一个唯一的整数 ID，例如从 \(0\) 到 \(n-1\) 或者 \(1\) 到 \(n\)。
2. 建立邻接表：创建一个 vector 的 vector，即 vector<vector<int>> tree。
3. 存储关系：tree[i] 本身是一个 vector，里面存储了所有以节点 \(i\) 为父节点的子节点的 ID。

例如，tree[u] = {v1, v2, v3} 就表示节点 u 有三个子节点，分别是 v1，v2 和 v3。

这种方法的优点是：

• 空间高效：只存储存在的边（父子关系），总空间复杂度为 \(O(n)\)，其中 \(n\) 是节点数。
• 实现简单：很容易添加一条边（即一个父子关系）。
• 遍历方便：很容易找到一个节点的所有子节点，只需遍历对应的 vector 即可。

假设有这样一棵树，节点 1 的子节点是 2, 3, 4，节点 2 的子节点是 5，节点 4 的子节点是 6 和 7。结构如下：

   1
 / | \
2  3  4
|    / \
5   6   7

#include <iostream>
#include <vector>
using namespace std;

// 使用邻接表示法存储树
// tree[u] 是一个 vector，存储了节点 u 的所有子节点
vector<vector<int>> tree;

// 深度优先搜索 (DFS) 遍历树
// u: 当前遍历到的节点
// depth: 当前节点的深度（用于格式化输出）
void dfs(int u, int depth) {
	// 打印当前节点，并根据深度进行缩进
	for (int i = 0; i < depth; i++) {
		cout << " ";
	}
	cout << "node " << u << "\n";
	// 递归地访问所有子节点
	for (int child : tree[u]) {
		dfs(child, depth + 1);
	}
}
int main()
{
	// 假设有 7 个节点，编号从 1 到 7
	int n = 7;
	// 需要 n+1 的大小，因为节点编号从 1 开始
	tree.resize(n + 1);
	// 构建树的结构
	// 添加边来表示父子关系
	// tree[parent].push_back(child);
	// 节点 1 的子节点是 2, 3, 4
	tree[1].push_back(2);
	tree[1].push_back(3);
	tree[1].push_back(4);
	// 节点 2 的子节点是 5
	tree[2].push_back(5);
	// 节点 4 的子节点是 6, 7
	tree[4].push_back(6);
	tree[4].push_back(7);
	// 假设节点 1 是根节点
	int root = 1;
	cout << "Start from the root node " << root << " and perform DFS traveral\n";
	// 从根节点开始遍历
	dfs(root, 0);
	return 0;
}

代码讲解

1. vector<vector<int>> tree;：这是核心数据结构，tree 是一个 vector，它的每个元素是另一个 vector<int>。tree[i] 就代表了节点 i 的子节点列表。
2. tree.resize(n + 1);：调整 tree 的大小以容纳所有节点，因为节点的编号从 1 开始，所以需要 n+1 的空间（索引 0 将被闲置）。
3. tree[parent].push_back(child);：这是添加父子关系的关键，例如 tree[1].push_back(2); 表示“节点 2 是节点 1 的一个子节点”。
4. dfs(int u, int depth)：这是一个标准的深度优先搜索函数，用于演示如何使用建立起来的树结构。
   • 它首先处理当前节点 u。
   • 然后，它通过 for (int child : tree[u]) 循环遍历 u 的所有子节点。
   • 对每个子节点，它递归调用 dfs，从而深入到树的下一层。

---

当遇到以下情况时，通常需要在建树时建立双向边：题目只给出 \(n-1\) 条边，每条边用 \(u\) 和 \(v\) 表示两者之间有一条边。此时，由于在输入时无法确定谁是树上深度更深/浅的那个，必须建立双向边。如果只建单向边 \(u \rightarrow v\)，万一实际遍历过程中 \(v\) 离根节点更近，由于没有构建 \(v \rightarrow u\) 这条边，使得遍历过程不正确。

处理方式

// 读入 u, v
tree[u].push_back(v);
tree[v].push_back(u); // 关键：建立反向边

遍历时的注意事项：因为建立了双向边，在进行深度优先搜索（DFS）或广度优先搜索（BFS）时，当从节点 \(p\) 走到节点 \(u\)，必须防止立即从 \(u\) 又走回 \(p\)。所以，遍历函数通常需要多一个参数来记录父节点。

void dfs(int u, int parent) {
	// ... 对 u 进行操作 ...

	for (int v : tree[u]) {
		if (v == parent) { // 如果邻居是来的地方，就跳过
			continue;
		}
		dfs(v, u); // 递归下去，此时 u 是 v 的父节点
	}
}

// 调用时，根节点的父节点可以设为一个不存在的节点，如 0 或 -1
// dfs(root, 0);

---

习题：P5908 猫猫和企鹅

参考代码

#include <cstdio>
#include <vector>
using namespace std;
const int N = 100005;
// 使用邻接表来存储树的结构
// tree[i] 是一个动态数组，存储所有与节点i直接相连的节点
vector<vector<int>> tree;
// n: 居住区数量, d: 猫猫愿意走的最大距离, ans: 最终答案（可以拜访的企鹅数量）
int n, d, ans;
/**
 * @brief 深度优先搜索函数
 * 
 * @param cur 当前正在访问的节点
 * @param fa  当前节点的父节点（防止向回走）
 * @param dis 当前节点到根节点1的距离 
 */
void dfs(int cur, int fa, int dis) {
    // 如果当前节点的距离已经达到了d
    // 那么它的所有子节点的距离都将大于d，无需继续向下探索
	if (dis == d) return;
    // 遍历当前节点的所有邻居
	for (int to : tree[cur]) {
        // 如果邻居节点就是父节点，则跳过，避免走回头路
		if (to == fa) continue;
        // 如果邻居节点不是父节点，说明它是一个可以访问的子节点
        // 猫猫可以拜访住在这个子节点的小企鹅，所以答案加一
		ans++;
        // 递归地访问这个子节点
        // 子节点地父节点是当前节点(cur)，距离是当前距离加一(dis + 1)
		dfs(to, cur, dis + 1);
	}
}
int main()
{
    // 读取节点数n和最大距离d
	scanf("%d%d", &n, &d);
    tree.resize(n + 1);
    // 循环n-1次，读取所有的道路信息，构建邻接表
	for (int i = 1; i < n; i++) {
		int u, v; scanf("%d%d", &u, &v);
        // 因为道路输入时不知道哪个节点深度大，所以要在两个节点的邻接表中都添加对方
		tree[u].push_back(v);
		tree[v].push_back(u);
	}
    // 从根节点1开始进行深度优先搜索
    // 初始状态：当前节点为1，父节点为0（一个不存在的节点），到根的距离为0
	dfs(1, 0, 0);
    // 输出最终统计的数量
	printf("%d\n", ans);
	return 0;
}

---

假设有 5 个节点，边是：(1, 2)，(1, 3)，(2, 4)，(2, 5)。这棵树可以画成很多样子，但它们的结构本质上是一样的。

      1          2          4
     / \        /|\         |
    2   3      4 1 5        2
   / \           |         / \
  4   5          3        1   5
                          |
                          3
// 以上三种画法描述的是同一个结构

如果一棵树不指定根节点，那么所有节点在结构上都是平等的，没有哪个节点天生就是“根”。边 \((u,v)\) 只表示 \(u\) 和 \(v\) 是相邻的，没有 \(u\) 是 \(v\) 的父亲或孩子这种说法，这样的树称为无根树。

既然无根树里所有节点都“平等”，那么该如何下手呢？处理无根树的方法往往是：任选一个点作为根节点，将其“变成”一棵有根树。

这个过程就像把一张平铺的地图上的某个城市“拎起来”，其他城市因为重力自然下垂，形成了层次分明的结构。

---

当树的边带有属性（例如权重、长度、颜色、费用等）时，之前用的 vector<vector<int>> 就不够了，因为它只能存储“连接到哪个节点”，无法存储“这条连接的属性是什么”。

可以使用结构体扩展数据结构。

1. 定义一个 Edge 结构体，用来封装一条边的所有信息：它指向哪个节点（to），以及它的各种属性（如 weight）。
2. 邻接表从 vector<vector<int>> 升级为 vector<vector<Edge>>。
3. tree[u] 现在是一个存储 Edge 对象的 vector，其中每个 Edge 对象都描述了从 u 出发的一条边。

假设要解决一个问题：在一棵带权树上，求根节点到所有其他节点的距离。

#include <iostream>
#include <vector>
using namespace std;
using ll = long long;
// 1. 定义 Edge 结构体
struct Edge {
    int to;     // 这条边指向的节点
    int weight; // 这条边的权重
};
int n;
// 2. 邻接表存储 Edge 结构体
vector<vector<Edge>> tree;
// 用于存储根节点到各点距离的数组
vector<ll> dist;
// DFS 遍历带权树
// u：当前节点
// p：父节点（用于防止走回头路）
// current_dist：从根节点到 u 的距离
void dfs(int u, int p, ll current_dist) {
    dist[u] = current_dist;
    // 3. 遍历邻接表时，取出的元素是 Edge 对象
    for (const Edge& edge : tree[u]) {
        int v = edge.to;
        int w = edge.weight;
        if (v == p) {
            continue;
        }
        // 递归到子节点，并累加上这条边的权重
        dfs(v, u, current_dist + w);
    }
}
int main()
{
    cout << "Please input the number of nodes:";
    cin >> n;
    tree.resize(n + 1);
    dist.resize(n + 1);
    cout << "\nPlease input " << n - 1 << " edges (u v weight)\n";
    for (int i = 0; i < n - 1; i++) {
        int u, v, w;
        cin >> u >> v >> w;
        // 建立双向带权边
        tree[u].push_back({v, w});
        tree[v].push_back({u, w});
    }
    int root = 1; // 假设 1 是根节点
    dfs(root, 0, 0);
    cout << "From the root node " << root << " to other nodes\n";
    for (int i = 1; i <= n; i++) {
        cout << "The distance to node " << i << " is " << dist[i] << "\n";
    }
    return 0;
}

---

习题：P6111 [USACO18JAN] MooTube S

解题思路

题目要求找到所有与视频 \(v\) 的“相关性”至少为 \(k\) 的其他视频。两个视频的相关性是它们之间路径上所有边相关性的最小值。因此，这等价于从 \(v\) 到其他点的路径上，每一条边的相关性都必须大于等于 \(k\)。

对于一个查询 \((k, v)\)，可以想象只保留原树中那些相关性大于等于 \(k\) 的边能走，而暂时忽略所有小于 \(k\) 的边。以 \(v\) 为根节点遍历整棵树时，当某条边相关性不足 \(k\) 时，这条边就相当于无法通行，在这个条件下统计一共经过多少个其他节点即可。

参考代码

#include <cstdio>
#include <vector>
using namespace std;
// 边的结构体，包含目标节点和相关性值
struct Edge {
    int to, r; // to：边的另一个端点，r：相关性
};
// 使用邻接表存储树的结构
vector<vector<Edge>> tree;
/**
 * @brief 深度优先搜索
 * 
 * @param u    当前正在访问的视频节点
 * @param p    当前节点的父节点（用于防止DFS走回头路）
 * @param k    本次查询的相关性阈值k
 * @return int 从节点u出发，在只能走相关性>=k的边的情况下， 能访问到的节点总数（包括u自身）
 */
int dfs(int u, int p, int k) {
    // 初始化结果为1，代表计数当前节点u
    int res = 1;
    // 遍历与当前节点u相连的所有边
    for (const Edge& edge : tree[u]) {
        int v = edge.to;
        int r = edge.r; // 这条边的相关性
        // 过滤条件：
        // 1. v == p 不走回头路
        // 2. r < k 不走相关性小于阈值k的边
        if (v == p || r < k) continue;
        // 如果可以通过这条边，则递归地访问子节点v
        // 并将子树返回的节点数累加到结果中
        res += dfs(v, u, k);
    }
    // 返回符合条件的数量
    return res;
}
// 处理单次查询的函数
void solve() {
    int k, v; scanf("%d%d", &k, &v); 
    // 减1是因为求的是“其他”相关视频的数量
    printf("%d\n", dfs(v, 0, k) - 1);
}
int main()
{
    int n, q;
    scanf("%d%d", &n, &q); // 读取视频数和查询数
    tree.resize(n + 1); // 调整邻接表大小
    for (int i = 1; i < n; i++) {
        int x, y, z;
        scanf("%d%d%d", &x, &y, &z);
        // 由于是无根树，需要在两个节点的邻接表中都添加这条边
        tree[x].push_back({y, z});
        tree[y].push_back({x, z});
    }
    // 循环处理q次查询
    for (int i = 1; i <= q; i++) {
        solve();
    }
    return 0;
}

---

P2420

#include <cstdio>
#include <vector>
#include <cmath>
using std::vector;
using std::abs;
using ll = long long;
const int N = 1e5+5;
struct Edge {
	int v,w;
};
vector<Edge> tree[N]; // tree[i]存储i连出去的边
int n,s[N]; // s[i] 从根节点(假设为1)到i的一路上的边权异或起来
void dfs(int u, int from) {
	// 当前节点是u，来源是from
	// range-for
	for (Edge e : tree[u]) {
		if (e.v!=from) {
			// u->e.v
			// 1到v的异或等于1到u的异或再异或上这条边
			s[e.v]=s[u]^e.w; 
			dfs(e.v,u);
		}
	}
}
int main()
{
	scanf("%d",&n);
	for (int i=1;i<=n-1;i++) {
		int u,v,w;
		scanf("%d%d%d",&u,&v,&w);
		// 建树时取双向边
		tree[u].push_back({v,w});
		tree[v].push_back({u,w});
	}
	// 整棵树以谁为根无所谓（无根树）
	// 假设强制以1为根
	dfs(1,0); 
	int m; scanf("%d",&m);
	for (int i=1;i<=m;i++) {
		int u,v; scanf("%d%d",&u,&v);
		printf("%d\n",s[u]^s[v]);
	}
    return 0;
}