模拟
竞赛中有一类问题,被称为“模拟题”,设计程序完整地按照题目叙述的方式运行得到答案,这一类问题通常对思维与算法设计的要求不高,但要求扎实的编程基本功。
例题:P2670 [NOIP2015 普及组] 扫雷游戏
给出一个 \(n \times m\) 的网格,有些格子埋有地雷。求问这个棋盘上每个没有地雷的格子周围(上、下、左、右和斜对角)的地雷数。
输入第一行的两个整数 \(n\) 和 \(m\),表示网格的行数和列数,接下来的 \(n\) 行,每行 \(m\) 个字符,描述了雷区中的地雷分布情况。字符 * 表示相应格子是地雷格,字符 ? 表示相应格子是非地雷格。\(m\) 和 \(n\) 不超过 \(100\)。
输出包含 \(n\) 行,每行 \(m\) 个字符,描述整个雷区。用 * 表示地雷格,用周围的地雷个数表示非地雷格。
分析:根据题意,对于每个非地雷格的格子,只需要统计其八个边上方向的格子中的地雷数量。如果需要统计的格子的坐标是 \((x,y)\),那么它左上角的坐标是 \((x-1,y-1)\)。
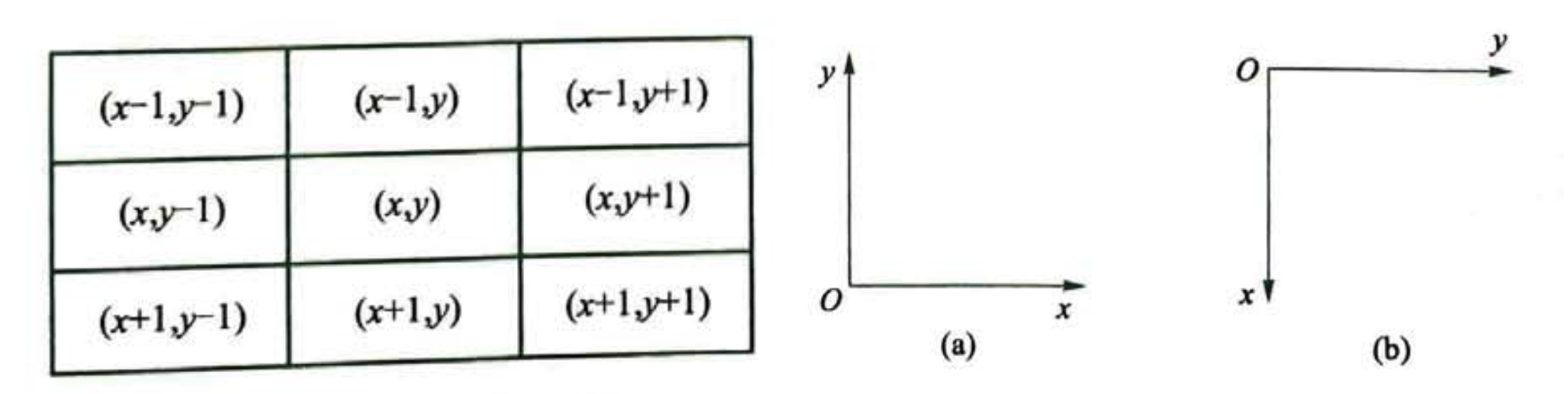
一般情况下,竞赛程序中涉及的坐标系表示方法(b)相对于日常接触的直角坐标系(a)略有不同,比如在二维数组里,一般原点对应的是左上角,这样就能很方便地将行数和 \(x\) 对应起来,列数与 \(y\) 对应起来,比如第一行第二列可以表示成 \((1,2)\),便于存储和查询。
没有必要列举出 8 个 if 语句逐一判定这个格子的 8 个方向是否有雷,只要预先定义好的这 8 个方向的格子相对于这个格子的偏移量,然后对这个偏移量数组循环即可。
还有一点需要注意的是边界问题。在枚举某些边界上的格子时,它的某些方向会超出这个二维阵列,如果不经过特殊处理很容易造成数组越界。有两种方法可以解决这个问题,一是对需要查询的坐标进行范围判断;二是可以在这个二维阵列外围加一圈“空白的虚拟非雷区”参与统计。
#include <cstdio>
const int N = 105;
char mine[N][N]; // 全局变量区定义的变量默认初始化为0,注意这个0是指'\0',而不是字符'0'
int ans[N][N];
// 某点的8个方向相邻位置的偏移量
int dx[8] = {-1, -1, -1, 0, 0, 1, 1, 1};
int dy[8] = {-1, 0, 1, -1, 1, -1, 0, 1};
int main()
{
int n, m; scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) {
scanf("%s", mine[i] + 1);
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
for (int k = 0; k < 8; k++) {
int x = i + dx[k], y = j + dy[k];
// 因为地雷数组占用的范围是[1~n][1~m],相当于外面有一圈“虚拟边框”
if (mine[x][y] == '*') ans[i][j]++;
}
}
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (mine[i][j] == '*') printf("*");
else printf("%d", ans[i][j]);
}
printf("\n");
}
return 0;
}
例题:P1042 [NOIP2003 普及组] 乒乓球
华华和朋友打乒乓球,得到了每一球的输赢记录:W 表示华华得一分,L 表示对手得一分,E 表示比赛信息结束。一局比赛刚开始时比分为 0:0。每一局中达到 11 分或者 21 分(赛制不同),且领先对方 2 分或以上的选手可以赢得这一局。现在要求输出在 11 分制和 21 分制两种情况下的每一局得分。输入数据每行至多有 25 个字母,最多有 2500行。
分析:根据题意,只需要对读入的内容进行统计即可。使用数组 rec 记录下从开始到结束的得分情况,如果是华华赢了就记为 1,反之记为 0,读到 E 的时候就直接退出读入过程,读到换行符时要忽略,同时记录他们一共打了多少球 len。
然后分别对两种赛制进行计算。首先记分板上双方(c1 和 c2)都是 0,如果华华赢了,c1 就增加 1,否则 c2 就增加 1,如果发现记分板上得分高的一方达到了赛制要求的球数,而且分差也足够,就将记分板的得分输出,同时记分板清零开始下一局。到最后还要输出正在进行中的比赛的得分。
#include <cstdio>
#include <cmath>
#include <algorithm>
using std::max;
using std::abs;
const int N = 1e5 + 5;
int rec[N];
int win[2] = {11, 21}; // 两种赛制的获胜得分
int main()
{
int len = 0;
while (true) {
char ch; scanf("%c", &ch); // 不断读入比赛记录
if (ch == 'E') break;
// 注意ch可能会读到换行符,所以必须只记录W和L
if (ch == 'W') rec[++len] = 1; // 华华赢
else if (ch == 'L') rec[++len] = 0; // 华华输
}
for (int i = 0; i < 2; i++) { // 两种赛制循环
int c1 = 0, c2 = 0;
for (int j = 1; j <= len; j++) {
if (rec[j] == 1) c1++;
else c2++;
// 获胜者达到对应分数并且超出对手两分
if (max(c1, c2) >= win[i] && abs(c1 - c2) >= 2) {
printf("%d:%d\n", c1, c2);
c1 = c2 = 0;
}
}
printf("%d:%d\n", c1, c2); // 还要输出最终的即时比分
if (i == 0) printf("\n");
}
return 0;
}
本题思路很简单,直接根据题意和生活常识模拟即可,但还是有一些需要注意的地方:
- 记录比赛记录的数组要开够,看清楚题目描述中所说的最多输入行数以及每行最多的字母数量。
- 读到 E 就可以停止读入了,后面的都忽略掉,同时遇到换行符之类的与比赛结果无关的字符也要忽略。
- 注意要分差 2 分及以上才能结算一局比赛的结果。
- 最后还要输出最后一局正在进行中比赛比分,就算是刚刚完成一局也要输出 0:0,以及第一种赛制和第二种赛制间有一个空行。
题目中的描述可能包含关键信息,所以一定要认真审题。
例题:P1563 [NOIP2016 提高组] 玩具谜题
\(n \ (n<100000)\) 个玩具小人依次逆时针围成一个圈,有些小人面向圈内,有些面向圈外。一开始第一个小人手里有眼镜。从这只小人开始进行 \(m \ (m<100000)\) 次传递。拿着眼镜的小人将眼镜传递给左手 / 右手边的第 \(s \ (s<n)\) 个人。已知每个玩具小人的职业(长度不超过 \(10\) 的字符串)和朝向(\(0\) 表示朝圈内,\(1\) 表示超圈外),以及每次传递的方向(\(0\) 表示往这只小人的左边,\(1\) 表示往右边)和传过的玩具人数,求最后眼镜在谁手上,输出职业。
分析:如果模拟现实中击鼓传花的过程,一个传一个,模拟眼镜在谁的手上,考虑到数据范围很大,两重循环的做法会超时。
把手里拥有眼镜的第一个玩具小人称为 \(0\) 号小人(这里从 \(0\) 开始比较方便,最后一个小人是 \(n-1\) 号)。当他面朝内时,往右边传递 \(3\) 只小人,就会变成 \(0+3=3\) 号小人拥有礼物。如果 \(0\) 号小人往左边传递 \(3\) 只小人,就会变成 \(0-3=-3\) 号小人拿着眼镜,显然没有 \(-3\) 号小人。假设总共有 \(7\) 只小人,考虑 \(0\) 号小人和 \(7\) 号小人等价(因为 \(6\) 号小人的下一个就是 \(0\) 号小人),\(1\) 号小人和 \(8\) 号小人等价,……,可以推出:\(-3\) 号小人和 \(-3+7=4\) 号小人等价。面朝内的小人往右边数 \(s\) 个就是编号增加 \(s\),往左边数就是编号减少 \(s\)。如果得到的编号不在 \(0 \sim n-1\) 的范围内,则需要通过增减 \(n\) 调整到这个范围内。为了达到这个目的,可以使用取余数的方式。
如果小人面朝外,那么方向和加减的关系就和上面一种情况反过来,但是依然需要调整到 \(0 \sim n-1\) 的范围内。
#include <cstdio>
const int N = 1e5 + 5;
const int LEN = 15;
struct Toy { // 使用结构体存储玩具的朝向和职业
int face;
char job[LEN];
};
Toy t[N];
int main()
{
int n, m; scanf("%d%d", &n, &m);
for (int i = 0; i < n; i++) {
scanf("%d%s", &t[i].face, t[i].job);
}
int now = 0;
for (int i = 1; i <= m; i++) {
int a, s; scanf("%d%d", &a, &s);
if (t[now].face == 0 && a == 1) { // 朝向内,向右,编号+s
now = (now + s) % n;
} else if (t[now].face == 0 && a == 0) { // 朝向内,向左,编号-s
now = (now + n - s) % n;
} else if (t[now].face == 1 && a == 1) { // 朝向外,向右,编号-s
now = (now + n - s) % n;
} else if (t[now].face == 1 && a == 0) { // 朝向外,向左,编号+s
now = (now + s) % n;
}
}
printf("%s\n", t[now].job);
return 0;
}
这段代码还能进行一些精简,利用异或运算将四种情况合并,参考代码如下:
参考代码
#include <cstdio>
const int N = 1e5 + 5;
const int LEN = 15;
struct Toy { // 使用结构体存储玩具的朝向和职业
int face;
char job[LEN];
};
Toy t[N];
int main()
{
int n, m; scanf("%d%d", &n, &m);
for (int i = 0; i < n; i++) {
scanf("%d%s", &t[i].face, t[i].job);
}
int now = 0;
for (int i = 1; i <= m; i++) {
int a, s; scanf("%d%d", &a, &s);
int flag = (t[now].face ^ a) * 2 - 1;
now = (now + n + flag * s) % n;
}
printf("%s\n", t[now].job);
return 0;
}
习题:P4924 [1007] 魔法少女小Scarlet
首先把 \(1\) 到 \(n^2\) 的正整数按照从左往右,从上至下的顺序填入 \(n \times n \ (n \le 500)\) 的二维数组中,并进行 \(m \ (m \le 500)\) 次操作,使二维数组上一个奇数阶方阵按照顺时针或者逆时针旋转 \(90°\)。每次操作给出 \(4\) 个整数 \(x,y,r,z\),表示把以第 \(x\) 行第 \(y\) 列为中心的 \(2r+1\) 阶矩阵按照某种时针方向旋转,其中 \(z=0\) 表示顺时针,\(z=1\) 表示逆时针。要求输出最终所得的矩阵。
解题思路
直接在原数组上进行旋转操作非常困难,因为元素的移动会覆盖掉尚未处理的旧数据,最佳策略是引入一个与主矩阵大小相同的临时辅助矩阵。
旋转分为两步
- 计算并暂存:遍历要旋转的子区域,对于目标区域的每一个位置 \((i,j)\),根据旋转公式计算出它应该接收来自原矩阵中哪个位置的元素,并将这个元素值存入临时矩阵的 \((i,j)\) 位置。
- 写回:当旋转后的子区域在临时矩阵中完整生成后,再将临时矩阵中这个区域的数据原封不动地复制回主矩阵的对应位置。
对于一个边长为 \(len\) 的子矩阵,其内部的相对坐标为 \((i,j)\)(\(i,j\) 从 \(0\) 到 \(len-1\))。
- 顺时针旋转:目标位置 \((i,j)\) 的元素,来自源矩阵的 \((len-1-j,i)\) 位置。
- 逆时针旋转:目标位置 \((i,j)\) 的元素,来自源矩阵的 \((j,len-1-i)\) 位置。
参考代码
#include <cstdio>
using namespace std;
// a 是主矩阵,tmp 是用于旋转的临时辅助矩阵
int a[505][505], tmp[505][505];
int n; // 矩阵大小
/**
* @brief 打印整个矩阵 a
*/
void print() {
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= n; ++j)
printf("%d ", a[i][j]);
printf("\n");
}
}
/**
* @brief 将矩阵 a 中指定的方形子区域旋转90度
*
* @param x 子区域左上角的行号
* @param y 子区域左上角的列号
* @param len 子区域的边长
* @param d 旋转方向 (0: 顺时针, 1: 逆时针)
*/
void rotate(int x, int y, int len, int d) {
// 步骤1: 将 a 中旋转后的结果存入临时矩阵 tmp
// 遍历子区域中的每一个目标位置 (使用相对坐标 i, j)
for (int i = 0; i < len; ++i) {
for (int j = 0; j < len; ++j) {
if (d == 1) { // 逆时针旋转
// 目标位置 (x+i, y+j) 的元素来自源位置 (x+j, y+len-1-i)
tmp[x + i][y + j] = a[x + j][y + len - 1 - i];
} else { // 顺时针旋转
// 目标位置 (x+i, y+j) 的元素来自源位置 (x+len-1-j, y+i)
tmp[x + i][y + j] = a[x + len - 1 - j][y + i];
}
}
}
// 步骤2: 将临时矩阵 tmp 中的旋转结果写回到主矩阵 a
for (int i = 0; i < len; ++i) {
for (int j = 0; j < len; ++j) {
a[x + i][y + j] = tmp[x + i][y + j];
}
}
}
int main()
{
int m; // 魔法施放次数
scanf("%d%d", &n, &m);
// 初始化矩阵,从1到n*n顺序填充
int cnt = 0;
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= n; ++j) {
a[i][j] = ++cnt;
}
}
// 执行 m 次旋转操作
for (int i = 0; i < m; i++) {
int x, y, r, z;
scanf("%d%d%d%d", &x, &y, &r, &z);
// 将中心点(x,y)和半径r 转换为 左上角坐标和边长
int start_x = x - r;
int start_y = y - r;
int len = 2 * r + 1;
rotate(start_x, start_y, len, z);
}
// 打印最终结果
print();
return 0;
}
习题:P1328 [NOIP2014 提高组] 生活大爆炸版石头剪刀布
解题思路
游戏有 5 种手势,两两组合的胜负关系是固定的。如果每次都用 if-else 判断,代码会非常繁琐。最高效的方法是预先创建一个 5×5 的二维数组,作为胜负关系的“查找表”。
小 A 和小 B 的出拳序列是重复的,周期长度分别为 \(N_A\) 和 \(N_B\)。要得到第 \(i\) 轮(\(i\) 从 \(0\) 开始)的出拳手势,可以使用取模运算来定位到它们各自规律数组中的正确位置。小 A 的第 \(i\) 轮出拳是 \(A_{i \bmod N_A}\),小 B 的第 \(i\) 轮出拳是 \(B_{i \bmod N_B}\),这个方法简洁地实现了周期的循环。
这种“查表法 + 循环取模”的组合是解决此类周期性模拟问题的经典高效方案。
参考代码
#include <cstdio>
// 预先计算好的得分矩阵 (Lookup Table)
// res[A的出拳][B的出拳] 的结果是从A的视角来看的
// 0:剪刀, 1:石头, 2:布, 3:蜥蜴人, 4:斯波克
// 结果: 1 表示A赢, -1 表示A输(B赢), 0 表示平局
int res[5][5] = {
{0, -1, 1, 1, -1}, // A出剪刀 vs B出(剪刀, 石头, 布, 蜥蜴人, 斯波克)
{1, 0, -1, 1, -1}, // A出石头 vs B出(...)
{-1, 1, 0, -1, 1}, // A出布 vs B出(...)
{-1, -1, 1, 0, 1}, // A出蜥蜴人 vs B出(...)
{1, 1, -1, -1, 0} // A出斯波克 vs B出(...)
};
// a, b 分别存储小A和小B的出拳周期规律
int a[205], b[205];
int main()
{
int n, na, nb; // n:总轮数, na:小A周期长度, nb:小B周期长度
scanf("%d%d%d", &n, &na, &nb);
// 读取小A和小B的出拳规律
for (int i = 0; i < na; ++i) scanf("%d", &a[i]);
for (int i = 0; i < nb; ++i) scanf("%d", &b[i]);
// sa, sb 分别记录小A和小B的得分
int sa = 0, sb = 0;
// 主循环,模拟从第0轮到符n-1轮的比赛
for (int i = 0; i < n; ++i) {
// a[i % na] -> 使用取模运算获取小A在符i轮的出拳
// b[i % nb] -> 使用取模运算获取小B在符i轮的出拳
int r = res[a[i % na]][b[i % nb]];
// 根据查表结果更新分数
if (r == 1) { // A赢了
++sa;
} else if (r == -1) { // B赢了
++sb;
}
// r == 0 是平局,两人都不得分
}
// 输出最终得分
printf("%d %d\n", sa, sb);
return 0;
}
习题:P1067 [NOIP2009 普及组] 多项式输出
解题思路
多项式的最高次项系数可能为零,因此,必须先从左到右(从高次到低次)找到第一个系数不为零的项。这个项是实际输出的“第一项”,它的输出规则(特别是符号)与后续项不同。同时,这个过程也处理了一个特殊情况:如果所有系数都为零,则直接输出 0 即可。
每一项的输出都可以分成三步:
- 输出符号
- 首项:只有当其系数为负时,才在最前面输出
-。 - 非首项:根据系数的正负,输出
+与-作为连接符。
- 首项:只有当其系数为负时,才在最前面输出
- 输出系数
- 这是一个核心规则:只有当系数的绝对值不为 1,或者该项是常数项时,才输出系数的绝对值。
- 这意味着,当一个项的系数是 +1 或 -1 并且它不是常数项(即带有
x)时,数字1会被省略。
- 输出变量和指数
- 常数项:不输出任何与
x相关的内容。 - 一次项:只输出
x,不输出^1。 - 更高次项:输出
x^k的形式。
- 常数项:不输出任何与
参考代码
#include <cstdio>
#include <cmath> // 用于 abs 函数
using namespace std;
// 数组 a 用于存储多项式的系数
// a[i] 对应的是 x^(n-i) 项的系数
int a[105];
int main()
{
int n; // 多项式的最高次数
scanf("%d", &n);
// 读取 n+1 个系数,从 a[0] (x^n的系数) 到 a[n] (常数项的系数)
for (int i = 0; i <= n; ++i) {
scanf("%d", &a[i]);
}
// 1. 寻找第一个非零系数的项,它的索引记为 bg (begin)
int bg = 0;
while (bg <= n && a[bg] == 0) {
++bg;
}
// 边界情况:如果所有系数都为0,则输出 0
if (bg == n + 1) {
printf("0");
return 0;
}
// 2. 从第一个非零项开始遍历,直到常数项
for (int i = bg; i <= n; ++i) {
// 如果当前项系数为0,则跳过不输出
if (a[i] == 0) continue;
// --- 步骤 2.1: 处理符号 ---
if (i != bg) { // 如果不是第一项
if (a[i] > 0) {
printf("+"); // 系数为正,用+连接
} else {
printf("-"); // 系数为负,用-连接
}
} else { // 如果是第一项
if (a[i] < 0) {
printf("-"); // 只有系数为负时,才在最前面输出负号
}
}
// --- 步骤 2.2: 处理系数 ---
// 规则:当系数的绝对值不为1,或者该项是常数项(i==n)时,才输出系数的绝对值
// 换言之,只有当系数为+/-1且不是常数项时,才省略"1"
if (abs(a[i]) != 1 || i == n) {
printf("%d", abs(a[i]));
}
// --- 步骤 2.3: 处理变量和指数 ---
if (i < n) { // 只要不是常数项,就有可能输出x
if (i == n - 1) { // 如果是1次项 (x^1)
printf("x");
} else { // 如果是高于1次的项
printf("x^%d", n - i);
}
}
}
return 0;
}
习题:P1098 [NOIP2007 提高组] 字符串的展开
解题思路
阅读题意可以发现,如果一个字符不是减号,最终就原样保留在结果中。如果一个字符是减号,则进入一个复杂的判断和处理流程。
当处理到一个减号时,应该先按照题意做一系列的检查工作,检查是否满足展开条件。如果不满足展开条件,需要将这个减号原封不动地拼接到结果中。如果满足所有的展开条件,再根据三个参数生成一个替换的字符串。
参考代码
#include <cstdio>
#include <iostream>
#include <string>
using std::string;
using std::cin;
using std::cout;
bool islower(char ch) { // 辅助函数:判断字符是否为小写字母
return ch >= 'a' && ch <= 'z';
}
bool isdigit(char ch) { // 辅助函数:判断字符是否为数字字符
return ch >= '0' && ch <= '9';
}
int main() {
int p1,p2,p3; // 三个控制参数
string s; // 输入的待处理字符串
cin>>p1>>p2>>p3>>s; // 读取三个参数和字符串
int len = s.size();
string ans = ""; // 用于存储最终结果的字符串
for (int i = 0; i < len; i++) { // 主循环:遍历输入字符串的每一个字符
if (s[i] != '-') { // 如果当前字符不是减号,直接拼接到结果字符串中
ans += s[i];
} else { // 处理减号的情况
// 检查是否能够展开?题目条件:
// 减号两侧同为小写字母或同为数字,
// 且按照 ASCII 码的顺序,减号右边的字符严格大于左边的字符。
string tmp="-"; // 表示默认情况下加减号
char l=s[i-1], r=s[i+1]; // 获取减号左右两边的字符
// 检查是否满足展开条件
if (i-1>=0 && i+1<len) { // 1. 得有两侧(减号不能在字符串的开头或结尾)
if (islower(l)&&islower(r) || isdigit(l)&&isdigit(r)) { // 2. 两侧同为小写字母或同为数字
if (l < r) { // 3. 且右边字符的ASCII码严格大于左边
// 符合展开条件,具体展开
tmp = ""; // 从空字符串开始
// 展开的字符实际上是s[i-1]+1~s[i+1]-1
// 根据 p3 判断展开方向
if (p3==2) { // 逆序展开
for (char ch=r-1;ch>=l+1;ch--) { // 循环范围是从右边字符的前一个,到左边字符的后一个
// 错误写法:直接让ch表达要加的字符
// 这样会破坏循环过程
// 正确方式:单独用一个变量表示加什么字符
// 确定要填充的字符样式
char add=ch;
if (p1==3) add='*'; // p1=3,填充星号
if (p1==2 && islower(add)) add-=32; // p1=2,字母转大写
for (int j=1; j<=p2; j++) tmp+=add; // 根据 p2 重复填充字符
}
} else { // p3=1,顺序展开
for (char ch=l+1;ch<=r-1;ch++) { // 循环范围是从左边字符的后一个,到右边字符的前一个
// 确定要填充的字符样式
char add=ch;
if (p1==3) add='*'; // p1=3,填充星号
if (p1==2 && islower(add)) add-=32; // p1=2,字母转大写
for (int j=1; j<=p2; j++) tmp+=add; // 根据 p2 重复填充字符
}
}
}
}
}
ans += tmp; // 将处理好的部分(无论是单个减号还是展开的字符串)拼接到最终结果中
}
}
cout<<ans<<"\n"; // 输出最终的展开后字符串
return 0;
}
习题:P1518 [USACO2.4] 两只塔姆沃斯牛 The Tamworth Two
解题思路
核心问题:如何判断农夫和牛“永远不会相遇”?
当整个系统进入一个之前已经出现过的状态时,就意味着它们陷入了一个无限循环。因为移动规则是确定的,一旦状态重复,后续的所有移动轨迹也将无限重复。既然在这个循环中它们没有相遇,那么它们就永远不会相遇了。
如何定义整个系统的“状态”?在任何一个时间点,要完全描述系统的情况,需要知道:牛的位置、牛的朝向、农夫的位置、农夫的朝向,可以用一个多维布尔数组来记录某个系统状态是否已经出现过。
参考代码
#include <cstdio>
const int N = 15; // 数组大小设为15,方便使用1-10的坐标,防止越界
// 定义方向增量:0:上(北),1:右(东),2:下(南),3:左(西)
// 顺序是顺时针,方便转向计算
int dx[4] = {-1, 0, 1, 0}; // 行变化
int dy[4] = {0, 1, 0, -1}; // 列变化
char a[N][N]; // 存储地图
// vis数组用于记录状态是否出现过,以检测循环
// 维度分别代表:牛x,牛y,牛方向,农夫x,农夫y,农夫方向
bool vis[N][N][4][N][N][4];
bool valid(int x, int y) { // 验证坐标(x,y)是否有效(是否可以移动到该位置)
// 在地图范围内 + 不是障碍物
// 注意不能用空地来判断,因为一开始牛和John的位置也能走
return x >= 1 && x <= 10 && y >= 1 && y <= 10 && a[x][y] != '*';
}
int main()
{
// 读取地图,注意 scanf("%s", a[i] + 1) 是为了将字符串读入到从第1列开始的位置
for (int i = 1; i <= 10; i++) {
scanf("%s", a[i] + 1);
}
// 初始化牛和农夫的坐标和方向
int x_cow, y_cow, d_cow = 0; // 初始方向为0(北)
int x_farmer, y_farmer, d_farmer = 0; // 初始方向为0(北)
for (int i = 1; i <= 10; i++) {
for (int j = 1; j <= 10; j++) {
// 寻找牛和John的初始位置
if (a[i][j] == 'C') {
x_cow = i; y_cow = j;
}
if (a[i][j] == 'F') {
x_farmer = i; y_farmer = j;
}
}
}
vis[x_cow][y_cow][0][x_farmer][y_farmer][0] = true; // 标记初始状态为已访问
int ans = 0; // 记录经过的分钟数
while (true) { // 主循环模拟
ans++; // 时间流逝一分钟
// 模拟牛的移动
// 计算牛前方的目标格子
int x = x_cow + dx[d_cow];
int y = y_cow + dy[d_cow];
if (valid(x, y)) { // 如果前方可达
x_cow = x; y_cow = y; // 移动
} else {
d_cow = (d_cow + 1) % 4; // 否则,顺时针转向
}
// 模拟农夫的移动
// 计算农夫前方的目标格子
x = x_farmer + dx[d_farmer];
y = y_farmer + dy[d_farmer];
if (valid(x, y)) { // 如果前方可达
x_farmer = x; y_farmer = y; // 移动
} else {
d_farmer = (d_farmer + 1) % 4; // 否则,顺时针转向
}
// 检查终止条件
// 1. 相遇
if (x_farmer == x_cow && y_farmer == y_cow) {
break; // 追捕成功,跳出循环
}
// 2. 状态重复(陷入循环)
if (vis[x_cow][y_cow][d_cow][x_farmer][y_farmer][d_farmer]) {
// 说明这个局面之前已经出现过了,再继续走下去也只是重复
// 不可能再有机会相遇了
ans = 0; break; // 跳出循环
}
vis[x_cow][y_cow][d_cow][x_farmer][y_farmer][d_farmer] = true; // 还未相遇,标记当前状态为已访问
}
printf("%d\n", ans); // 输出最终结果
return 0;
}
习题:P1065 [NOIP2006 提高组] 作业调度方案
解题思路
对于每个工件,记录它已经完成了几道工序,以及它上一道工序的完成时刻。这个完成时刻是满足“工件约束”的关键,它代表了该工件下道工序可以开始的最早时刻。
对于每台机器,维护一个它所有空闲时间段的列表。例如,机器 1 可能在 \([0,5], [10, 18], [22, +\infty]\) 这些时间段是空闲的。当一个新的操作被安排时,它会占用并切分这些空闲的时间段。
参考代码
#include <cstdio>
#include <algorithm>
using namespace std;
const int INF = 1e9; // 用一个很大的数代表无穷大
// 数据存储
int seq[405]; // 存储输入的m*n个工件的安排顺序
int machine_id[25][25]; // machine_id[x][y]: 工件x的第y道工序在哪台机器上加工
int time_cost[25][25]; // time_cost[x][y]: 工件x的第y道工序的加工时间
// 状态变量
int finish[25]; // finish[x]: 工件x已完成多少道工序
int end_time[25]; // end_time[x]: 工件x上一道工序的完成时刻
// machine[x][y][0/1]: 机器x的第y个空闲时间段的 [开始时间, 结束时间]
// 这是一个核心数据结构,模拟了每台机器的空闲时间轴
int machine[25][25][2];
int sz[25]; // sz[x]代表机器x上有多少个空闲时间段
int main() {
int m, n;
scanf("%d%d", &m, &n);
// 初始化:每台机器最初只有一个从0到无穷大的空闲时间段
for (int i = 1; i <= m; i++) {
machine[i][1][0] = 0; // 开始时间
machine[i][1][1] = INF; // 结束时间
sz[i] = 1; // 空闲段数量为1
}
// 读取输入数据
for (int i = 0; i < m * n; i++) scanf("%d", &seq[i]);
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++) scanf("%d", &machine_id[i][j]);
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++) scanf("%d", &time_cost[i][j]);
int ans = 0; // 记录全局最晚时间
// 主模拟循环:按照给定的顺序处理每一个操作
for (int i = 0; i < m * n; i++) {
int cur = seq[i]; // 当前对哪个工件进行加工
int order = finish[cur] + 1; // 该工件即将进行第几道工序
int start_time = end_time[cur]; // 该工件在机器上至少要从哪个时刻开始可以加工
int mch_id = machine_id[cur][order]; // 该工件当前这道工序放在哪台机器上加工
int cost = time_cost[cur][order]; // 该工件当前这道工序所需的加工时间
// 寻找机器上符合要求的第一个可以用来加工的空闲时间段
for (int j = 1; j <= sz[mch_id]; j++) {
int bg = machine[mch_id][j][0], ed = machine[mch_id][j][1]; // 该空闲时间段为[bg,ed]
if (ed >= start_time) { // 至少要在start_time时刻之后
int available_time = ed - max(start_time, bg);
if (available_time >= cost) { // 该空闲时间段可用来加工
int occupy_bg = max(start_time, bg); // 计算在此空闲段中,实际可以开始的最早时间
int occupy_ed = occupy_bg + cost;
// 这次加工将占用[occupy_bg,occupy_ed]这个时间段
// 分类讨论:
// 1.[bg,ed]全用完;
// 2.[bg,ed]的前半段或后半段被占用;
// 3.[bg,ed]被拆成两段空闲时间
if (ed - bg == occupy_ed - occupy_bg) {
// 此时这个空闲时间段将在数组中消失,进行数组元素删除
for (int k = j; k < sz[mch_id]; k++) {
machine[mch_id][k][0] = machine[mch_id][k + 1][0];
machine[mch_id][k][1] = machine[mch_id][k + 1][1];
}
sz[mch_id]--;
} else if (occupy_bg == bg) {
// 此时直接更新这个空闲时间段的开始时间即可
machine[mch_id][j][0] = occupy_ed;
} else if (occupy_ed == ed) {
// 此时直接更新这个空闲时间段的终止时间即可
machine[mch_id][j][1] = occupy_bg;
} else {
// 此时[bg,ed]被拆成[bg,occupy_bg]和[occupy_ed,ed]
machine[mch_id][j][1] = occupy_bg;
// 将[occupy_ed+1,ed]插入到数组中
for (int k = sz[mch_id]; k > j; k--) {
machine[mch_id][k + 1][0] = machine[mch_id][k][0];
machine[mch_id][k + 1][1] = machine[mch_id][k][1];
}
machine[mch_id][j + 1][0] = occupy_ed;
machine[mch_id][j + 1][1] = ed;
sz[mch_id]++;
}
// 更新工件状态和全局答案
finish[cur]++; // 该工件完成的工序数+1
end_time[cur] = occupy_ed; // 更新该工件的最后完成时间
if (occupy_ed > ans) ans = occupy_ed; // 更新全局最晚完成时间
break; // 已成功安排,跳出对空闲段的搜索,处理下一个操作
}
}
}
}
printf("%d\n", ans);
return 0;
}
习题:P1022 [NOIP 2000 普及组] 计算器的改良
解题思路
解题的关键在于将方程的所有项通过移项,统一到等号的一边,形成 \(kx+c=0\) 的标准形式,然后计算出解 \(x = -c/k\)。
参考代码
#include <cstdio>
#include <iostream>
#include <string>
using std::string;
using std::cin;
int main()
{
string s;
cin >> s;
int len = s.length();
int i = 0; // 主指针,标记当前处理到的字符串位置
// k: 未知数的总系数 (Koeffizient)
// y: 常数项的总和
int k = 0, y = 0;
// sign: 方程左右边的符号。左边为1,右边为-1。用于模拟“移项”操作。
int sign = 1;
char x; // 存储未知数的字母
// 循环处理整个方程字符串
while (i < len) {
int j = i; // 临时指针,用于解析单个项
// flag: 当前项的符号 (+或-)
int flag = 1;
if (s[j] == '-') {
flag = -1;
j++;
} else if (s[j] == '+') {
flag = 1;
j++;
}
// 解析一个完整的项(数字和可能的变量)
int num = 0; // 当前项的数字部分
bool isx = false; // 标记当前项是否是未知数项
while (j < len) {
// 如果遇到运算符或等号,说明当前项结束
if (s[j] == '+' || s[j] == '-' || s[j] == '=') break;
if (s[j] >= '0' && s[j] <= '9') {
// 如果是数字,累加到num
num = num * 10 + s[j] - '0';
} else {
// 如果是字母,记录下来,并标记为未知数项
x = s[j];
isx = true;
}
j++;
}
// 特殊情况处理:如果一个项是未知数项但没有数字(如'x'或'-a')
// 此时num为0,需要强制设为1
if (num == 0 && isx) num = 1;
// 根据项的类型,累加到总系数k或总常数y
// 核心逻辑: 最终值 = 数值 * 项符号(flag) * 方程边符号(sign)
if (isx) {
k += num * flag * sign;
} else {
y += num * flag * sign;
}
// 判断当前项的结束位置
if (j < len && s[j] == '=') {
// 如果遇到'=',说明到了方程右边,将sign反转
sign = -1;
i = j + 1; // 主指针跳过'='
} else {
// 否则,主指针移动到当前项的末尾
i = j;
}
}
// 此时方程已化为 k*x + y = 0 的形式
// 解为 x = -y / k
// 使用 1.0 确保进行浮点数除法
printf("%c=%.3f\n", x, -1.0 * y / k);
return 0;
}
习题:P9979 [USACO23DEC] Target Practice S
解题思路
直接的暴力解法是:遍历 \(C\) 个命令中的每一个,对于每一个命令,尝试将它改成另外两种命令,然后对这 \(2C\) 种新的命令序列,完整地模拟一遍过程,记录最大命中数。这个复杂度是 \(O(C^2)\),对于 \(C=10^5\) 来说太慢了,需要一个更快的方法来评估“只改变一个命令”带来的影响。
观察一个改变带来的影响,如果在第 \(i\) 个位置,将一个命令(如 L)改成了另一个(如 R),那么从第 \(i\) 步开始,Bessie 的整个后续路径都将产生一个固定的偏移。
L -> R:后续路径整体向右偏移+2L -> F:后续路径整体向右偏移+1R -> L:后续路径整体向左偏移-2R -> F:后续路径整体向左偏移-1F -> L:后续路径整体向左偏移-1F -> R:后续路径整体向右偏移+1
所有的偏移量都在 \(\{ -2,-1,0,+1,+2 \}\) 这个集合里(\(0\) 代表不改变),可以想象存在 5 个“偏移世界”,在 \(k\) 世界里,Bessie 的每一步都比原路径偏移了 \(k\)。
可以从左到右遍历命令序列,在每一步 \(i\),快速计算出“如果改变 \(i\) 这个命令,最终能命中多少靶子”。为了能“快速计算”,需要预先知道一些信息,并在扫描过程中动态地更新这些信息。
在开始扫描之前,先对 5 个“偏移世界”进行一次完整的模拟。sum[k] 记录在偏移量为 k - 2 的世界里(k 从 0 到 4),整个命令序列走完能命中的不同靶子的总数。例如,sum[2] 就是原封不动执行命令能命中的靶子总数。cnt[k][pos] 记录在偏移量为 k - 2 的世界里,位置 pos 被 F 命令命中了多少次,这对于处理“靶子只能被摧毁一次”的规则至关重要。
由于坐标可能为负,给所有坐标加上一个 OFFSET(例如 100000),将它们映射到正整数数组下标。
遍历命令序列,假设要修改命令 \(i\),以从 F 修改到 L 为例:这个修改意味着,在这一步,放弃了在当前位置 pos 的一次开火机会。同时,整个后续路径都将向左偏移 -1。那么,总的命中数可以看作是在 -1 偏移世界里的总命中数减去因为本次修改而“意外”产生的重复命中。如果 pos 处有靶子,并且在 -1 世界里它只被命中了这一次(cnt[1][pos] == 1),那么这次 F -> L 的修改就使得这个靶子不再被命中,所以总数要减一。如果它被命中多次,那么这次修改不影响它最终还是会被命中的事实,总数不变。这是一个非常聪明的计算方式,它用全局预计算的结果加上一个局部修正来得到改变后的总分。其他类型的修改也用类似的逻辑进行计算。
在命令 \(i\) 计算完所有可能的修改带来的得分后,需要为 \(i+1\) 做准备。sum 和 cnt 数组需要被更新,以便它们能代表从 \(i+1\) 开始的后续序列在各个偏移世界中的命中情况。这个更新通过“撤销”命令 \(i\) 操作的影响来实现。如果命令 \(i\) 是 F,就遍历 5 个偏移世界,将 pos 在各个世界中对应的命中位置的 cnt 减一,如果 cnt 减到 0,说明这个靶子在后续序列中不再被命中,就将对应世界的 sum 减一。同时,根据当前命令更新 pos 的值,为下一次循环做准备。
所有计算过的得分的最大值就是最终答案。
参考代码
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 100005;
const int OFFSET = 100000; // 坐标偏移量,处理负坐标
// cnt[k][pos]:在偏移世界k-2中,位置pos被命中了多少次
// sum[k]:在偏移世界k-2中,总共命中了多少个不同的靶子
int cnt[5][N * 2], sum[5];
bool tar[N * 2]; // 标记靶子位置
char op[N]; // 存储命令序列
int main()
{
int t, c;
scanf("%d%d", &t, &c);
// 读取并标记靶子位置
for (int i = 1; i <= t; i++) {
int pos; scanf("%d", &pos);
tar[pos + OFFSET] = true;
}
scanf("%s", op);
// 模拟5个偏移世界{-2, -1, 0, 1, 2}的完整过程
for (int i = -2; i <= 2; i++) {
int pos = OFFSET; // 初始位置0
for (int j = 0; j < c; j++) {
char ch = op[j];
if (ch == 'L') pos--;
else if (ch == 'R') pos++;
else if (tar[pos + i]) { // 在偏移世界i中,实际命中的位置是 pos + i
if (cnt[i + 2][pos + i] == 0) sum[i + 2]++; // 如果这个靶子是第一次被命中,则总命中数+1
cnt[i + 2][pos + i]++; // 该位置的命中次数+1
}
}
}
int ans = sum[2]; // 初始答案为不作任何修改时的得分
int pos = OFFSET; // 当前位置
for (int i = 0; i < c; i++) {
char ch = op[i];
// 计算修改op[i]能得到的最大分数
if (ch == 'L') {
// 尝试修改 L->R:后续路径偏移+2,得分为偏移世界+2的得分
ans = max(ans, sum[4]);
// 尝试修改 L->F:在当前pos开火,后续路径偏移+1
// 得分为偏移世界+1的总分,如果当前位置有靶子且在+1世界里没被命中过,则额外+1
ans = max(ans, sum[3] + (cnt[3][pos] == 0 && tar[pos]));
} else if (ch == 'R') {
// 尝试修改 R->L:后续路径偏移-2
ans = max(ans, sum[0]);
// 尝试修改 R->F:在当前pos开火,后续路径偏移-1
ans = max(ans, sum[1] + (cnt[1][pos] == 0 && tar[pos]));
} else { // ch == 'F'
// 尝试修改 F->L:放弃本次开火,后续路径偏移-1
// 得分为偏移世界-1的总分,但如果本次开火是该靶子在-1世界中的唯一一次命中,则总分-1
ans = max(ans, sum[1] - (cnt[1][pos] == 1 && tar[pos]));
// 尝试修改 F->R:放弃本次开火,后续路径偏移+1
ans = max(ans, sum[3] - (cnt[3][pos] == 1 && tar[pos]));
}
// 更新状态,为下一个命令做准备
// 撤销当前命令操作对sum和cnt数组的影响,使它们代表后续序列的情况
if (ch == 'L') pos--;
else if (ch == 'R') pos++;
else { // ch == 'F'
for (int j = -2; j <= 2; j++) { // 遍历5个偏移世界
if (j == 0) continue;
// 在j世界中,本次F命中的是 pos+j,因此撤销在该处开的那枪
if (tar[pos + j]) {
if (cnt[j + 2][pos + j] == 1) sum[j + 2]--; // 如果本次命中是该靶子在j世界的最后一次命中,则总命中数-1
cnt[j + 2][pos + j]--; // 该位置命中次数-1
}
// 改为在pos处开了一枪
if (tar[pos]) {
if (cnt[j + 2][pos] == 0) sum[j + 2]++;
cnt[j + 2][pos]++;
}
}
}
}
printf("%d\n", ans);
return 0;
}
习题:P9804 [POI 2022/2023 R1] kol
解题思路
这是一个典型的模拟问题,核心的挑战在于如何高效地表示和更新蛇的状态。蛇的长度可以变得很长(最多 \(1+p\)),如果在每次移动时都更新蛇身上每个格子的坐标,当蛇很长时,单次移动的复杂度会是 \(O(\text{len})\),这里用 \(\text{len}\) 表示蛇的长度,这在 \(n\) 很大时会超时。
因此,需要一个更高效的方法来追踪蛇身的位置和内容:不直接存储蛇身每节的坐标,而是记录蛇头在每个时间点访问过的位置。
- 状态表示
- \(t_{w,k}\) 为一个 \(m \times m\) 的二维数组,用于记录蛇头在哪个时间戳访问了格子 \((w,k)\)。如果从未访问过,则为 0。
- \(\text{tm}\) 表示当前的时间戳,每次移动操作,\(\text{tm}\) 都会加一。
- \(\text{len}\) 表示蛇的当前长度。
- \(s_i\) 存储蛇身上第 \(i\) 节(从尾到头)的内容。
- \(b_{w,k}\) 存储 \((w,k)\) 处的食物值,-1 表示没有食物。
- 蛇身位置的判断:在任意时间戳 \(\text{tm}\),蛇的长度为 \(\text{len}\)。蛇头位于 \(\text{tm}\) 时刻访问的格子,蛇尾则位于 \(\text{tm} - \text{len} + 1\) 时刻访问的格子。因此,蛇身覆盖了所有在时间戳范围 \([\text{tm}-\text{len}+1,\text{tm}]\) 内被蛇头访问过的格子。对于一个查询 \((w,k)\),只需检查 \(t_{w,k}\) 的值:
- 如果 \(t_{w,k}=0\),说明蛇头从未到过这里,肯定不是蛇身。
- 如果 \(t_{w,k} \lt \text{tm}-\text{len}+1\),说明蛇头虽然到过这里,但时间太早,蛇尾已经滑过了这个格子,所以也不是蛇身。
- 否则,\(t_{w,k}\) 在 \([\text{tm}-\text{len}+1,\text{tm}]\) 范围内,说明格子 \((w,k)\) 正是蛇身的一部分。
- 蛇身内容的查询:如果确定 \((w,k)\) 是蛇身,需要找到其对应的内容。\(s\) 数组从尾到头存储了蛇身内容,\(s_1\) 是蛇尾,\(s_{\text{len}}\) 是蛇头。
- 蛇尾 \(s_1\) 对应的访问时间是 \(\text{tm}-\text{len}+1\)。
- 蛇头 \(s_{\text{len}}\) 对应的访问时间是 \(\text{tm}\)。
- 从尾部数第 \(j\) 节 \(s_j\) 对应的访问时间是 \(\text{tm}-\text{len}+j\)。
- 已知 \((w,k)\) 的访问时间是 \(T = t_{w,k}\),所以 \(T = \text{tm}-\text{len}+j\),解得 \(j = T - \text{tm} + \text{len}\)。因此,\((w,k)\) 对应的内容就是 \(s_{t_{w,k}-\text{tm}+\text{len}}\)。
- 移动与生长
- 移动:\(\text{tm}\) 加一,更新蛇头坐标 \((x,y)\),并记录 \(t_{x,y} = \text{tm}\)。
- 生长:如果移动到的新位置 \((x,y)\) 有食物(\(b_{x,y} \ne -1\)),则蛇身的长度 \(\text{len}\) 加一,并将食物的值存入新的蛇头 \(s_{len}\),然后将该位置的食物移除。
- 如果没有食物,\(\text{len}\) 不变。由于 \(\text{tm}\) 增加了,时间窗口 \([\text{tm}-\text{len}+1,\text{tm}]\) 向前滑动,旧的蛇尾 \(\text{tm}-\text{len}\) 时刻的位置自然地被排除在蛇身之外了,实现了蛇的移动效果。
参考代码
#include <cstdio>
#include <iostream>
using namespace std;
const int M = 2005;
const int N = 1e6 + 5;
// --- 全局变量 ---
int b[M][M]; // b[w][k]: 存储 (w,k) 处食物的数值, -1 表示没有食物
int t[M][M]; // t[w][k]: 存储蛇头访问 (w,k) 时的时间戳
int s[N]; // s[i]: 存储蛇身第 i 节(从尾到头1-indexed)的内容
int main()
{
int m, p, n; cin >> m >> p >> n;
// 初始化食物棋盘
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= m; j++) {
b[i][j] = -1;
}
}
for (int i = 1; i <= p; i++) {
int w, k, c; cin >> w >> k >> c;
b[w][k] = c;
}
// --- 蛇的初始状态 ---
int x = 1, y = 1; // x, y: 蛇头的当前坐标
int len = 1; // len: 蛇的当前长度
int tm = 1; // tm: 当前时间戳
t[x][y] = 1; // 记录初始位置的时间戳
s[1] = 0; // 蛇身第一节的初始内容为 0
// 检查初始位置是否有食物
if (b[1][1] != -1) {
s[1] = b[1][1]; // 如果有,则第一节内容变为食物值
b[1][1] = -1; // 移除食物
}
// --- 处理 n 个操作 ---
for (int i = 1; i <= n; i++) {
char ch; cin >> ch;
if (ch == 'Z') { // --- 查询操作 ---
int w, k; cin >> w >> k;
// 检查 (w,k) 是否是蛇身的一部分
// 条件1: t[w][k] == 0, 蛇头从未访问过
// 条件2: t[w][k] < tm - len + 1, 访问过但蛇尾已滑过
if (t[w][k] == 0 || t[w][k] < tm - len + 1) {
cout << -1 << "\n";
} else {
// 如果是蛇身,计算其在 ct 数组中的索引并输出内容
// 索引 j = t[w][k] - tm + len
cout << s[len - (tm - t[w][k])] << "\n";
}
} else { // --- 移动操作 ---
tm++; // 时间戳增加
// 根据指令更新蛇头坐标
if (ch == 'G') {
x--;
} else if (ch == 'D') {
x++;
} else if (ch == 'L') {
y--;
} else { // 'P'
y++;
}
t[x][y] = tm; // 记录新蛇头位置的时间戳
// 检查新位置是否有食物
if (b[x][y] != -1) {
s[++len] = b[x][y]; // 蛇长+1,新蛇头内容为食物值
b[x][y] = -1; // 移除食物
}
// 如果没有食物,len不变,蛇尾自然脱落(因为时间窗口滑动)
}
}
return 0;
}
习题:P7075 [CSP-S 2020] 儒略日
解题思路
这是一个复杂的大模拟题,核心是处理日期和不同历法规则的转换。由于 \(r\) 的值很大,逐天模拟肯定会超时。因此,必须采用“周期性跳转”的方法来加速计算。
首先,需要确定历法变更的关键时间点对应的儒略日 \(r\) 的值。
- 基准点:\(r=0\) 对应公元前 4713 年 1 月 1 日。
- 历法分界点:公元 1582 年 10 月 4 日。
通过计算,从公元前 4713 年 1 月 1 日到公元 1582 年 10 月 4 日,总共经过了 2299161 天,这意味着:
- 当 \(r \lt 2299161\) 时,日期在儒略日时期。
- 当 \(r \ge 2299161\) 时,日期在格里高利历时期。\(r=2299161\) 对应格里高利历的第一天,即 1582 年 10 月 15 日。
还需要儒略历时期内,公元前后分界点的数据:
- 从公元前 4713 年 1 月 1 日到公元前 1 年 12 月 31 日,总共有 1721424 天。
- 当 \(r \lt 1721424\) 时,日期在公元前。
- 当 \(r \ge 1721424\)(且 \(r \lt 2299161\))时,日期在公元后(儒略历时期)。
根据上述分析,可以将问题分解为三个主要部分来处理。
\(r \lt 1721424\)(公元前,儒略历)
- 起始日期为公元前 4713 年 1 月 1 日。
- 在儒略历中,每 4 年有 1 个闰年,构成一个 \(365 \times 3 + 366 = 1461\) 天的周期。
- 可以快速计算经过了多少个 4 年周期,从而大步推进年份。
- 对于不足一个周期的剩余天数,再逐年、逐月推算,最终确定日期。
\(1721424 \le r \lt 2299161\)(公元后,儒略历)
- 首先将 \(r\) 减去公元前时期的总天数 1721424,得到从公元 1 年 1 月 1 日开始算起的天数。
- 此时的儒略历闰年规则为:年份能被 4 整除,同样是 1461 天的 4 年周期。
- 采用与公元前部分相同的策略:先进行 4 年周期的跳转,再对余下的天数进行逐年、逐月推算。
\(r \ge 2299161\)(公元后,格里高利历)
- 首先将 \(r\) 减去儒略历时期的总天数 2299161,得到从 1582 年 10 月 15 日开始算起的天数。
- 为了方便利用周期,可以先单独处理 1582 年 10 月 15 日到 1599 年 12 月 31 日这段时间,将日期推进到 1600 年 1 月 1 日。
- 从 1600 年 1 月 1 日开始,格里高利历有了稳定的 400 年大周期。一个 400 年周期有 97 个闰年,共 146097 天。
- 可以计算经过了多少个 400 年大周期,从而实现年份的快速跳转。
- 对于不足 400 年的剩余天数,可以逐年循环处理。因为最多循环 400 次,所以不会超时。
- 最后,当年份确定后,再逐月推算,找到最终的月份和日期。
通过这种分段处理、大周期跳转的策略,可以高效地处理每个查询。
参考代码
#include <cstdio>
using ll = long long;
// 1582年10月15日到年底的剩余天数
const int DAYS_REM_1582 = (31 - 14) + 30 + 31;
// 每个月的天数(非闰年)
int DAYS_IN_MONTH[13] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
// 判断是否为闰年,根据不同时期规则判断
// 负数年份代表公元前
bool is_leap(int year) {
if (year < 0) { // 公元前,儒略历规则
return (-year) % 4 == 1;
} else if (year <= 1582) { // 公元后,1582年及以前,儒略历规则
return year % 4 == 0;
} else { // 1582年以后,格里高利历规则
return year % 400 == 0 || (year % 4 == 0 && year % 100 != 0);
}
}
void solve() {
ll r;
scanf("%lld", &r);
int year = 0;
// --- 第一阶段:处理儒略历时期 (r < 2299161) ---
if (r < 2299161) {
// 1.1 公元前时期 (r < 1721424)
if (r < 1721424) {
// 从公元前4713年开始,使用4年周期(1461天)快速跳转
year = -4713 + r / 1461 * 4;
} else { // 1.2 公元后儒略历时期
r -= 1721424; // 减去公元前总天数,从公元1年开始计算
// 从公元1年开始,使用4年周期(1461天)快速跳转
year = 1 + r / 1461 * 4;
}
r %= 1461; // 计算周期跳转后剩余的天数
}
// --- 第二阶段:处理格里高利历时期 (r >= 2299161) ---
else {
r -= 2299161; // 减去儒略历总天数,从1582年10月15日开始计算
year = 1582;
int month = 10, day = 15;
// 2.1 特殊处理1582年剩余时间
if (r < DAYS_REM_1582) {
day += r;
// 手动处理月、日进位
if (day > 31) {
day -= 31; month++;
if (day > 30) {
day -= 30; month++;
}
}
printf("%d %d %d\n", day, month, year);
return;
}
// 2.2 处理1583年到1599年
r -= DAYS_REM_1582;
year = 1583;
for (int y = 1583; y < 1600; y++) {
int days_this_year = is_leap(y) ? 366 : 365;
if (r < days_this_year) {
break;
}
r -= days_this_year;
year++;
}
// 2.3 从1600年开始,使用400年周期(146097天)快速跳转
if (r >= 146097) {
int num_400_years = r / 146097;
year += num_400_years * 400;
r %= 146097;
}
}
// --- 第三阶段:对周期跳转后的剩余天数进行逐年、逐月处理 ---
// 逐年递增,消耗剩余天数
while (true) {
int days_this_year = is_leap(year) ? 366 : 365;
if (r < days_this_year) break;
r -= days_this_year;
year++;
}
// 根据当年是否是闰年,更新二月天数
DAYS_IN_MONTH[2] = is_leap(year) ? 29 : 28;
// 逐月递增,确定月份和日期
for (int month = 1; month <= 12; month++) {
if (r < DAYS_IN_MONTH[month]) {
// 找到月份,输出结果
// r是0-indexed的天数,所以日期是r+1
printf("%lld %d %d", r + 1, month, year > 0 ? year : -year);
if (year < 0) printf(" BC"); // 如果是公元前,输出" BC"
printf("\n");
break;
}
r -= DAYS_IN_MONTH[month];
}
}
int main()
{
int q;
scanf("%d", &q); // 读取询问次数
while (q--) {
solve();
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号