倍增法
倍增法与二分法是“相反”的算法,二分法是每次缩小一半,从而以 \(O(\log n)\) 的速度快速缩小定位到解;倍增法是每次扩大一倍,从而以 \(O(2^n)\) 的速度快速地扩展到解空间。
倍增就是“成倍增长”,很多时候倍增的实现利用的是二进制本身的倍增特性。把一个数 \(n\) 用二进制展开,则 $n = a_0 \times 2^0 + a_1 \times 2^1 + a_2 \times 2^2 + a_3 \times 2^3 + a_4 \times 2^4 + \cdots $。例如 \(35\),它的二进制是 \(100011\),第 \(5\) 位、第 \(1\) 位和第 \(0\) 位为 \(1\),即 \(a_5=a_1=a_0=1\),把这几位的权值相加,得到 \(35=2^5+2^1+2^0=32+2+1\)。
二进制划分反映了一种快速增长的特性,第 \(i\) 位的权值 \(2^i\) 等于前面所有权值的和加 \(1\),即 \(2^i=2^{i-1}+2^{i-2}+\cdots+2^1+2^0+1\),一个整数 \(n\),它的二进制只有 \(\log n\) 位。如果要从 \(0\) 增长到 \(n\),可以以 \(1,2,4,\cdots,2^k\) 为“跳板”,快速跳到 \(n\),这些跳板只有 \(k = \log n\) 个。
倍增法的局限性是需要提前计算出第 \(1,2,4,\cdots,2^k\) 个跳板,这要求数据是静态不变的,不是动态变化的。如果数据发生了变化,那么所有跳板需要重新计算,跳板就失去了意义。
例题:P4155 [SCOI2015] 国旗计划
边境上有 \(m\) 个边防站围成一圈,顺时针编号为 \(1 \sim m\)。有 \(n\) 名战士,每名战士常驻两个站 \(c_i\) 和 \(d_i\),能在两个站之间移动。局长有一个“国旗计划”,让边防战士举着国旗环绕一圈。局长想知道至少需要多少战士才能完成“国旗计划”,并且他想知道在某个战士必须参加的情况下,至少需要多少名边防战士。
数据范围:\(n \le 2 \times 10^5, m < 10^9, 1 \le c_i,d_i \le m\)。
题目的要求很清晰:计算能覆盖整个圆圈的最少区间(战士)。
题目给定的所有区间互相不包含,那么按区间的左端点排序后,区间的右端点也是也是单调递增的。这种情况下能用贪心法选择区间。
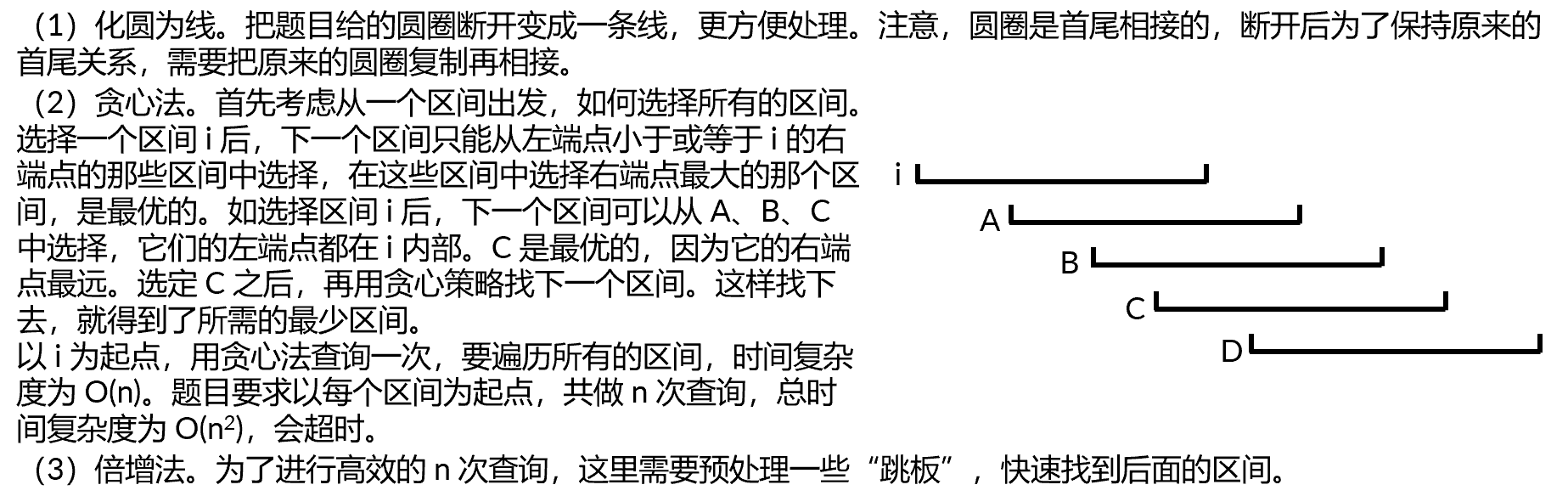
定义 \(go_{s,i}\) 表示从第 \(s\) 个区间出发,走 \(2^i\) 个最优区间后到达的区间。例如,\(go_{s,4}\) 是从 \(s\) 出发到达的第 \(2^4=16\) 个最优的区间,\(s\) 和 \(go_{s,4}\) 之间的区间也都是最优的。
预计算出从所有的区间出发的 \(go\),以它们为“跳板”,就能快速跳到目的地。
跳的时候先用大数再用小数。以从 \(s\) 跳到后面第 \(27\) 个区间为例:
- 从 \(s\) 跳 \(16\) 步,到达 \(s\) 后的第 \(16\) 个区间 \(f_1\);
- 从 \(f_1\) 跳 \(8\) 步,到达 \(f_1\) 后的第 \(8\) 个区间 \(f_2\);
- 从 \(f_2\) 跳 \(2\) 步到达 \(f_3\);
- 从 \(f_3\) 跳 \(1\) 步到达终点 \(f_4\)。

时间复杂度是多少?查询一次,用倍增法从 \(s\) 跳到终点的时间复杂度为 \(O(\log n)\)。共有 \(n\) 次查询,总时间复杂度为 \(O(n \log n)\)。
剩下的问题是如何快速预计算出 \(go\)。有非常巧妙的递推关系:\(go_{s,i}=go_{go_{s,i-1},i-1}\)。可以这样理解:
- \(go_{s,i-1}\)。从 \(s\) 起跳,先跳 \(2^{i-1}\) 步到区间 \(z=go_{s,i-1}\);
- \(go_{z,i-1}\)。再从 \(z\) 跳 \(2^{i-1}\) 步。
一共跳了 \(2^{i-1}=2^{i-1}=2^i\) 步,这样就实现了从 \(s\) 起跳,跳到 \(s\) 的第 \(2^i\) 个区间。
特别地,\(go_{s,0}\) 是 \(s\) 后第 \(2^0=1\) 个区间(用贪心法算出的下一个最优区间),\(go_{s,0}\) 是递推式的初始条件,从它递推出了其他的所有值。递推的计算量有多大?从任意 \(s\) 到末尾,最多有个 \(\log n\) 个 \(go_{s,\dots}\),所以只需要递推 \(O(\log n)\) 次。计算 \(n\) 个节点的 \(go\),共计算 \(O(n \log n)\) 次。
以上所有计算,包括预计算 \(go\) 和 \(n\) 次查询,总时间复杂度为 \(O(n \log n)\)。
#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long LL;
const int MAXN = 4e5 + 5;
struct Interval {
LL c, d; // c和d为战士的左右区间
int id; // id为战士的编号
bool operator<(const Interval& other) const {
return c < other.c;
}
};
Interval a[MAXN];
int go[MAXN][20], n, m, ans[MAXN];
void init() { // 贪心+预计算倍增
int nxt = 1;
for (int i = 1; i <= n; i++) { // 用贪心求每个区间的下一个最优区间
// 最优区间是有交集且右端点最大的区间
while (nxt <= n && a[nxt].c <= a[i].d) nxt++;
go[i][0] = nxt - 1; // 区间i的下一个区间
}
for (int i = 1; (1 << i) < n / 2; i++) // 倍增:i=1,2,4,8,...,共logn次
for (int s = 1; s <= n; s++) // 每个区间后第2的i次方个区间
go[s][i] = go[go[s][i - 1]][i - 1];
}
int calc(int x) { // 从第x个战士出发
int ret = 1, dest = a[x].c + m;
for (int i = 19; i >= 0; i--) { // 从最大的i开始找
int nxt = go[x][i];
if (nxt && a[nxt].d < dest) {
x = nxt; // 跳到新位置
ret += 1 << i; // 累加跳过的区间个数
}
}
return ret + 1;
}
int main()
{
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) {
scanf("%lld%lld", &a[i].c, &a[i].d);
a[i].id = i; // 记录战士的顺序
if (a[i].c > a[i].d) a[i].d += m; // 把环变成链
}
sort(a + 1, a + n + 1); // 按左端点排序
for (int i = 1; i <= n; i++) { // 拆环加倍成一条链
a[n + i].c = a[i].c + m;
a[n + i].d = a[i].d + m;
}
n *= 2;
init();
for (int i = 1; i <= n / 2; i++) ans[a[i].id] = calc(i); // 逐个计算每个战士
for (int i = 1; i <= n / 2; i++) printf("%d%c", ans[i], i * 2 == n ? '\n' : ' ');
return 0;
}
例题:P10455 Genius Acm
对于一组固定的 CPU,显然应该取最大的 \(m\) 个数和最小的 \(m\) 个数,最大和最小构成一对,次大和次小构成一对……,这样求出的 SPD 是所有情况中最大的。而为了让数列 \(P\) 分成的段数最少,每一段都应该在 SPD 不超过 \(k\) 的前提下,尽量包含更多的数。所以从头开始对 \(P\) 进行分段,让每一段尽量长,到达结尾时分成的段数就是答案。
于是,需要解决的问题为:当确定一个左端点 \(l\) 之后,右端点 \(r\) 在满足 \(P_l \sim P_r\) 的 SPD 值不超过 \(k\) 的前提下,最大能取到多少。
求长度为 \(n\) 的一段的 SPD 需要排序配对,时间复杂度为 \(O(n \log n)\)。当 SPD 上限 \(k\) 比较小时,如果在整个 \(l \sim n\) 的区间上二分右端点 \(r\),二分的第一步就需要检验总长度的一半这个级别的长度,而最终实际上 \(r\) 只能扩展一点点,这里有大量的时间浪费。
可以考虑倍增的过程,依次尝试 \(1, 2, 4, 8, \dots\) 这样的长度,找到最长可延伸的 \(2\) 的幂的长度 \(t\),然后在其基础上继续考虑额外向右延伸 \(t/2, t/4, \dots\),最终找到精确的极限延伸长度。
这样的过程至多循环 \(O(\log n)\) 次,每次会对长为 \(r-l+1\) 的一段进行排序,而完成整个题目的求解累计的扩展长度为 \(n\),所以总体时间复杂度为 \(O(n \log^2 n)\)。实际上每次求 SPD 时可以不用直接对整段进行排序,而是采用类似归并排序的方法,只对新增的长度部分进行排序,然后合并新旧两段,这样总体时间复杂度可以降低到 \(O(n \log n)\)。
参考代码
#include <cstdio>
#include <algorithm>
using namespace std;
using ll = long long;
const int N = 5e5 + 5;
int n, m, p[N], tmp1[N], tmp2[N];
ll k;
// 一个标准的归并函数,用于合并两个已排序的子数组。
// 在 calc 函数中,它被用来合并两个部分:一个是之前已经排好序的部分,另一个是当前刚排序的新部分。
void merge(int l, int mid, int r) {
int i = l, j = mid + 1, k = l;
while (i <= mid && j <= r) {
if (tmp1[i] <= tmp1[j]) {
tmp2[k++] = tmp1[i++];
} else {
tmp2[k++] = tmp1[j++];
}
}
while (i <= mid) tmp2[k++] = tmp1[i++];
while (j <= r) tmp2[k++] = tmp1[j++];
for (int p = l; p <= r; p++) tmp1[p] = tmp2[p];
}
// calc 函数意图通过增量排序的方式来检查一个段 [l, r] 是否满足条件。
// l, r: 当前要检查的整个段的左右端点。
// len: 新加入的、未排序部分的长度。函数假设 [l, r-len] 部分的数据之前已经被排好序。
ll calc(int l, int r, int len) {
// 1. 将原始性能数据 p[l..r] 复制到临时数组 tmp1 中。
for (int i = l; i <= r; i++) {
tmp1[i] = p[i];
}
// 2. 只对新加入的部分 [r-len+1, r] 进行排序。
sort(tmp1 + (r - len + 1), tmp1 + r + 1);
// 3. 将已排序的旧部分 [l, r-len] 和刚排序的新部分 [r-len+1, r] 合并。
// 执行后,tmp1[l..r] 变为一个完整的有序数组。
merge(l, r - len, r);
ll sum = 0;
int cnt = 0;
// 4. 在排序后的数组上,从两端取值配对,计算最坏情况下的 SPD。
while (l <= r && cnt < m) {
sum += 1ll * (tmp1[l] - tmp1[r]) * (tmp1[l] - tmp1[r]);
l++; r--;
cnt++;
}
return sum;
}
void solve() {
scanf("%d%d%lld", &n, &m, &k);
for (int i = 1; i <= n; i++) {
scanf("%d", &p[i]);
}
// l 是当前段的起始位置, ans 是总分段数。
int l = 1, ans = 0;
// 贪心策略:只要还有CPU没被分段,就继续寻找下一个最长的段。
while (l <= n) {
// --- 寻找从 l 开始的最长有效段 ---
// 这个过程分为两步:倍增 和 精化。
// 步骤1: 倍增。快速尝试一个指数级增长的长度 len。
int len = 1;
while (l + len - 1 <= n) {
ll spd = calc(l, l + len - 1, len);
if (spd <= k) {
for (int i = l; i <= l + len - 1; i++) {
p[i] = tmp1[i];
}
len *= 2;
} else break;
}
// 步骤2: 精化。倍增停止时找到了一个有效长度 len/2 和一个无效长度 len。
// 在 [len/2, len) 的区间内继续考虑,找到精确的最长长度。
len /= 2;
int r = l + len - 1; // r 是当前已知有效的最远右端点
len /= 2;
while (len > 0) {
if (r + len > n) { // 防止越界
len /= 2;
continue;
}
ll spd = calc(l, r + len, len);
if (spd <= k) {
// 如果加上这段长度后仍然有效,则扩展右端点 r
r += len;
for (int i = l; i <= r; i++) {
p[i] = tmp1[i];
}
}
len /= 2;
}
// 找到了从 l 开始的最长有效段的右端点 r,下一个段从 r+1 开始。
l = r + 1;
ans++;
}
printf("%d\n", ans);
}
int main()
{
int t; scanf("%d", &t);
while (t--) solve();
return 0;
}
习题:P8251 [NOI Online 2022 提高组] 丹钓战
解题思路
先按题意模拟整个序列的入栈出栈过程。当由于一个新元素想要入栈而导致某元素被弹出时,则说明如果被弹出元素是入栈序列中的第一个元素,则它的下一个“成功的”元素是这个想要入栈的元素。因此可以预处理每一个元素的下一个“成功的”元素是谁以及相应的倍增跳跃表。对于每一个查询序列,利用倍增表就可以快速计算整个序列中“成功的”元素的数量。
参考代码
#include <cstdio>
#include <stack>
using std::stack;
const int N = 5e5 + 5;
const int LOG = 19;
int a[N], b[N], go[N][LOG];
int main()
{
int n, q; scanf("%d%d", &n, &q);
for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
for (int i = 1; i <= n; i++) scanf("%d", &b[i]);
stack<int> s;
for (int i = 1; i <= n; i++) {
while (!s.empty()) {
int pre = s.top();
int ta = a[pre], tb = b[pre];
if (a[i] != ta && b[i] < tb) break;
go[pre][0] = i; // 记录每个元素因为谁导致要弹出
s.pop();
}
s.push(i);
}
for (int i = 1; i < LOG; i++)
for (int j = 1; j <= n; j++)
go[j][i] = go[go[j][i - 1]][i - 1]; // 预处理倍增表
while (q--) {
int l, r; scanf("%d%d", &l, &r);
int ans = 0;
int cur = l;
for (int i = LOG - 1; i >= 0; i--)
if (go[cur][i] != 0 && go[cur][i] <= r) { // 向右跳但没有越过边界
// 跳了2的i次方步
ans += 1 << i; cur = go[cur][i];
}
printf("%d\n", ans + 1); // 要算上起点本身
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号