树状数组

树状数组（Binary Indexed Tree，BIT）是一种用于维护 $n$ 个元素的前缀信息的数据结构。

以前缀和为例，对于数列 $a$ ，可以将其存储为前缀和数组 $s$ 的形式，其中 $s_{i} = \sum_{j = 1}^{i} a_{j}$ 。那么通过前缀和数组，就可以快速求出原数组中给定区间中数字的和：对于区间 $[l, r]$ ，区间和为 $s_{r} - s_{l - 1}$ ，其中假设 $s_{0} = 0$ 。

显然，对于长度为 $n$ 的数列，前缀和需要用长度为 $n$ 的数组进行存储。而当数列 $a$ 发生变化时，要使得 $s$ 数组的内容仍能够正确对应数列 $a$ 的前缀和，就需要对 $s$ 的值进行修改，即使数列中只有一个数发生变化，也可能需要修改 $s$ 数组的多个值，才能保证整个数组仍然存储的是 $a$ 的前缀和。

类似地，对于长度为 $n$ 的数列，树状数组也会使用长度为 $n$ 的数组来进行存储。在这个数组中，每个位置存储的内容则稍微有些复杂。

例题：P3374 【模板】树状数组 1

已知一个数列，需要支持两种操作：
1. 将某一个数加上 $x$ ；
2. 求出某区间中每一个数的和并输出。
数列长度和操作个数均不超过 $5 \times 10^{5}$ 。

分析：如果使用朴素的做法，将这个数列保存在一个数组 $a$ 中，那么对于第二种操作，需要将查询区间内的每一个数依次加起来。如果这样做，那么最坏情况下每一次操作就要遍历整个数组，导致超时。

另一种想法是，通过将数列存储为前缀和数组 $s$ 的形式，那么就可以快速求出给定区间的和；然而，对于第一种操作，在最坏情况下则又需要修改整个数组，同样会导致超时。

那么有没有方法可以结合两种做法的优势，使得两个操作均使用较低的时间复杂度来完成呢？这里就可以用到树状数组。

对于任何一种数据结构，可以将其抽象为一个黑匣子：黑匣子里面存储的是数据，可以向其提供支持的操作，包括修改操作和查询操作。当向其支持查询操作时，其需要通过保存的数据计算出需要的结果然后返回；当向其提供修改操作时，黑匣子需要更新其内部的数据，来保证对于之后的查询操作，黑匣子仍能够返回正确的结果。能否解决问题取决于这个黑匣子是否能以及能以何种复杂度实现这些操作；而如何实现这样一个黑匣子，则是我们的任务。

在这个问题中，黑匣子需要维护一个数列，需要支持的有单点修改操作和区间查询操作。

和前缀和类似，树状数组每个位置保存的也是原数组中某一段区间的和。为了准确说明每个位置分别保存的是哪一段区间，首先引入一个函数 lowbit(x)，它的值是 $x$ 的二进制表达式中最低位的 $1$ 所对应的值。例如， $6$ 的二进制表示为 $(110)_{2}$ ，最低位的 $1$ 为第二个 $1$ ，其对应的值为 $(10)_{2} = (2)_{10}$ ，故 $l o w b i t (6) = 2$ ； $20$ 的二进制表示为 $(10100)_{2}$ ，最低位的 $1$ 为第二个 $1$ ，其对应的值为 $(100)_{2} = (4)_{10}$ ，故 $l o w b i t (20) = 4$ 。

在常见的计算机中，有符号数采用补码表示，而在补码表示下， $l o w b i t (x)$ 有一种简单的表达方法：lowbit(x)=x&(-x)，其中 & 为按位与。由于 $- x$ 的补码为 $x$ 按位取反后再加 $1$ ，考虑 $x$ 和 $- x$ 的二进制表示， $x$ 末尾的若干 $0$ 在取反后变成 $1$ ，加上 $1$ 后变成 $0$ ； $x$ 最低位的 $1$ 在取反后变成 $0$ ，得到进位后变成 $1$ ；比该位更高的不会得到进位，维持取反的状态。因此，在按位与的过程中，只有那一位得到的结果为 $1$ ，其余都为 $0$ 。

  x 二进制表示：0101...1000...0
-x 的反码表示：1010...0111...1
-x 的补码表示：1010...1000...0

那么，假设树状数组使用数组 $c$ 来进行存储，原来的 $n$ 个数分别为 $a_{1}$ 到 $a_{n}$ ，则 $c_{i} = \sum_{j = i - l o w b i t (i) + 1}^{i} a_{j}$ 。换句话说，树状数组中每个位置保存的是其向前 $l o w b i t$ 长度的区间和。

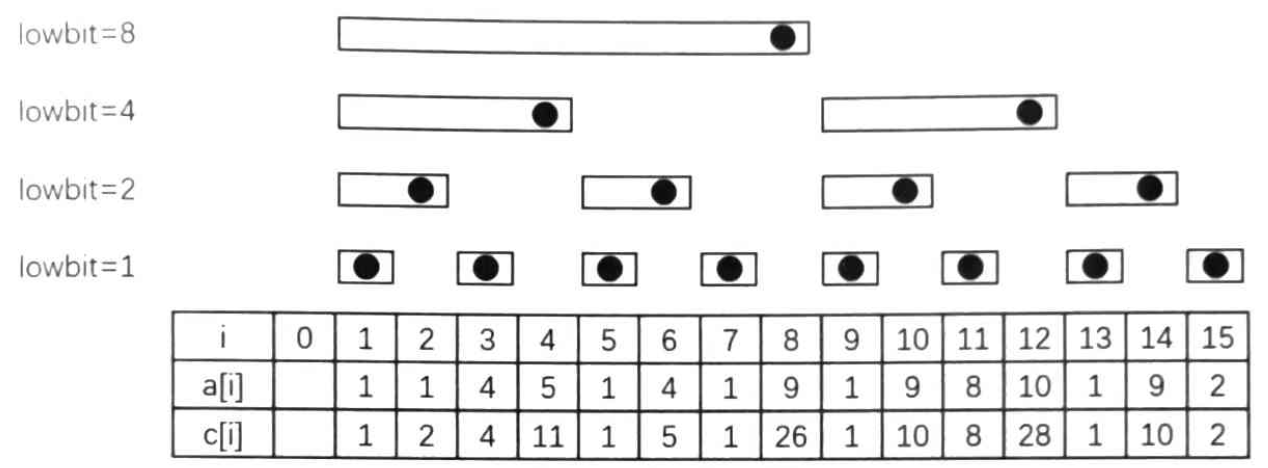
这样做有什么好处呢？考虑假设已经有了这样一个数组 $c$ ，如何用它实现前缀和查询操作。假设要求 $a_{1}$ 到 $a_{i}$ 的前缀和 $s_{i}$ ，可以先将 $c_{i}$ 加入答案，那么剩下的部分就是 $a_{1}$ 到 $a_{i - l o w b i t (i)}$ ，换句话说，问题变成了求 $s_{i - l o w b i t (i)}$ 。那么接下来又可以将 $c_{i - l o w b i t (i)}$ 加入答案，不断重复操作，直到问题变成求 $s_{0}$ 为止，那么此时就已经得到 $s_{i}$ 了。示例代码如下：

 int query(int x) {
	int res = 0;
	while (x > 0) {
		res += c[x]; x -= lowbit(x); // 从大到小将需要的值求和
	}
	return res;
}

这个过程的每一步中，把一个数 $x$ 变成 $x - l o w b i t (x)$ ，结合之前说的 $l o w b i t$ 的含义，可以发现实际上是在不断地去掉 $i$ 的二进制表示中最低位的 $1$ 。由于一个数 $i$ 的二进制表示的位数不超过 $\log i$ ，故每一次查询的时间复杂度为 $O (\log n)$ 。

接下来再考虑单点修改操作。假设修改的数是 $a_{i}$ ，由于可能有多个位置对应的区间包含 $a_{i}$ ，对于这些位置都要进行修改。

例如，要查询 $s_{14}$ 的值，可以发现 $s_{14} = c_{14} + c_{12} + c_{8} = 64$ ；如果要修改 $a_{3}$ 的值，则需修改所有包含 $a_{3}$ 的区间值，也就是 $a_{3}, a_{4}$ 和 $a_{8}$ 。

有哪些位置需要包含 $a_{i}$ 呢？先考虑几个结论，假设一个位置 $c_{j}$ 包含 $a_{i}$ ，那么有：

$j \geq i$ 。这一点很显然，因为一个位置只会包含它前面的数。
$l o w b i t (j) \geq l o w b i t (i)$ ，当且仅当 $j = i$ 时取等号。
$l o w b i t$ 的值相等的位置不会包含同一个数。

综合以上的结论，可以按 $l o w b i t$ 从小到大的顺序找出满足条件的 $j$ 。

首先， $i$ 是第一个满足条件的 $j$ ，记为 $j_{0} = i$ 。

下一个 $j$ 需要比 $i$ 大，且 $l o w b i t$ 也要更大，即二进制表示中末尾的 $0$ 更多，因此至少需要把最后一个 $1$ 变成 $0$ ，也就是至少加上 $l o w b i t (j_{0})$ ；由于 $l o w b i t (j_{0}) < l o w b i t (j_{0} + l o w b i t (j_{0}))$ ，而 $j_{0} = i$ ，所以 $i$ 显然在 $j_{0} + l o w b i t (j_{0})$ 对应的区间内，也就是说 $j_{0} + l o w b i t (j_{0})$ 就是下一个 $j$ ，记为 $j_{1} = j_{0} + l o w b i t (j_{0})$ 。

再下一个 $j$ 又可以通过 $j_{1} + l o w b i t (j_{1})$ 得到，由于 $l o w b i t$ 是翻倍增长的，所以 $l o w b i t (j_{0}) + l o w b i t (j_{1})$ 仍然小于 $l o w b i t (j_{1}) + l o w b i t (j_{1})$ ，意味着 $i$ 也在 $j_{1} + l o w b i t (j_{1})$ 所对应的区间内，即 $j_{2} = j_{1} + l o w b i t (j_{1})$ 。以此类推，即可得到所有需要修改的位置。示例代码如下：

 void add(int x, int y) {
	while (x <= n) {
		c[x] += y; x += lowbit(x); // 从小到大修改需要修改的位置
	}
}

由于 $l o w b i t$ 的值只有不超过 $\log n$ 种，一次修改中一个 $l o w b i t$ 值最多只会对应一个需要的位置，所以每一次修改的时间复杂度也为 $O (\log n)$ 。

至此，我们知道树状数组可以维护一个数列，并以 $O (\log n)$ 的时间复杂度进行单点修改操作和前缀和查询操作。对于本题，要实现的是区间和查询操作，可以通过前缀和查询操作来实现：对于 $[l, r]$ 的查询，只需要用 $[1, r]$ 的和减去 $[1, l - 1]$ 的和即可。

 #include <cstdio>
typedef long long LL;
const int MAXN = 5e5 + 5;
LL a[MAXN];
int n, m;
int lowbit(int x) {
    return x & -x;
}
LL query(int x) {
    LL ret = 0;
    while (x > 0) {
        ret += a[x];
        x -= lowbit(x);
    }
    return ret;
}
void update(int x, LL d) {
    while (x <= n) {
        a[x] += d;
        x += lowbit(x);
    }
}
int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++) {
        int x;
        scanf("%d", &x);
        update(i, x);
    }
    while (m--) {
        int op, x, y;
        scanf("%d%d%d", &op, &x, &y);
        if (op == 1) update(x, y);
        else printf("%lld\n", query(y) - query(x - 1));
    }
    return 0;
}

例题：P3368 【模板】树状数组 2

已知一个数列，需要进行两种操作：将区间 $[x, y]$ 每一个数加上 $x$ ；或者求出某一个数的值。
数列长度和操作个数均不超过 $5 \times 10^{5}$ 。

分析：和上个问题相反，这里需要对于数列实现区间加法的修改操作和单点的查询操作。乍一看好像没法使用树状数组，但实际上只需要进行一些小处理，就能把这个问题变得和上个问题相同。

对数组进行差分操作：假设原来的数列为 $a$ ，令 $b_{i} = a_{i} - a_{i - 1}$ ，那么 $a_{i} = \sum_{j = 1}^{i} b_{j}$ ，即 $a$ 是 $b$ 的前缀和数组。当 $b_{i}$ 增加 $x$ 时，意味着 $a_{i}$ 到 $a_{n}$ 都会增加 $x$ 。那么，对于 $b$ 数组而言，第一个操作的效果为：假设要将区间 $[l, r]$ 的数增加 $x$ ，则 $b_{l}$ 增加 $x$ ， $b_{r + 1}$ 减少 $x$ ；第二个操作的效果为：求出 $b$ 的某个前缀和。这样一来， $b$ 数组就可以用树状数组进行维护。

 #include <cstdio>
const int MAXN = 5e5 + 5;
int a[MAXN], n;
int lowbit(int x) {
    return x & -x;
}
int query(int x) {
    int ret = 0;
    while (x > 0) {
        ret += a[x];
        x -= lowbit(x);
    }
    return ret;
}
void update(int x, int d) {
    while (x <= n) {
        a[x] += d;
        x += lowbit(x);
    }
}
int main()
{
    int m, pre = 0;
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++) {
        int x;
        scanf("%d", &x);
        update(i, x - pre);
        pre = x;
    }
    while (m--) {
        int op;
        scanf("%d", &op);
        if (op == 1) {
            int x, y, k;
            scanf("%d%d%d", &x, &y, &k);
            update(x, k); update(y + 1, -k);
        } else {
            int x;
            scanf("%d", &x);
            printf("%d\n", query(x));
        }
    }
    return 0;
}

例题：P1908 逆序对

对于给定的一段正整数序列，逆序对就是序列中 $a_{i} > a_{j}$ 且 $i < j$ 的有序对。给定长度为 $n$ 的正整数序列，求逆序对数。其中 $n \leq 5 \times 10^{5}$ 。

分析：考虑朴素的做法，枚举 $i$ ，再枚举比 $i$ 大的位置 $j$ ，统计 $a_{j} < a_{i}$ 的数量。假设把所有 $j > i$ 中 $a_{j} = k$ 的数量记为 $c n t_{k}$ ，那么也就是统计 $s_{a_{i} - 1} = \sum_{k = 1}^{a_{i} - 1} c n t_{k}$ 。也就是说，查询的是一个数列 $c n t$ 的前缀和。如果按照从大到小的位置枚举 $i$ ，那么每当 $i$ 前进一步，可用的 $j$ 就增加一个，需要将 $c n t_{a_{j}}$ 增加 $1$ 。可以发现，这是不断地在对数列 $c n t$ 进行前缀和查询和单点修改操作，因此可以用树状数组维护数列 $c n t$ 。

但是还有一个问题：数列 $c n t$ 的长度是多少呢？由于 $a$ 中的元素可以很大，所以 $c n t$ 的下标也可以很大。为了解决这个问题，可以用到离散化的思想。由于 $c n t$ 数组开始时全为 $0$ ，总共会进行 $n$ 次修改，也就是说最多只有 $n$ 个位置不是 $0$ 。因此可以只记录这些可能非 $0$ 的位置。具体而言，首先将序列排序并去重，在这个序列上利用 std::lower_bound()，可以快速求出原数列中一个数是数列中的第几小。那么 $c n t_{k}$ 可以表示序列中第 $k$ 小的数的个数。这样一来， $c n t$ 的长度就最多是 $n$ 了。

 #include <cstdio>
#include <vector>
#include <algorithm>
using std::lower_bound;
using std::sort;
using std::unique;
using std::vector;
typedef long long LL;
const int N = 5e5 + 5;
int n, a[N], bit[N], bound;
vector<int> data;
int discretization(int x) { // 求出x是第几小
    return lower_bound(data.begin(), data.end(), x) - data.begin() + 1;
}
int lowbit(int x) {
    return x & -x;
}
void add(int x) {
    while (x <= bound) {
        bit[x]++; x += lowbit(x);
    }
}
int query(int x) {
    int res = 0;
    while (x > 0) {
        res += bit[x]; x -= lowbit(x);
    }
    return res;
}
int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) {
        scanf("%d", &a[i]); data.push_back(a[i]);
    }
    // 离散化的准备工作
    sort(data.begin(), data.end());
    data.erase(unique(data.begin(), data.end()), data.end());
    bound = data.size();
    LL ans = 0;
    for (int i = n; i >= 1; i--) {
        ans += query(discretization(a[i]) - 1);
        add(discretization(a[i]));
    }   
    printf("%lld\n", ans);
}

习题：P5459 [BJOI2016] 回转寿司

给定一个长度为 $n$ 的序列 $a$ ，从中选出一段连续子序列 $[l, r]$ ，使得 $L \leq \sum_{i = l}^{r} a_{i} \leq R$ ，求方案数。
数据范围： $1 \leq n \leq 10^{5}, | a_{i} | \leq 10^{5}, 1 \leq L, R \leq 10^{9}$ 。

解题思路

枚举 $r = 1 \sim x$ ，求出对于每个 $r$ 有多少 $l$ 符合条件，累加即为答案。

先预处理出前缀和数组 $s u m$ ，那么 $\sum_{i = l}^{r} a_{i}$ 的值为 $s u m_{r} - s u m_{l - 1}$ ，当且仅当 $L \leq s u m_{r} - s u m_{l - 1} \leq R$ 时 $l$ 符合条件。将式子变形，可得 $s u m_{r} - R \leq s u m_{l - 1} \leq s u m_{r} - L$ 。

所以只需要找到在 $r$ 前面有多少个 $s u m_{l - 1}$ 在 $[s u m_{r} - R, s u m_{r} - L]$ 这个值域范围内。这个问题可以对数据离散化后用树状数组维护，时间复杂度为 $O (n \log n)$ 。

参考代码

 #include <cstdio>
#include <algorithm>
#include <vector>
typedef long long LL;
using std::sort;
using std::lower_bound;
using std::unique;
using std::vector;
const int N = 1e5 + 5;
int a[N], bit[N * 3], bound;
LL sum[N];
vector<LL> data;
int discretization(LL x) {
    return lower_bound(data.begin(), data.end(), x) - data.begin() + 1;
} 
int lowbit(int x) {
    return x & -x;
} 
void add(int x) {
    while (x <= bound) {
        bit[x]++;
        x += lowbit(x);
    }
}
int query(int x) {
    int res = 0;
    while (x > 0) {
        res += bit[x];
        x -= lowbit(x);
    }
    return res;
}
int main()
{
    int n, l, r; scanf("%d%d%d", &n, &l, &r);
    data.push_back(0);
    for (int i = 1; i <= n; i++) {
        scanf("%d", &a[i]); sum[i] = sum[i - 1] + a[i]; // 预处理前缀和
        data.push_back(sum[i]);
        data.push_back(sum[i] - l);
        data.push_back(sum[i] - r);
    }
    sort(data.begin(), data.end());
    data.erase(unique(data.begin(), data.end()), data.end());
    bound = data.size();
    LL ans = 0;
    add(discretization(0)); // sum[0]计数加1
    for (int i = 1; i <= n; i++) { // 枚举右端点
        int q1 = query(discretization(sum[i] - l));
        int q2 = query(discretization(sum[i] - r) - 1);
        ans += q1 - q2; // 累加在值域范围内的方案数
        add(discretization(sum[i])); // sum[i]计数加1
    }
    printf("%lld\n", ans);
    return 0;
}

习题：P6186 [NOI Online #1 提高组] 冒泡排序

给定一个长度为 $n$ 的排列 $p$ ， $m$ 个操作，需要支持两种操作：交换 $p_{x}$ 和 $p_{x + 1}$ ；查询数组经过 $k$ 轮冒泡排序后的逆序对个数。
数据范围： $n, m \leq 2 \times 10^{5}; 1 \leq p_{i} \leq n$ 。

解题思路

设 $f_{i}$ 表示在数字 $i$ 左侧的比其大的数的个数，那么逆序对个数就是 $\sum_{i = 1}^{n} f_{i}$ 。

每经过一轮冒泡排序，若原本 $f_{i} > 0$ ，则一轮过后 $f_{i}$ 会减一，否则保持不变，即等于 $0$ 。想象一下一轮冒泡排序的过程：如果 $i$ 左边没有更大的数，则这个数左边的数不会跟它发生交换，则 $f_{i}$ 仍等于 $0$ ；如果左边有更大的数，则一轮冒泡过程中那个更大的数会和 $i$ 发生交换从而使得 $f_{i}$ 减一，并且在这一轮后面的过程中 $i$ 的位置就不变了。

由上可知，经过 $k$ 轮冒泡排序之后对逆序对还有贡献的是原本 $f_{i} > k$ 的数。则答案为 $(\sum_{f_{i} > k} f_{i}) - c n t \times k$ ，其中 $c n t$ 代表满足 $f_{i} > k$ 的 $i$ 的个数。这正好是两种不同的前缀和（ $f_{i}$ 的前缀和以及 $f_{i}$ 的个数的前缀和），可以通过树状数组维护。

针对交换操作，如果左小右大，则左边那个数对应的 $f$ 在交换后会加一，如果左大右小，则右边那个数对应的 $f$ 在交换后会减一，将其转化为相应树状数组上的更新操作即可。

参考代码

 #include <cstdio>
#include <algorithm>
using std::swap;
using std::min;
typedef long long LL;
const int N = 2e5 + 5;
int n, p[N], f[N];
// 树状数组inv用于求一开始的f[i]
// 树状数组cnt用于维护f[i]的个数的前缀和
// 树状数组sum用于维护f[i]的前缀和
LL sum[N], cnt[N], inv[N];
int lowbit(int x) {
    return x & -x;
}
void update(LL bit[], int x, int delta) {
    while (x <= n) {
        bit[x] += delta; x += lowbit(x);
    }
}
LL query(LL bit[], int x) {
    LL res = 0;
    while (x > 0) {
        res += bit[x]; x -= lowbit(x);
    }
    return res;
}
int main()
{
    int m; scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++) {
        scanf("%d", &p[i]);
        f[p[i]] = query(inv, n) - query(inv, p[i]);
        if (f[p[i]] > 0) {
            update(sum, f[p[i]], f[p[i]]);
            update(cnt, f[p[i]], 1);
        }
        update(inv, p[i], 1);
    }
    while (m--) {
        int t, c; scanf("%d%d", &t, &c);
        if (t == 1) {
            int i = p[c] < p[c + 1] ? p[c] : p[c + 1];
            // 注意不要忘了判f[i]>0
            if (f[i] > 0) {
                update(sum, f[i], -f[i]);
                update(cnt, f[i], -1);
            }
            f[i] += p[c] < p[c + 1] ? 1 : -1;
            if (f[i] > 0) {
                update(sum, f[i], f[i]);
                update(cnt, f[i], 1);
            }
            swap(p[c], p[c + 1]);
        } else {
            c = min(c, n - 1); // 冒泡排序n-1轮过后足够完成排序
            LL ans = query(sum, n) - query(sum, c) - (query(cnt, n) - query(cnt, c)) * c;
            printf("%lld\n", ans);
        }
    }
    return 0;
}

树状数组优化 DP

如果将树状数组代码中的求和改为取 max 或取 min，则树状数组可以用来维护前缀最大或最小值，从而帮助优化一些 DP 问题。

例题：P3431 [POI 2005] AUT-The Bus

在一个二维平面上给定 $k$ 个点，每个点有一个坐标 $(x, y)$ 以及点权 $p$ ，从左下角 $(1, 1)$ 走到右上角 $(n, m)$ ，只能向上或向右走，求经过的点权和的最大值， $k \leq 10^{5}$ 。

解题思路

若某个点为点 $i$ ，设 $d p_{i}$ 表示 $(1, 1)$ 到 $(x_{i}, y_{i})$ 点权和的最大值，则有 $d p_{i} = max {d p_{j}} + p_{i}$ ，其中点 $j$ 需要满足 $x_{j} \leq x_{i}$ 并且 $y_{j} \leq y_{i}$ ，也就是点 $j$ 在点 $i$ 的左下方。

为了保证计算某个点 $i$ 时其左下方的所有点都已计算过，可以对输入的点以横坐标为第一关键字，纵坐标为第二关键字进行排序，则排序后按顺序扫描即满足之前的点一定是在左边的。此时要求出该点下方（即 $y_{j} \leq y_{i}$ ）的 $d p_{j}$ 的最大值，正好是一个前缀最大值，所以可以用树状数组来维护。

时间复杂度 $O (k \log k)$ 。

参考代码

 #include <cstdio>
#include <algorithm>
#include <vector>
using ll = long long;
const int K = 100005;
struct Point {
    int x, y, p;
};
Point a[K];
int k;
ll c[K], dp[K];
std::vector<int> num;
int discretize(int x) {
    return std::lower_bound(num.begin(), num.end(), x) - num.begin() + 1;
}
int lowbit(int x) {
    return x & -x;
}
void update(int x, ll val) {
    while (x <= k) {
        c[x] = std::max(c[x], val);
        x += lowbit(x);
    }
}
ll query(int x) {
    ll res = 0;
    while (x > 0) {
        res = std::max(res, c[x]);
        x -= lowbit(x);
    }
    return res;
}
int main()
{
    int n, m; scanf("%d%d%d", &n, &m, &k);
    for (int i = 1; i <= k; i++) {
        scanf("%d%d%d", &a[i].x, &a[i].y, &a[i].p);
        num.push_back(a[i].y);
    }
    std::sort(num.begin(), num.end());
    num.erase(std::unique(num.begin(), num.end()), num.end());
    std::sort(a + 1, a + k + 1, [](const Point& lhs, const Point& rhs) {
        return lhs.x != rhs.x ? lhs.x < rhs.x : lhs.y < rhs.y;
    });
    ll ans = 0;
    for (int i = 1; i <= k; i++) {
        a[i].y = discretize(a[i].y);
        dp[i] = query(a[i].y) + a[i].p;
        ans = std::max(ans, dp[i]);
        update(a[i].y, dp[i]);
    }
    printf("%lld\n", ans);
    return 0;
}

习题：P6007 [USACO20JAN] Springboards G

在一个二维平面上给定 $p$ 对点，每对点有坐标 $(x_{1}, y_{1})$ 和 $(x_{2}, y_{2})$ ，表示从前者可以不需要行走瞬移到后者，从左下角 $(0, 0)$ 走到右上角 $(n, n)$ ，只能向上或向右走，求最小的行走距离， $p \leq 10^{5}$ 。

解题思路

设到点 $i$ 的最小行走距离是 $d p_{i}$ ，则有 $d p_{i} = min {d p_{j} + x_{i} - x_{j} + y_{i} - y_{j}}$ ，其中 $j$ 在 $i$ 的左下方。在计算 $d p_{i}$ 时， $x_{i}$ 和 $y_{i}$ 是两个定值，可以拆到括号外面，也就是 $d p_{i} = min {d p_{j} - x_{j} - y_{j}} + x_{i} + y_{i}$ ，于是和上一题类似，只不过相当于需要维护 $d p - x - y$ 的最小值。

而如果点 $i$ 是跳板的右上端点，还有一种情况是 $d p_{i} = d p_{j}$ ，这里的点 $j$ 指的是该跳板的左下端点。

为了在点排序后能维持之前的跳板关系，可以使用索引排序。

时间复杂度 $O (p \log p)$ 。

参考代码

 #include <cstdio>
#include <vector>
#include <algorithm>
using ll = long long;
const int P = 200005;
int n, p, x[P], y[P], idx[P], from[P];
ll c[P], dp[P];
std::vector<int> num;
int discretize(int x) {
    return std::lower_bound(num.begin(), num.end(), x) - num.begin() + 1;
}
int lowbit(int x) {
    return x & -x;
}
void update(int x, ll val) {
    while (x <= 2 * p) {
        c[x] = std::min(c[x], val);
        x += lowbit(x);
    }
}
ll query(int x) {
    ll res = 2 * n;
    while (x > 0) {
        res = std::min(res, c[x]);
        x -= lowbit(x);
    }
    return res;
}
int main()
{
    scanf("%d%d", &n, &p);
    for (int i = 1; i <= p; i++) {
        int x1, y1, x2, y2;
        scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
        x[i] = x1; y[i] = y1;
        x[i + p] = x2; y[i + p] = y2; from[i + p] = i;
        num.push_back(y1); num.push_back(y2);
        idx[i] = i; idx[i + p] = i + p;
    }
    std::sort(num.begin(), num.end());
    num.erase(std::unique(num.begin(), num.end()), num.end());
    std::sort(idx + 1, idx + 2 * p + 1, [](int i, int j) {
        return x[i] != x[j] ? x[i] < x[j] : y[i] < y[j];
    });
    for (int i = 1; i <= 2 * p; i++) c[i] = 2 * n;
    ll ans = 2 * n;
    for (int i = 1; i <= 2 * p; i++) {
        int cur = idx[i];
        if (x[cur] > n || y[cur] > n) continue;
        dp[cur] = x[cur] + y[cur]; // 从(0,0)直接走过来
        int d = discretize(y[cur]);
        dp[cur] = std::min(dp[cur], query(d) + x[cur] + y[cur]);
        if (from[cur] != 0) { // 如果是某个跳板的右上端点
            dp[cur] = std::min(dp[cur], dp[from[cur]]);
        }
        ans = std::min(ans, n - x[cur] + n - y[cur] + dp[cur]);
        update(d, dp[cur] - x[cur] - y[cur]);
    }
    printf("%lld\n", ans);
    return 0;
}

posted @ 2024-06-10 08:31 RonChen 阅读(84) 评论(0) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

相关博文：

· 树上前缀和与差分

· 树的DFS序

· 树状数组：从基础到极致

· 树状数组专题

· 树状数组修改及查询操作

阅读排行：
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型，支持深度思考和联网搜索！
· 基于 Docker 搭建 FRP 内网穿透开源项目（很简单哒）
· ollama系列1：轻松3步本地部署deepseek，普通电脑可用
· 按钮权限的设计及实现
· 【杂谈】分布式事务——高大上的无用知识？

公告

昵称： RonChen
园龄： 8年9个月
粉丝： 5
关注： 0

+加关注

2025年3月

日

一

二

三

四

五

六

RonChen

树状数组

例题：P3374 【模板】树状数组 1

例题：P3368 【模板】树状数组 2

例题：P1908 逆序对

习题：P5459 [BJOI2016] 回转寿司

习题：P6186 [NOI Online #1 提高组] 冒泡排序

树状数组优化 DP

例题：P3431 [POI 2005] AUT-The Bus

习题：P6007 [USACO20JAN] Springboards G

公告

搜索

常用链接

合集

随笔档案

阅读排行榜

推荐排行榜

	x 二进制表示：0101...1000...0
	-x 的反码表示：1010...0111...1
	-x 的补码表示：1010...1000...0

	int query(int x) {
	int res = 0;
	while (x > 0) {
	res += c[x]; x -= lowbit(x); // 从大到小将需要的值求和
	}
	return res;
	}

	void add(int x, int y) {
	while (x <= n) {
	c[x] += y; x += lowbit(x); // 从小到大修改需要修改的位置
	}
	}

	#include <cstdio>
	typedef long long LL;
	const int MAXN = 5e5 + 5;
	LL a[MAXN];
	int n, m;
	int lowbit(int x) {
	return x & -x;
	}
	LL query(int x) {
	LL ret = 0;
	while (x > 0) {
	ret += a[x];
	x -= lowbit(x);
	}
	return ret;
	}
	void update(int x, LL d) {
	while (x <= n) {
	a[x] += d;
	x += lowbit(x);
	}
	}
	int main()
	{
	scanf("%d%d", &n, &m);
	for (int i = 1; i <= n; i++) {
	int x;
	scanf("%d", &x);
	update(i, x);
	}
	while (m--) {
	int op, x, y;
	scanf("%d%d%d", &op, &x, &y);
	if (op == 1) update(x, y);
	else printf("%lld\n", query(y) - query(x - 1));
	}
	return 0;
	}

	#include <cstdio>
	const int MAXN = 5e5 + 5;
	int a[MAXN], n;
	int lowbit(int x) {
	return x & -x;
	}
	int query(int x) {
	int ret = 0;
	while (x > 0) {
	ret += a[x];
	x -= lowbit(x);
	}
	return ret;
	}
	void update(int x, int d) {
	while (x <= n) {
	a[x] += d;
	x += lowbit(x);
	}
	}
	int main()
	{
	int m, pre = 0;
	scanf("%d%d", &n, &m);
	for (int i = 1; i <= n; i++) {
	int x;
	scanf("%d", &x);
	update(i, x - pre);
	pre = x;
	}
	while (m--) {
	int op;
	scanf("%d", &op);
	if (op == 1) {
	int x, y, k;
	scanf("%d%d%d", &x, &y, &k);
	update(x, k); update(y + 1, -k);
	} else {
	int x;
	scanf("%d", &x);
	printf("%d\n", query(x));
	}
	}
	return 0;
	}

	#include <cstdio>
	#include <vector>
	#include <algorithm>
	using std::lower_bound;
	using std::sort;
	using std::unique;
	using std::vector;
	typedef long long LL;
	const int N = 5e5 + 5;
	int n, a[N], bit[N], bound;
	vector<int> data;
	int discretization(int x) { // 求出x是第几小
	return lower_bound(data.begin(), data.end(), x) - data.begin() + 1;
	}
	int lowbit(int x) {
	return x & -x;
	}
	void add(int x) {
	while (x <= bound) {
	bit[x]++; x += lowbit(x);
	}
	}
	int query(int x) {
	int res = 0;
	while (x > 0) {
	res += bit[x]; x -= lowbit(x);
	}
	return res;
	}
	int main()
	{
	scanf("%d", &n);
	for (int i = 1; i <= n; i++) {
	scanf("%d", &a[i]); data.push_back(a[i]);
	}
	// 离散化的准备工作
	sort(data.begin(), data.end());
	data.erase(unique(data.begin(), data.end()), data.end());
	bound = data.size();
	LL ans = 0;
	for (int i = n; i >= 1; i--) {
	ans += query(discretization(a[i]) - 1);
	add(discretization(a[i]));
	}
	printf("%lld\n", ans);
	}

	#include <cstdio>
	#include <algorithm>
	using std::swap;
	using std::min;
	typedef long long LL;
	const int N = 2e5 + 5;
	int n, p[N], f[N];
	// 树状数组inv用于求一开始的f[i]
	// 树状数组cnt用于维护f[i]的个数的前缀和
	// 树状数组sum用于维护f[i]的前缀和
	LL sum[N], cnt[N], inv[N];
	int lowbit(int x) {
	return x & -x;
	}
	void update(LL bit[], int x, int delta) {
	while (x <= n) {
	bit[x] += delta; x += lowbit(x);
	}
	}
	LL query(LL bit[], int x) {
	LL res = 0;
	while (x > 0) {
	res += bit[x]; x -= lowbit(x);
	}
	return res;
	}
	int main()
	{
	int m; scanf("%d%d", &n, &m);
	for (int i = 1; i <= n; i++) {
	scanf("%d", &p[i]);
	f[p[i]] = query(inv, n) - query(inv, p[i]);
	if (f[p[i]] > 0) {
	update(sum, f[p[i]], f[p[i]]);
	update(cnt, f[p[i]], 1);
	}
	update(inv, p[i], 1);
	}
	while (m--) {
	int t, c; scanf("%d%d", &t, &c);
	if (t == 1) {
	int i = p[c] < p[c + 1] ? p[c] : p[c + 1];
	// 注意不要忘了判f[i]>0
	if (f[i] > 0) {
	update(sum, f[i], -f[i]);
	update(cnt, f[i], -1);
	}
	f[i] += p[c] < p[c + 1] ? 1 : -1;
	if (f[i] > 0) {
	update(sum, f[i], f[i]);
	update(cnt, f[i], 1);
	}
	swap(p[c], p[c + 1]);
	} else {
	c = min(c, n - 1); // 冒泡排序n-1轮过后足够完成排序
	LL ans = query(sum, n) - query(sum, c) - (query(cnt, n) - query(cnt, c)) * c;
	printf("%lld\n", ans);
	}
	}
	return 0;
	}