背包问题
背包类问题是动态规划的一类问题模型,这类模型应用广泛。背包类问题通常可以转化成以下模型:有若干个物品,每个物品有自己的重量和价值。选择物品放进一个容量有限的背包里,求出在容量不超过最大限度的情况下能拿到的最大总价值。
01 背包问题
背包类问题中最简单的是 01 背包问题:有 \(n\) 个物品,编号分别为 \(1 \sim n\),其中第 \(i\) 个物品的价值是 \(v_i\),重量是 \(w_i\)。有一个容量为 \(c\) 的背包,问选取哪些物品,可以使得在总重量不超过背包容量的情况下,拿到的物品的总价值最大。这里的每个物品都可以选择拿或不拿。因为每个物品只能用一次,我们用 \(0\) 表示不要这个物品,用 \(1\) 表示要这个物品,因此每个物品的决策就是 \(0\) 或者 \(1\)。这就是 01 背包这个名字的来源。
看到这个问题很多人的第一反应是使用贪心策略。对于每个物品,计算其性价比:用这个物品的价值除以其重量,得到一个比值。性价比越高,说明该物品越划算,应该尽量拿该物品。将所有物品按照性价比从高到低排序,只要当前背包还能装得下,就按照顺序一个一个地放进背包。
贪心策略对于大多数情况是比较有效的。不过很容易找到反例,例如,背包容量是 \(100\),\(3\) 个物品的重量分别是 \(51,50,50\),价值分别是 \(52,50,50\),可以看到,\(1\) 号物品性价比很高,优先拿 \(1\) 号物品。可是一旦选择了 \(1\) 号物品,背包容量就只剩下 \(49\),无法再拿 \(2\) 号或者 \(3\) 号物品。可是如果放弃 \(1\) 号物品,选择两个看起来不是很划算的 \(2\) 号和 \(3\) 号物品,总的背包容量刚好够用,这时候的总价值是 \(100\),比刚才的 \(52\) 要多。
所以可以看到,贪心策略无效,需要寻找一个动态规划的解决方案。首先划分阶段,那么应该一个一个物品地考虑,先考虑第一个物品时的决策,然后考虑新加入一个物品,决策有没有变化。而对于同一个物品,背包容量不同,最优结果也是不同的,所以背包容量也是状态的一部分。
定义 \(dp_{i,j}\) 表示只考虑前 \(i\) 个物品(并且正准备考虑第 \(i\) 个物品),在背包容量不超过 \(j\) 的情况下,能拿到的最大价值。对于当前物品,有两种决策方式,分别是这个物品拿或者不拿。如果拿这个物品,那么它会占用 \(w_i\) 的重量,留给前 \(i-1\) 个物品的容量就只剩下 \(j-w_i\) 了,在这个基础上我们能多拿到的价值是 \(v_i\)。如果不拿当前物品,相当于问题转化成前 \(i-1\) 个物品可使用的背包容量是 \(j\)。这两种决策下我们应该选一个最优的,也就是取最大值,所以状态转移方程是:\(dp_{i,j} = \max \{ dp_{i-1,j}, dp_{i-1,j-w_i} + v_i \}\)
例如假设有 \(3\) 个物品,背包容量是 \(4\),重量分别是 \(1,2,3\),价值分别是 \(2,3,1\)。考虑第 \(1\) 个物品,重量是 \(1\),价值是 \(2\)。计算 \(dp_{1,1}\) 的值,就是只考虑第 \(1\) 个物品,并且背包容量是 \(1\) 的时候,最大能取到的价值。如果不拿这个物品,该物品不占背包容量,相当于前 \(0\) 个物品,允许占用的背包容量是 \(1\),此时的最大价值是 \(dp_{0,1}\),显然结果是 \(0\)。如果拿这个物品,它自己占了一个单位空间,留给前 \(0\) 个物品的容量就是 \(0\),加上拿该物品获得的价值 \(2\),结果是 \(dp_{0,0}+2\)。对于这两种情况,选择价值最大的一种,所以 \(dp_{1,1} = max \{ dp_{0,1},dp_{0,0}+2 \} = 2\)。同理,\(dp_{1,2},dp_{1,3},dp_{1,4}\) 也都可以计算出结果为 \(2\)。这表示,当只有第 \(1\) 个物品,背包容量限制是 \(1 \sim 4\) 时,都可以拿到最大价值 \(2\),这与预期是相符的。
接下来考虑新引入第 \(2\) 个物品,它的重量是 \(2\),价值是 \(3\),先考虑 \(dp_{2,1}\) 的值,因为目前的背包容量是 \(1\),而第 \(2\) 个物品的重量是 \(2\),装不下,所以此处的决策只能是不要第 \(2\) 个物品,\(dp_{2,1}=dp_{1,1}=2\)。在计算 \(dp_{2,2}\) 时,因为容量够拿第 \(2\) 个物品,可以从拿或者不拿中选择价值最大的。如果拿,剩下的背包容量就只有 \(0\) 了,但是可以使拿到的价值加 \(3\),即 \(dp_{2,2}=\max \{ dp_{1,2},dp_{1,0}+3 \} = 3\),这个决策表明,当有 \(2\) 个物品,并且背包容量是 \(2\) 时,拿第 \(2\) 个物品更划算,可以得到 \(3\) 的价值。按照同样的计算方式可以依次得到 \(dp_{2,3}\) 和 \(dp_{2,4}\) 的值,结果都为 \(5\)。
考虑第 \(3\) 个物品后,用同样的方式递推,最终可以得到结果如下:
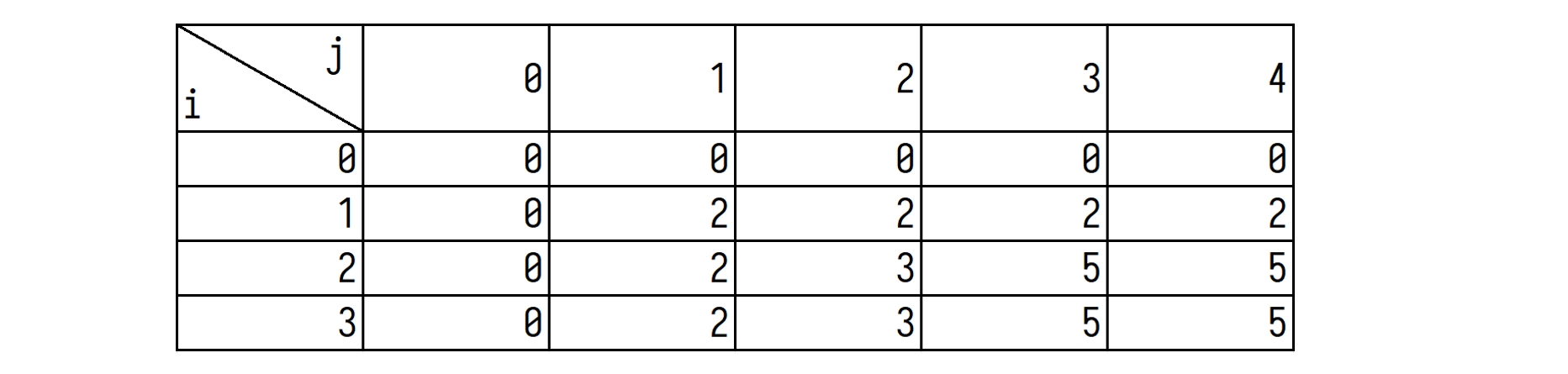
最终答案就是 \(dp_{3,4}\),含义是考虑前 \(3\) 个物品(也就是全部物品),背包容量为 \(4\) 时,最大总价值为 \(5\)。容易发现,最后两行结果一样。这其实说明第 \(3\) 个物品在决策时产生不了选它能提升价值的情况。
通过这样的方式,就完成了 01 背包问题的求解,时间复杂度为 \(O(nc)\)。
如果某个算法的时间复杂度是关于输入数据中绝对值最大的数值的多项式量级,则称该算法为伪多项式时间算法。由于输入数据中的具体数值可以取到输入数据规模的指数量级,因此伪多项式时间算法并不一定是真正的多项式时间算法。例如,01 背包问题的动态规划算法是一个伪多项式时间算法,而非多项式时间算法。
例题:P1048 [NOIP2005 普及组] 采药
本题是 01 背包问题的模板题,采药的总时间 \(T\) 就相当于背包容量,每一株草药就是一个物品,采药花费的时间相当于重量,草药的价值相当于物品的价值。
#include <cstdio>
#include <algorithm>
using std::max;
const int M = 105;
const int T = 1005;
int dp[M][T];
int main()
{
int t, m; scanf("%d%d", &t, &m);
for (int i = 1; i <= m; i++) { // 第i株草药
int tm, val; scanf("%d%d", &tm, &val); // 草药的采摘时间和价值
for (int j = 0; j <= t; j++) { // 背包容量
dp[i][j] = dp[i - 1][j]; // 第i株草药不选的决策必然能做
if (j >= tm) { // 背包容量足够才能考虑采摘
dp[i][j] = max(dp[i][j], dp[i - 1][j - tm] + val);
}
}
}
printf("%d\n", dp[m][t]);
return 0;
}
上面的代码中使用了二维数组,空间复杂度为 \(O(MT)\),能否优化到一维呢?
由于数组 dp 只有相邻两行之间有关系,可以滚动数组优化。
参考代码
#include <cstdio>
#include <algorithm>
using std::max;
const int M = 105;
const int T = 1005;
int dp[2][T], tm[M], val[M];
int main()
{
int t, m; scanf("%d%d", &t, &m);
for (int i = 1; i <= m; i++) scanf("%d%d", &tm[i], &val[i]);
for (int i = 1; i <= m; i++) {
int cur = i % 2, pre = 1 - cur;
for (int j = 0; j <= t; j++) {
dp[cur][j] = dp[pre][j];
if (j >= tm[i]) dp[cur][j] = max(dp[cur][j], dp[pre][j - tm[i]] + val[i]);
}
}
printf("%d\n", dp[m % 2][t]);
return 0;
}
更进一步,能否优化到一维?可以,但要注意枚举顺序。

根据状态转移方程,要计算 D 的值,需要用到第 \(i-1\) 行 E 和 C 两个位置的值。同理,计算 A 的值时需要用到 C 和 B 两个位置的值。在二维数组中,这些都可以正确执行。尝试压缩空间,将数组保留为一行。当计算完位置 D 的值以后,会覆盖掉原来位置 C 的值。
这时就产生了问题。当要计算位置 A 的值时,本来要用位置 C 的值,但是该值已被计算出来的位置 D 的值覆盖,拿不到想要的值,计算会发生错误。
所以需要将对 \(j\) 的循环逆序进行,先计算右边的列,再计算左边的列。从图中可以看到,如果在计算第 \(i\) 行的结果时先计算第 \(j\) 列位置 A 的值,然后把结果写到位置 B,即使覆盖掉第 \(i-1\) 列的值也没有关系,因为再往前的计算(例如计算 D 位置的值)不会再用到位置 B 的值。
这样压缩空间后,代码变得更为简洁:
#include <cstdio>
#include <algorithm>
using std::max;
const int M = 105;
const int T = 1005;
int dp[T], tm[M], val[M];
int main()
{
int t, m; scanf("%d%d", &t, &m);
for (int i = 1; i <= m; i++) scanf("%d%d", &tm[i], &val[i]);
for (int i = 1; i <= m; i++) {
for (int j = t; j >= tm[i]; j--) {
dp[j] = max(dp[j], dp[j - tm[i]] + val[i]);
}
}
printf("%d\n", dp[t]);
return 0;
}
可以发现,最开始的代码里有一个 if 判断,而最终空间压缩后的代码中没有。优化前的代码中的 if 判断,是为了判断当前的消耗时间是否足够采摘第 \(i\) 株草药,如果能装下,就考虑采或不采两种决策。如果时间不够采,直接让 \(dp_{i,j}\) 等于上一行的结果,也就是 \(dp_{i-1,j}\)。而在优化后的程序中,倒着循环到 \(tm_i\),这些都是时间足够采的情况。而小于 \(tm_i\) 的部分,就直接不循环了,如此一来,这些位置的值也都不会改变,都会保留上一行的结果,正好是想要的效果。
例题:P1049 [NOIP2001 普及组] 装箱问题
首先,容易看出题目中的每个物品就是背包类问题中的“物品”,每个物品只能选一次,所以此题属于 01 背包问题。不过题目中并没有给出物品的价值和重量,只是给了物品的体积。需要找到对应物品价值和重量的定义方式,来吧问题转化成标准的背包问题。
题中问如何能让剩余空间最小,转化一下,其实就是问如何能尽量装最多的物品。求出物品的最大占用空间,用总空间减去最大占用空间,就能得到最小剩余空间了。所以,优化的目标就是如何利用最多的空间,可以看出,空间其实就是价值,想让价值尽可能大。同样,因为总体积不能超过 \(V\),每个物品也有自己的体积,可以看出,物品的重量其实就是它的体积。因此,物品的重量和价值是一样的,都是它的体积。
定义 \(dp_{i,j}\) 表示用前 \(i\) 个物品,背包容量为 \(j\) 时,能取得的最大收益(占用空间)。状态转移方程为:\(dp_{i,j} = \max \{ dp_{i-1,j}, dp_{i-1,j-vol_i} + vol_i \}\)。
参考代码
#include <cstdio>
#include <algorithm>
using std::max;
const int N = 35;
const int V = 20005;
int dp[N][V], vol[N];
int main()
{
int v, n; scanf("%d%d", &v, &n);
for (int i = 1; i <= n; i++) scanf("%d", &vol[i]);
for (int i = 1; i <= n; i++) {
for (int j = 0; j <= v; j++) {
dp[i][j] = dp[i - 1][j];
if (j >= vol[i]) dp[i][j] = max(dp[i][j], dp[i - 1][j - vol[i]] + vol[i]);
}
}
printf("%d\n", v - dp[n][v]);
return 0;
}
同样,也可以压缩到一维数组。
参考代码
#include <cstdio>
#include <algorithm>
using std::max;
const int N = 35;
const int V = 20005;
int dp[V], vol[N];
int main()
{
int v, n; scanf("%d%d", &v, &n);
for (int i = 1; i <= n; i++) scanf("%d", &vol[i]);
for (int i = 1; i <= n; i++) {
for (int j = v; j >= vol[i]; j--) {
dp[j] = max(dp[j], dp[j - vol[i]] + vol[i]);
}
}
printf("%d\n", v - dp[v]);
return 0;
}
习题:AT_dp_d Knapsack 1
解题思路
模板背包问题。
参考代码
#include <cstdio>
#include <algorithm>
using ll = long long;
using std::max;
const int W = 100005;
ll dp[W];
int main()
{
int n, maxw; scanf("%d%d", &n, &maxw);
for (int i = 1; i <= n; i++) {
int w, v; scanf("%d%d", &w, &v);
for (int j = maxw; j >= w; j--)
dp[j] = max(dp[j], dp[j - w] + v);
}
printf("%lld\n", dp[maxw]);
return 0;
}
例题:P1060 [NOIP2006 普及组] 开心的金明
此题是标准的 01 背包模板题。价格与重要度的乘积是该物品的价值,所以在读入重要度 \(w_i\) 时,不妨直接将 \(w_i\) 更新为 \(w_i \times v_i\)。令 \(dp_{i,j}\) 表示考虑前 \(i\) 个物品,钱数为 \(j\) 时,可以获得的最大价值。如果不选取第 \(i\) 个物品或钱不够时(\(j < v_i\)),\(dp_{i,j} = dp_{i-1,j}\);如果选取第 \(i\) 个物品,付出 \(v_i\) 元钱,收获 \(w_i\) 的价值,即 \(dp_{i,j} = dp_{i-1,j-v_i}+w_i\)。状态转移方程是对以上两种情况取最大值。
参考代码
#include <cstdio>
#include <algorithm>
using std::max;
const int M = 30;
const int N = 30005;
int v[M], w[M], dp[M][N];
int main()
{
int n, m; scanf("%d%d", &n, &m);
for (int i = 1; i <= m; i++) {
scanf("%d%d", &v[i], &w[i]);
w[i] *= v[i];
}
for (int i = 1; i <= m; i++) { // 第i个物品
for (int j = 0; j <= n; j++) { // 钱数
dp[i][j] = dp[i - 1][j]; // 不要这个物品或钱不够
if (j >= v[i]) dp[i][j] = max(dp[i][j], dp[i - 1][j - v[i]] + w[i]); // 钱够
}
}
printf("%d\n", dp[m][n]);
return 0;
}
同样,也可以压缩到一维数组。
参考代码
#include <cstdio>
#include <algorithm>
using std::max;
const int M = 30;
const int N = 30005;
int v[M], w[M], dp[N];
int main()
{
int n, m; scanf("%d%d", &n, &m);
for (int i = 1; i <= m; i++) {
scanf("%d%d", &v[i], &w[i]);
w[i] *= v[i];
}
for (int i = 1; i <= m; i++) {
for (int j = n; j >= v[i]; j--) {
dp[j] = max(dp[j], dp[j - v[i]] + w[i]);
}
}
printf("%d\n", dp[n]);
return 0;
}
例题:P1164 小A点菜
由于“每种菜品只有一份”,所以本题是 01 背包问题。与前面不同的是,这里要求的不是最大价值而是方案数。
在 01 背包问题中,我们是针对顶 \(i\) 个物品要或者不要的情况,求一个最大价值。而本题要计算方案数,如果不要第 \(i\) 个物品,则前 \(i-1\) 个物品有多少种方案,现在都可以纳入前 \(i\) 个物品的方案。如果要第 \(i\) 个物品,那么前 \(i-1\) 个物品在背包容量减少的情况下的所有情况,也都可以转移过来。所以总方案数是第 \(i\) 个物品要和不要两种情况的和。
注意,当容量为 \(0\) 时,不选择任何一种菜品,也是一种方案,需要初始化。
参考代码
#include <cstdio>
const int N = 105;
const int M = 10005;
int dp[N][M];
int main()
{
int n, m; scanf("%d%d", &n, &m);
dp[0][0] = 1;
for (int i = 1; i <= n; i++) {
int a; scanf("%d", &a);
for (int j = 0; j <= m; j++) {
dp[i][j] = dp[i - 1][j];
if (j >= a) dp[i][j] += dp[i - 1][j - a];
}
}
printf("%d\n", dp[n][m]);
return 0;
}
例题:P1510 精卫填海
根据题意,剩下的 \(n\) 块木石每块最多可以用一次,也可以选择不用,所以,这是一个 01 背包问题。定义 \(dp_{i,j}\) 表示体力为 \(j\) 时,只考虑前 \(i\) 块木石的情况下所获得的最大体积。状态转移方程为:\(dp_{i,j} = dp_{i-1,j}, dp_{i-1, j - w_i} + val_i\)。式中,\(w_i\) 表示将第 \(i\) 块木石衔到东海耗费的体力,\(val_i\) 表示这块木石的体积。
此题想要尽可能留更多的体力,也就是尽可能少花费体力,相当于希望 \(dp_{i,j} \ge v\) 的情况下 \(j\) 尽可能小,这样剩余的最大体力为 \(c-j\)。如果不存在大于等于 \(v\) 的状态,输出 Impossible。
此题同样可以压缩到一维数组实现。
参考代码
#include <cstdio>
#include <algorithm>
using std::max;
const int C = 1e4 + 5;
int dp[C];
int main()
{
int v, n, c; scanf("%d%d%d", &v, &n, &c);
int ans = -1;
for (int i = 1; i <= n; i++) {
int val, w; scanf("%d%d", &val, &w);
for (int j = c; j >= w; j--) { // 枚举体力j
dp[j] = max(dp[j], dp[j - w] + val);
if (dp[j] >= v) ans = max(ans, c - j);
}
}
if (ans == -1) printf("Impossible\n");
else printf("%d\n", ans);
return 0;
}
例题:P1507 NASA的食物计划
之前背包问题的费用都是一维的,即每个物品有自己的重量。这里每个物品有自己的重量和体积,背包的限制也是二维的,总重量不能超过限制,总体积也不能超过限制,问如何选取物品能使得总价值最大,这就是二维费用背包问题。
既然费用多了一维,那么状态也可以增加一维。设 \(dp_{i,u,v}\) 表示前 \(i\) 件物品两种费用限制分别为 \(u\) 和 \(v\) 时可获得的最大价值,用 \(c_i\) 和 \(d_i\) 表示每种物品的两种费用,用 \(w_i\) 表示该物品的价值。状态转移方程就是:\(dp_{i,u,v} = \max \{ dp_{i-1,u,v}, dp_{i-1,u-c_i,v-d_i} + w_i \}\)。
类似地,可以优化空间复杂度,降一维空间到二维数组。
参考代码
#include <cstdio>
#include <algorithm>
using std::max;
const int H = 405;
int dp[H][H];
int main()
{
int maxh, maxt, n; scanf("%d%d%d", &maxh, &maxt, &n);
for (int i = 1; i <= n; i++) {
int h, t, cal; scanf("%d%d%d", &h, &t, &cal);
for (int j = maxh; j >= h; j--) {
for (int k = maxt; k >= t; k--) {
dp[j][k] = max(dp[j][k], dp[j - h][k - t] + cal);
}
}
}
printf("%d\n", dp[maxh][maxt]);
return 0;
}
习题:P1802 5 倍经验日
题目分析
本题要求在拥有 \(x\) 个药剂的限制下,通过挑战 \(n\) 个对手来获取最高总经验。对于每个对手,有两种选择:
- 挑战并获胜:消耗 \(use\) 个药剂,获得 \(win\) 点经验。
- 挑战并失败:不消耗药剂,获得 \(lose\) 点经验。
目标是求出最大总经验,并输出其 5 倍。
解题思路
这个问题可以转化为一个经典的 0/1 背包问题。
可以换一个角度思考:无论如何,至少可以获得所有战斗失败的经验。决策点在于,要不要花费额外的药剂,将某场战斗的“失败”结果升级为“胜利”结果,从而获得更高的经验。
- 基础经验:假设和所有人都战斗并失败,不需要消耗任何药剂,获得的总经验是所有 \(lose\) 之和。
- 升级选项:对于第 \(i\) 个人,可以选择花费 \(use_i\) 的药剂,将结果从“失败”变为“胜利”。这个“升级”操作带来的额外经验收益是 \(win_i - lose_i\)。
这样,问题就转换成了一个标准的 0/1 背包问题:
- 背包容量:总药剂数量 \(x\)
- 物品:共有 \(n\) 个物品,每个物品对应一个“升级”选项
- 物品 \(i\) 的重量:“升级”需要消耗的药剂数量 \(use_i\)
- 物品 \(i\) 的价值:“升级”带来的额外经验收益 \(win_i - lose_i\)
需要求解:在不超过背包总容量 \(x\) 的前提下,选择若干物品(“升级”选项),使得总价值(总额外经验)最大。
定义一个 DP 数组,\(dp_j\) 表示花费 \(j\) 个药剂所能获得的最大额外经验。
遍历每一个人(即每一个物品),对于每一个人,用 0/1 背包的标准方式更新 \(dp\) 数组,状态转移方程:\(dp_j \leftarrow \max (dp_j, dp_{j - use_i} + (win_i - lose_i))\)。
这个方程的含义是对于当前拥有 \(j\) 个药剂的情况,可以选择:
- 不升级第 \(i\) 个人:那么最大额外经验依然是 \(dp_j\)(即不花费 \(use_i\) 药剂在第 \(i\) 个人身上)。
- 升级第 \(i\) 个人:这需要 \(use_i\) 的药剂,那么就需要用 \(j - use_i\) 的药剂去获取之前的最大额外经验 \(dp_{j - use_i}\),然后再加上升级第 \(i\) 个人获得的额外经验 \(win_i - lose_i\)。
在这两种选择中取最大值,如果为了优化空间使用一维数组,需要逆序遍历药剂数量 \(j\)(从 \(x\) 到 \(use_i\))。
通过上述 DP 计算,\(dp_x\) 就是使用 \(x\) 个药剂能获得的最大额外经验。
最终的总经验应该是基础经验加上最大额外经验。
最后,根据题目要求,输出这个值的 5 倍即可。
参考代码
#include <cstdio>
#include <algorithm>
using namespace std;
const int W = 1e3 + 5;
// dp[j] 定义为:使用 j 个药剂能获得的 "最大额外经验"。
// 这是标准的 0/1 背包解法,将问题转化为:
// 背包容量为 x,每个对手是一个物品,重量是 use[i],价值是 win[i] - lose[i]。
int dp[W];
int main()
{
int n, x; // n: 对手数量, x: 药剂数量
scanf("%d%d", &n, &x);
// sum 用于累计所有 lose[i] 的和,作为保底的基础经验。
int sum = 0;
// 遍历 n 个对手(物品)
for (int i = 1; i <= n; i++) {
int lose, win, use; // 失败经验, 胜利经验, 胜利所需药剂
scanf("%d%d%d", &lose, &win, &use);
sum += lose; // 累加基础经验
// 0/1 背包核心代码:逆序遍历背包容量
for (int j = x; j >= use; j--) {
// 状态转移方程
// dp[j]:不选择战胜当前对手,额外经验不变。
// dp[j - use] + win - lose:选择战胜当前对手,
// 用 j-use 的容量获取之前的最大额外经验,并加上本次胜利带来的额外经验。
dp[j] = max(dp[j], dp[j - use] + win - lose);
}
}
// 最大总经验 = 基础经验 (sum) + x个药剂换来的最大额外经验 (dp[x])
// 乘以 5ll (long long 类型的5) 防止溢出
printf("%lld\n", 5ll * (sum + dp[x]));
return 0;
}
例题:P1504 积木城堡
\(n\) 座城堡是相互独立的,可以单独考虑。
对于当前正在考虑的城堡,每块积木只能选去还是一次或不选,所以此题为 01 背包问题。每块积木是否选取会影响城堡的高度,用 \(dp_{i,j}\) 表示通过前 \(i\) 块积木能否达到高度 \(j\)。因为关心的是能否达到,所以这个数组可以是布尔数组,\(dp_{i,j}=false\) 代表不能达到高度 \(j\);\(dp_{i,j}=true\) 表示能达到高度 \(j\)。
用 len 表示第 \(i\) 块积木的高度,则状态转移方程相当于:if (dp[i][j - len]) dp[i][j] = true;,即如果使用这块积木之前的高度(当前高度减这块积木高度)可以达到,那么当前高度也可以达到。这样使用 01 背包问题的求解思路即可求出当前城堡能达到的所有高度。
现在题目要求的是哪个最大高度是所有城堡都能达到的。可以统计某个高度在这 \(n\) 个城堡下达到的次数,用 \(cnt_j\) 表示高度 \(j\) 有多少个城可以达到这个高度。这样在处理完每座城堡后,如果某个高度可以达到,对应计数加一即可。\(n\) 座城堡计算完成后,如果有 \(cnt_j = n\),说明每个城堡都能实现这个高度,找这样的最大的 \(j\) 即可。
参考代码
#include <cstdio>
#include <algorithm>
using std::max;
const int N = 105;
bool dp[N * N];
int cnt[N * N];
int main()
{
int n; scanf("%d", &n);
int maxsum = 0;
for (int i = 1; i <= n; i++) { // n座城堡
int sum = 0;
dp[0] = true; // 一开始只有高度为0可以达到
while (true) { // 循环读入积木信息
int len; scanf("%d", &len);
if (len == -1) break;
sum += len;
for (int j = sum; j >= len; j--) {
dp[j] |= dp[j - len]; // 如果高度j-len可以到达,那么高度j也能到达
}
}
for (int j = sum; j >= 0; j--)
if (dp[j]) {
cnt[j]++; // 可以达到该高度的城堡数量+1
dp[j] = false; // 清空dp数组以备下一个城堡计算时使用
}
maxsum = max(maxsum, sum);
}
int ans = 0;
for (int i = maxsum; i >= 0; i--) { // 找到n个城堡都能达成的最大高度
if (cnt[i] == n) {
ans = i; break;
}
}
printf("%d\n", ans);
return 0;
}
习题:AT_dp_e Knapsack 2
解题思路
本题和普通的背包问题描述是一样的,只有数据范围不一样。改动数据范围后,普通的时间复杂度为 \(O(nW)\) 的背包做法无法通过。
注意到价值的范围比较小,所以可以考虑把每个物品的价值与重量互换。相当于求某价值下最少需要的背包容量。
参考代码
#include <cstdio>
#include <algorithm>
using ll = long long;
using std::min;
const int V = 100005;
const ll INF = 1e18;
ll dp[V];
int main()
{
int n, maxw;
scanf("%d%d", &n, &maxw);
int sumv = 0;
for (int i = 1; i <= n; i++) {
int w, v; scanf("%d%d", &w, &v);
for (int j = sumv + 1; j <= sumv + v; j++) dp[j] = INF;
sumv += v;
for (int j = sumv; j >= v; j--) {
dp[j] = min(dp[j], dp[j - v] + w);
}
}
for (int i = sumv; i >= 0; i--)
if (dp[i] <= maxw) {
printf("%d\n", i); break;
}
return 0;
}
习题:P1455 搭配购买
题目分析
本题的核心在于“搭配购买”的规则:如果物品 A 和 B 有搭配关系,那么购买 A 就必须购买 B,反之亦然。这个关系具有传递性:如果 A 和 B 必须一起买,B 和 C 必须一起买,那么购买 A、B、C 中任意一个,就必须把这三个都买下。
这意味着,所有通过搭配关系连接起来的物品形成了一个不可分割的整体。不能只买这个整体中的一部分,要么全部买下,要么整个不买。
因此,解题思路分为两大步:
- 物品分组:找出所有这样的“物品组”,并计算每个组的总价格和总价值。
- 选择决策:将每个“物品组”看作一个全新的、独立的大物品,然后在这个基础上进行选择,以在有限的预算内获得最大价值。
解题思路
并查集是处理这类“连通”和“分组”问题的绝佳工具。
- 将 \(n\) 朵云看作 \(n\) 个独立的节点。
- 遍历 \(m\) 个搭配关系 \((u,v)\),如果 \(u\) 和 \(v\) 尚未在同一个集合中,就将它们合并。
- 在合并两个集合的同时,还需要将它们的总价格和总价值也合并。具体来说,如果将 \(v\) 所在的集合合并到 \(u\) 所在的集合,就将 \(v\) 集合的总价格和总价值累加到 \(u\) 集合的根节点上。
完成所有合并操作后,每个集合的根节点就代表一个完整的“物品组”,并且该根节点上存储了整个组的总价格和总价值。
经过上面的处理,原问题就转化成了一个标准的 0/1 背包问题。
- 背包容量:总钱数 \(w\)
- 物品:每一个由并查集构成的“物品组”
- 每个物品的重量:对应“物品组”的总价格
- 每个物品的价值:对应“物品组”的总价值
目标是从这些“物品组”中挑选若干个,放入背包,使得总重量不超过背包容量,且总价值最大。
可以定义一个 DP 数组,\(dp_j\) 表示花费 \(j\) 元钱能获得的最大价值。
遍历每一个“物品组”,然后用 0/1 背包的标准方式更新 \(dp\) 数组,状态转移方程:\(dp_j \leftarrow \max (dp_j, dp_{j - \text{group_cost}} + \text{group_value})\),其中 \(\text{group_cost}\) 和 \(\text{group_value}\) 分别是一个物品组的总价格和总价值。
最终,\(dp_w\) 就是能获得的最大价值。
参考代码
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 10005;
// c, d: 存储单个云朵的初始价格和价值
// fa: 并查集的父节点数组
// cost, value: 存储每个合并后的大物品(物品组)的总价格和总价值
// dp: 0/1背包的DP数组
int c[N], d[N], fa[N], cost[N], value[N], dp[N];
// 并查集的查询函数(带路径压缩)
// 找到 x 所在集合的根节点
int query(int x) {
return x == fa[x] ? x : fa[x] = query(fa[x]);
}
int main()
{
int n, m, w; // n:云朵数, m:搭配数, w:总钱数
scanf("%d%d%d", &n, &m, &w);
for (int i = 1; i <= n; i++) scanf("%d%d", &c[i], &d[i]);
// 1. 并查集初始化:每个云朵自成一个集合
for (int i = 1; i <= n; i++) fa[i] = i;
// 2. 处理搭配关系,合并集合
while (m--) {
int u, v; scanf("%d%d", &u, &v);
int fu = query(u); // u的根节点
int fv = query(v); // v的根节点
if (fu != fv) { // 如果不在同一个集合,则合并
// 将 fv 集合的成本和价值累加到 fu 集合的根节点上
c[fu] += c[fv];
d[fu] += d[fv];
// 合并集合
fa[fv] = fu;
}
}
// 3. 提取物品组,准备进行背包计算
int cnt = 0; // 记录物品组的数量
for (int i = 1; i <= n; i++)
// 如果一个节点是其所在集合的根节点,则它代表一个完整的物品组
if (query(i) == i) {
cnt++;
cost[cnt] = c[i]; // 第 cnt 个物品组的总价格
value[cnt] = d[i]; // 第 cnt 个物品组的总价值
}
// 4. 0/1 背包求解
// 遍历 cnt 个物品组
for (int i = 1; i <= cnt; i++)
// 逆序遍历背包容量
for (int j = w; j >= cost[i]; j--)
// 状态转移方程
dp[j] = max(dp[j], dp[j - cost[i]] + value[i]);
// dp[w] 即为预算为 w 时能获得的最大价值
printf("%d\n", dp[w]);
return 0;
}
习题:CF1954D Colored Balls
解题思路
考虑分组数量的消耗,每一组是最多取 \(2\) 个不同颜色的球。所以假如从全集中取了一部分球出来,其中某种颜色的球超过了一半,则分组数量就是这个颜色的球数,如果没有一种颜色的球的数量过半,则分组数量是 \(\lceil \frac{球的总数}{2} \rceil\)。
所以按球的数量排序,假设当前枚举的第 \(i\) 种球的数量是最多的,则前面的 \(i-1\) 种球构成的总数可能会超过第 \(i\) 种球的数量,也可能不超过,这两种情况需要的分组数已经在上一段中讨论了。我们还需要知道从前 \(i-1\) 种球选子集后形成的球的各种总数的方案数,这是一个 01 背包方案数问题。
参考代码
#include <cstdio>
#include <algorithm>
using std::sort;
typedef long long LL;
const int N = 5005;
const int MOD = 998244353;
int a[N], dp[N][N];
int main()
{
int n; scanf("%d", &n);
for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
sort(a + 1, a + n + 1);
dp[0][0] = 1;
int ans = 0;
for (int i = 1; i <= n; i++) {
for (int j = 0; j <= 5000; j++) {
if (dp[i - 1][j] == 0) continue;
if (j <= a[i]) {
int add = 1ll * dp[i - 1][j] * a[i] % MOD;
ans = (ans + add) % MOD;
} else {
int add = 1ll * dp[i - 1][j] * ((a[i] + j + 1) / 2) % MOD;
ans = (ans + add) % MOD;
}
}
for (int j = 0; j <= 5000; j++) {
dp[i][j] = dp[i - 1][j];
if (j >= a[i]) dp[i][j] = (dp[i][j] + dp[i - 1][j - a[i]]) % MOD;
}
}
printf("%d\n", ans);
return 0;
}
习题:P1417 烹调方案
问题分析
本题要求在总时间 \(T\) 内,选择一部分食材进行烹饪,以最大化所有完成菜品的总美味度。
每个食材 \(i\) 有三个属性:
- \(a_i\):基础美味度
- \(b_i\):美味度随时间的衰减率
- \(c_i\):烹饪所需时间
关键在于,一份菜的最终美味度取决于它的完成时刻 \(t\),计算公式为 \(a_i - t \times b_i\)。这意味着,越晚完成的菜,其美味度就越低。
这看起来像一个背包问题,总时间 \(T\) 是背包容量,\(c_i\) 是物品体积。但物品的“价值”(美味度)不是固定的,它依赖于放入背包的“顺序”。
核心思路
这是一个典型的排序贪心 + 动态规划问题。
首先,需要确定一个最优的烹饪顺序。如果已经决定要烹饪某个固定的食材集合,应该按照什么顺序来烹饪它们才能使得总美味度最高?
可以使用邻项交换法来证明,假设在烹饪序列中,有两个相邻的食材 \(i\) 和 \(j\),比较先做 \(i\) 后做 \(j\) 与先做 \(j\) 后做 \(i\) 的优劣。
假设在处理 \(i\) 和 \(j\) 之前,已经花费了时间 \(t_0\)。
- 顺序 \(i \rightarrow j\)
- \(i\) 的完成时刻是 \(t_0 + c_i\),美味度为 \(a_i - (t_0 + c_i) \times b_i\)。
- \(j\) 的完成时刻是 \(t_0 + c_i + c_j\),美味度为 \(a_j - (t_0 + c_i + c_j) \times b_j\)。
- 两者美味度之和为:\(a_i + a_j - t_0 \times (b_i + b_j) - c_i \times b_i - (c_i + c_j) \times b_j\)。
- 顺序 \(j \rightarrow i\)
- \(j\) 的完成时刻是 \(t_0 + c_j\),美味度为 \(a_j - (t_0 + c_j) \times b_j\)。
- \(i\) 的完成时刻是 \(t_0 + c_j + c_i\),美味度为 \(a_i - (t_0 + c_j + c_i) \times b_i\)。
- 两者美味度之和为:\(a_j + a_i - t_0 \times (b_j + b_i) - c_j \times b_j - (c_j + c_i) \times b_i\)。
为了让总美味度更高,假设顺序 \(i \rightarrow j\) 优于 \(j \rightarrow i\)。比较这两个和,去掉公共项 \(a_i, \ a_j, \ -t_0 \times (b_i + b_j)\),得到 \(-c_i \times b_i - (c_i + c_j) \times b_j \gt -c_j \times b_j - (c_j + c_i) \times b_i\),去掉公共项 \(-c_i \times b_i\) 和 \(-c_j \times b_j\),得到 \(-c_i \times b_j \gt -c_j \times b_i\),两边同乘 \(-1\),不等号反向,得到 \(c_i \times b_j \lt c_j \times b_i\)。
这个不等式意味着当 \(c_i \times b_j \lt c_j \times b_i\) 成立时,食材 \(i\) 应该排在食材 \(j\) 前面。这个排序规则可以进一步化为不等式两边分别是 \(\dfrac{c_i}{b_i}\) 和 \(\dfrac{c_j}{b_j}\),具有传递性,因此可以对所有食材进行全局排序。
在确定了最优烹饪顺序后,问题就转化为一个经典的 0/1 背包问题:依次考虑每一个排好序的食材,决定是“做”还是“不做”。
定义 \(dp_j\) 表示花费恰好为 \(j\) 的总时间,所能获得的最大总美味度。
按照排好的顺序遍历所有食材 \(i\),对于每个食材,如果决定烹饪它,并且烹饪完成后总耗时为 \(j\):
- 那么在烹饪 \(i\) 之前,已耗时 \(j - c_i\)
- 之前那些菜品(在 \(j - c_i\) 时间内完成)能提供的最大美味度是 \(dp_{j - c_i}\)
- 食材 \(i\) 是在最后完成的,其完成时刻就是当前的总耗时 \(j\),所以它自身的美味度是 \(a_i - j \times b_i\)
因此,状态转移方程为 \(dp_j \leftarrow \max (dp_j, \ dp_{j - c_i} + a_i - j \times b_i)\),其中前一项 \(dp_j\) 代表不烹饪食材 \(i\) 的情况。
由于美味度会随着时间衰减,所以花费的时间越长,总美味度不一定越高,最优解可能出现在总耗时小于 \(T\) 的某个时刻。
因此,最终的答案不是 \(dp_T\),而是 \(dp\) 数组中的最大值,即 \(\max(dp_j)\) 对于所有的 \(0 \le j \le T\)。
参考代码
#include <cstdio>
#include <algorithm>
using namespace std;
// 使用 long long 来防止计算过程中出现整数溢出
typedef long long LL;
const int MAXN = 55; // 最大食材数量
const int MAXM = 100005; // 最大总时间
// 定义食材结构体
struct Thing {
LL a, b; // a: 基础美味度, b: 衰减率
int c; // c: 烹饪时间
// 重载小于号运算符,用于自定义排序
// 排序规则推导:对于相邻的两个物品i和j,若先做i再做j更优,
// 则满足 c_i * b_j < c_j * b_i。
// 这里 a < b 的含义是 a 的优先级低于 b,即 b 应该排在 a 前面。
// 所以当 other.b * c < b * other.c (即 b_j*c_i < b_i*c_j) 时,
// this(i) 的优先级更低,应该排在 other(j) 后面,符合 sort 的升序逻辑。
bool operator<(const Thing& other) const {
return other.b * c < b * other.c;
}
};
Thing a[MAXN]; // 存储所有食材
LL dp[MAXM]; // DP数组, dp[j] 表示恰好花费 j 时间能获得的最大美味度
int main()
{
int t, n; // t: 总时间, n: 食材数量
scanf("%d%d", &t, &n);
// 读取食材数据
for (int i = 0; i < n; i++) scanf("%lld", &a[i].a);
for (int i = 0; i < n; i++) scanf("%lld", &a[i].b);
for (int i = 0; i < n; i++) scanf("%d", &a[i].c);
// 根据推导出的贪心策略对食材进行排序
sort(a, a + n);
// 0/1 背包过程
// 外层循环:按排好的最优顺序遍历每个食材
for (int i = 0; i < n; i++) {
// 内层循环:遍历背包容量(时间),压维必须倒序遍历以保证0/1背包性质
for (int j = t; j >= a[i].c; j--) {
// 状态转移方程
// dp[j] 的选择:
// 1. 不做食材i,保持 dp[j] 不变
// 2. 做食材i,则总美味度 = (做完前i-1个物品且总耗时为j-c[i]时的美味度) + (物品i自身的美味度)
// 物品i在时刻j完成,其美味度为 a[i].a - j * a[i].b
dp[j] = max(dp[j], dp[j - a[i].c] + a[i].a - j * a[i].b);
}
}
// 寻找最终答案
// 由于美味度会随时间衰减,最优解不一定恰好用完时间t
// 因此需要遍历所有可能的时间点,找到最大值
LL ans = 0;
for (int i = 0; i <= t; i++) {
ans = max(ans, dp[i]);
}
printf("%lld\n", ans);
return 0;
}
习题:P1441 砝码称重
解题思路
这个问题可以清晰地分解为两个子问题:
- 组合枚举:从 \(n\) 个砝码中选择 \(m\) 个去掉,需要遍历所有可能的选择方案。
- 称重计数:对于每一种选择方案(即剩下的 \(n-m\) 个砝码),需要计算它们能组合出多少种不同的重量。
最终的答案就是所有组合方案中,能够称出最多不同重量的那一个方案的数量。
由于 \(n\) 和 \(m\) 的数据范围很小(特别是 \(m\)),组合数 \(C_n^m\) 不会很大(例如,\(C_{20}^4=4845\)),这表明暴力枚举所有“去掉 \(m\) 个砝码”的组合是完全可行的。
对于第二个问题“称重计数”,这是一个经典的 0/1 背包问题 的变体。给定一些物品,每个物品只能选或不选,问能凑出的所有可能的总重量有哪些。
这个 DP 过程还可以用 bitset 优化,bitset 可以看作一个布尔数组,但相比之下其位运算速度更快。
参考代码
#include <cstdio>
#include <vector>
#include <algorithm>
#include <bitset>
using namespace std;
// 全局变量
int n, m;
vector<int> weights; // 存储所有n个砝码的重量
int max_reachable_count = 0; // 存储所有组合中,可称出重量数的最大值
// 根据数据规模,最大可能称出的总重量为 n * max_weight = 20 * 100 = 2000
const int MAX_SUM = 2001;
// 功能:对给定的砝码组合,计算可以称出的不同重量数
// 参数:current_selection - 一个包含 n-m 个砝码的 vector
void calculate_sums(const vector<int>& current_selection) {
if (current_selection.empty()) {
return;
}
// 使用 bitset 优化 0/1 背包问题
// reachable[j] = 1 表示重量 j 是可以被称出的
bitset<MAX_SUM> reachable;
reachable[0] = 1; // 重量0总是可达的(不放任何砝码)
// 遍历当前组合中的每一个砝码
for (int w : current_selection) {
// 关键步骤:dp |= (dp << w)
// 这行代码等价于一个 0/1 背包的内层循环:
// for(int j = MAX_SUM - 1; j >= w; --j) {
// reachable[j] = reachable[j] | reachable[j - w];
// }
// 其含义是:如果重量 j-w 是可达的,那么在放上砝码 w 后,重量 j 也变得可达。
// bitset 的位运算使得这个过程非常高效。
reachable |= (reachable << w);
}
// reachable.count() 返回 bitset 中为 1 的位数,即可以称出的总重量数(包括0)
// 题目要求不包括0,所以结果要减1
int current_count = reachable.count() - 1;
// 更新全局最大值
max_reachable_count = max(max_reachable_count, current_count);
}
// 功能:使用 DFS 来生成所有“保留 n-m 个砝码”的组合
// 参数:index - 当前正在考虑 weights 数组中的第 index 个砝码
// 参数:current_selection - 当前已经选入组合的砝码
void find_combinations(int index, vector<int>& current_selection) {
// 剪枝优化:如果剩下的所有砝码都选上,也不足以凑够 n-m 个,则当前分支无解
if (current_selection.size() + (n - index) < n - m) {
return;
}
// 递归终止条件:已经选了 n-m 个砝码,找到了一个完整的组合
if (current_selection.size() == n - m) {
calculate_sums(current_selection); // 对这个组合计算可称重数量
return;
}
// 递归终止条件:已经考察完所有砝码,但仍未选够 n-m 个
if (index == n) {
return;
}
// --- 递归分支 ---
// 分支1: 选择当前的砝码 weights[index]
current_selection.push_back(weights[index]);
find_combinations(index + 1, current_selection);
current_selection.pop_back(); // 回溯,撤销选择,为分支2做准备
// 分支2: 不选择当前的砝码 weights[index] (即丢弃它)
// 只有当已丢弃的砝码数小于 m 时,才能继续丢弃当前的砝码
// 已丢弃数 = 当前已考察的砝码数 - 当前已选择的砝码数 = index - current_selection.size()
if ((index - current_selection.size()) < m) {
find_combinations(index + 1, current_selection);
}
}
int main() {
scanf("%d%d", &n, &m);
weights.resize(n);
for (int i = 0; i < n; ++i) {
scanf("%d", &weights[i]);
}
vector<int> current_selection;
// 从第0个砝码开始,递归寻找所有保留 n-m 个砝码的组合
find_combinations(0, current_selection);
printf("%d\n", max_reachable_count);
return 0;
}
例题:P4377 [USACO18OPEN] Talent Show G
分析:最优比值问题,用 01 分数规划的思想二分答案。
问题变成了选出总重量至少为 \(W\) 的一些奶牛,使得 \(t - x \cdot w\) 的和大于等于 \(0\)。
可以用背包求出总重量为 \(i\) 的时候选出的和的最大值,特殊地,用 \(dp_W\) 表示总重量 \(\ge W\) 时的情况。
最后看 \(dp_W\) 是否 \(\ge 0\) 就可以了,整体时间复杂度为 \(O(nw\log t)\)。
参考代码
#include <cstdio>
#include <algorithm>
using std::max;
using ll = long long;
const int N = 255;
const int W = 1005;
const ll INF = 1e18;
int n, wlim, w[N], t[N];
ll dp[W];
bool check(int x) {
for (int i = 1; i <= wlim; i++) dp[i] = -INF;
for (int i = 1; i <= n; i++) {
ll value = t[i] - 1ll * w[i] * x;
for (int j = wlim; j >= max(0, wlim - w[i] + 1); j--)
if (dp[j] != -INF) dp[wlim] = max(dp[wlim], dp[j] + value);
for (int j = wlim; j >= w[i]; j--)
if (dp[j - w[i]] != -INF) dp[j] = max(dp[j], dp[j - w[i]] + value);
}
return dp[wlim] >= 0;
}
int main()
{
scanf("%d%d", &n, &wlim);
int l = 0, r = 0, ans = 0;
for (int i = 1; i <= n; i++) {
scanf("%d%d", &w[i], &t[i]); t[i] *= 1000;
r = max(r, t[i] / w[i]);
}
while (l <= r) {
int mid = (l + r) / 2;
if (check(mid)) {
l = mid + 1; ans = mid;
} else {
r = mid - 1;
}
}
printf("%d\n", ans);
return 0;
}
习题:AGC020C Median Sum
给定 \(N\) 个正整数,考虑由这 \(n\) 个数构成的所有 \(2^N-1\) 个非空子序列,并计算它们的和。将这些和从小到大排序后,得到序列 \(S\)。要求找出 \(S\) 的中位数,即第 \(2^{N-1}\) 个值。
问题分析
直接生成所有 \(2^N-1\) 个和是不可行的,因为 \(N\) 最大可达 \(2000\),需要利用问题的结构特性。
设所有输入数字 \(A_1, \dots, A_N\) 的总和为 \(\text{TotalSum}\)。
考虑所有 \(2^N\) 个子序列(包括空集),对于任意一个子序列,如果其元素和为 \(s\),那么它的补集(即在原集合中但不在该子序列中的元素)的和就是 \(\text{TotalSum}-s\)。
这意味着,由所有 \(2^N\) 个子序列(包括空集)的和构成的多重集,在数值上是关于 \(\dfrac{\text{TotalSum}}{2}\) 对称的。\(0\) 和 \(\text{TotalSum}\) 配对,\(A_1\) 和 \(\text{TotalSum}-A_1\) 配对,以此类推。
题目要求的是 \(2^N-1\) 个非空子序列和的中位数,即排序后的第 \(2^{N-1}\) 个数。
如果把空集的和 \(0\) 也加回来,得到一个包含 \(2^N\) 个数的多重集。在这个完整的多重集中,\(0\) 是最小的数。原序列的第 \(k\) 个数,在完整序列中是第 \(k+1\) 个数。因此,要找的原序列的第 \(2^{N-1}\) 个数,就是完整序列中的第 \(2^{N-1}+1\) 个数。
由于完整序列有 \(2^N\) 个数且对称,它的中位数(或中位区域)就在 \(\dfrac{\text{TotalSum}}{2}\) 附近。第 \(2^{N-1}\) 个数和第 \(2^{N-1}+1\) 个数是中间的两个数。要找的第 \(2^{N-1}+1\) 个数,正是这个对称序列中大于等于中轴线 \(\dfrac{\text{TotalSum}}{2}\) 的最小值。
所以,问题转化为:
- 找出所有可能凑出的子序列和。
- 在这些和中,找到大于或等于 \(\dfrac{\text{TotalSum}}{2}\) 的那个最小的和。
解题思路
找出所有可能的和是一个经典的动态规划问题,可以用 0/1 背包的模型来理解。一个高效的实现是使用 std::bitset,可以声明一个 bitset<MAX_SUM> bs,其中 bs[k] 为 1 表示 k 这个和是可以凑出的。
- 初始化:
bs[0] = 1,因为空集可以凑出 0 这个和。 - 状态转移:遍历每个输入的数 \(A_i\),对于每个 \(A_i\),更新
bs |= (bs << A[i])。bs << A[i]的含义是:将bs中所有为 1 的位向左移动A[i]。如果之前可以凑出s这个和(即bs[s] == 1),那么现在就可以凑出s + A[i]这个和。|=这个操作将这些凑出的和合并到bs中,表示这些和现在也成为可能。
完成所有数字的遍历后,bs 就记录了所有可能凑出的和。
根据之前的分析,中位数就是大于等于 \(\dfrac{\text{TotalSum}}{2}\) 的最小可行和。
- 在读入数字并进行
bitsetDP 的同时,累加计算出总和sum。 - DP 结束后,从
(sum + 1) / 2开始向上遍历,(sum + 1) / 2是 \(\left \lceil \dfrac{sum}{2} \right\rceil\) 在整数运算下的写法,保证了向上取整。 - 遇到的第一个满足
bs[i] == 1的i,就是要找的中位数,直接输出并结束。
设 \(M\) 为所有数字可能的最大总和(约为 \(2000 \times 2000 = 4 \times 10^6\)),那么时间复杂度为 \(O\left(\dfrac{NM}{\omega}\right)\),其中 \(\omega\) 是机器的字长(通常是 64)。bitset 的位运算是高度优化的,每次可以处理 \(\omega\) 位。
参考代码
#include <cstdio>
#include <bitset>
using namespace std;
const int N = 2005;
const int M = N * N; // 最大可能的总和
bitset<M> bs; // bs[k] = 1 表示可以凑出和为k
int main()
{
int n;
scanf("%d", &n);
int sum = 0; // 用于记录所有数字的总和
// 初始化:可以凑出和为0(空集)
bs[0] = 1;
// 动态规划:遍历每个数字,更新可以凑出的和
for (int i = 1; i <= n; i++) {
int x; scanf("%d", &x); sum += x;
// 核心转移:bs << x 表示在所有当前可凑出的和的基础上,都加上x
// bs |= ... 表示将这些新和合并到可行集里
bs |= (bs << x);
}
// 寻找中位数:
// 根据对称性,中位数是所有可行和中,大于等于 (sum/2) 的最小值。
// (sum + 1) / 2 是 ceil(sum / 2.0) 的整数实现,确保了向上取整。
for (int i = (sum + 1) / 2; i <= sum; i++) {
if (bs[i]) { // 找到第一个可凑出的和
printf("%d\n", i);
break; // 找到即退出
}
}
return 0;
}
多重背包问题
在 01 背包问题中,每种物品只能选 \(1\) 次,稍微扩展一下:现在允许一种物品选多次,规定第 \(i\) 种物品重量是 \(w_i\),价值是 \(v_i\),并且最多可以选 \(m_i\) 次。这类问题就叫做多重背包问题。注意,虽然一种物品是有多件的,但不一定要用,也不一定要用 \(m_i\) 次,可以随便选用几次。
例题:P1776 宝物筛选
一个简单的思路就是转化成熟悉的问题,想办法把多重背包问题转化成 01 背包问题。考虑到既然每种物品有 \(m_i\) 件,而这 \(m_i\) 件物品都是一样的重量和价格,可以随便取若干件。不妨将这种最多能用 \(m_i\) 次的物品,拆分成 \(m_i\) 种只能用一次的物品,如此一来就又回归 01 背包问题了。在 01 背包的代码基础之上加一层循环,对于第 \(i\) 种物品,加一层进行 \(m_i\) 次的循环,最里面还是正常循环背包容量。
参考代码
#include <cstdio>
#include <algorithm>
using std::max;
const int N = 105;
const int W = 4e5 + 5;
int v[N], w[N], m[N], dp[W];
int main()
{
int n, maxw; scanf("%d%d", &n, &maxw);
for (int i = 1; i <= n; i++) scanf("%d%d%d", &v[i], &w[i], &m[i]);
for (int i = 1; i <= n; i++) {
for (int cnt = 1; cnt <= m[i]; cnt++) { // 拆分成m[i]种只能用一次的物品
for (int j = maxw; j >= w[i]; j--) {
dp[j] = max(dp[j], dp[j - w[i]] + v[i]);
}
}
}
printf("%d\n", dp[maxw]);
return 0;
}
分析一下时间复杂度:总的虚拟的物品数量应该是 \(\sum m_i\),背包容量是 \(W\),则总的时间复杂度为 \(O(W \sum m_i)\),按照本题的数据范围,计算量是 \(4 \times 10^9\),会超时。
再考虑另外一种思路:多重决策。多重背包问题和 01 背包问题相比,主要的区别就在于:对于 01 背包问题中的前 \(i\) 个物品,当背包容量为 \(j\) 时,只有两种决策,要当前物品或者不要当前物品。但是在多重背包问题中,不止这两种决策,还可以选择某种物品要 \(2\) 次,要 \(3\) 次,……,要 \(m_i\) 次。这种决策方式,叫做多重决策。

对于 01 背包问题,当计算 \(dp_{i,j}\)(位置 A)的值时,它的值是从位置 B 和位置 C 转移过来的。但是对于多重背包问题,除了位置 B 和位置 C,可以继续考虑当前物品要 \(2\) 次,这时候 \(dp_{i,j} = dp_{i-1,j-2*w_i} + 2 * v_i\),即背包容量减掉当前物品 \(2\) 次的重量后,在前 \(i-1\) 个物品中能取到的最大价值,加上两倍当前物品的价值,即从位置 D 转移过来。同理,当前物品可以要 \(3\) 次、\(4\) 次,一直到 \(m_i\) 次,这些位置得到的值,最终取最大的一个就是 \(dp_{i,j}\)。状态转移方程为:\(dp_{i,j} = \max \{ dp_{i-1,j}, dp_{i-1,j-w_i}+v_i, dp_{i-1,j-2*w_i}+2*v_i, \cdots, dp_{i-1,j-m_i*w_i} + m_i*v_i \}\)。
当前,前提条件是背包容量 \(j\) 能够取当前物品 \(m_i\) 次。如果不够,背包容量除以物品重量的商,就是最大能取当前物品的次数。
参考代码
#include <cstdio>
#include <algorithm>
using std::max;
const int N = 105;
const int W = 4e5 + 5;
int v[N], w[N], m[N], dp[W];
int main()
{
int n, maxw; scanf("%d%d", &n, &maxw);
for (int i = 1; i <= n; i++) scanf("%d%d%d", &v[i], &w[i], &m[i]);
for (int i = 1; i <= n; i++) {
for (int j = maxw; j >= w[i]; j--) {
for (int cnt = 1; cnt <= m[i] && cnt * w[i] <= j; cnt++) {
dp[j] = max(dp[j], dp[j - cnt * w[i]] + cnt * v[i]);
}
}
}
printf("%d\n", dp[maxw]);
return 0;
}
注意两种思路的不同之处。多重决策算法的第 \(2\) 层循环是背包容量,第 \(3\) 层循环枚举当前物品要用几次。而第一种思路的第 \(2\) 层循环是将当前物品拆分成 \(m_i\) 种只能用 \(1\) 次的物品,第 \(3\) 层循环是背包容量。可以看到,这两种思路只是循环顺序交换了,计算量并没有很大的区别。因此,多重决策算法在本题的数据规模下,还是不能在时间限制内通过。
二进制拆分优化。不妨设当前物品的重量为 \(w\),价值为 \(v\),有 \(10\) 件,由于 \(10=1+2+4+3\),可以把这种有 \(10\) 件的物品,看成:
- 重量是 \(w\),价值是 \(v\) 的物品(称为 \(1\) 倍物品)\(1\) 件;
- 重量是 \(2w\),价值是 \(2v\) 的物品(称为 \(2\) 倍物品)\(1\) 件;
- 重量是 \(4w\),价值是 \(4v\) 的物品(称为 \(4\) 倍物品)\(1\) 件;
- 重量是 \(3w\),价值是 \(3v\) 的物品(称为 \(3\) 倍物品)\(1\) 件。
上面的 \(4\) 种物品都是只能使用 \(1\) 次的,这样就转化成了有 \(4\) 种物品的 01 背包问题,比优化前转换为 \(10\) 种物品的 01 背包问题物品更少,运行速度更快。这种拆分方法,是把物品的使用次数拆分成多个 \(2\) 的整数次幂的和的形式,拆分的过程特别像把十进制整数转换成二进制整数的过程,所以该优化方法叫做二进制拆分优化。
为什么这么做是正确的呢?考虑到在最优决策情况下,当前物品所有可能取到的次数是 \(0 \sim 10\) 之间的数,而用二进制拆分优化,所有 \(0 \sim 10\) 之间的整数,都能用这 \(4\) 个数字的相加表示出来。例如,\(3=1+2\),\(8=1+4+3\),\(10=1+2+4+3\),……。优化后总的时间复杂度降低为 \(O(W \sum \log m_i)\)。
参考代码
#include <cstdio>
#include <algorithm>
using std::max;
const int N = 105;
const int W = 4e5 + 5;
int v[N], w[N], m[N], dp[W];
int main()
{
int n, maxw; scanf("%d%d", &n, &maxw);
for (int i = 1; i <= n; i++) scanf("%d%d%d", &v[i], &w[i], &m[i]);
for (int i = 1; i <= n; i++) {
for (int cnt = 1; cnt <= m[i]; cnt *= 2) {
// 当前考虑cnt倍物品,每次循环翻倍,相当于依次枚举1倍物品,2倍物品,4倍物品,……
for (int j = maxw; j >= cnt * w[i]; j--) {
// 此时物品的重量是cnt*w[i],价值cnt*v[i]
dp[j] = max(dp[j], dp[j - cnt * w[i]] + cnt * v[i]);
}
m[i] -= cnt; // 从总数m[i]里减掉cnt
}
for (int j = maxw; j >= m[i] * w[i]; j--) { // 最后剩下一个m[i]倍物品
dp[j] = max(dp[j], dp[j - m[i] * w[i]] + m[i] * v[i]);
}
}
printf("%d\n", dp[maxw]);
return 0;
}
完全背包问题
01 背包问题是每种物品最多取一次,多重背包问题是每种物品有多件,但是限制了最多使用次数。如果进一步扩展,每种物品的数量都是无限多,这类问题就叫做完全背包问题。
如果还是考虑转化成 01 背包问题,由于背包容量 \(C\) 是有限的,即便物品可以取无限次,但是实际上对于重量为 \(w_i\) 的物品,能取的次数最多是 \(C/w_i\) 次,物品再多背包也装不下了。这样一来,问题就可以转化为多重背包问题。
如果按照多重决策的做法,那么对于每个物品来说,决策就不止取或者不取,而是可以选择:不取,取 \(1\) 次,取 \(2\) 次,取 \(3\) 次,……,直到背包装不下,类似的状态转移方程:\(dp_{i,j} = \max \{ dp_{i-1,j}, dp_{i-1,j-w}+v, dp_{i-1,j-2w}+2v, dp_{i-1, j-3w}+3v, \cdots \}\)。
也就是在计算 \(dp_{i,j}\) 时,需要循环 \(j/w\) 次,去枚举每种可能性,最后找最大价值。这样做时间复杂度较高,能否优化?
注意,在求 \(dp_{i,j}\) 之前,已经计算完 \(dp_{i,j-w}\) 这个位置的值了:\(dp_{i,j-w} = \max \{ dp_{i-1,j-w}, dp_{i-1,j-2w}+v, dp_{i-1,j-3w}+2v, dp_{i-1,j-4w}+3v, \cdots \}\)。
可以看出,当计算 \(dp_{i,j}\) 时,从第 \(2\) 项开始,每一项都是跟 \(dp_{i,j-w}\) 对应的,只是相差了一个 \(v\) 而已,所以没有必要去计算这些项的最大值,它们的最大值就等于 \(dp_{i,j-w}+v\)。
因此,在计算 \(dp_{i,j}\) 时就没必要用循环了,可以得到:\(dp_{i,j} = \max \{ dp_{i-1,j}, dp_{i,j-w}+v \}\)。
再回顾一下 01 背包问题的状态转移方程:\(dp_{i,j} = \max \{ dp_{i-1,j}, dp_{i-1,j-w}+v \}\)。
可以看到,几乎一样,只不过 01 背包问题是从上一行的位置 \(j\) 和位置 \(j-w\) 转移的,而完全背包问题是从上一行的位置 \(j\) 和当前行的位置 \(j-w\) 转移的。

要求的是 \(dp_{i,j}\) 的值(位置 A),如果是 01 背包问题,它的值从位置 B 和位置 C 转移;如果是完全背包问题,它的值从位置 B 和位置 D 转移。
注意,位置 C 是上一行的第 \(j\) 列,而位置 D 是当前行的第 \(j\) 列。这个结论也可以理解成:因为完全背包问题中物品相当于有无限件,可以从上一次拿过这种物品的位置转移,看看是否可以再拿一次。
这样,完全背包问题的代码和 01 背包问题的代码非常接近。考虑能否压缩到一维空间?01 背包问题如果要用一维数组,需要把背包容量的循环按从大到小的顺序进行。因为每次计算均依赖左边的值,必须保证左边的值还没被覆盖成当前物品的值。而完全背包问题的状态转移方程就是要使用当前行左边的值,被覆盖成之后的值正好接下来就要使用,所以完全背包问题压缩空间后的代码,只需要把 01 背包问题代码中背包容量的循环改成正序。
例题:P1616 疯狂的采药
参考代码
#include <cstdio>
#include <algorithm>
using ll = long long;
using std::max;
const int M = 1e4 + 5;
const int T = 1e7 + 5;
int a[M], b[M];
ll dp[T];
int main()
{
int t, m; scanf("%d%d", &t, &m);
for (int i = 1; i <= m; i++) scanf("%d%d", &a[i], &b[i]);
for (int i = 1; i <= m; i++) {
for (int j = a[i]; j <= t; j++) {
dp[j] = max(dp[j], dp[j - a[i]] + b[i]);
}
}
printf("%lld\n", dp[t]);
return 0;
}
例题:P1679 神奇的四次方数
这个问题可以转化成背包问题。因为要把整数 \(m\) 分解成四次方数相加的形式,可以把每个四次方数看作物品,将四次方数的大小看作物品的重量,物品的价值则都是 \(1\),因为选一次就代表多了一个数字。最终要凑成的整数 \(m\) 可看作背包的容量。需要在背包容量正好用光的情况下,找到最小总价值。
对于每个四次方数,可以不选,也可以使用无限次,显然这是一个完全背包问题。由于希望使用的数字数量尽可能少,所以 \(dp\) 数组要初始化为最大值,考虑到任何一个数 \(x\) 都起码可以拆分为 \(x\) 个 \(1^4\) 相加,因此可初始化 \(dp_i = i\)。而一开始总和 \(0\) 是可以构成的,且不需要数字,所以 \(dp_0 = 0\)。
参考代码
#include <cstdio>
#include <algorithm>
using std::min;
const int M = 1e5 + 5;
int dp[M];
int main()
{
int m; scanf("%d", &m);
for (int i = 1; i <= m; i++) {
dp[i] = i;
}
for (int i = 1; i * i * i * i <= m; i++) {
int num = i * i * i * i;
for (int j = num; j <= m; j++) {
dp[j] = min(dp[j], dp[j - num] + 1);
}
}
printf("%d\n", dp[m]);
return 0;
}
习题:P6567 [NOI Online #3 入门组] 买表
问题分析
从题面来看这是一个典型的多重背包问题,有 \(n\) 种物品(钱币),每种物品的重量(面额)是 \(k_i\),数量是 \(a_i\)。需要判断对于一系列给定的背包容量,是否能恰好装满背包。
解题思路
可以使用动态规划来解决这个问题。
定义一个布尔数组 \(dp_j\),其中 \(dp_j\) 等于 true 表示总面额为 \(j\) 的钱可以被凑出,\(dp_j\) 等于 false 表示无法凑出,目标是计算出所有可能凑出的面额。
初始化 \(dp_0\) 为 true,因为总额为 0 是唯一不需要任何钱币就能“凑出”的金额,数组其余部分初始化为 false。
依次考虑每一种钱币 \((k_i, a_i)\),并用它来更新 \(dp\) 数组。对于一种钱币,它可以用来凑出新的面额。
一个面额 \(j\) 如果能被凑出,那么它一定是由一个更小的、已经能凑出的面额 \(j - k_i\) 再加上一张面额为 \(k_i\) 的钱币得到的。
但是,每种钱币的数量 \(a_i\) 是有限的,这正是多重背包问题的核心。为了处理数量限制,不能简单地像完全背包那样更新 \(dp\) 数组。
可以使用一个巧妙的方法来处理数量限制,在遍历每种钱币 \((k,a)\) 时:
- 使用一个辅助数组 \(used_j\) 来记录凑成金额 \(j\) 连续使用了多少张当前种类的钱币 \(k\)。
- 状态转移方程:如果 \(dp_{j-k}\) 为
true(即 \(j-k\) 是一个能凑出的金额),并且凑出 \(j-k\) 所使用的当前钱币数量 \(used_{j-k}\) 小于该钱币的总数 \(a\),那么就可以再加一张 \(k\) 元钱币来凑出金额 \(j\)。这种情况下,\(dp_j\) 可以设为true,并更新 \(used_j\) 为 \(used_{j-k}+1\)。 - 注意如果 \(dp_j\) 在尝试更新之前已经是
true了,说明 \(j\) 这个金额已经被之前的钱币组合凑出来了,就没必要再计算了,因为只关心“能不能凑出”,而不是“有几种解法”,这种情况下相当于保持 \(used_j\) 为 0,可以让更大的面额更有可能被凑出来。
在处理完所有 \(n\) 种钱币后,\(dp\) 数组就包含了所有能凑出的金额的信息。对于每个查询的手表价格 \(t\),只需检查 \(dp_t\) 的值。如果为 true,则可以购买,输出 Yes,否则输出 No。因此 DP 数组大小是根据题目数据范围 \(t_i \le 500000\) 来确定的。
算法的时间复杂度为 \(O(n T_{max})\),其中 \(T_{max}\) 是最大价格。对于本题的数据范围,约为 \(10^8\),可以在 1s 的时间限制内通过。
参考代码
#include <cstdio>
#include <vector> // 使用 vector 作为辅助数组
using namespace std;
// dp[j] 记录金额 j 是否能够被凑出
bool dp[500005];
int main()
{
int n, m;
scanf("%d%d", &n, &m);
// 初始化:金额0可以被凑出(不需要任何钱币)
dp[0] = true;
// 辅助数组,记录在当前钱币种类下,凑成金额 j 所使用的该钱币的张数
vector<int> used(500001);
// 遍历 n 种钱币,这是一个多重背包问题
for (int i = 0; i < n; i++) {
int k, a; // k 是面额,a 是张数
scanf("%d%d", &k, &a);
// 每处理一种新钱币,就重置 used 数组
used.assign(500001, 0);
// 遍历所有可能的金额 j,尝试用当前钱币 k 去更新 dp 数组
// j 从 k 开始,因为小于 k 的金额不可能由 j-k 转移而来
for (int j = k; j <= 500000; j++) {
// 状态转移:
// 1. !dp[j]: 优化,如果 j 已经能凑出,就不用再计算了
// 2. dp[j-k]: 金额 j-k 是可以凑出的
// 3. used[j-k] < a: 凑成 j-k 后,当前种类的钱币还有剩余
if (!dp[j] && dp[j - k] && used[j - k] < a) {
// 金额 j 可以被凑出
dp[j] = true;
// 更新凑成 j 所使用的当前钱币的数量
used[j] = used[j - k] + 1;
}
}
}
// 处理 m 个查询
for (int i = 0; i < m; i++) {
int t; // 手表价格
scanf("%d", &t);
// 查询 dp 数组,判断价格 t 是否能被凑出
if (dp[t]) printf("Yes\n");
else printf("No\n");
}
return 0;
}
习题:P5020 [NOIP 2018 提高组] 货币系统
问题分析
从原来的 \(n\) 种面额中,选出一个尽可能小的子集,让这个子集能凑出原来的 \(n\) 种面额。
例如,原来的货币是 \(\{ 3,10,6,19 \}\),其中 \(6\) 可以用两个 \(3\) 凑出来,\(19\) 可以用一个 \(10\) 和三个 \(3\) 凑出来。所以 $$6$ 和 \(19\) 就是多余的,只需要保留 \(\{ 3,10 \}\),就能表示出原来系统能表示的所有金额。所以,最简的系统面额数量就是 \(2\)。
最终目标就是找出所有“不可替代”的“本质”面额的数量。
解题思路
怎么判断一个面额 \(a_i\) 是不是“本质”的呢?就看它能否被其它面额凑出来,如果能,它就是“冗余”的;如果不能,它就是“本质”的。
先把所有面额从小到大排个序,排序之后,当判断 \(a_i\) 能不能被“其它”面额凑出来时,还需要考虑比 \(a_i\) 大的面额吗?显然不用,因为所有面额都是正数,用一个比 \(a_i\) 还大的数,是不可能凑出 \(a_i\) 的。所以,只需要考虑比 \(a_i\) 小的那些面额能不能凑出 \(a_i\) 就行了。
“一个数能否被一堆数凑出来”,这正是背包问题的变种,可以用动态规划来解决。
定义一个布尔数组,\(dp_j\) 等于 true 表示金额 \(j\) 可以被已经找到的那些“本质”面额凑出来。
在排序后看每一个面额 \(a_i\),如果 \(dp_{a_i}\) 为 true,说明这个 \(a_i\) 是由更小的那些“本质”面额更新过的,那么 \(a_i\) 就是一个冗余的面额。
如果 \(dp_{a_i}\) 是 false,\(a_i\) 就是一个“本质”面额,它无法被更小的面额替代。同时因为它也是一个可用的面额,需要用它去更新 \(dp\) 数组,看看加上它之后,又能凑出哪些新的金额。这个更新过程,就是一个完全背包问题。
参考代码
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 105; // n 的最大值
const int A = 25005; // a[i] 的最大值
int a[N];
bool dp[A]; // dp[j] = true 的意思是:金额 j 可以被凑出来
int main()
{
int t;
scanf("%d", &t);
while (t--) {
int n; // n种面额
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]);
}
sort(a + 1, a + n + 1);
for (int i = 1; i <= a[n]; i++) dp[i] = false;
dp[0] = true; // 金额0不需要任何货币就能凑出
int ans = n;
for (int i = 1; i <= n; i++) {
if (dp[a[i]]) {
// 如果已经是 true,说明 a[i] 这个金额可以被比它更小的货币凑出来。
ans--;
continue;
}
for (int j = a[i]; j <= a[n]; j++) {
// 如果金额 j-a[i] 能凑出来,那 j 肯定也能凑出来(在 j-a[i] 的基础上再加个 a[i] 就行了)
dp[j] |= dp[j - a[i]];
}
}
printf("%d\n", ans);
}
return 0;
}
习题:P5662 [CSP-J2019] 纪念品
解题思路
题目的核心是在 \(T\) 天内通过买卖 \(N\) 种纪念品来最大化最终的金币数,一个关键信息是“每天可以进行两种交易无限次”。
这个“无限次”交易的规则非常重要,它意味着在任何一天 \(i\),你持有的所有金币和纪念品可以自由地相互转换。例如,你可以把所有钱换成纪念品 A,再立刻换成纪念品 B,或者换回金币。这说明在当天,所有资产(金币 + 纪念品)的价值是等效的,可以统一用金币衡量。假设你打算“在第 2 天买进,第 4 天卖出”,等价于“第 2 天买进,第 3 天卖出,第 3 天立马买进,第 4 天再卖出”。
因此,整个问题可以分解成 \(T-1\) 个独立的决策阶段。在每一天 \(i\) 的开始(对应前一天 \(i-1\) 结束时),拥有一定的资金,目标是决定如何用这些资金投资(购买当天的纪念品),以便在第二天 \(i+1\) 卖出后,拥有的总资金最多。
对于每一个决策阶段(从第 \(i\) 天到第 \(i+1\) 天),面临的问题可以抽象为一个经典的完全背包问题。
- 背包容量:在第 \(i\) 天开始时拥有的总金币数 \(M\)。
- 物品:当天可以购买的 \(N\) 种纪念品。
- 每种物品 \(j\) 的属性
- 体积:在第 \(i\) 天购买物品 \(j\) 的价格 \(P_{i,j}\)。
- 价值:这次投资能带来的净利润,即在第 \(i+1\) 天卖出的价格 \(P_{i+1,j}\) 减去第 \(i\) 天购买它的成本 \(P_{i,j}\)。所以,价值为 \(P_{i+1,j} - P_{i,j}\)。
- 目标:在总花费不超过总资金 \(M\) 的前提下,最大化总利润。
因为每种纪念品可以购买无限个(只要钱够),所以这是一个完全背包模型,而不是 0/1 背包。
参考代码
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 105; // 最大天数和物品种类
const int P = 10005; // 最大金币数 (背包容量)
int p[N][N]; // p[i][j]: 第 i 天第 j 种纪念品的价格
int dp[P]; // dp[k]: 在一个决策阶段中,花费k元能获得的最大净利润
int main()
{
int t, n, m; // t:天数, n:纪念品种类, m:初始金币
scanf("%d%d%d", &t, &n, &m);
// 读取所有价格数据
for (int i = 1; i <= t; i++) {
for (int j = 1; j <= n; j++) scanf("%d", &p[i][j]);
}
// 外层循环:遍历 t-1 个投资阶段 (从第 i 天到第 i+1 天)
for (int i = 1; i < t; i++) {
// --- 开始一轮完全背包计算 ---
// 初始化dp数组,对于当前 i -> i+1 阶段,利润全部从0开始计算
for (int j = 0; j <= m; j++) dp[j] = 0;
// 遍历 N 种物品
for (int j = 1; j <= n; j++) {
// 遍历背包容量(金币),从物品j的花费开始,正序遍历
for (int k = p[i][j]; k <= m; k++) {
// 状态转移方程:dp[k] = max(不买j, 买了j)
// 买了j的利润 = 用 k-p[i][j] 的钱能获得的最大利润 + 买j本身获得的利润
// 买j本身的利润 = p[i+1][j] - p[i][j]
dp[k] = max(dp[k], dp[k - p[i][j]] + p[i + 1][j] - p[i][j]);
}
}
// --- 完全背包计算结束 ---
// 当天投资结束后,用现有全部资金m能获得的最大利润是dp[m]
// 更新总资金,作为下一天的起始资金
m += dp[m];
}
// 经过 t-1 天的投资,最终在第 t 天拥有的金币数就是答案
printf("%d\n", m);
return 0;
}
习题:P1941 [NOIP 2014 提高组] 飞扬的小鸟
解题思路
一、状态定义
一个很自然的想法,\(dp_{i,j}\) 表示小鸟在横坐标为 \(i\)、高度为 \(j\) 时,所需要的最少点击次数。
目标是求出所有合法的 \(j\) 的最小 \(dp_{n,j}\)。
二、状态转移分析
小鸟从横坐标 \(i-1\) 移动到 \(i\) 时,有两种操作:
- 下降:如果不点击屏幕,小鸟会从 \((i-1, j+y_i)\) 下降到 \((i,j)\)。这种转移不增加点击次数。这里的转移相当于 0/1 背包。
- 上升:这种情况相对更复杂,因为“可以点击多次”,是典型的完全背包问题。
\(dp_{i,j}\) 取这两种情况的最小值。
三、混合背包模型
这里有一个深刻的问题:正确的处理顺序是先处理上升(完全背包),再处理下降(0/1 背包)。顺序不能调换,原因在于两种操作的依赖关系和状态定义。
下降操作(0/1 背包)依赖于 \(i-1\) 列的最终、完整的最优解。而上升操作(完全背包)会在 \(i\) 列内部进行递推,它会“污染”当前列的状态。
如果先处理下降,再处理上升,处理上升时用到的当前列的状态已经是考虑了下降操作后的结果,在这个结果上跑完全背包的转移更新过程相当于允许上升效果和下降效果进行叠加,而按照题意,每次屏幕操作是只能选一种的。
四、代码实现细节
- 边界:如果小鸟上升后高度超过 \(m\),它会停在 \(m\) 处。也就是说 \(m-x_i\) 到 \(m\) 经过上升后都会转移到 \(m\) 这个高度状态上。
- 管道:管道覆盖对状态转移的影响在本题中要特别注意。正确的处理方式应该是在跑完全背包和 0/1 背包之前,先不考虑管道的存在,等前面的转移计算完成之后,再将管道覆盖的位置标记为不可达状态。
- 核心原因:必须区分“路径的中间点”和“路径的终点”。
- 一个在管道内的位置,虽然不能作为小鸟停留的最终位置,但它完全可以作为一个计算过程中的“虚拟跳板”或“中间状态”,用于推导出其他合法位置的解。如果在计算转移的一开始就将管道位置标记为不可达,就会错误地切断所有“飞跃”管道的路径。
- 最后将管道标记为不可达,是施加一个最终状态的约束。这个约束必须在所有可能性(路径)都计算完毕后才能施加。
参考代码
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 10005;
const int M = 1005;
const int INF = 1e9;
int up[N], down[N], low[N], high[N], dp[2][M];
bool pipe[N];
int main() {
int n, m, k;
scanf("%d%d%d", &n, &m, &k);
for (int i = 1; i <= n; i++) {
scanf("%d%d", &up[i], &down[i]);
low[i] = 0;
high[i] = m + 1;
}
for (int i = 1; i <= k; i++) {
int h, l, p;
scanf("%d%d%d", &h, &l, &p);
low[h] = l; high[h] = p; pipe[h] = true;
}
int cnt = 0;
bool ok = true;
for (int i = 1; i <= n; i++) {
// init
int cur = i % 2, pre = 1 - cur;
for (int j = 0; j <= m; j++) dp[cur][j] = INF;
// up: +up
for (int j = 0; j <= m; j++) { // 管道位置要先当成可达状态
int from = j - up[i];
if (from > 0 && dp[pre][from] != INF) dp[cur][j] = min(dp[cur][j], dp[pre][from] + 1);
if (from > 0 && dp[cur][from] != INF) dp[cur][j] = min(dp[cur][j], dp[cur][from] + 1);
}
// top
if (high[i] == m + 1) {
for (int j = m - up[i]; j <= m; j++) {
if (dp[pre][j] != INF) dp[cur][m] = min(dp[cur][m], dp[pre][j] + 1);
if (dp[cur][j] != INF) dp[cur][m] = min(dp[cur][m], dp[cur][j] + 1);
}
}
// down: -down
// 下降的0/1背包在上升的完全背包之后计算
for (int j = high[i] - 1; j >= low[i] + 1; j--) {
int from = j + down[i];
if (from <= m && dp[pre][from] != INF) dp[cur][j] = min(dp[cur][j], dp[pre][from]);
}
// check
bool flag = false;
for (int j = low[i] + 1; j <= high[i] - 1; j++) {
if (dp[cur][j] != INF) {
flag = true;
break;
}
}
if (!flag) {
ok = false;
printf("0\n%d\n", cnt);
break;
}
if (pipe[i]) cnt++;
for (int j = 0; j <= low[i]; j++) dp[cur][j] = INF;
for (int j = high[i]; j <= m; j++) dp[cur][j] = INF;
}
if (ok) {
printf("1\n");
int ans = INF;
for (int i = low[n] + 1; i <= high[n] - 1; i++) ans = min(ans, dp[n % 2][i]);
printf("%d\n", ans);
}
return 0;
}
习题:P1450 [HAOI2008] 硬币购物
解题思路
初看题面,这是一个典型的多重背包问题。但是,对于每一组查询都重新跑一次多重背包会超时。
因此需要转换思路,问题的难点在于硬币数量的上限。如果去掉这个上限,问题就变成了完全背包问题:用 4 种面值的硬币(数量无限)凑成金额 \(s\) 有多少种方案?
这个无限制的问题可以很容易地用动态规划解决,而且只需要计算一次,就能得到凑成任意金额的方案数。
定义 \(dp_i\) 表示用 4 种硬币(数量无限)凑成金额 \(i\) 的方案数。跑完完全背包后,\(dp_s\) 就存储了用无限多的硬币凑成金额 \(s\) 的总方案数。
现在有了总方案数 \(dp_s\),但这里面包含了很多不合法的方案(即某些硬币用得超过了 \(d_i\) 的限制),需要从总方案数中减去这些不合法的方案。
直接减去不合法的方案很复杂,因为一个方案可能同时违反了多个限制(比如硬币 1 和硬币 2 都用超了)。这是,容斥原理就派上了用场。
设 \(S\) 为总方案集(无限制),\(A_i\) 为使用第 \(i\) 种硬币超过 \(d_i\) 枚的方案集。要求的就是:\(|S| - |A_1 \cup A_2 \cup A_3 \cup A_4|\)。根据容斥定理,这个式子展开之后就是总方案减去至少违反一个限制的,加上至少违反两个限制的,减去至少违反三个限制的,加上违反全部四个限制的。
那么如何计算 \(|A_i|, |A_1 \cap A_2|\) 诸如此类这样的集合的大小呢?
- 计算 \(|A_i|\):\(A_i\) 是指第 \(i\) 种硬币至少用了 \(d_i + 1\) 枚的方案集。可以想象,先强制性地拿出 \(d_i+1\) 枚第 \(i\) 种硬币,支付的金额为 \(c_i \cdot (d_i + 1)\)。剩下的金额 \(s - c_i \cdot (d_i + 1)\) 可以用任意无限多的硬币来凑。这个方案数正好就是预处理好的 \(dp_{s - c_i \cdot (d_i + 1)}\)。所以 \(|A_i| = dp_{s - c_i \cdot (d_i+1)}\)。
- 计算 \(|A_i \cap A_j|\):同理,这是指第 \(i\) 种硬币至少用 \(d_i + 1\) 枚,且第 \(j\) 种硬币至少用 \(d_j+1\) 枚。先强制拿出这些硬币,剩下的金额的凑法数量就是 \(dp_{s - c_i \cdot (d_i + 1) - c_j \cdot (d_j+1)}\)。
参考代码
#include <cstdio>
typedef long long LL;
const int S = 100005;
int c[5], d[5], s;
LL dp[S], tmp, ans;
LL calc(int i) {
return 1ll * (d[i] + 1) * c[i];
}
void update(int flag) {
if (tmp <= s) ans += dp[s - tmp] * flag;
}
int main()
{
int n;
for (int i = 1; i <= 4; i++) scanf("%d", &c[i]);
scanf("%d", &n);
dp[0] = 1;
for (int i = 1; i <= 4; i++) {
for (int j = c[i]; j < S; j++) {
dp[j] += dp[j - c[i]];
}
}
while (n--) {
for (int i = 1; i <= 4; i++) scanf("%d", &d[i]);
scanf("%d", &s); ans = dp[s];
tmp = calc(1); update(-1);
tmp = calc(2); update(-1);
tmp = calc(3); update(-1);
tmp = calc(4); update(-1);
tmp = calc(1) + calc(2); update(1);
tmp = calc(1) + calc(3); update(1);
tmp = calc(1) + calc(4); update(1);
tmp = calc(2) + calc(3); update(1);
tmp = calc(2) + calc(4); update(1);
tmp = calc(3) + calc(4); update(1);
tmp = calc(1) + calc(2) + calc(3); update(-1);
tmp = calc(1) + calc(2) + calc(4); update(-1);
tmp = calc(1) + calc(3) + calc(4); update(-1);
tmp = calc(2) + calc(3) + calc(4); update(-1);
tmp = calc(1) + calc(2) + calc(3) + calc(4); update(1);
printf("%lld\n", ans);
}
return 0;
}
习题:P13349 「ZYZ 2025」自然数序列
解题思路
题目的核心是求解一个带约束的计数问题。对于每次查询,要求解一个不定方程组的非负整数解的数量:
- \(a_1 b_1 + a_2 b_2 + \cdots + a_n b_n = S\),其中 \(S\) 在 \([l,r]\) 区间内。
- 有 \(k\) 个附加条件,形如 \(b_x = y\)。
注意到查询虽然多,但基础的“物品”序列即 \(a_i\) 是不变的,而附加限制的数量 \(k\) 非常小(\(k \le 8\)),这给出了一定的启示:先预处理,然后针对少量限制使用一些数学技巧求解。
第一步:预处理 —— 无限制的完全背包
首先,忽略所有的限制条件,只考虑问题:用 \(n\) 种物品,第 \(i\) 种物品的“体积”为 \(a_i\),每种物品可以无限次使用,凑成总体积恰好为 \(j\) 的方案数有多少?
这是一个经典的完全背包问题。先预处理出 \(dp_j\) 表示用全部 \(n\) 种物品凑成体积 \(j\) 的方案数。
第二步:预处理 —— 前缀和优化区间查询
题目要求总和在 \([l, r]\) 区间内,而不是一个固定的值。为了能快速查询一个区间的方案数,对 \(dp\) 数组再做一次预处理,计算出它的前缀和。
第三步:处理查询 —— 利用容斥原理
- 处理固定限制:对于每个限制 \(b_x = y\),这部分是确定的。它们贡献的总和是 \(\sum a_x y\)。将所有 \(k\) 个限制贡献的总和加起来,然后从目标区间 \([l, r]\) 中减掉,得到新的目标区间 \([l', r'] = [l - \sum a_x y, r - \sum a_x y]\)。
- 转化问题:现在问题变成了对于那 \(k\) 个被限制的物品,不能自由选择它们了(因为它们的数量已经被固定,贡献已经在目标区间中扣除)。需要用剩下 \(n-k\) 个无限制的物品,凑出在 \([l', r']\) 区间内的体积。但是,预处理的 \(dp\) 数组是基于全部 \(n\) 个物品的。如何从中得到只用 \(n-k\) 个物品的结果呢?
- 容斥原理:直接“撤销” \(k\) 个物品对 \(dp\) 数组的贡献很困难。但因为 \(k\) 很小,可以使用容斥原理。目标是计算只是用无限制物品的方案数,这等价于 \(使用全部物品的方案数 - 至少使用1个被限制物品的方案数 + 至少使用2个被限制物品的方案数 - \cdots\)。
- 总方案数:用全部 \(n\) 个物品凑成 \([l',r']\) 的方案数,相当于直接查询区间和。
- 减去一项:对于某个被限制的物品 \(x\),要减去“至少用了一次 \(a_x\)”的方案数。这可以通过先强制用一个 \(a_x\),然后用全部 \(n\) 个物品去凑剩下的体积 \([l' - a_x, r' - a_x]\) 来计算。
- 加上两项:对于被限制的物品 \(x_1\) 和 \(x_2\),减去了两次它们俩都被用上的情况,所以要加回来一次。相当于凑 \([l' - a_{x_1} - a_{x_2}, r' - a_{x_1} - a_{x_2}]\)。
- ……
- 这个过程可以通过遍历 \(k\) 个限制物品的所有 \(2^k\) 个子集来完成
参考代码
#include <cstdio>
#include <vector>
using namespace std;
using ll = long long;
const int MOD = 998244353;
int main()
{
int n, q; scanf("%d%d", &n, &q);
vector<int> a(n + 1), dp(5001);
dp[0] = 1;
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]);
for (int j = a[i]; j <= 5000; j++) {
dp[j] = (dp[j] + dp[j - a[i]]) % MOD;
}
}
for (int i = 1; i <= 5000; i++) dp[i] = (dp[i] + dp[i - 1]) % MOD;
auto query = [&](int l, int r) {
int high = r >= 0 ? dp[r] : 0;
int low = l >= 1 ? dp[l - 1] : 0;
return (high + MOD - low) % MOD;
};
while (q--) {
int l, r, k; scanf("%d%d%d", &l, &r, &k);
vector<int> pos;
for (int i = 0; i < k; i++) {
int x, y; scanf("%d%d", &x, &y);
pos.push_back(x);
l -= a[x] * y; r -= a[x] * y;
}
int ans = 0;
for (int i = 0; i < (1 << k); i++) {
int sum = 0, add = 1;
for (int j = 0; j < k; j++) {
if ((i >> j) & 1) {
sum += a[pos[j]];
add ^= 1;
}
}
if (add) ans = (ans + query(l - sum, r - sum)) % MOD;
else ans = (ans + MOD - query(l - sum, r - sum)) % MOD;
}
printf("%d\n", ans);
}
return 0;
}
分组背包问题
前面介绍的 01 背包问题、多重背包问题和完全背包问题,物品之间都没有关系。一种物品要不要,要几个,都不会影响其他物品的选取。如果物品之间相互影响,比如所有的物品分为 \(k\) 组,每组内最多只能选一种物品,这样的问题就叫做分组背包问题。
分组背包问题比较好解决,假设所有的物品分为 \(k\) 组,第 \(1\) 组物品中包含 \(n_1\) 种不同的物品,第 \(2\) 组物品中包含 \(n_2\) 种不同的物品,……,第 \(k\) 组物品中包含 \(n_k\) 种不同的物品,每种物品都只能要一次。不妨把每组看作一个大的物品,决策方式是:不要,要组内第 \(1\) 种物品,要组内第 \(2\) 组物品,……,要组内第 \(n_1\) 种物品。再去看第 \(2\) 组,以此类推。设 \(dp_{i,j}\) 表示只考虑前 \(i\) 组物品,且背包容量为 \(j\) 时,能拿到物品的最大价值,则有:\(dp_{i,j} = \max \{ dp_{i-1,j}, dp_{i-1,j-w_1}+v_1, dp_{i-1,j-w_2}+v_2, \cdots, dp_{i-1,j-w_{n_k}} + v_{n_k} \}\)。
式中,\(w_1, w_2, \cdots, w_{n_k}\) 表示组内每种物品的重量,\(v_1, v_2, \cdots, v_{n_k}\) 表示组内每种物品的价值。
伪代码如下:
当前枚举第k组:
倒序枚举背包容量,目前容量为j:
对于每个属于第k组的物品i:
dp[j] = max(dp[j], dp[j - w[i]] + v[i])
例题:P1064 [NOIP2006 提高组] 金明的预算方案
首先明确物品的价值是什么,按照本题的定义,每个物品的价值是它的价格和重要度的乘积。所以在输入物品信息时,可以提前计算好这个价值,存在数组里面。而每个物品的价格,其实就相当于 01 背包问题里每个物品的重量,总的花费相当于背包容量。
另外,本题是有依赖的情况,如果要购买附件,就必须购买主件。这个依赖关系可以转化成分组背包问题。对于每个主件,最多有 \(2\) 个附件,因此,所有的购买情况包括:全都不要,只要主件,要主件和 \(1\) 号附件,要主件和 \(2\) 号附件,要主件和 \(1\) 号、\(2\) 号附件,共计 \(5\) 种情况。那么对于一个主件和它的附件,可以创建 \(4\) 个虚拟物品:
- 第 \(1\) 个虚拟物品表示只要主件的情况,它的价值对应主件的价值,它的重量对应主件的价格。
- 第 \(2\) 个虚拟物品表示要主件和 \(1\) 号附件的情况,它的价值对应主件和 \(1\) 号附件的价值之和,它的重量对应主件和 \(1\) 号附件的价格之和。
- 第 \(3\) 个虚拟物品表示要主件和 \(2\) 号附件的情况,它的价值对应主件和 \(2\) 号附件的价值之和,它的重量对应主件和 \(2\) 号附件的价格之和。
- 第 \(4\) 个虚拟物品表示要主件和 \(2\) 个附件的情况,它的价值对应主件和 \(2\) 个附件的价值之和,它的重量对应主件和 \(2\) 个附件的价格之和。
上述 \(4\) 个虚拟物品,最多只能选一个,或者一个都不选,可以把这 \(4\) 个物品看成是一个分组里的。这样一来,每个主件及其附件的依赖关系,就转化成了分组背包问题,可以套用之前的模型来计算。
参考代码
#include <cstdio>
#include <vector>
#include <algorithm>
using std::max;
using std::vector;
const int M = 65;
const int N = 32005;
int v[M], p[M], q[M], dp[N];
vector<int> accessories[M];
void update(int cap, int weight, int value) {
if (cap >= weight) dp[cap] = max(dp[cap], dp[cap - weight] + value);
}
int main()
{
int n, m; scanf("%d%d", &n, &m);
for (int i = 1; i <= m; i++) {
scanf("%d%d%d", &v[i], &p[i], &q[i]); // v[i]为价格
p[i] *= v[i]; // 价格和重要度的乘积
if (q[i] != 0) accessories[q[i]].push_back(i); // 如果是附件,在其主件处记录该附件的编号
}
for (int i = 1; i <= m; i++) {
if (q[i] == 0) { // 每个主件代表一组物品
for (int j = n; j >= 0; j--) { // 枚举背包容量
update(j, v[i], p[i]); // 只使用主件
if (accessories[i].size() > 0) { // 如果有附件
int acs = accessories[i][0];
update(j, v[i] + v[acs], p[i] + p[acs]); // 主件+附件1
}
if (accessories[i].size() > 1) { // 如果不止1个附件
int acs1 = accessories[i][0], acs2 = accessories[i][1];
// 主件+附件2
update(j, v[i] + v[acs2], p[i] + p[acs2]);
// 主件+2个附件
update(j, v[i] + v[acs1] + v[acs2], p[i] + p[acs1] + p[acs2]);
}
}
}
}
printf("%d\n", dp[n]);
return 0;
}
习题:P7381 [COCI 2018/2019 #6] Sličice
问题分析
这个问题要求在给予 \(K\) 张照片后,计算能获得的最大总分数。一个关键的思路是,将问题分解为两部分:
- 计算出初始时(未获得新照片时)的总分数。
- 计算出这 \(K\) 张照片最多能带来多少额外的分数增长。
最终答案就是初始总分加上最大的额外分数。
计算“最大分数增长”的过程,是一个典型的分组背包问题。
- 背包容量:总共有 \(K\) 张新照片可以分配,所以背包的总容量是 \(K\)。
- 物品组:\(N\) 个球队,每个球队是一个物品组。
- 组内物品:对于第 \(i\) 个球队,可以选择给它分配 \(c\) 张照片,这个选择就是一个“物品”。
- 体积:给球队 \(i\) 分配 \(c\) 张照片,消耗的“体积”是 \(c\)。
- 价值:这个选择带来的分数增量是 \(B_{P_i + c} - B_{P_i}\)。
目标是在总体积不超过 \(K\) 的前提下,从每个组中最多选择一个物品,使得总价值(总分数增量)最大。
解题思路
使用 \(dp_j\) 表示总共分配了 \(j\) 张新照片的情况下,所能获得的最大分数增量。
目标是求解 \(dp_K\)。
依次遍历每个球队(物品组),对于每个球队 \(i\),更新 \(dp\) 数组。
如果压到一维数组的情况下,为了保证每个球队(组)只做一次决策(只选一个 \(c\)),需要倒序遍历背包容量 \(j\)。
对于每个容量 \(j\),再遍历所有可能的决策 \(c\)(即给当前球队 \(i\) 分配 \(c\) 张照片)。
- 价值:分配 \(c\) 张照片带来的分数增量为 \(B_{P_i + c} - B_{P_i}\)。
- 决策:在“不给当前球队分配这 \(c\) 张照片”和“分配”之间做选择。
- 如果不分配,最大增量保持为 \(dp_j\)(继承自上一个球队的状态)。
- 如果分配,则最大增量为 \(dp_{j-c} + B_{P_i + c} - B_{P_i}\)。这表示用 \(j-c\) 的容量取得了之前的最大增量,然后花费 \(c\) 的容量给当前球队,获得 \(B_{P_i + c} - B_{P_i}\) 的价值。
状态转移方程为:\(dp_j \leftarrow \max (dp_j, dp_{j-c} + (B_{P_i + c} - B_{P_i}))\)。
最终的最大总分等于初始的总分加上 \(dp_K\)。
该算法时间复杂度为 \(O(NK^2)\),满足题目要求。
参考代码
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 505;
int p[N]; // p[i]: 第 i 支球队已有的照片数量
int b[N]; // b[x]: 拥有 x 张照片能获得的分数
// dp[j]: 表示总共分配 j 张新照片的情况下,所能获得的“最大分数增量”
int dp[N];
int main()
{
int n, m, k;
// n: 球队数, m: 每队最大照片数, k: 可分配的新照片总数
scanf("%d%d%d", &n, &m, &k);
for (int i = 1; i <= n; i++) {
scanf("%d", &p[i]);
}
for (int i = 0; i <= m; i++) {
scanf("%d", &b[i]);
}
// 1. 计算初始总分
int initial_score = 0;
for (int i = 1; i <= n; i++) {
initial_score += b[p[i]];
}
// dp 数组全局初始化为0,代表花费0张照片,分数增量为0
// 2. 分组背包过程,计算最大分数增量
// 遍历每个球队 (物品组)
for (int i = 1; i <= n; i++) {
// 倒序遍历背包容量,保证每个组的决策只基于上一组的状态
for (int j = k; j >= 1; j--) {
// 遍历组内决策 (给当前球队分配 cnt 张照片)
// cnt 最小为1,因为 cnt=0 不产生分数增量,无需计算
// cnt 不能超过当前容量 j,也不能超过球队剩余空位数 m - p[i]
for (int cnt = 1; cnt <= min(j, m - p[i]); cnt++) {
// 计算价值:分数增量
int increase = b[p[i] + cnt] - b[p[i]];
// 状态转移:在“不分配”和“分配”中取最优
dp[j] = max(dp[j], dp[j - cnt] + increase);
}
}
}
// 3. 最终答案 = 初始总分 + K张照片带来的最大增量
printf("%d\n", initial_score + dp[k]);
return 0;
}
习题:P5365 [SNOI2017] 英雄联盟
有 \(N\) 个英雄,每个英雄 \(i\) 最多可以购买 \(K_i\) 款皮肤,每款皮肤价格为 \(C_i\)。购买 \(s_i \gt 0\) 款皮肤的英雄 \(i\),可以提供 \(s_i\) 种展示方案。总的展示方案数是所有已购买皮肤的英雄的方案数之积。如果一个英雄没有购买皮肤,则它对总方案数的贡献为 \(1\),求使得总展示方案数至少为 \(M\) 的最小花费。
解题思路
这是一个典型的动态规划问题,可以看做是分组背包问题的一个变种。要求的是达到目标方案数的最小花费,可以反过来思考:在一定的花费下,最多能获得多少种展示方案。
定义 \(dp_{i,j}\) 为只考虑前 \(i\) 个英雄,总花费恰好为 \(j\) 时,能够获得的最大展示方案数。
对于第 \(i\) 个英雄,可以选择为它购买 \(cnt\) 款皮肤,其中 \(0 \le cnt \le K_i\)。
- 花费:购买 \(cnt\) 款皮肤的花费是 \(cnt \times C_i\)。
- 前序状态:这笔花费 \(cnt \times C_i\) 用掉后,分配给前 \(i-1\) 个英雄的花费就是 \(j-cnt \times C_i\)。在此花费下,前 \(i-1\) 个英雄能产生的最大方案数是 \(dp_{i-1, j-cnt \times C_i}\)。
- 方案数计算:根据题意,购买 \(cnt\) 款皮肤,会使总方案数乘以 \(cnt\)。但特殊地,购买 \(0\) 款或 \(1\) 款皮肤,都只提供 \(1\) 种方案(不展示,或只有一种展示选择),对总方案数的乘积因子都是 \(1\)。因此,购买 \(cnt\) 款皮肤的贡献因子是 \(\max (cnt, 1)\)。
- 转移方程:需要遍历为第 \(i\) 个英雄购买皮肤的所有可能数量(从 \(0\) 到 \(K_i\)),并选择使得总方案数最大的一种。\(dp_{i,j} = \max \{ dp_{i-1, j - cnt \times C_i} \times \max(cnt,1) \}\),其中 \(0 \le cnt \le K_i\) 且 \(j \ge cnt \times C_i\)。
当 \(i=0\),即不考虑任何英雄时,无论花费多少,都只有 \(1\) 种方案(空方案),所以 \(dp_{0,j}=1\) 对所有 \(j \ge 0\) 成立。
观察转移方程可以发现,\(dp_i\) 的计算只依赖于 \(dp_{i-1}\)。因此,可以使用滚动数组来优化空间复杂度。
在计算 DP 的过程中,每当计算出一个值,就立刻检查它是否满足大于等于 \(M\)。如果满足,那么该状态的花费就是一个可能的答案,用它来更新全局的最小花费。
参考代码
#include <cstdio>
#include <algorithm>
using ll = long long;
using std::max;
using std::min;
const int N = 150;
const int C = 3e5 + 5;
int k[N], c[N];
// dp[i][j]: 只考虑前 i 个英雄,花费为 j 时的最大方案数
// 使用滚动数组优化空间,dp[0] 和 dp[1] 交替表示前 i-1 和前 i 个英雄的状态
ll dp[2][C];
int main()
{
int n; ll m; scanf("%d%lld", &n, &m);
int maxc = 0; // 计算理论上的最大总花费
for (int i = 1; i <= n; i++) scanf("%d", &k[i]);
for (int i = 1; i <= n; i++) {
scanf("%d", &c[i]);
maxc += k[i] * c[i];
}
int ans = maxc; // 初始化答案为最大花费,之后不断取最小值
// Base Case: i=0,不考虑任何英雄时,无论花费多少,方案数都为1(空方案)
for (int i = 0; i <= maxc; i++) dp[0][i] = 1;
// DP主循环,遍历每个英雄
for (int i = 1; i <= n; i++) {
int cur = i % 2, pre = 1 - cur; // 滚动数组下标
// 遍历所有可能的花费 j
for (int j = 0; j <= maxc; j++) {
// 初始化 dp[cur][j]
// 这一步等效于处理 cnt=0 的情况,即不给第i个英雄买皮肤
// dp[cur][j] = dp[pre][j] * max(0, 1) = dp[pre][j]
// 代码中直接设为1,然后在cnt=0的循环中会通过 max(1, dp[pre][j]) 修正为正确的值
dp[cur][j] = 1;
// 遍历为第 i 个英雄购买的皮肤数量 cnt
for (int cnt = 0; cnt <= k[i]; cnt++) {
// 确保花费 j 足够购买 cnt 个皮肤
if (j >= cnt * c[i])
// 状态转移方程
// 新方案数 = (前i-1个英雄在花费 j-cnt*c[i] 时的方案数) * (第i个英雄买cnt个皮肤的贡献)
// 购买 cnt 个皮肤的贡献因子为 max(cnt, 1)
dp[cur][j] = max(dp[cur][j], 1ll * dp[pre][j - cnt * c[i]] * max(cnt, 1));
}
// 每计算出一个状态,就检查是否满足 M 的要求,并更新最小花费 ans
if (dp[cur][j] >= m) ans = min(ans, j);
}
}
printf("%d\n", ans);
return 0;
}
习题:P5322 [BJOI2019] 排兵布阵
玩家小 C 有 \(m\) 名士兵,需要在 \(n\) 座城堡中进行部署,以对抗 \(s\) 名其他的玩家。对于所有的 \(s\) 场对战,小 C 的士兵部署方案必须完全相同。
在单场对战中,如果小 C 在第 \(i\) 座城堡部署的士兵数量严格大于对手的两倍,他就能占领该城堡并获得 \(i\) 分。
小 C 的总分是他与所有 \(s\) 名玩家对战后获得的分数之和。现在已知所有 \(s\) 名玩家的布阵策略(玩家 \(i\) 在城堡 \(j\) 的兵力数是 \(a_{i,j}\)),求出小 C 能获得的最大总分。
问题分析
此问题可以抽象为分组背包问题。
- 背包容量:总士兵数 \(m\)。
- 分组:\(n\) 座城堡,每座城堡是一个分组。
- 物品:对于城堡 \(i\)(第 \(i\) 个分组),有 \(s\) 个物品。第 \(j\) 个物品代表“战胜 \(j\) 个对手”这一策略。要战胜 \(j\) 个对手,需要投入的兵力必须超过这 \(j\) 个对手中兵力最多的人的两倍。因此,先将 \(s\) 个对手在城堡 \(i\) 的兵力从小到大排序。
- 物品重量:战胜 \(j\) 个对手所需的最少兵力。
- 物品价值:战胜 \(j\) 个对手的总得分 \(i \times j\)。
需要从每个分组(城堡)中至多选择一个物品(策略),使得总重量(总兵力)不超过背包容量 \(m\),且总价值(总得分)最大。
解题思路
设 \(dp_j\) 表示花费 \(j\) 个士兵(背包容量为 \(j\))时,能获得的最大分数。这是一个经过空间优化的状态,省略了代表“前 \(i\) 个分组”的维度。
遍历每个分组,对于每个分组,更新 \(dp\) 数组。为了确保在处理分组 \(i\) 时,所依赖的 \(dp\) 值是来自处理完分组 \(i-1\) 后的状态,需要对背包容量(士兵数 \(j\))进行逆序遍历。
对于城堡 \(i\) 中的每个策略 \(k\)(战胜 \(k\) 个对手),设 \(c\) 是此时需要分配的士兵数,也就是排序后的第 \(k\) 项士兵数的两倍加一,则 \(dp_j = \max(dp_j, \ dp_{j-c} + k \times i)\)。
通过逆序遍历 \(j\),当计算 \(dp_j\) 时,\(dp_{j-c}\) 存储的还是处理分组 \(i-1\) 时的旧值,这等价于二维 DP 中的 \(dp_{i-1,j-c}\),从而保证了每个分组的策略只会被选择一次。
时间复杂度:\(O(ns(m + \log s))\)。对于 \(n\) 座城堡,每座城堡的 DP 更新需要两层循环,遍历容量 \(m\) 和组内物品 \(s\),另外还有对 \(s\) 个对手的士兵分配数的排序。
参考代码
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 105;
const int M = 20005;
const int INF = 1e9;
const int B = 510000;
int a[N][N], dp[M], tmp[N];
int main()
{
int s, n, m;
scanf("%d%d%d", &s, &n, &m);
for (int i = 1; i <= s; i++)
for (int j = 1; j <= n; j++)
scanf("%d", &a[i][j]);
int ans = 0;
// 外层循环:遍历n座城堡,每座城堡是一个分组
for (int i = 1; i <= n; i++) {
// 提取当前城堡i的所有对手兵力
for (int j = 1; j <= s; j++) tmp[j] = a[j][i];
// 排序,以确定击败1, 2, ..., s个对手分别需要的成本
sort(tmp + 1, tmp + s + 1);
// 核心DP:分组背包,空间优化为一维
for (int j = m; j >= 0; j--) {
// 遍历组内物品k(代表击败k个对手的策略)
for (int k = 1; k <= s; k++) {
int cost = 2 * tmp[k] + 1;
if (j < cost) break; // 如果当前容量连此成本都付不起,后续更大成本更不可能
int value = k * i;
// 状态转移
dp[j] = max(dp[j], dp[j - cost] + value);
ans = max(ans, dp[j]);
}
}
}
printf("%d\n", ans);
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号