树的直径

树的直径是指树上最远的两点间的距离，又称为树的最远点对。有两种方法求树的直径，时间复杂度都为 \(O(n)\)：

做两次 DFS（或 BFS）
树形 DP

两种方法有各自的优点和缺点。

做两次 DFS（或 BFS）方法的优点是能得到完整的路径。因为它用搜索的原理，从起点 \(u\) 出发一步一步求 \(u\) 到其他所有点的距离，能记录路径经过了哪些点。缺点是不能用于有负权边的树。

树形 DP 方法的优点是允许树上有负权边。缺点是只能求直径的长度，无法得到这条直径的完整路径。

例题：PT07Z - Longest path in a tree

做两次 DFS（或 BFS）

当边权没有负值时，计算树的直径可以通过做两次搜索遍历解决，步骤如下：

从树上的任意点 \(r\) 出发，求距离它最远的点 \(s\)，则 \(s\) 肯定是直径的两个端点之一。
从 \(s\) 出发，求距离 \(s\) 最远的点 \(t\)，则 \(t\) 是直径的另一个端点。

因此 \(s\) 和 \(t\) 就是距离最远的两个点，即树的直径的两个端点。

证明

使用反证法，假设 \(x\) 到 \(y\) 才是真正的直径，而第一次遍历找到的距离 \(r\) 最远的点 \(s\) 不为 \(x\) 或 \(y\)。

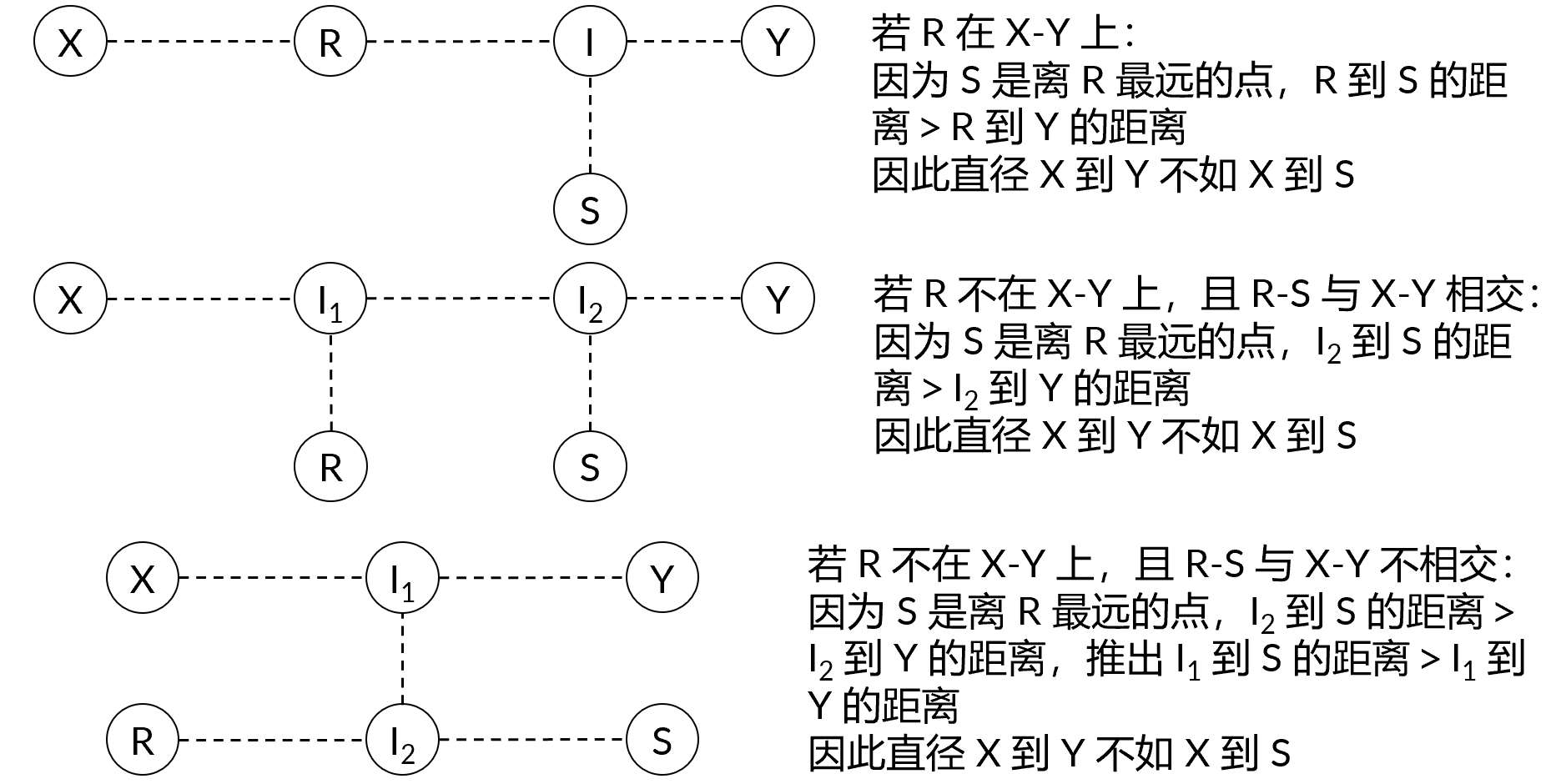
这个例子说明，以贪心原理进行路径长度搜索，当树上有负权边时，只能获得局部最优，而无法获得全局最优，这与图论中的 Dijkstra 算法不能用于负权边是同样的道理。

#include <cstdio>
#include <vector>
using namespace std;
const int N = 10005;
vector<int> tree[N];
int dis[N]; // 记录距离
void dfs(int u, int fa) {
    for (int v : tree[u]) {
        if (v == fa) continue;
        dis[v] = dis[u] + 1;
        dfs(v, u);
    }
}
int main()
{
    int n;
    scanf("%d", &n);
    for (int i = 1; i < n; i++) {
        int u, v;
        scanf("%d%d", &u, &v);
        tree[u].push_back(v); tree[v].push_back(u);
    }   
    dfs(1, 0); // 任选一个起点（如1）计算到树上每个节点的距离
    int s = 0;
    for (int i = 1; i <= n; i++) 
        if (dis[i] > dis[s]) s = i; // 找最远的点s，s是直径的一个端点
    dis[s] = 0;
    dfs(s, 0); // 从s出发，计算以s为起点，到树上每个节点的距离
    int ans = 0;
    for (int i = 1; i <= n; i++) ans = max(ans, dis[i]);
    printf("%d\n", ans);
    return 0;
}

树形 DP

定义状态 \(dp_u\) 表示以 \(u\) 为根节点的子树上，从 \(u\) 出发能到达的最远路径长度，这个路径的终点是 \(u\) 的一个叶子节点。

状态转移：\(dp_u = \max \{ dp_{v} + edge(u,v) \}, \ v \in son_u\)

整棵树的直径怎么求？设 \(f_u\) 代表经过点 \(u\) 的最长路径长度，显然，在所有的 \(f_u\) 中，最大值就是树的直径长度。

如何计算 \(f_u\) ？实际上在 \(dp_u\) 的计算过程中相当于尝试每一棵子树的贡献，而经过 \(u\) 的最长路径实际上可以用最优的两棵子树合并得到，因此只需在枚举子节点计算 \(dp_u\) 时记录最大值和次大值，最大值加次大值即为 \(f_u\) 的结果。

#include <cstdio>
#include <vector>
using namespace std;
const int N = 10005;
vector<int> tree[N];
int dp[N], ans;
void dfs(int u, int fa) {
    int max1 = 0, max2 = 0;
    for (int v : tree[u]) {
        if (v == fa) continue;
        dfs(v, u);
        if (dp[v] + 1 > max1) {
            max2 = max1;
            max1 = dp[v] + 1;
        } else if (dp[v] + 1 > max2) {
            max2 = dp[v] + 1;
        }
    }
    dp[u] = max1;
    ans = max(ans, max1 + max2);
}
int main()
{
    int n;
    scanf("%d", &n);
    for (int i = 1; i < n; i++) {
        int u, v;
        scanf("%d%d", &u, &v);
        tree[u].push_back(v); tree[v].push_back(u);
    }
    dfs(1, 0);
    printf("%d\n", ans);
    return 0;
}

习题：P3174 [HAOI2009] 毛毛虫

解题思路

本题要求的最大“毛毛虫”实际上是在树的直径的基础上多了一些“脚”，可以借用求直径的思路。

定义状态 \(dp_u\) 表示以 \(u\) 为根节点的子树上，\(u\) 到某个叶子节点形成的最大“身体+脚”的个数，则有状态转移：\(dp_u = \max \{ dp_v + 1 \} + feet\)，这里的 \(feet\) 代表“脚”的数量，当 \(u\) 没有子树时，就没有额外的“脚”，有子树时，除了作为主干身体的那一枝以外，其他的子树可以留一个点做“脚”。

类似求直径的方法，此时经过点 \(u\) 的最大“毛毛虫”可以基于计算 \(dp_u\) 过程中最大和次大的两次计算来提供毛毛虫的“身体”，则 \(u\) 的其他邻居节点可以提供“脚”。注意这里计算的“脚”的数量要考虑 \(u\) 的父节点。

参考代码

#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
const int N = 300005;
vector<int> tree[N];
int dp[N], ans;
void dfs(int u, int fa) {
    int child = 0;
    int max1 = 0, max2 = 0;
    for (int v : tree[u]) {
        if (v == fa) continue;
        child++;
        dfs(v, u);
        if (dp[v] > max1) {
            max2 = max1; max1 = dp[v]; 
        } else if (dp[v] > max2) {
            max2 = dp[v];
        }
    }
    dp[u] = max1 + 1 + max(child - 1, 0);
    ans = max(ans, max1 + max2 + 1 + max(child - 2, 0) + (fa != 0));
}
int main()
{
    int n, m; scanf("%d%d", &n, &m);
    while (m--) {
        int a, b; scanf("%d%d", &a, &b);
        tree[a].push_back(b); tree[b].push_back(a); 
    }
    dfs(1, 0);
    printf("%d\n", ans);
    return 0;
}

例题：P5021 [NOIP2018 提高组] 赛道修建

分析：对于 \(m=1\) 的情况，求树的直径即可。

对于链的情况，就是一个经典分段问题，让每段的和的最小值最大的问题，二分答案 + 贪心。

对于菊花树的情况，当 \(2m \lt n\) 时，拿最大的 \(2m\) 条边最大、最小搭配；\(2m \ge n\) 时，可以先补若干个 \(0\)，再进行最大最小搭配，搭配上 \(0\) 相当于自己成一条赛道。

参考代码

#include <cstdio>
#include <vector>
#include <utility>
#include <algorithm>
using std::vector;
using std::pair;
using std::max;
using std::min;
using std::sort;
using edge = pair<int, int>; // node, weight
const int N = 50005;
vector<edge> tree[N];
int n, m, dp[N], diam, arr[N], idx;
bool check_chain() {
    for (int i = 1; i <= n; i++)
        if (tree[i].size() > 2) return false;
    return true;
}
void dfs_diameter(int u, int fa) {
    for (edge e : tree[u]) {
        int v = e.first, w = e.second;
        if (v == fa) continue;
        dfs_diameter(v, u);
        diam = max(diam, dp[u] + dp[v] + w);
        dp[u] = max(dp[u], dp[v] + w);
    }
}
void build_chain(int u, int fa) {
    for (edge e : tree[u]) {
        int v = e.first, w = e.second;
        if (v == fa) continue;
        arr[++idx] = w;
        build_chain(v, u);
    }
}
bool check(int x) {
    int cnt = 0, sum = 0;
    for (int i = 1; i < n; i++) {
        if (sum + arr[i] >= x) {
            cnt++; sum = 0;
        } else sum += arr[i];
    }
    return cnt >= m;
} 
bool check_flower() {
    return tree[1].size() == n - 1;
}
int main()
{
    scanf("%d%d", &n, &m);
    int sum = 0;
    for (int i = 1; i < n; i++) {
        int a, b, l; scanf("%d%d%d", &a, &b, &l);
        tree[a].push_back({b, l});
        tree[b].push_back({a, l});
        sum += l;
        arr[i] = l;
    }
    if (m == 1) {
        dfs_diameter(1, 0);
        printf("%d\n", diam); 
    } else if (check_chain()) {
        build_chain(1, 0);
        int l = 1, r = sum / m, ans = 1;
        while (l <= r) {
            int mid = (l + r) / 2;
            if (check(mid)) {
                l = mid + 1; ans = mid;
            } else {
                r = mid - 1;
            }
        }
        printf("%d\n", ans);
    } else if (check_flower()) {
        if (2 * m >= n) {
            for (int i = n; i <= 2 * m; i++) arr[i] = 0;
            sort(arr + 1, arr + 2 * m + 1, [](int lhs, int rhs) {
                return lhs > rhs;
            });
        } else {
            sort(arr + 1, arr + n, [](int lhs, int rhs) {
                return lhs > rhs;
            }); 
        }
        int ans = sum;
        for (int i = 1; i <= m; i++) ans = min(ans, arr[i] + arr[2 * m - i + 1]);
        printf("%d\n", ans);
    }
    return 0;
}

对于一般情况，最小值最大化问题想到二分答案 \(x\)。

对于树上问题，考虑 DFS 并回溯，从下往上一层一层处理，对于每一个点会为它的父亲提供一条链，对于一个点，它儿子提供的链中加上它向它儿子的这条边的长度 \(\ge x\) 的可以直接成一条赛道，否则应该等待和其他儿子的拼接。

最优拼接策略也是一个经典贪心问题，从小到大看每条链，每次处理最短的链（设其长度为 \(b\)），则相当于要找到 \(\ge x - b\) 的最短链，配对成一条赛道，这个过程可以借助 multiset 实现，最后将剩余的没构成赛道的最长的链向上传递。

DFS 完成后看是否能够形成 \(\ge m\) 条赛道，来判断 \(x\) 是否可行，整体时间复杂度为 \(O(n \log n \log \dfrac{\sum l_i}{m})\)。

参考代码

#include <cstdio>
#include <utility>
#include <vector>
#include <set>
using std::vector;
using std::multiset;
using std::pair;
using edge = pair<int, int>; // node, weight
const int N = 50005;
vector<edge> tree[N];
int n, m, cnt, len[N];
void dfs(int u, int fa, int x) {
    multiset<int> s;
    for (edge e : tree[u]) {
        int v = e.first, w = e.second;
        if (v == fa) continue;
        dfs(v, u, x);
        if (len[v] + w >= x) cnt++;
        else s.insert(len[v] + w);
    }
    len[u] = 0;
    while (!s.empty()) {
        int b = *s.begin();
        s.erase(s.begin());
        int y = x - b;
        auto iter = s.lower_bound(y);
        if (iter != s.end()) {
            s.erase(iter); cnt++;
        } else {
            len[u] = b;
        }
    }
}
bool check(int x) {
    cnt = 0;
    dfs(1, 0, x);
    return cnt >= m;
}
int main()
{
    scanf("%d%d", &n, &m);
    int sum = 0;
    for (int i = 1; i < n; i++) {
        int a, b, l; scanf("%d%d%d", &a, &b, &l);
        tree[a].push_back({b, l});
        tree[b].push_back({a, l});
        sum += l;
    }
    int l = 1, r = sum / m, ans = 1;
    while (l <= r) {
        int mid = (l + r) / 2;
        if (check(mid)) {
            l = mid + 1; ans = mid;
        } else {
            r = mid - 1;
        }
    }
    printf("%d\n", ans);
    return 0;
}

习题：P4271 [USACO18FEB] New Barns P

解题思路

首先，按照题意，这里的连通块必然是一棵树。

对于询问操作，先考虑如果查询是给定一对 \(k_1\) 和 \(k_2\) 求距离，那么常见的计算方式是 \(d_{k_1} + d_{k_2} - 2 \times d_{lca}\)。

这里新建一个节点的操作并不会影响其他节点的深度，而求 LCA 需要的 \(fa\) 数组也只有涉及到新增节点的部分需要修改，因此时间复杂度是 \(O(\log q)\) 的。

那么到这里问题变成了对于一棵树和其中给定的一个 \(k\)，离它最远的点是谁？

一定会是直径两个端点中的一个。

因此，需要动态维护每个连通块的直径端点。当新增的是一个独立的点时，则该连通块的直径就是该点本身。当新增的是一个与某个现有的点相连的点时，则新的连通块的直径要么是原来的直径，要么是新增的这个点与原来的两个直径端点之间的路径，对三种情况比较更新即可。

参考代码

#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 100005;
const int LOG = 17;
char op[5];
int depth[N], root[N], fa[N][LOG], diam[N][3];
// diam[][0/1] 直径的两个端点   diam[][2] 直径大小
int lca(int x, int y) {
    if (depth[x] < depth[y]) swap(x, y);
    int delta = depth[x] - depth[y];
    for (int i = 0; i < LOG; i++) {
        if (delta & 1) x = fa[x][i];
        delta >>= 1;
    }
    if (x == y) return x;
    for (int i = LOG - 1; i >= 0; i--)
        if (fa[x][i] != fa[y][i]) {
            x = fa[x][i]; y = fa[y][i];
        }
    return fa[x][0];
}
int main()
{
    int q; scanf("%d", &q);
    int id = 0;
    while (q--) {
        int p; scanf("%s%d", op, &p);
        if (op[0] == 'B') {
            id++; 
            if (p == -1) {
                root[id] = id; diam[id][0] = diam[id][1] = id;
            } else {
                fa[id][0] = p; depth[id] = depth[p] + 1;
                for (int i = 1; i < LOG; i++) fa[id][i] = fa[fa[id][i - 1]][i - 1];
                int r = root[p]; root[id] = r;
                int p1 = diam[r][0], p2 = diam[r][1];
                int lca1 = lca(p1, id), lca2 = lca(p2, id);
                int dis1 = depth[id] + depth[p1] - 2 * depth[lca1];
                int dis2 = depth[id] + depth[p2] - 2 * depth[lca2];
                if (dis1 > dis2 && dis1 > diam[r][2]) {
                    diam[r][2] = dis1; diam[r][1] = id;
                } else if (dis2 > diam[r][2]) {
                    diam[r][2] = dis2; diam[r][0] = id;
                }
            }
        } else {
            int r = root[p], p1 = diam[r][0], p2 = diam[r][1];
            int dis1 = depth[p] + depth[p1] - 2 * depth[lca(p, p1)];
            int dis2 = depth[p] + depth[p2] - 2 * depth[lca(p, p2)];
            printf("%d\n", max(dis1, dis2));
        }
    }
    return 0;
}

posted @ 2024-05-12 12:02 RonChen 阅读(215) 评论(0) 收藏举报

刷新页面返回顶部

RonChen

树的直径

例题：PT07Z - Longest path in a tree

做两次 DFS（或 BFS）

树形 DP

习题：P3174 [HAOI2009] 毛毛虫

例题：P5021 [NOIP2018 提高组] 赛道修建

习题：P4271 [USACO18FEB] New Barns P

公告