DAG与拓扑排序
现实生活中我们经常要做一连串事情，这些事情之间有顺序关系或依赖关系，做一件事情之前必须先做另一件事，如安排客人的座位、穿衣服的先后、课程学习的先后等。这些事情可以抽象为图论中的拓扑排序（Topological Sorting）问题。
给定一张有向无环图（在有向图中，从一个节点出发，最终回到它自身的路径被称为“环”，不存在环的有向图即为有向无环图），若一个由图中所有点构成的序列 \(A\) 满足：对于图中的每条边 \((x,y)\)，\(x\) 在 \(A\) 中都出现在 \(y\) 之前，则称 \(A\) 是该有向无环图顶点的一个拓扑序。求解序列 \(A\) 的过程就称为拓扑排序。
显然，一个图的拓扑序不一定唯一。
另外，只有在有向无环图（DAG）中才有拓扑序，如果图中有环，则没有合法的拓扑序。
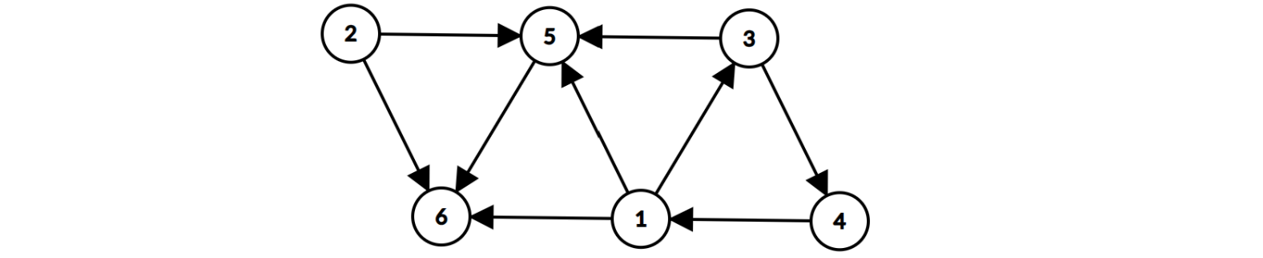
选择题：如图是一张包含 6 个顶点的有向图，但顶点间不存在拓扑序。如果要删除其中一条边，使这 6 个顶点能进行拓扑排序，请问总共有多少条边可以作为候选的被删除边？
- A. 1
- B. 2
- C. 3
- D. 4
答案
之所以不存在拓扑序，是因为图中目前有 1 -> 3 -> 4 -> 1 这个环。把这个环中的任意一条边去掉则这个图可以进行拓扑排序，答案选 C。
例题：B3644 【模板】拓扑排序 / 家谱树
给定一个家族中 \(N\) 个人的后代关系，要求输出一个所有人的排列序列，使得在这个序列中，任何一个长辈都出现在其所有后辈的前面。
这个问题本质上是要求根据一系列的“先后”约束条件，对所有元素进行排序。具体来说，如果 \(j\) 是 \(i\) 的后代，那么 \(i\) 必须排在 \(j\) 的前面，这是一个典型的拓扑排序问题。
可以将这个问题模型化为一个有向图：
- 每个人是图上的一个顶点。
- 如果 \(j\) 是 \(i\) 的后代，就建立一条从 \(i\) 到 \(j\) 的有向边，记为 \(i \rightarrow j\)。这条边表示 \(i\) 必须在 \(j\) 之前被处理。
这样，整个家族关系就构成了一个有向无环图。家谱关系中不会出现“自己是自己的祖先”这样的循环，所以图一定是无环的。
目标就是求出这个图的一个拓扑序列，拓扑序列是一个顶点的线性排列，它使得对于图中任意一条边 \(u \rightarrow v\)，\(u\) 在序列中都出现在 \(v\) 之前。
解决拓扑排序的经典算法是卡恩（Kahn）算法，该算法基于广度优先搜索（BFS），思路清晰，易于实现。
Kahn 算法的核心思想是：不断地从图中移除入度为 0 的顶点，并将这些顶点加入到拓扑排序的结果序列中。
算法从所有入度为 0 的顶点开始，将它们假如排序结果。然后，将这些顶点从图中“移除”（逻辑上），这意味着它们指向的那些顶点的入度都需要减 1。如果此时出现了新的入度为 0 的顶点，就将它们加入一个队列中，等待处理。重复这个过程，直到所有顶点都被处理。
参考代码
#include <cstdio>
#include <vector>
#include <queue>
using namespace std;
const int N = 105;
vector<int> graph[N]; // 邻接表存图
int ind[N]; // 存储每个顶点的入度
int ans[N]; // 存储拓扑排序的结果
int main()
{
int n; scanf("%d", &n);
// 1. 建图并统计每个顶点的入度
for (int i = 1; i <= n; i++) {
while (true) {
int x; scanf("%d", &x);
if (x == 0) break;
// i 是 x 的长辈，所以有一条从 i 到 x 的有向边
graph[i].push_back(x);
ind[x]++; // x 的入度加1
}
}
// 2. 初始化队列，将所有入度为0的顶点入队
queue<int> q;
for (int i = 1; i <= n; i++) {
if (ind[i] == 0) {
q.push(i);
}
}
// 3. Kahn算法主循环
int idx = 0; // 结果数组的索引
while (!q.empty()) {
// a. 从队列中取出一个入度为0的顶点
int u = q.front(); q.pop();
// b. 将该顶点加入结果序列
idx++; ans[idx] = u;
// c. 遍历该顶点的所有邻接点
for (int v : graph[u]) {
// d. 将邻接点的入度减1
ind[v]--;
// e. 如果邻接点入度变为0，则将其入队
if (ind[v] == 0) {
q.push(v);
}
}
}
// 4. 输出结果
for (int i = 1; i <= idx; i++) {
printf("%d%c", ans[i], i == idx ? '\n' : ' ');
}
return 0;
}
例题：P4017 最大食物链计数
给出一个食物网，要求出这个食物网中最大食物链的数量。这里的“最大食物链”，指的是生物学意义上的食物链，即开头是不会捕食其他生物的生产者，结尾是不会被其他生物捕食的消费者。答案可能很大，所以要对 \(80112002\) 取模。
分析： 考虑把这个食物网转换为一个图，食物网有什么样的特点呢？
- 食物网中的捕食关系一定是单向的（比如猫吃鱼，而不是鱼吃猫）。
- 食物网中的捕食关系一定是无环的，不存在 A 捕食 B，B 捕食 C，C 捕食 A 这种情况。
所以可以发现食物网其实就是一个 DAG（有向无环图）。在这道题目中“最大食物链”的定义就是一条从入度为 \(0\) 的点开始到出度为 \(0\) 的点结束的链，即要计算这样的链的个数。
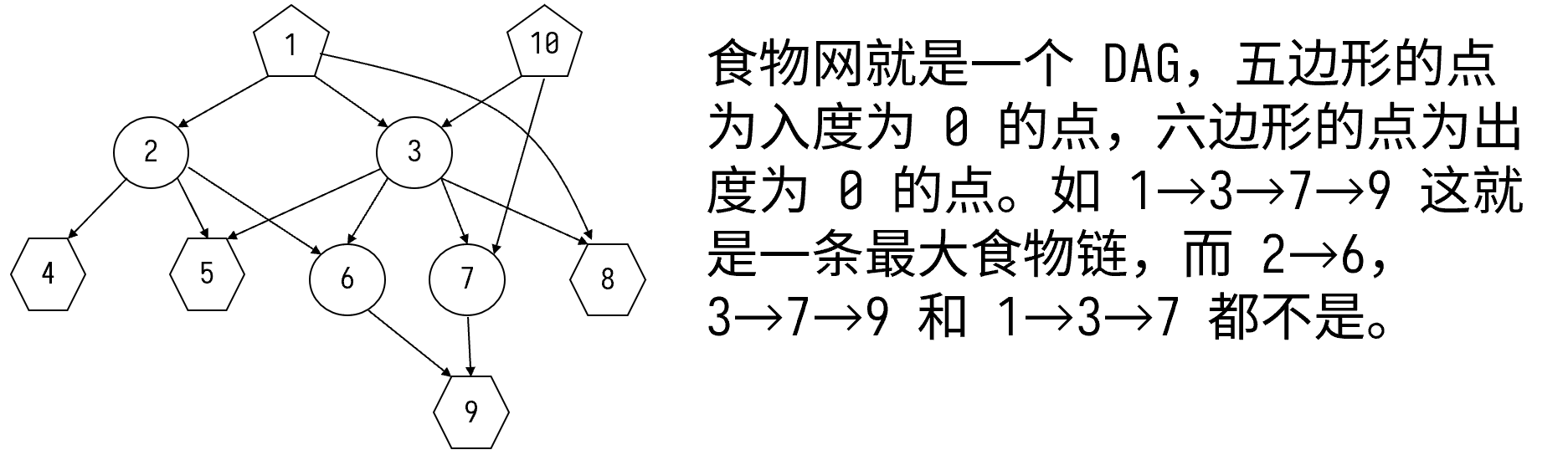
用一个数组 f[x] 表示从任意一个入度为 0 的点到点 x 的食物链计数。那么对于任意一个入度为 0 的点 y，它的 f[y]=1。对于一个入度非 0 的点 z，它的 f[z] 等于能到达点 z 的点 u 的 f[u] 之和。
如点 3，它的食物链计数等于点 1 的食物链计数加上点 10 的，即 f[3]=f[1]+f[10]=1+1=2。而对于点 6，它的食物链计数等于点 2 的食物链计数加上点 3 的，即 f[6]=f[2]+f[3]=1+2=3。这样最后只要对所有出度为 0 的点的事物链计数求和就能求出题目所求的答案了。
在计算 f[x] 的过程中，需要保证对于点 x，所有能到达点 x 的点 y 的 f[y] 已经被计算过了，这样就需要确定一个合适的计算顺序。因此使用 拓扑排序 来控制计算顺序。拓扑排序并不是对一个数列进行排序，而是在 DAG 上对点进行排序，使得在搜到点 x 时所有能到达点 x 的点 y 的结果已经计算完成了。具体流程如下：
- 统计每个点的入度，将所有入度为 0 的点加入处理队列。
- 将处于队头的点 x 取出，遍历点 x 能到达的所有点 y。
- 对于每一个 y，删去从点 x 到点 y 的边。在具体的实现中，只需要让 y 的入度减一即可。在这一步中，顺便可以对点 y 的数据进行维护，在这题中是
f[y]=(f[y]+f[x])%MOD。 - 如果点 y 的入度减到 0 了，说明所有能到 y 的点都被计算过了，这时将点 y 加入处理队列。
- 重复步骤 2 直到处理队列为空。
这样，就保证了在食物链计数这题中求 f[x] 的顺序正确。时间复杂度为 \(O(n+m)\)。
参考代码
#include <cstdio>
#include <vector>
#include <queue>
using namespace std;
const int N = 5005;
const int MOD = 80112002;
vector<int> graph[N];
int ind[N], f[N];
int main()
{
int n, m; scanf("%d%d", &n, &m);
for (int i = 1; i <= m; i++) {
int a, b; scanf("%d%d", &a, &b);
graph[a].push_back(b); // 存边
ind[b]++; // 点b的入度+1
}
queue<int> q;
for (int i = 1; i <= n; i++)
if (ind[i] == 0) {
q.push(i); f[i] = 1; // 将入度为0的点加入队列
}
while (!q.empty()) {
int u = q.front(); q.pop();
for (int v : graph[u]) {
f[v] = (f[v] + f[u]) % MOD;
ind[v]--;
if (ind[v] == 0) q.push(v); // 此时点y的依赖都解除了，将点y加入队列
}
}
int ans = 0;
for (int i = 1; i <= n; i++)
if (graph[i].size() == 0) ans = (ans + f[i]) % MOD;
printf("%d\n", ans);
return 0;
}
答案需要对 80112002 取模，在计算 f 时一边加一边取模，以及在对出度为 0 的点的食物链计数求和时一边加一边取模。如果只在输出答案时取模，那么可能在累加的过程中答案超出了数据类型存储的范围而导致答案的错误。
如果原图中有环，则拓扑排序过程中取出的点的数量会小于整个图的点数，有一些点的入度没有降到 \(0\)。
选择题：有如下的有向图，节点为 A,B,...,J，其中每条边的长度都标在图中。则节点 A 到节点 J 的最短路径长度为？
- A. 16
- B. 19
- C. 20
- D. 22
答案
B。
这是一个典型的有向无环图（DAG）的最短路径问题。
定义 \(d(X)\) 为从起点 A 到节点 X 的最短路径长度，目标是求 \(d(J)\)。
初始化 \(d(A) = 0\)。
计算第一层节点 B,C,D 的最短路径
- \(d(B) = d(A) + 2 = 2\)
- \(d(C) = d(A) + 5 = 5\)
- \(d(D) = d(A) + 1 = 1\)
计算第二层节点 E,F,G 的最短路径
- \(d(E) = \min (d(B)+12, d(C)+6, d(D)+13) = \min (2+12, 5+6, 1+13) = \min(14,11,14) = 11\)
- \(d(F) = \min(d(B)+10,d(C)+10)=\min(2+10,5+10)=\min(12,15)=12\)
- \(d(G) = \min(d(B)+14, d(C)+4, d(D)+11) = \min(2+14, 5+4, 1+11) = \min(16, 9, 12) = 9\)
计算第三层节点 H,I 的最短路径
- \(d(H) = \min(d(E)+3, d(F)+6, d(G)+8) = \min(11+3, 12+6, 9+8) = \min(14, 18, 17) = 14\)
- \(d(I) = \min(d(E)+9, d(F)+5, d(G)+10) = \min(11+9, 12+5, 9+10) = \min(20, 17, 19) = 17\)
计算终点 J 的最短路径：\(d(J) = \min(d(H)+5, d(I)+2) = \min(14+5, 17+2) = \min(19, 19) = 19\)
例题：P6145 [USACO20FEB] Timeline G
分析：\(s_i\) 为第 \(i\) 次挤奶最早开始的时间，初始值为输入。
在拓扑排序的过程中，设目前考虑的是点 \(u\)，它有一条指向 \(v\) 的边，则 \(s_v = \max (s_v, s_u + w(u, v))\)。
参考代码
#include <cstdio>
#include <utility>
#include <vector>
#include <queue>
#include <algorithm>
using std::vector;
using std::pair;
using std::queue;
using std::max;
using ll = long long;
using edge = pair<int, int>;
const int N = 100005;
ll s[N];
int ind[N];
vector<edge> graph[N];
int main()
{
int n, m, c; scanf("%d%d%d", &n, &m, &c);
for (int i = 1; i <= n; i++) scanf("%lld", &s[i]);
for (int i = 1; i <= c; i++) {
int a, b, x; scanf("%d%d%d", &a, &b, &x);
graph[a].push_back({b, x}); ind[b]++;
}
queue<int> q;
for (int i = 1; i <= n; i++) if (ind[i] == 0) q.push(i);
while (!q.empty()) {
int u = q.front(); q.pop();
for (edge e : graph[u]) {
int v = e.first, w = e.second;
s[v] = max(s[v], s[u] + w);
ind[v]--;
if (ind[v] == 0) q.push(v);
}
}
for (int i = 1; i <= n; i++) printf("%lld\n", s[i]);
return 0;
}
例题：P10480 可达性统计
给定一个 \(N\) 个点 \(M\) 条边的有向无环图，分别统计从每个点出发能够到达的点的数量。\(N,M \le 30000\)。
分析：设从点 \(x\) 出发能够到达的点构成的集合是 \(f(x)\)，则显然有：\(f(x) = \{ x \} \cup \left( \bigcup \limits_{存在有向边(x,y)} f(y) \right)\)。
也就是说，从 \(x\) 出发能够到达的点，是从“\(x\) 的各个后继节点 \(y\)”出发能够到达的点的并集，再加上点 \(x\) 自身。所以，在计算出一个点的所有后继节点的连通集合之后，就可以计算出该点的连通集合。因此可以用反向边建图，则这个图上的拓扑序是可以用来依次计算连通集合。
这里涉及到集合运算，结合 \(N \le 30000\)，可以使用 STL 中的 bitset 支持集合相关的高效运算。最终时间复杂度为 \(O\left(\dfrac{N(N+M)}{\omega}\right)\)，空间复杂度为 \(O\left(\dfrac{N^2}{\omega} + N + M\right)\)。
参考代码
#include <cstdio>
#include <vector>
#include <queue>
#include <bitset>
using std::vector;
using std::queue;
using std::bitset;
const int N = 30005;
vector<int> graph[N];
int ind[N];
bitset<N> ans[N];
int main()
{
int n, m; scanf("%d%d", &n, &m);
for (int i = 1; i <= m; i++) {
int x, y; scanf("%d%d", &x, &y);
graph[y].push_back(x);
ind[x]++;
}
queue<int> q;
for (int i = 1; i <= n; i++) {
if (ind[i] == 0) q.push(i);
ans[i][i] = 1;
}
while (!q.empty()) {
int u = q.front(); q.pop();
for (int v : graph[u]) {
ans[v] |= ans[u];
ind[v]--;
if (ind[v] == 0) q.push(v);
}
}
for (int i = 1; i <= n; i++) printf("%d\n", (int)ans[i].count());
return 0;
}
习题：AT_dp_g Longest Path
解题思路
设 \(dp_i\) 表示到 \(i\) 为止经过的最长路长度，\(dp_i = \max \{ dp_j + 1 \}\)，其中 \(j\) 为存在 \(j \rightarrow i\) 这样的边的点，可以在拓扑排序过程中求解。
参考代码
#include <cstdio>
#include <vector>
#include <queue>
using std::vector;
using std::queue;
using std::max;
int main()
{
int n, m; scanf("%d%d", &n, &m);
vector<vector<int>> g(n + 1);
vector<int> ind(n + 1), dp(n + 1);
for (int i = 1; i <= m; i++) {
int x, y; scanf("%d%d", &x, &y);
g[x].push_back(y); ind[y]++;
}
queue<int> q;
for (int i = 1; i <= n; i++) if (ind[i] == 0) q.push(i);
int ans = 0;
while (!q.empty()) {
int u = q.front(); q.pop();
for (int v : g[u]) {
dp[v] = max(dp[v], dp[u] + 1);
ans = max(ans, dp[v]);
ind[v]--;
if (ind[v] == 0) q.push(v);
}
}
printf("%d\n", ans);
return 0;
}
习题：P1807 最长路
在一个有向无环图（DAG）中，计算从 1 号顶点到 n 号顶点的最长路径长度。如果 1 号点无法到达 n 号点，输出 -1。
问题分析
要求从源点 1 到各点的最长路，设 \(dis_i\) 表示从 1 到 \(i\) 的最长路径长度。
如果已经知道了从 1 到 \(u\) 的最长路 \(dis_u\)，并且图中有一条边 \(u \rightarrow v\)，权重为 \(w\)，那么就有可能通过 \(u\) 到达 \(v\)，形成一条长度为 \(dis_u + w\) 的路径，可以用这个值来更新 \(dis_v\)。因为是求最长路，所以状态转移方程为 \(dis_v = \max (dis_v, \ dis_u + w)\)。
为了保证在计算 \(dis_v\) 时，\(dis_u\) 已经是一个最终的最优值，需要按照一定的顺序来处理图中的顶点。这个顺序就是拓扑序，在拓扑序列中，所有的前驱节点都排在后继节点的前面，很好地满足了 DP 的要求。
解题思路
标准的拓扑排序需要从所有入度为 0 的点开始，但本题只关心从 1 号点出发的路径。为了避免图中其他入度为 0 的点（例如点 \(k\)）对计算产生干扰（比如错误地计算了从 \(k\) 出发的最长路），首先进行一轮预处理。
正常建立图，并计算所有点的初始入度。进行一次特殊的拓扑排序，起始点是除了 1 号点以外所有入度为 0 的点。在这个排序过程中，只做一件事：将遍历到的顶点的邻接点的入度减 1，不进行任何距离计算。
这一轮结束后，所有与 1 号点无关的路径都被“模拟”走了一遍。此时，各顶点的入度值 \(ind_i\) 实际代表了“在只考虑从 1 号点出发的路径时，顶点 \(i\) 还有多少个未被访问的前驱”。
在经过预处理的图上，精确计算从 1 号点出发的最长路。
将 \(dis\) 数组（除 \(dis_1\)）初始化为负无穷，\(dis_1\) 作为源点，其值为 0。创建一个新队列，只将源点 1 放入。开始一次标准的基于拓扑排序的 DP，从队列中取出顶点 \(u\)，用 \(dis_u\) 更新其所有邻居 \(v\) 的最长距离，然后将 \(v\) 的入度减 1。若 \(v\) 的入度变为 0，则将其入队。
这一轮结束后，\(dis_n\) 中存储的就是从 1 到 n 的最长路径。如果其值仍为负无穷，则说明无法到达，输出 -1。
参考代码
#include <cstdio>
#include <vector>
#include <utility>
#include <queue>
using namespace std;
using pi = pair<int, int>;
const int N = 1505;
const int INF = 1e9;
vector<pi> g[N];
int dis[N], ind[N];
int main()
{
int n, m; scanf("%d%d", &n, &m);
// 正常建图，并计算初始入度
for (int i = 1; i <= m; i++) {
int u, v, w; scanf("%d%d%d", &u, &v, &w);
g[u].push_back({v, w});
ind[v]++;
}
// --- 第一轮：预处理入度，剪除与源点1无关的路径 ---
queue<int> q;
// 初始化距离数组，dis[1]作为全局变量默认为0，是源点
for (int i = 2; i <= n; i++) {
dis[i] = -INF;
// 将除1以外所有入度为0的点加入队列
if (ind[i] == 0) {
q.push(i);
}
}
// "空跑"一次拓扑排序，只更新入度，不计算距离
while (!q.empty()) {
int u = q.front(); q.pop();
for (pi e : g[u]) {
int v = e.first, w = e.second;
ind[v]--;
// 如果v的入度变为0，并且v不是源点1，则继续处理
if (ind[v] == 0 && v != 1) q.push(v);
}
}
// --- 第二轮：在预处理后的图上，计算从1出发的最长路 ---
// 此时的ind数组已经排除了无关路径的干扰
q.push(1); // 只将源点1作为起始点
while (!q.empty()) {
int u = q.front(); q.pop();
for (pi e : g[u]) {
int v = e.first, w = e.second;
// 状态转移：用u的最长路更新v的最长路
dis[v] = max(dis[v], dis[u] + w);
ind[v]--;
// 如果v的入度变为0，说明其所有来自1号点的前驱都已处理完毕
if (ind[v] == 0) q.push(v);
}
}
// 输出结果，如果dis[n]未被更新，则说明不可达
printf("%d\n", dis[n] == -INF ? -1 : dis[n]);
return 0;
}
习题：P7113 [NOIP2020] 排水系统
解题思路
按拓扑序计算，\(ans_i\) 的初始值为 \(1\)，对于拓扑排序过程中连向 \(v\) 的边，有 \(ans_v = \sum \dfrac{ans_u}{outdeg_u}\)。
最后输出出度为 \(0\) 的点的答案。
注意结果用分数形式保存，即分子、分母分别存储。
本题的坑点：分母最大可达 \(60^{11}\)，如果只用 long long 得分为 \(60 \sim 90\) 分。现在可以使用 __int128。
参考代码
#include <cstdio>
#include <vector>
#include <queue>
#include <utility>
using std::vector;
using std::queue;
using std::pair;
using frac = pair<__int128, __int128>; // 分子，分母
const int N = 100005;
vector<int> graph[N];
int ind[N];
frac ans[N];
__int128 gcd(__int128 x, __int128 y) {
return y == 0 ? x : gcd(y, x % y);
}
frac add(frac f1, frac f2) {
frac res;
__int128 lcm = f1.second / gcd(f1.second, f2.second) * f2.second;
res.first = lcm / f1.second * f1.first + lcm / f2.second * f2.first;
res.second = lcm;
__int128 g = gcd(res.first, res.second);
res.first /= g; res.second /= g;
return res;
}
void output(__int128 n) {
if (n > 9) output(n / 10);
putchar(n % 10 + '0');
}
int main()
{
int n, m; scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) {
ans[i] = {0, 1};
int d; scanf("%d", &d);
for (int j = 1; j <= d; j++) {
int a; scanf("%d", &a);
graph[i].push_back(a);
ind[a]++;
}
}
queue<int> q;
for (int i = 1; i <= n; i++)
if (ind[i] == 0) {
q.push(i); ans[i] = {1, 1};
}
while (!q.empty()) {
int u = q.front(); q.pop();
for (int v : graph[u]) {
frac f = {ans[u].first, ans[u].second * (__int128)graph[u].size()};
ans[v] = add(ans[v], f);
ind[v]--;
if (ind[v] == 0) q.push(v);
}
}
for (int i = 1; i <= n; i++)
if (graph[i].size() == 0) {
output(ans[i].first); printf(" "); output(ans[i].second); printf("\n");
}
return 0;
}
习题：P10530 [XJTUPC 2024] 生命游戏
解题思路
直接一轮一轮地模拟（扫描所有点 -> 找度数为 \(k\) 的点 -> 删除 -> 更新度数 -> 进入下一轮）是可行的，但效率不高。一个更高效的方法是借鉴拓扑排序的思想，拓扑排序处理的是入度为 \(0\) 的节点，而这里处理的是度数为 \(k\) 的节点，它们的核心思想是类似的：处理一批符合条件的节点，然后更新它们的邻居，将新符合条件的邻居加入待处理队列，如此往复，直到队列为空。
参考代码
#include <cstdio>
#include <vector>
using std::vector;
const int N = 1000005;
int d[N]; // d[i]: 存储节点i的当前度数
vector<int> tr[N]; // 邻接表存储树的结构
bool del[N]; // del[i]: 标记节点i是否已被删除或待删除
bool vis[N]; // vis[i]: 在主循环中，用于防止邻居被重复加入下一轮的队列
/**
* @brief DFS用于在最终的剩余图中计算连通块数量
* @param u 当前节点
*/
void dfs(int u) {
// 将u标记为已删除/已访问，防止重复计数同一个连通块
del[u] = true;
// 遍历u的邻居
for (int v : tr[u]) {
// 如果邻居v也未被删除，则递归访问它
if (del[v]) continue;
dfs(v);
}
}
int main()
{
int n, k; scanf("%d%d", &n, &k);
// --- 步骤1: 初始化 ---
// 读取树的边，建立邻接表，并计算初始度数
for (int i = 1; i < n; i++) {
int u, v; scanf("%d%d", &u, &v);
d[u]++; d[v]++;
tr[u].push_back(v); tr[v].push_back(u);
}
// vec 模拟一个队列，存放当前回合要删除的节点
vector<int> vec;
// 找到所有初始度数就为k的节点，作为第一批删除对象
for (int i = 1; i <= n; i++) {
if (d[i] == k) {
vec.push_back(i); del[i] = true;
}
}
// --- 步骤2: 迭代删除过程 ---
// 只要队列不为空，就说明还有节点要被删除
while (vec.size() > 0) {
vector<int> tmp; // tmp 模拟下一回合的队列
// 遍历当前回合要删除的所有节点 u
for (int u : vec) {
// 遍历 u 的所有邻居 v
for (int v : tr[u]) {
// 如果邻居v已经被标记为删除了，则跳过
if (del[v]) continue;
// u被删除，v的度数减一
d[v]--;
// vis数组确保一个节点在一轮中只被考虑一次
if (!vis[v]) {
tmp.push_back(v); // 将v作为下一轮的候选节点
vis[v] = true;
}
}
}
vec.clear(); // 清空当前回合的队列
// 检查所有候选节点，看它们是否满足下一轮的删除条件
for (int u : tmp)
if (d[u] == k) {
// 如果度数恰好为k，加入下一轮的删除队列
vec.push_back(u); del[u] = true;
} else {
// 如果不满足，则它不是下一轮要删除的节点
// 清除它的vis标记，以便在更后面的轮次中可以再次被考虑
vis[u] = false;
}
}
// --- 步骤3: 计算剩余图的连通块数量 ---
int ans = 0;
// 遍历所有节点
for (int i = 1; i <= n; i++) {
// 如果节点i最终没有被删除
if (!del[i]) {
// 说明找到了一个新的连通块
ans++;
// 从i开始DFS，将这个连通块的所有节点都标记掉，防止重复计数
dfs(i);
}
}
printf("%d\n", ans);
return 0;
}
例题：P1038 [NOIP2003 提高组] 神经网络
解题思路
按拓扑序计算，在向后传递的过程中注意，只有当前的 \(C\) 大于 \(0\) 才会对之后的点有贡献。
最后要统计有多少没有出度且 \(C\) 大于 \(0\) 的点，并依次输出。
参考代码
#include <cstdio>
#include <vector>
#include <queue>
#include <utility>
using std::pair;
using std::vector;
using std::queue;
using edge = pair<int, int>;
const int N = 105;
int u[N], c[N], ind[N];
vector<edge> graph[N];
int main()
{
int n, p; scanf("%d%d", &n, &p);
for (int i = 1; i <= n; i++) {
scanf("%d%d", &c[i], &u[i]);
if (c[i] == 0) c[i] -= u[i];
}
for (int i = 1; i <= p; i++) {
int u, v, w; scanf("%d%d%d", &u, &v, &w);
graph[u].push_back({v, w}); ind[v]++;
}
queue<int> q;
for (int i = 1; i <= n; i++) if (ind[i] == 0) q.push(i);
while (!q.empty()) {
int cur = q.front(); q.pop();
for (edge p : graph[cur]) {
int nxt = p.first, w = p.second;
ind[nxt]--;
if (c[cur] > 0) c[nxt] += w * c[cur];
if (ind[nxt] == 0) q.push(nxt);
}
}
bool null = true;
for (int i = 1; i <= n; i++)
if (graph[i].size() == 0 && c[i] > 0) {
null = false;
printf("%d %d\n", i, c[i]);
}
if (null) printf("NULL\n");
return 0;
}
例题：P1983 [NOIP2013 普及组] 车站分级
解题思路
希望分的级别尽量少，也就是最高级别尽量低，如果可以让每个车站取到它的最低等级，那最终的结果就是这些等级的最大值。
这就可以建图了，点显然就是每个车站，边要根据车次来定，没停的站的等级一定低于停的站，所以可以由没停的站向停的站连边，注意不要添加重边，否则边数太多。
设 \(level_i\) 表示车站 \(i\) 的最低等级，拓扑排序过程中对于边 \((u,v)\)，取 \(level_v = \max (level_v, level_u + 1)\)。
最后结果为 \(level\) 数组的最大值，极限时间复杂度 \(O(mn^2)\)，但在这题的数据上可过。
参考代码
#include <cstdio>
#include <vector>
#include <queue>
#include <algorithm>
using std::queue;
using std::vector;
using std::max;
const int N = 1005;
vector<int> graph[N];
int ind[N], level[N];
bool vis[N][N];
int main()
{
int n, m; scanf("%d%d", &n, &m);
for (int i = 1; i <= m; i++) {
int s; scanf("%d", &s);
vector<int> stop(s);
for (int j = 0; j < s; j++) scanf("%d", &stop[j]);
for (int j = 1; j < s; j++) {
for (int k1 = stop[j - 1] + 1; k1 < stop[j]; k1++) {
for (int k2 : stop) {
if (vis[k1][k2]) continue;
graph[k1].push_back(k2);
ind[k2]++;
vis[k1][k2] = true;
}
}
}
}
queue<int> q;
int ans = 0;
for (int i = 1; i <= n; i++)
if (ind[i] == 0) {
q.push(i); level[i] = 1;
}
while (!q.empty()) {
int u = q.front(); q.pop();
for (int v : graph[u]) {
level[v] = max(level[v], level[u] + 1);
ans = max(ans, level[v]);
ind[v]--;
if (ind[v] == 0) q.push(v);
}
}
printf("%d\n", ans);
return 0;
}
瓶颈在于连边的次数过多，需要减少边数。
这里的建图还可以进一步优化，对于每一趟车次可以增加一个虚拟结点，所有不停靠的车站指向这个虚拟结点，而虚拟结点又指向所有停靠的车站，这样可以将建图的边数由 \(|S_1| \times |S_2|\) 降至 \(|S_1| + |S_2|\)，其中 $|S_1| $ 和 $ |S_2|$ 分别为停靠车站的数量和不停靠车站的数量。这样的话答案为最长链的边数除以 2 再加 1。这样时间复杂度为 \(O(nm)\)。
参考代码
#include <cstdio>
#include <vector>
#include <queue>
#include <algorithm>
using std::queue;
using std::vector;
using std::max;
const int N = 2005;
vector<int> graph[N];
int ind[N], level[N];
int main()
{
int n, m; scanf("%d%d", &n, &m);
for (int i = 1; i <= m; i++) {
int s; scanf("%d", &s);
// virtual node (n+i)
int pre = 0;
for (int j = 1; j <= s; j++) {
int stop; scanf("%d", &stop);
if (j == 1) pre = stop;
graph[stop].push_back(n + i); ind[n + i]++;
for (int k = pre + 1; k < stop; k++) {
graph[n + i].push_back(k);
ind[k]++;
}
pre = stop;
}
}
queue<int> q;
int ans = 1;
for (int i = 1; i <= n + m; i++)
if (ind[i] == 0) q.push(i);
while (!q.empty()) {
int u = q.front(); q.pop();
for (int v : graph[u]) {
level[v] = max(level[v], level[u] + 1);
ans = max(ans, level[v]);
ind[v]--;
if (ind[v] == 0) q.push(v);
}
}
printf("%d\n", ans / 2 + 1);
return 0;
}
例题：P1347 排序
解题思路
矛盾就是有环，也就是拓扑排序过程中取出的元素数不够 \(n\)。
唯一解就是自始至终队列里都只有不超过 \(1\) 个元素。
如果队列里有多个备选元素，就是多解。
参考代码
#include <cstdio>
#include <vector>
#include <queue>
using std::vector;
using std::queue;
int main()
{
int n, m; scanf("%d%d", &n, &m);
vector<vector<int>> g(n);
vector<int> ind(n);
for (int i = 1; i <= m; i++) {
char buf[4]; scanf("%s", buf);
int u = buf[0] - 'A', v = buf[2] - 'A';
g[u].push_back(v); ind[v]++;
queue<int> q;
vector<int> tmp = ind;
for (int j = 0; j < n; j++) if (tmp[j] == 0) q.push(j);
bool mul = false;
vector<int> order;
while (!q.empty()) {
if (q.size() > 1) mul = true;
u = q.front(); q.pop(); order.push_back(u);
for (int v : g[u]) {
tmp[v]--;
if (tmp[v] == 0) q.push(v);
}
}
if (order.size() < n) {
printf("Inconsistency found after %d relations.\n", i);
return 0;
} else if (!mul) {
printf("Sorted sequence determined after %d relations: ", i);
for (int x : order) printf("%c", x + 'A');
printf(".\n");
return 0;
}
}
printf("Sorted sequence cannot be determined.\n");
return 0;
}
习题：P3243 [HNOI2015] 菜肴制作
解题思路
注意，本题并不是求字典序最小的拓扑序。
例如，\(4\) 种菜肴，\(2\) 在 \(4\) 前，\(3\) 在 \(1\) 前。
则如果求字典序最小的拓扑序会求出 \(2, 3, 1, 4\)，而本题实际上想要求得的结果是 \(3, 1, 2, 4\)。
考虑制作的最后一道菜肴（其出度必为 \(0\)），这道菜在满足拓扑序的情况下，编号应该尽可能大。如果最后一道菜不是可以作为最后的菜肴中编号最大的，那么将另一道编号更大的菜肴与其交换之后会使得结果更优。
最后一道菜定了之后，可以将它移出考虑范畴了。此时问题演变为剩下 \(n-1\) 道菜的制作顺序，上面的策略可以复用。
因此本题等价于按反向边建图之后求字典序最大的拓扑序，这个结果倒过来输出就是本题要求的答案。
参考代码
#include <cstdio>
#include <vector>
#include <queue>
using std::vector;
using std::priority_queue;
const int N = 100005;
vector<int> graph[N];
int ind[N], ans[N];
void solve() {
int n, m; scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) {
graph[i].clear(); ind[i] = 0;
}
for (int i = 1; i <= m; i++) {
int x, y; scanf("%d%d", &x, &y);
graph[y].push_back(x); ind[x]++;
}
priority_queue<int> q;
for (int i = 1; i <= n; i++) if (ind[i] == 0) q.push(i);
int idx = 0;
while (!q.empty()) {
int u = q.top(); q.pop();
ans[++idx] = u;
for (int v : graph[u]) {
ind[v]--;
if (ind[v] == 0) q.push(v);
}
}
if (idx < n) printf("Impossible!");
else for (int i = n; i >= 1; i--) printf("%d ", ans[i]);
printf("\n");
}
int main()
{
int t; scanf("%d", &t);
for (int i = 1; i <= t; i++) {
solve();
}
return 0;
}
例题：P4376 [USACO18OPEN] Milking Order G
分析：分两步，第一步求最大的符合条件的 \(X\)，第二步求字典序最小的方案。
先看第一步，最朴素的想法是暴力枚举 \(X\)，跑拓扑排序判断是否有可行解，这一步时间复杂度为 \(O((n+m)m)\)。
想要进一步优化需要观察到 \(X\) 对结果的影响有单调性，可以二分答案求出最大的 \(X\)，这样时间复杂度降为 \(O((n+m) \log m)\)。
第二步，求字典序最小的方案。
首先需要理解拓扑排序过程中队列里的节点的含义，这些点是目前入度为 \(0\) 的点（所有前置依赖都已释放），它们之间没有必然顺序，所以实际上不一定非得用队列存储，只是通常会使用队列来实现。
现在要求字典序最小的方案，也就是每次要取出的点是可选的点中编号最小的，因此可以把队列换成优先队列，让编号小的先出队。
这一步时间复杂度为 \(O((n+m) \log m)\)，注意第一步用二分答案计算 \(X\) 时，判定是否有可行解应该使用朴素的队列，否则时间复杂度里就会有两个 \(\log\)。
参考代码
#include <cstdio>
#include <vector>
#include <queue>
using std::vector;
using std::queue;
using std::priority_queue;
using std::greater;
const int N = 200005;
vector<int> order[N], graph[N];
int ind[N], res[N];
void init(int n) {
for (int i = 1; i <= n; i++) {
graph[i].clear(); ind[i] = 0;
}
}
bool check(int n, int x) {
init(n);
for (int i = 1; i <= x; i++) {
for (int j = 1; j < order[i].size(); j++) {
int pre = order[i][j - 1], cur = order[i][j];
graph[pre].push_back(cur); ind[cur]++;
}
}
queue<int> q;
for (int i = 1; i <= n; i++) if (ind[i] == 0) q.push(i);
while (!q.empty()) {
int u = q.front(); q.pop();
for (int v : graph[u]) {
ind[v]--;
if (ind[v] == 0) q.push(v);
}
}
for (int i = 1; i <= n; i++) if (ind[i] != 0) return false;
return true;
}
int main()
{
int n, m; scanf("%d%d", &n, &m);
for (int i = 1; i <= m; i++) {
int cnt; scanf("%d", &cnt);
for (int j = 1; j <= cnt; j++) {
int x; scanf("%d", &x); order[i].push_back(x);
}
}
int ans = 0, l = 1, r = m;
while (l <= r) {
int mid = (l + r) / 2;
if (check(n, mid)) {
l = mid + 1; ans = mid;
} else {
r = mid - 1;
}
}
priority_queue<int, vector<int>, greater<int>> q;
init(n);
for (int i = 1; i <= ans; i++) {
for (int j = 1; j < order[i].size(); j++) {
int pre = order[i][j - 1], cur = order[i][j];
graph[pre].push_back(cur); ind[cur]++;
}
}
for (int i = 1; i <= n; i++) if (ind[i] == 0) q.push(i);
int cnt = 0;
while (!q.empty()) {
cnt++; res[cnt] = q.top(); q.pop();
for (int v : graph[res[cnt]]) {
ind[v]--;
if (ind[v] == 0) q.push(v);
}
}
for (int i = 1; i <= n; i++) printf("%d ", res[i]);
return 0;
}
例题：P7077 [CSP-S2020] 函数调用
分析：先从简单的操作入手。
如果只有操作 \(1\)，直接单点加即可。
如果只有操作 \(2\)，用一个变量维护全局乘的数即可。
如果只有操作 \(1,2\)，会发现当一个操作 \(1\) 后接了若干操作 \(2\) 时，该操作 \(1\) 加的数会被乘后续操作 \(2\) 的乘积，也可以看作把这次操作 \(1\) 调用后续操作 \(2\) 的乘积次。
如果只有操作 \(1,3\)，可以设 \(cnt_i\) 表示函数 \(i\) 的调用次数，对调用的关系形成的 DAG 进行拓扑排序可以求得所有的 \(cnt\) 值，若 \(u\) 调用 \(v\)，则有 \(cnt_v \leftarrow cnt_v + cnt_u\)。
如果只有操作 \(2,3\)，同样地，可以设 \(mul_i\) 表示调用函数 \(i\) 之后全局将会乘多少，按照调用关系形成的 DAG 进行记忆化搜索（或用反向边建图进行拓扑排序）计算得出所有的 \(mul\)，若 \(u\) 调用 \(v\)，则有 \(mul_u \leftarrow mul_u \times mul_v\)。
参考代码
#include <cstdio>
#include <vector>
#include <queue>
using std::vector;
using std::queue;
const int N = 100005;
const int MOD = 998244353;
int n, m, q, a[N], t[N], p[N], add[N], mul[N], f[N];
int ind[N], rev_ind[N], cnt[N];
vector<int> graph[N], rev_graph[N];
void func(int u) {
if (t[u] == 1) {
int idx = p[u];
a[idx] = (a[idx] + add[u]) % MOD;
} else if (t[u] == 2) {
for (int i = 1; i <= n; i++) {
a[i] = 1ll * a[i] * mul[u] % MOD;
}
} else {
for (int g : graph[u]) {
func(g);
}
}
}
bool check_no_3() { // 没有操作3，只有1和2
for (int i = 1; i <= m; i++) {
if (graph[i].size()) return false;
}
return true;
}
void solve_no_3() {
vector<int> add_num(n + 1);
int global_mul = 1;
for (int i = q; i >= 1; i--) {
int u = f[i];
if (t[u] == 1) {
int idx = p[u];
add_num[idx] = (add_num[idx] + 1ll * global_mul * add[u] % MOD) % MOD;
} else {
global_mul = 1ll * global_mul * mul[u] % MOD;
}
}
for (int i = 1; i <= n; i++) {
a[i] = 1ll * a[i] * global_mul % MOD;
a[i] = (a[i] + add_num[i]) % MOD;
}
}
int quickpow(int x, int y) {
int res = 1;
while (y > 0) {
if (y % 2 == 1) res = 1ll * res * x % MOD;
x = 1ll * x * x % MOD;
y /= 2;
}
return res;
}
bool check_no_2() { // 没有操作2，只有1和3
for (int i = 1; i <= m; i++)
if (t[i] == 2) return false;
return true;
}
void solve_no_2() {
for (int i = 1; i <= q; i++) cnt[f[i]]++;
queue<int> que;
for (int i = 1; i <= m; i++) if (ind[i] == 0) que.push(i);
while (!que.empty()) {
int u = que.front(); que.pop();
for (int v : graph[u]) {
cnt[v] = (cnt[v] + cnt[u]) % MOD;
ind[v]--;
if (ind[v] == 0) que.push(v);
}
}
for (int i = 1; i <= m; i++) {
if (t[i] == 1) {
a[p[i]] = (a[p[i]] + 1ll * cnt[i] * add[i] % MOD) % MOD;
}
}
}
bool check_no_1() { // 没有操作1，只有2和3
for (int i = 1; i <= m; i++)
if (t[i] == 1) return false;
return true;
}
void solve_no_1() {
queue<int> que;
for (int i = 1; i <= m; i++) if (rev_ind[i] == 0) que.push(i);
while (!que.empty()) {
int u = que.front(); que.pop();
for (int v : rev_graph[u]) {
mul[v] = 1ll * mul[u] * mul[v] % MOD;
rev_ind[v]--;
if (rev_ind[v] == 0) que.push(v);
}
}
int global_mul = 1;
for (int i = 1; i <= q; i++) global_mul = 1ll * global_mul * mul[f[i]] % MOD;
for (int i = 1; i <= n; i++) a[i] = 1ll * a[i] * global_mul % MOD;
}
int main()
{
scanf("%d", &n);
for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
scanf("%d", &m);
for (int i = 1; i <= m; i++) {
scanf("%d", &t[i]);
if (t[i] == 1) {
scanf("%d%d", &p[i], &add[i]);
mul[i] = 1;
} else if (t[i] == 2) {
scanf("%d", &mul[i]);
} else {
int c; scanf("%d", &c); mul[i] = 1;
for (int j = 1; j <= c; j++) {
int g; scanf("%d", &g);
graph[i].push_back(g); ind[g]++;
rev_graph[g].push_back(i); rev_ind[i]++;
}
}
}
scanf("%d", &q);
for (int i = 1; i <= q; i++) {
scanf("%d", &f[i]);
}
if (check_no_3()) {
solve_no_3();
} else if (check_no_2()) {
solve_no_2();
} else if (check_no_1()) {
solve_no_1();
} else {
for (int i = 1; i <= q; i++) func(f[i]);
}
for (int i = 1; i <= n; i++) printf("%d ", a[i]);
return 0;
}
为了方便，可以建立一个虚点 \(0\)，表示“主函数”，也就是由 \(0\) 依次调用那 \(Q\) 个要执行的函数。
在操作 \(1,3\) 的基础上结合 \(1,2\) 混合的处理方式。
对于拓扑排序过程中遇到的每个节点 \(u\)，维护一个变量 \(nowmul\) 表示 \(u\) 调用 \(v\) 以后在 \(u\) 的调用过程中后续还要乘多少，也就等价于在一次 \(u\) 的执行过程中 \(v\) 要执行 \(nowmul\) 次，所以执行次数 \(cnt_v \leftarrow cnt_v + cnt_u \times nowmul\)，并且将 \(nowmul \leftarrow nowmul \times mul_v\)，因为 \(u\) 要调用 \(v\) 之前的函数时，\(v\) 带来的乘法效果就需要考虑了。
对于初始化，只需要将 \(cnt_0\) 设为 \(1\) 即可，最后答案是先把每个数乘 \(mul_0\)，再遍历每个函数，如果是操作 \(1\)，则将该单点加执行 \(cnt_i\) 次，即 \(a_{p_i} \leftarrow a_{p_i} + v_i \times cnt_i\)。
注意遍历 \(u\) 指出的边时需要按输入的倒序。
参考代码
#include <cstdio>
#include <vector>
#include <queue>
using std::vector;
using std::queue;
const int N = 100005;
const int MOD = 998244353;
vector<int> g[N], rev_g[N];
int ind[N], rev_ind[N], a[N], t[N], p[N], add[N], mul[N], cnt[N];
int main()
{
int n; scanf("%d", &n);
for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
int m; scanf("%d", &m);
for (int i = 1; i <= m; i++) {
scanf("%d", &t[i]);
if (t[i] == 1) {
scanf("%d%d", &p[i], &add[i]);
mul[i] = 1;
} else if (t[i] == 2) {
scanf("%d", &mul[i]);
} else {
mul[i] = 1;
int c; scanf("%d", &c);
for (int j = 1; j <= c; j++) {
int gid; scanf("%d", &gid);
g[i].push_back(gid); ind[gid]++;
rev_g[gid].push_back(i); rev_ind[i]++;
}
}
}
int q; scanf("%d", &q);
for (int i = 1; i <= q; i++) {
int f; scanf("%d", &f);
g[0].push_back(f); ind[f]++;
rev_g[f].push_back(0); rev_ind[0]++;
}
mul[0] = 1; cnt[0] = 1;
queue<int> que;
for (int i = 0; i <= m; i++) {
if (rev_ind[i] == 0) que.push(i);
}
while (!que.empty()) {
int u = que.front(); que.pop();
for (int v : rev_g[u]) {
mul[v] = 1ll * mul[v] * mul[u] % MOD;
if (--rev_ind[v] == 0) que.push(v);
}
}
for (int i = 1; i <= n; i++) a[i] = 1ll * a[i] * mul[0] % MOD;
for (int i = 0; i <= m; i++) if (ind[i] == 0) que.push(i);
while (!que.empty()) {
int u = que.front(); que.pop();
int nowmul = 1;
if (g[u].size() > 0) {
for (int i = (int)g[u].size() - 1; i >= 0; i--) {
int v = g[u][i];
cnt[v] = (cnt[v] + 1ll * cnt[u] * nowmul % MOD) % MOD;
if (--ind[v] == 0) que.push(v);
nowmul = 1ll * nowmul * mul[v] % MOD;
}
}
}
for (int i = 1; i <= m; i++) {
if (t[i] == 1) {
a[p[i]] = (a[p[i]] + 1ll * add[i] * cnt[i] % MOD) % MOD;
}
}
for (int i = 1; i <= n; i++) printf("%d ", a[i]);
return 0;
}
浙公网安备 33010602011771号