树上前缀和与差分

树上前缀和

设 \(sum_i\) 表示根节点到节点 \(i\) 的权值总和。
则有：

对于点权，\(x,y\) 路径上的和为 \(sum_x + sum_y - sum_{lca} - sum_{fa_{lca}}\)。
对于边权，\(x,y\) 路径上的和为 \(sum_x + sum_y - 2 \times sum_{lca}\)。

例题：P4427 [BJOI2018] 求和

分析：因为 \(k\) 不大，可以把 \(k\) 作为一维信息。预处理出 \(sum_{i,k}\) 表示根节点到节点 \(i\) 的深度的 \(k\) 次方和，这个过程的时间复杂度为 \(O(nk)\)。

要维护的是求和，其具备逆运算，也就是减法，可以把 \((u,v)\) 拆成 \((root, u)\) 和 \((root, v)\) 去掉 \((root, lca)\)。这里因为是对点的计算而不是对边的，因此答案的计算方法是 \(sum_{u,k} + sum_{v, k} - sum_{lca, k} - sum_{fa_{lca},k}\)。

参考代码

#include <cstdio>
#include <vector>
#include <algorithm>
using std::swap;
using std::vector;
const int N = 3e5 + 5;
const int K = 55;
const int LOG = 19;
const int MOD = 998244353;
vector<int> tree[N];
int fa[N][LOG], depth[N], sum[N][K];
void dfs(int u, int pre) {
    depth[u] = depth[pre] + 1;
    int d = 1;
    for (int i = 0; i < K; i++) {
        sum[u][i] = (sum[pre][i] + d) % MOD;
        d = 1ll * d * depth[u] % MOD;
    } 
    fa[u][0] = pre;
    for (int v : tree[u]) {
        if (v == pre) continue;
        dfs(v, u);
    }
}
int lca(int x, int y) {
    if (depth[x] < depth[y]) swap(x, y);
    int delta = depth[x] - depth[y];
    for (int i = LOG - 1; i >= 0; i--)
        if (delta & (1 << i)) x = fa[x][i];
    if (x == y) return x;
    for (int i = LOG - 1; i >= 0; i--) {
        if (fa[x][i] != fa[y][i]) {
            x = fa[x][i]; y = fa[y][i];
        }
    }
    return fa[x][0];
}
int main()
{
    int n; scanf("%d", &n);
    for (int i = 1; i < n; i++) {
        int x, y; scanf("%d%d", &x, &y);
        tree[x].push_back(y);
        tree[y].push_back(x);
    }
    depth[0] = -1;
    dfs(1, 0);
    for (int i = 1; i < LOG; i++) {
        for (int j = 1; j <= n; j++) fa[j][i] = fa[fa[j][i - 1]][i - 1];
    }
    int m; scanf("%d", &m);
    while (m--) {
        int i, j, k; scanf("%d%d%d", &i, &j, &k);
        int lca_ij = lca(i, j), f = fa[lca_ij][0];
        int ans1 = (sum[i][k] + MOD - sum[f][k]) % MOD;
        int ans2 = (sum[j][k] + MOD - sum[lca_ij][k]) % MOD;
        printf("%d\n", (ans1 + ans2) % MOD);
    }
    return 0;
}

例题：P1084 [NOIP2012 提高组] 疫情控制

分析：二分答案 \(x\)。

在 check 时，最直接的想法是让每支军队都往根方向走尽量走，可以用前缀和预处理每个节点到根节点的距离，利用倍增法求出在 \(x\) 以内往上最多能走到哪里，如果走不到根就直接停在尽可能高的地方。

如果能走到根，要暂时把这支军队存起来，因为有可能需要跨过根去根的其他子树。把这些能到根的军队是哪棵子树的以及它如果到根之后还剩多少时间。

接着看凭借走不到根的那些军队已经覆盖了根的哪些子树，对于还没覆盖好的子树，就要靠那些存下来的军队。

首先考虑一种特殊情况，如果存下来的军队里某个军队走到根后不够时间返回自己的子树，那么就直接让它守自己这棵子树，因为与其让它去个离根更近的别的子树，然后让别的军队守它的子树，还不如直接调别的军队守别的子树情况更好，因为能守它子树的军队一定比它的剩余时间长。

对于剩下的军队和剩下的需要守的子树，考虑如何匹配。

对需要守的子树按根到子树的距离从小到大排序，逐一找到能守它的剩余时间最短的军队，如果每棵子树都能被守，\(x\) 就可行，否则 \(x\) 就不可行，整体时间复杂度为 \(O(n \log n \log \sum w)\)。

参考代码

#include <cstdio>
#include <vector>
#include <utility>
#include <algorithm>
using std::vector;
using std::pair;
using std::sort;
using ll = long long;
using edge = pair<int, int>;
const int N = 50005;
const int LOG = 16;
int n, m, f[N][LOG], city[N], weight[N];
ll sum[N];
bool cover[N];
vector<pair<int, int>> tree[N];
void dfs1(int u, int fa) {
    for (edge e : tree[u]) {
        int v = e.first, w = e.second;
        if (v == fa) continue;
        f[v][0] = u; sum[v] = sum[u] + w;
        dfs1(v, u);
    }
}
void dfs2(int u, int fa) {
    int child = 0;
    bool flag = true;
    for (edge e : tree[u]) {
        int v = e.first;
        if (v == fa) continue;
        dfs2(v, u);
        if (!cover[v]) {
            flag = false;
        }
        child++;
    }
    if (!cover[u] && child > 0 && flag) cover[u] = true;
}
bool check(ll x) {
    for (int i = 1; i <= n; i++) cover[i] = false;
    vector<pair<int, ll>> vec;
    for (int i = 1; i <= m; i++) {
        int u = city[i];
        for (int j = LOG - 1; j >= 0; j--) {
            int ancestor = f[u][j];
            if (ancestor == 0 || ancestor == 1) continue;
            if (sum[city[i]] - sum[ancestor] <= x) u = ancestor;
        }
        if (f[u][0] == 1 && sum[city[i]] < x) {
            vec.push_back({u, x - sum[city[i]]});
        } else {
            cover[u] = true; 
        }
    }
    dfs2(1, 0);
    vector<ll> rest;
    for (auto p : vec) {
        if (!cover[p.first] && p.second < weight[p.first]) {
            cover[p.first] = true;
        } else {
            rest.push_back(p.second);
        }
    }
    sort(rest.begin(), rest.end(), [](ll lhs, ll rhs) {
        return lhs < rhs;
    });
    int idx = 0;
    for (edge e : tree[1]) {
        if (!cover[e.first]) {
            bool ok = false;
            while (idx < rest.size()) {
                if (rest[idx] >= e.second) {
                    idx++; ok = true; break;
                } else idx++;
            }
            if (!ok) return false; 
        }
    }
    return true;
}
int main()
{
    scanf("%d", &n);
    ll tot = 0;
    for (int i = 1; i < n; i++) {
        int u, v, w; scanf("%d%d%d", &u, &v, &w);
        tree[u].push_back({v, w});
        tree[v].push_back({u, w});
        tot += w;
    }
    scanf("%d", &m);
    if (m < tree[1].size()) {
        printf("-1\n");
    } else {
        dfs1(1, 0);
        for (int j = 1; j < LOG; j++)
            for (int i = 1; i <= n; i++)
                f[i][j] = f[f[i][j - 1]][j - 1];
        for (edge e : tree[1]) weight[e.first] = e.second;
        sort(tree[1].begin(), tree[1].end(), [](edge lhs, edge rhs) {
            return lhs.second < rhs.second;
        });
        for (int i = 1; i <= m; i++) scanf("%d", &city[i]);
        ll l = 0, r = tot, ans = tot;
        while (l <= r) {
            ll mid = (l + r) / 2;
            if (check(mid)) {
                r = mid - 1; ans = mid;
            } else {
                l = mid + 1;
            }
        }
        printf("%lld\n", ans);
    }
    return 0;
}

树上差分

树上差分可以理解为对树上的某一段路径进行差分操作，这里的路径可以类比一维数组的区间进行理解。例如在对树上的一些路径进行频繁操作，并且询问某条边或者某个点在经过操作后的值的时候，就可以运用树上差分思想。

树上差分可以用于快速统计有多少条路径经过每个点或每条边。

点差分

例题：P3128 [USACO15DEC] Max Flow P

问题描述：有 \(n\) 个节点，用 \(n-1\) 条边连接，所有节点都连通。给出 \(k\) 条路径，第 \(i\) 条路径为节点 \(s_i\) 到 \(t_i\)。每给出一条路径，路径上所有节点的权值加 \(1\)。输出最大权值点的权值。
数据范围：\(2 \le n \le 50000, 1 \le k \le 100000\)

分析：树上两点 \(u,v\) 的路径指的是最短路径。可以把 \(u \rightarrow v\) 的路径分为两个部分：\(u \rightarrow LCA(u,v)\) 和 \(LCA(u,v) \rightarrow v\)。

先考虑简单的思路。首先对每条路径求 LCA，分别以 \(u\) 和 \(v\) 为起点到 LCA，把路径上每个节点的权值加 \(1\)；然后对所有路径进行类似操作。把路径上每个节点加 \(1\) 的操作的复杂度为 \(O(n)\)，共 \(k\) 次操作，会超时。

本题的关键是如何记录路径上每个节点的修改。显然，如果真的对每个节点都记录修改，肯定会超时。我们可以利用差分，因为差分的用途是“把区间问题转换为端点问题”，适用这种情况。

给定数组 \(a\)，定义差分数组 \(D[k]=a[k]-a[k-1]\)，即数组相邻元素的差。

从差分数组的定义可以推出：\(a[k]=D[1]+D[2]+ \cdots + D[k] = \sum\limits_{i=1}^{k} D[i]\)

这个式子描述了 \(a\) 和 \(D\) 的关系，即“差分是前缀和的逆运算” ，它把求 \(a[k]\) 转换为求 \(D\) 的前缀和。

对于区间 \([L,R]\) 的修改问题，比如把区间内每个元素都加上 \(d\)，则可以对区间的两个端点 \(L\) 和 \(R+1\) 做以下操作：

把 \(D[L]\) 加上 \(d\)；
把 \(D[R+1]\) 减去 \(d\)。

对 \(D\) 求前缀和，则可得到 \(a\) 数组，以上的更新相当于：

\(1 \le x < L\)，\(a[x]\) 不变；
\(L \le x \le R\)，\(a[x]\) 增加了 \(d\)；
\(R < x \le N\)，\(a[x]\) 不变，因为被 \(D[R+1]\) 中减去的 \(d\) 抵消了。

利用差分能够把区间修改问题转换为只用端点做记录。如果不用差分数组，区间内每个元素都需要修改，时间复杂度为 \(O(n)\)；转换为只修改两个端点后，时间复杂度降到 \(O(1)\)，这就是差分的重要作用。

把差分思想用到树上，只需要把树上路径转换为区间即可。把一条路径 \(u \rightarrow v\) 分为两部分：\(u \rightarrow LCA(u,v)\) 和 \(LCA(u,v) \rightarrow v\)，这样每条路径都可以当成一个区间处理。

记 \(LCA(u,v)=R\)，并记 \(R\) 的父节点为 \(F=fa[R]\)，要把路径上每个节点权值加 \(1\)，有：

路径 \(u \rightarrow R\) 这个区间上，\(D[u]++\)，\(D[F]--\)；
路径 \(v \rightarrow R\) 这个区间上，\(D[v]++\)，\(D[F]--\)。

经过以上操作，能通过 \(D\) 计算出 \(u \rightarrow v\) 上每个节点的权值。不过，由于两条路径在 \(R\) 和 \(F\) 这里重合了，这两个步骤把 \(D[R]\) 加了两次，把 \(D[F]\) 减了两次，需要调整为 \(D[R]--\) 和 \(D[F]--\)。

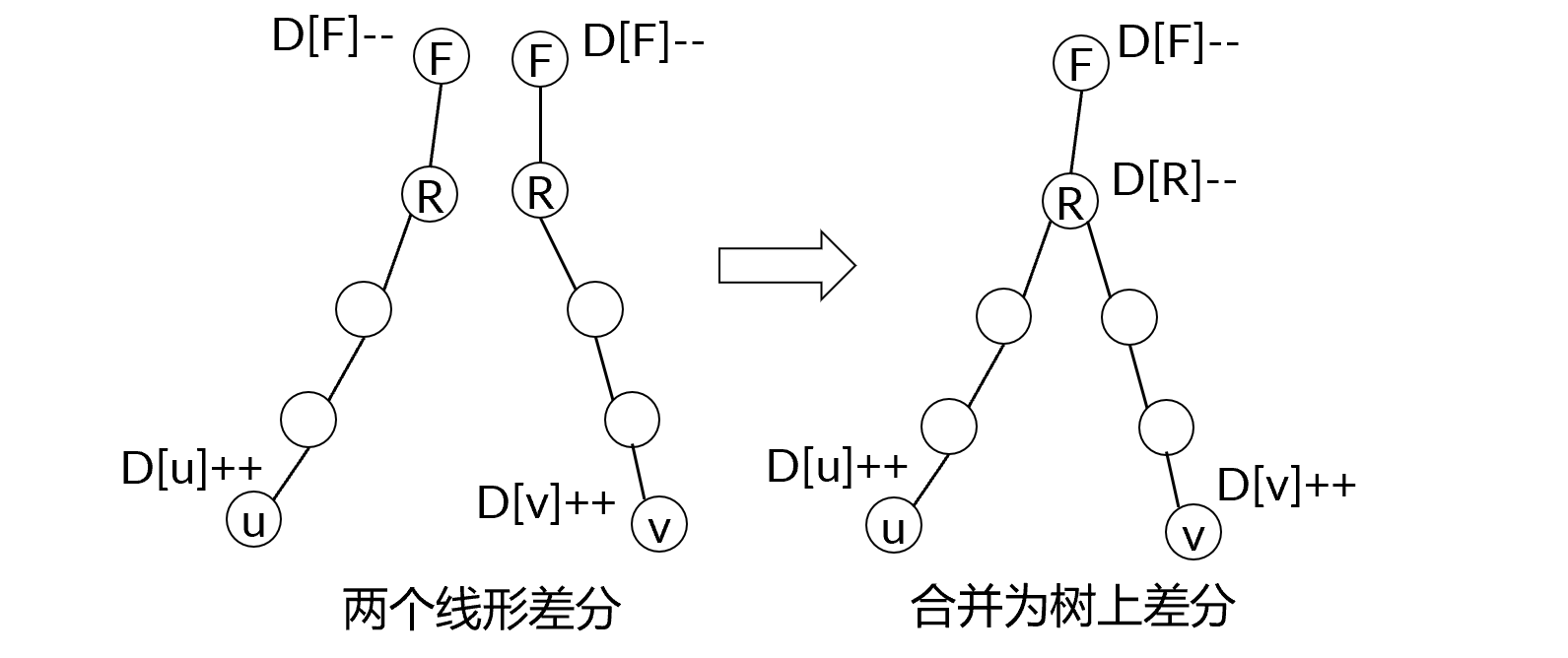
在本题中，对每条路径都用倍增法求一次 LCA，并做一次差分操作。当对于所有路径都操作完成后，再做一次 DFS，求出每个节点的权值，所有权值中的最大值即为答案。

\(k\) 次 LCA 的时间复杂度为 \(O(n \log n + k \log n)\)；最后做一次 DFS，时间复杂度为 \(O(n)\)；总的时间复杂度为 \(O((n+k) \log n)\)。

参考代码

#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
const int N = 50005;
const int LOG = 16;
vector<int> tree[N];
int d[N], fa[N][LOG], a[N], ans;
void dfs(int cur, int pre) {
    d[cur] = d[pre] + 1;
    fa[cur][0] = pre;
    for (int i = 1; i < LOG; i++) fa[cur][i] = fa[fa[cur][i - 1]][i - 1];
    for (int nxt : tree[cur])
        if (nxt != pre) dfs(nxt, cur);
}
int lca(int x, int y) {
    if (d[x] < d[y]) swap(x, y);
    int len = d[x] - d[y];
    for (int i = LOG - 1; i >= 0; i--) 
        if (1 << i <= len) {
            x = fa[x][i]; len -= 1 << i;
        }
    if (x == y) return x;
    for (int i = LOG - 1; i >= 0; i--) 
        if (fa[x][i] != fa[y][i]) {
            x = fa[x][i]; y = fa[y][i];
        }
    return fa[x][0];
}
void calc(int cur, int pre) {
    for (int nxt : tree[cur])
        if (nxt != pre) {
            calc(nxt, cur); 
            a[cur] += a[nxt];
        } 
    ans = max(ans, a[cur]);
}
int main()
{
    int n, k;
    scanf("%d%d", &n, &k);
    for (int i = 1; i < n; i++) {
        int x, y;
        scanf("%d%d", &x, &y);
        tree[x].push_back(y); tree[y].push_back(x);
    }
    dfs(1, 0); // 计算每个节点的深度并预处理fa数组
    while (k--) {
        int s, t;
        scanf("%d%d", &s, &t);
        int r = lca(s, t);
        a[s]++; a[t]++; a[r]--; a[fa[r][0]]--; // 树上差分
    }  
    calc(1, 0); // 用差分数组求每个节点的权值
    printf("%d\n", ans);
    return 0;
}

边差分

例题：P6869 [COCI2019-2020#5] Putovanje

显然针对每一条边只会考虑购买单程票和多程票的一种，这取决于该条边被经过的次数 \(k\)，这样一来这条边上的最少花费是 \(\min (k c_1, c_2)\)。

这里需要根据若干条路径计算出每条边经过的次数，可以借助差分思想，注意它和点差分不同。对于边相关的问题，一般我们会将每个点与它父亲节点相连的边与该点绑定，从而将边上信息的维护转化为对点的信息的维护。

参考代码

#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 200005;
const int LOG = 19;
vector<int> tree[N];
int d[N], fa[N][LOG], cnt[N], a[N], b[N], c1[N], c2[N];
void dfs(int cur, int pre) {
    d[cur] = d[pre] + 1;
    fa[cur][0] = pre;
    for (int i = 1; i < LOG; i++) fa[cur][i] = fa[fa[cur][i - 1]][i - 1];
    for (int nxt : tree[cur]) 
        if (nxt != pre) dfs(nxt, cur);
}
int lca(int x, int y) {
    if (d[x] < d[y]) swap(x, y);
    int len = d[x] - d[y];
    for (int i = LOG - 1; i >= 0; i--) 
        if ((1 << i) <= len) {
            x = fa[x][i]; len -= 1 << i;
        }
    if (x == y) return x;
    for (int i = LOG - 1; i >= 0; i--)
        if (fa[x][i] != fa[y][i]) {
            x = fa[x][i]; y = fa[y][i];
        }
    return fa[x][0];
}
void calc(int cur, int pre) {
    for (int nxt : tree[cur]) 
        if (nxt != pre) {
            calc(nxt, cur);
            cnt[cur] += cnt[nxt];
        }
}
int main()
{
    int n;
    scanf("%d", &n);
    for (int i = 1; i < n; i++) {
        scanf("%d%d%d%d", &a[i], &b[i], &c1[i], &c2[i]);
        tree[a[i]].push_back(b[i]);
        tree[b[i]].push_back(a[i]);
    }
    dfs(1, 0);
    for (int i = 1; i < n; i++) {
        int r = lca(i, i + 1);
        cnt[i]++; cnt[i + 1]++; cnt[r] -= 2;
    }
    calc(1, 0);
    LL ans = 0;
    for (int i = 1; i < n; i++) {
        if (d[a[i]] > d[b[i]]) ans += min(1ll * c1[i] * cnt[a[i]], 1ll * c2[i]);
        else ans += min(1ll * c1[i] * cnt[b[i]], 1ll * c2[i]);
    }
    printf("%lld\n", ans);
    return 0;
}

例题：P2680 [NOIP2015 提高组] 运输计划

分析：题目的意思是求将一条边边权修改为 \(0\) 后，\(m\) 条路径的最大边权和最小是多少。

最大值最小、最小值最大这类问题往往和二分答案有关。

设当前判断的答案是 \(x\)，则路径长度大于 \(x\) 的需要有一条边被改造，但是全局上只能改一条边，所以必须改这些路径的公共边。

可以用树上边差分统计每条边的经过次数，只有经过次数等于要改的路径条数的边是有效的，显然应该改这样的边中边权最大的，求出这个值。

最后检查所有要改的路径，看减去这个值能否使边权和小于等于 \(x\)，如果都能做到那么这个答案就可行。

参考代码

#include <cstdio>
#include <utility>
#include <vector>
#include <algorithm>
using std::swap;
using std::max;
using std::vector;
using std::pair;
using edge = pair<int, int>; // (点,边权)
const int N = 300005;
const int LOG = 19;
int n, m, d[N], f[N][LOG], sum[N], cnt[N], a[N], b[N], dis[N], lca[N];
vector<edge> tree[N];
void dfs(int u, int fa) {
    for (edge e : tree[u]) {
        int v = e.first, w = e.second;
        if (v == fa) continue;
        d[v] = d[u] + 1; f[v][0] = u;
        sum[v] = sum[u] + w;
        dfs(v, u);
    }
}
int query(int x, int y) {
    if (d[x] < d[y]) swap(x, y);
    int delta = d[x] - d[y];
    for (int i = LOG - 1; i >= 0; i--)
        if (delta & (1 << i)) x = f[x][i];
    if (x == y) return x;
    for (int i = LOG - 1; i >= 0; i--)
        if (f[x][i] != f[y][i]) {
            x = f[x][i]; y = f[y][i];
        }
    return f[x][0];
}
void calc(int u, int fa) { // 差分之后计算每条边经过次数
    for (edge e : tree[u]) {
        int v = e.first;
        if (v == fa) continue;
        calc(v, u);
        cnt[u] += cnt[v];
    }
}
bool check(int x) {
    for (int i = 1; i <= n; i++) cnt[i] = 0;
    int c = 0; // 需要改变多少个运输计划
    for (int i = 1; i <= m; i++) {
        if (dis[i] > x) {
            c++; cnt[a[i]]++; cnt[b[i]]++; cnt[lca[i]] -= 2;
        }
    }
    calc(1, 0);
    int maxw = 0;
    for (int i = 1; i <= n; i++) {
        // f[i][0]->i
        int fa = f[i][0], w = sum[i] - sum[fa];
        if (cnt[i] == c && w > maxw) maxw = w;
    }
    for (int i = 1; i <= m; i++)
        if (dis[i] - maxw > x) return false;
    return true;
}
int main()
{
    scanf("%d%d", &n, &m);
    int maxw = 0;
    for (int i = 1; i < n; i++) {
        int u, v, w; scanf("%d%d%d", &u, &v, &w);
        if (w > maxw) maxw = w;
        tree[u].push_back({v, w});
        tree[v].push_back({u, w});
    }
    dfs(1, 0);
    for (int j = 1; j < LOG; j++)
        for (int i = 1; i <= n; i++)
            f[i][j] = f[f[i][j - 1]][j - 1];
    int r = 0;
    for (int i = 1; i <= m; i++) {
        scanf("%d%d", &a[i], &b[i]);
        // 预处理每个运输计划的lca和完成时长
        lca[i] = query(a[i], b[i]);
        dis[i] = sum[a[i]] + sum[b[i]] - 2 * sum[lca[i]];
        if (dis[i] > r) r = dis[i];
    }
    // 控制二分上下界可提高效率
    int ans = r, l = max(r - maxw, 0);
    while (l <= r) {
        int mid = (l + r) / 2;
        if (check(mid)) {
            r = mid - 1; ans = mid;
        } else {
            l = mid + 1;
        }
    }
    printf("%d\n", ans);
    return 0;
}

子树差分

例题：P3605 [USACO17JAN] Promotion Counting P

给定一棵 \(n\) 个点的树，每个点有点权，求每个点子树内点权大于自身的点的数量，\(n \le 10^5\)。

解题思路

大于某个数值的点的数量显然可以通过树状数组维护，关键是怎么精准地计算到单棵子树内。

如果在 DFS 过程中更新树状数组，这样维护的是 DFS 过程中到目前这个点为止各个数值出现的次数，不一定是单棵子树。

考虑 DFS 的过程中一个点会进出（递归与回溯）各一次，实际上进入这个点时，该点的子树信息还没更新到树状数组中，而出这个点时，该点的子树信息已经都加入到树状数组中，因此这两个时间点查询的差值就是该子树的贡献。这种思想被称为子树差分。

参考代码

#include <cstdio>
#include <vector>
#include <algorithm>
const int N = 100005;
int n, p[N], ans[N], c[N];
std::vector<int> tr[N], num;
int lowbit(int x) {
    return x & -x;
}
void add(int x) {
    while (x <= n) {
        c[x]++; x += lowbit(x);
    }
}
int query(int x) {
    int res = 0;
    while (x > 0) {
        res += c[x]; x -= lowbit(x);
    }
    return res;
}
int discretize(int x) {
    return std::lower_bound(num.begin(), num.end(), x) - num.begin() + 1;
}
void dfs(int u) {
    int tmp = query(n) - query(p[u]);
    add(p[u]);
    for (int v : tr[u]) {
        dfs(v);
    }
    ans[u] = query(n) - query(p[u]) - tmp;
}
int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) {
        scanf("%d", &p[i]);
        num.push_back(p[i]);
    }
    std::sort(num.begin(), num.end());
    num.erase(std::unique(num.begin(), num.end()), num.end());
    for (int i = 1; i <= n; i++) p[i] = discretize(p[i]);
    for (int i = 2; i <= n; i++) {
        int boss; scanf("%d", &boss);
        tr[boss].push_back(i);
    }
    dfs(1);
    for (int i = 1; i <= n; i++) printf("%d\n", ans[i]);
    return 0;
}

例题：P1600 [NOIP2016 提高组] 天天爱跑步

解题思路

测试点 \(1 \sim 5\)

暴力做法是对于每条路径，模拟 \(s \rightarrow lca\) 和 \(t \rightarrow lca\) 的爬升过程，看到达时间是否正好是 \(w_x\)，统计结果。时间复杂度为 \(O(nm)\)。

测试点 \(6 \sim 8\)

当树退化成一条链时，对于每个观察员 \(x\) 而言，相当于询问有多少条 \(s = x - w_x\) 并且 \(t \ge x\) 的路径，以及有多少条 \(s = x + w_x\) 并且 \(t \le x\) 的路径。因此可以记录每个起点对应哪些终点，排序后二分即可计算出终点大于等于或小于等于 \(x\) 的数量。

注意，当 \(w_x = 0\) 时，观察员 \(x\) 能观察到的就是以 \(x\) 为起点的路径数量。

测试点 \(9 \sim 12\)

相当于所有路径的起点都是根节点。此时只有深度与 \(w\) 相等的观察员能观察到运动员，数量则是看其子树内有多少可能的终点。

测试点 \(13 \sim 16\)

相当于所有路径的终点都是根节点。若观察员 \(x\) 的深度为 \(d_x\)，则他能观察到的是起点 \(s\) 在 \(x\) 的子树内并且满足 \(d_s - d_x = w_x\) 的运动员。\(d_s - d_x = w_x\) 相当于 \(d_s = d_x + w_x\)，可利用桶的思想和子树差分求出满足条件的数量。

参考代码

#include <cstdio>
#include <vector>
#include <algorithm>
using std::swap;
using std::vector;
using std::sort;
using std::lower_bound;
using std::upper_bound;
const int N = 300005;
const int LOG = 19;
vector<int> tree[N];
int n, m, w[N],lca[N], d[N], s[N], t[N], ans[N];
namespace Chain {
    void solve() {
        vector<vector<int>> v; // v[i]表示以i为起点的路径有哪些终点
        v.resize(n + 1);
        for (int i = 1; i <= m; i++) {
            v[s[i]].push_back(t[i]); 
        }
        for (int i = 1; i <= n; i++) 
            sort(v[i].begin(), v[i].end());
        for (int i = 1; i <= n; i++) {
            if (w[i] == 0) {
                ans[i] = v[i].size(); continue;
            }
            int st = i - w[i];
            if (st >= 1) { // 起点等于i-w[i]，终点大于等于i的数量
                ans[i] += v[st].size() - (lower_bound(v[st].begin(), v[st].end(), i) - v[st].begin());
            }
            st = i + w[i];
            if (st <= n) { // 起点等于i+w[i]，终点小于等于i的数量
                ans[i] += (upper_bound(v[st].begin(), v[st].end(), i) - v[st].begin());
            }
        }
    }
};
namespace S1 {
    int cnt[N]; // cnt[i]表示以i为根的子树内有多少个终点
    void dfs(int u, int fa) {
        for (int v : tree[u]) {
            if (v == fa) continue;
            d[v] = d[u] + 1;
            dfs(v, u);       
            cnt[u] += cnt[v];
        }
        if (d[u] == w[u]) ans[u] = cnt[u];
    }
    void solve() {
        for (int i = 1; i <= m; i++) cnt[t[i]]++;
        dfs(1, 0);
    }
};
namespace T1 {
    int cnt[N * 2]; // cnt[i]作为d[起点]的计数桶
    vector<int> bg[N]; // bg[i]表示以i为起点的路径有哪些
    void dfs(int u, int fa) {
        int tmp = cnt[w[u] + d[u]];
        for (int v : tree[u]) {
            if (v == fa) continue;
            d[v] = d[u] + 1;
            dfs(v, u);
        }
        for (int i : bg[u]) cnt[d[s[i]]]++;
        ans[u] = cnt[w[u] + d[u]] - tmp;
    }
    void solve() {
        for (int i = 1; i <= m; i++) bg[s[i]].push_back(i);
        dfs(1, 0);
    }
};
namespace BF {
    int f[N][LOG];
    void dfs(int u, int fa) {
        for (int v : tree[u]) {
            if (v == fa) continue;
            f[v][0] = u; d[v] = d[u] + 1;
            dfs(v, u);
        }
    }
    int query(int x, int y) {
        if (d[x] < d[y]) swap(x, y);
        int delta = d[x] - d[y];
        for (int i = LOG - 1; i >= 0; i--)
            if (delta & (1 << i)) x = f[x][i];
        if (x == y) return x;
        for (int i = LOG - 1; i >= 0; i--)
            if (f[x][i] != f[y][i]) {
                x = f[x][i]; y = f[y][i];
            }
        return f[x][0];
    }
    void solve() {
        dfs(1, 0);
        for (int j = 1; j < LOG; j++)
            for (int i = 1; i <= n; i++)
                f[i][j] = f[f[i][j - 1]][j - 1];
        for (int i = 1; i <= m; i++) {
            int l = query(s[i], t[i]);
            int tm = 0, u = s[i];
            while (u != l) {
                if (tm == w[u]) ans[u]++;
                u = f[u][0];
                tm++;
            }
            if (tm == w[u]) ans[u]++;
            u = t[i]; tm = d[s[i]] + d[t[i]] - 2 * d[l];
            while (u != l) {
                if (tm == w[u]) ans[u]++;
                u = f[u][0];
                tm--;
            }
        }
    }
};
int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i < n; i++) {
        int s, t; scanf("%d%d", &s, &t);
        tree[s].push_back(t);
        tree[t].push_back(s);
    }    
    for (int i = 1; i <= n; i++) scanf("%d", &w[i]);
    for (int i = 1; i <= m; i++) scanf("%d%d", &s[i], &t[i]);
    if (n == 99994) { // 链
        Chain::solve();
    } else if (n == 99995) { // s=1
        S1::solve();
    } else if (n == 99996) { // t=1
        T1::solve();
    } else { // 暴力
        BF::solve();
    }
    for (int i = 1; i <= n; i++) printf("%d ", ans[i]);
    return 0;
}

测试点 \(17 \sim 20\)

考虑每条路径，分析路径对观察员的贡献。

一条路径可以分为上行部分和下行部分。设 \(d_i\) 表示点 \(i\) 在树上的深度。

对于路径的上行部分，\(d_s - d_x = w_x\) 的点会对观察员 \(x\) 产生贡献，即 \(d_s = w_x + d_x\)，并且这样的起点要在 \(x\) 的子树内。

对于路径的下行部分，\(d_s - d_{lca} + d_x - d_{lca} = w_x\) 的点会对观察员 \(x\) 产生贡献，即 \(d_s - 2 \times d_{lca} = w_x - d_x\)，并且这样的终点 \(t\) 要在 \(x\) 的子树内。

统计答案时就是统计满足上述表达式的路径数，所以可以用一个桶来统计相应的式子的每种取值有多少个，到达一个点时，把它作为起点和终点时相应式子取值的结果统计进桶里。

注意此时桶里并不是子树中的统计结果，而是 DFS 过程中之前经过的所有的点的，而此时想要求的是子树内的，这可以用回溯时的结果减去刚进入这个点时的结果，这个操作就是子树差分：在进入的时候先减，要回溯的时候再加回来即可。

另外，一条路径的贡献会在 \(s\) 和 \(t\) 的 \(lca\) 处消除，所以在回溯时还要把 \(lca\) 是这个点的路径的起点和终点相应的式子取值在桶里的计数减 \(1\)。

最后还有一点特殊情况，一条路径正好在其 \(lca\) 处产生了贡献，此时该路径的贡献会被算 \(2\) 次，因为它同时符合上行路径和下行路径的那个等式，所以如果对于某条路径而言 \(d_{s} - d_{lca} = w_{lca}\)，那就是在 \(lca\) 上有贡献，要减去其中 \(1\) 次重复的贡献。

可以用动态数组（STL vector）存储一个点会作为哪些路径的 \(s, t, lca\)。

参考代码

#include <cstdio>
#include <vector>
#include <algorithm>
using std::swap;
using std::vector;
const int N = 300005;
const int LOG = 19;
vector<int> tree[N], bg[N], ed[N], as_lca[N];
// d: 节点深度
int n, m, w[N], d[N], f[N][LOG], s[N], t[N], lca[N], ans[N];
// 上行、下行路径的贡献，w-d可能为负数，可以+n将其偏移，因此数组开两倍空间
int cnt_up[N * 2], cnt_down[N * 2]; 
void dfs(int u, int fa) {
    for (int v : tree[u]) {
        if (v == fa) continue;
        f[v][0] = u; d[v] = d[u] + 1;
        dfs(v, u);
    }
}
int query(int x, int y) {
    if (d[x] < d[y]) swap(x, y);
    int delta = d[x] - d[y];
    for (int i = LOG - 1; i >= 0; i--)
        if (delta & (1 << i)) x = f[x][i];
    if (x == y) return x;
    for (int i = LOG - 1; i >= 0; i--)
        if (f[x][i] != f[y][i]) {
            x = f[x][i]; y = f[y][i];
        }
    return f[x][0];
}
void calc(int u, int fa) {
    // 子树差分：进入的时候先减
    int tmp_up = cnt_up[w[u] + d[u]];
    int tmp_down = cnt_down[w[u] - d[u] + n];
    cnt_up[w[u] + d[u]] = cnt_down[w[u] - d[u] + n] = 0;

    for (int v : tree[u]) {
        if (v == fa) continue;
        calc(v, u);
    }  

    for (int i : bg[u]) cnt_up[d[s[i]]]++;
    for (int i : ed[u]) cnt_down[d[s[i]] - 2 * d[lca[i]] + n]++;

    ans[u] = cnt_up[w[u] + d[u]] + cnt_down[w[u] - d[u] + n];    

    // 一条路径的贡献会在lca处消除
    for (int i : as_lca[u]) {
        cnt_up[d[s[i]]]--;
        cnt_down[d[s[i]] - 2 * d[lca[i]] + n]--;
    }

    // 子树差分：回溯的时候加回来
    cnt_up[w[u] + d[u]] += tmp_up; 
    cnt_down[w[u] - d[u] + n] += tmp_down;
}
int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i < n; i++) {
        int s, t; scanf("%d%d", &s, &t);
        tree[s].push_back(t);
        tree[t].push_back(s);
    }
    dfs(1, 0);
    for (int j = 1; j < LOG; j++)
        for (int i = 1; i <= n; i++)
            f[i][j] = f[f[i][j - 1]][j - 1];
    for (int i = 1; i <= n; i++) scanf("%d", &w[i]);
    for (int i = 1; i <= m; i++) {
        scanf("%d%d", &s[i], &t[i]);
        lca[i] = query(s[i], t[i]);
        bg[s[i]].push_back(i);
        ed[t[i]].push_back(i);
        as_lca[lca[i]].push_back(i);
    }
    calc(1, 0);
    for (int i = 1; i <= m; i++) {
        // 上行路径和下行路径在lca处产生了重复贡献，减去一次
        if (d[s[i]] - d[lca[i]] == w[lca[i]]) ans[lca[i]]--;
    }  
    for (int i = 1; i <= n; i++) printf("%d ", ans[i]);
    return 0;
}

posted @ 2024-06-10 08:26 RonChen 阅读(328) 评论(0) 收藏举报

刷新页面返回顶部

RonChen

树上前缀和与差分

树上前缀和

例题：P4427 [BJOI2018] 求和

例题：P1084 [NOIP2012 提高组] 疫情控制

树上差分

点差分

例题：P3128 [USACO15DEC] Max Flow P

边差分

例题：P6869 [COCI2019-2020#5] Putovanje

例题：P2680 [NOIP2015 提高组] 运输计划

子树差分

例题：P3605 [USACO17JAN] Promotion Counting P

例题：P1600 [NOIP2016 提高组] 天天爱跑步

测试点 \(1 \sim 5\)

测试点 \(6 \sim 8\)

测试点 \(9 \sim 12\)

测试点 \(13 \sim 16\)

测试点 \(17 \sim 20\)

公告