递归与分治

递归

image

递归：直接或间接（A：这件事找 B；B：这件事找 A）地用到自己。

如何定义正整数？正整数是 \(1,2,3,\cdots\) 这些数。这个定义不是那么的“严密”，换一种方式：

  1. \(1\) 是正整数
  2. 如果 \(n\) 是正整数，\(n+1\) 也是正整数

这种定义就是递归式的：在“正整数”还没有定义时，就用到了“正整数”的定义。递归式定义能让定义简洁而严密。

例题：P5739 [深基7.例7] 计算阶乘

解题思路

原来学过循环求解，用一个 for 循环，就可以完成递推了。

参考代码 
#include <cstdio>
int main()
{
    int n; scanf("%d", &n);
    int ans = 1;
    for (int i = 1; i <= n; i++) ans *= i;
    printf("%d\n", ans);
    return 0;
}

数学函数也可以递归定义，阶乘函数 \(f(n)=n!\) 可以定义为：

\( \ f(n) = \begin{cases} 1 & \quad n=0 \\ f(n-1) \times n, &\quad n \ge 1\\ \end{cases} \ \)

参考代码 
#include <cstdio>
int f(int n) {
    return n == 0 ? 1 : f(n - 1) * n;
}
int main()
{
    int n; scanf("%d", &n);
    printf("%d\n", f(n));
    return 0;
}

要注意：一定要有个递归边界，要不然就无限递归了，另外递归过程中每一层的变量（包括参数）是独立的，互不影响。

例题：P5743 【深基7.习8】猴子吃桃

解题思路

可以循环递推，设 \(f_i\) 表示第 \(i\) 天时还剩多少桃子，则有 \(f_n = 1\)，\(f_i = (f_{i+1} + 1) \times 2\)，倒序循环即可，答案为 \(f_1\)。

也可以正着递推，设 \(f_i\) 表示在倒数第几天（或者说还剩几天）的时候还剩多少桃子，则有 \(f_1 = 1\)，\(f_i = (f_{i-1} + 1) \times 2\)，最后答案就是 \(f_n\)。

当然，这两种递推方式也可以写成递归形式，类似于上一题。

参考代码1 
#include <cstdio>
int n;
int calc(int x) {
    if (x == n) return 1;
    return 2 * (calc(x + 1) + 1);
}
int main()
{
    scanf("%d", &n);
    printf("%d\n", calc(1));
    return 0;
}
参考代码2 
#include <cstdio>
int calc(int x) {
    if (x == 1) return 1;
    return 2 * (calc(x - 1) + 1);
}
int main()
{
    int n;
    scanf("%d", &n);
    printf("%d\n", calc(n));
    return 0;
}

习题：B2142 求 1+2+3+...+N 的值

解题思路

与阶乘类似，\(1+2+ \cdots + n = (1 + 2 + \cdots + (n-1)) + n\)，因而若 \(f(n)\) 表示累加函数，则对于 \(n>0\) 时有 \(f(n)=f(n-1)+n\)。

#include <cstdio>
int f(int n) {
    return n == 0 ? 0 : f(n - 1) + n;
}
int main()
{
    int n; scanf("%d", &n);
    printf("%d\n", f(n));
    return 0;
}

选择题：ack 函数在输入参数 m = 2, n = 2 时的返回值为？

unsigned ack(unsigned m, unsigned n) {
    if (m == 0) return n + 1;
    if (n == 0) return ack(m - 1, 1);
    return ack(m - 1, ack(m, n - 1));
}
  • A. 5
  • B. 7
  • C. 9
  • D. 13
答案

这是一个经典的递归函数——阿克曼函数。

ack(2, 2) = ack(1, ack(2, 1))

现在，需要计算内层的 ack(2, 1) = ack(1, ack(2, 0))

接下来，计算更内层的 ack(2, 0) = ack(1, 1)

继续计算 ack(1, 1) = ack(0, ack(1, 0))

继续计算 ack(1, 0) = ack(0, 1) = 1 + 1 = 2

开始将结果代回，ack(1, 1) = ack(0, ack(1, 0)) = ack(0, 2) = 2 + 1 = 3

所以有 ack(2, 0) = ack(1, 1) = 3

接下来计算 ack(1, 3) = ack(0, ack(1, 2))，ack(1, 2) = ack(0, ack(1, 1)) = ack(0, 3) = 3 + 1 = 4，所以 ack(1, 3) = ack(0, 4) = 4 + 1 = 5

所以有 ack(2, 1) = ack(1, 3) = 5

最后计算 ack(1, 5) = ack(0, ack(1, 4))，ack(1, 4) 等于 ack(0, ack(1, 3))，已经计算出 ack(1, 3) = 5，所以 ack(1, 4) = ack(0, 5) = 5 + 1 = 6

将 ack(1, 4) = 6 代回，ack(1, 5) 等于 ack(0, 6) = 6 + 1 = 7

B

递归与递推

对于前面的问题，用递归和递推都解决了，那么两者有什么区别？

运行下面两份代码，输入 \(40\)，比较运行效率：

#include <cstdio>
int f[45];
int main()
{
	int n; scanf("%d", &n);
	f[1] = 1; f[2] = 1;
	for (int i = 3; i <= n; i++) f[i] = f[i - 1] + f[i - 2];
	printf("%d\n", f[n]);
	return 0;
}

循环递推，时间复杂度 \(O(n)\)。

#include <cstdio>
int f(int x) {
	if (x <= 2) return 1;
	return f(x - 1) + f(x - 2);
}
int main()
{
	int n; scanf("%d", &n);
	printf("%d\n", f(n));
	return 0;
}

递归，时间复杂度 \(O(fib(n))\)，同一项会多次计算，每次都递归到 f(1) 或 f(2) 返回。

要提升递归的效率，可以使用记忆化（用数组标记每一项是否已经算出，已经算出就直接返回）的方法，不过一定要确定真的不需要重复计算才行。

#include <cstdio>
int ans[45];
bool vis[45];
int f(int x) {
	if (x <= 2) return 1;
	if (vis[x]) return ans[x];
	vis[x] = true;
	return ans[x] = f(x - 1) + f(x - 2);
}
int main()
{
	int n; scanf("%d", &n);
	printf("%d\n", f(n));
	return 0;
}

时间复杂度 \(O(n)\)，每项只算一次，算每项时是 \(O(1)\) 的。

通常建议简单递推式使用循环递推实现。

使用递归往往适用于如下情况：

  1. 难以找到循环的合适顺序时（递推式中出现的下标可能变大也可能变小）
  2. 从要求的第 \(n\) 项出发，有用的项很少（比如 \(f_n = f_{n/2} + f_{n/3}\)）

选择题：斐波那契数列的定义为：\(F_1 = 1\)，\(F_2 = 1\)，\(F_n = F_{n-1} + F_{n-2} (n \ge 3)\)。现在用如下程序来计算斐波那契数列的第 \(n\) 项，其时间复杂度为？

F(n):
    if n<=2 return 1
    else return F(n-1) + F(n-2)
  • A. \(O(n)\)
  • B. \(O(n^2)\)
  • C. \(O(2^n)\)
  • D. \(O(n \log n)\)
答案

C。

令 \(T(n)\) 表示计算 \(F(n)\) 所需的时间。根据代码 return F(n-1) + F(n-2)，为了计算 F(n)，程序需要先计算 F(n-1) 和 F(n-2)，然后将它们相加。因此，\(T(n)\) 可以表示为 \(T(n) = T(n-1) + T(n-2) + O(1)\)，其中 \(O(1)\) 代表加法操作的常数时间。这个递推关系与斐波那契数列本身的定义非常相似。

对于 \(T(n) = T(n-1) + T(n-2)\) 而言，可以进行估算：

  • 上限：\(T(n) \lt 2 T(n-1) \lt 4 T(n-2) \lt \cdots \lt 2^n T(0)\)，所以 \(T(n)\) 的一个上限是 \(O(2^n)\)。
  • 下限：\(T(n) \gt 2 T(n-2) \gt 4 T(n-4) \gt \cdots \gt 2^{n/2} T(0)\)，所以 \(T(n)\) 的一个下限是 \(O(2^{n/2})\)。

实际上，这个更紧的界大约是 \(O(1.618^n)\)，其中 1.618 是黄金分割数。

在实际编程时，如果使用递推计算或是记忆化的方法，其时间复杂度可以优化到 \(O(n)\)。

例题：P1464 Function

解题思路

使用记忆化的方法就可以避免超时了，有效状态数是 \(20 \times 20 \times 20\) 级别，计算加法的时间复杂度是 \(O(1)\)，算下来只需要做 \(8000\) 这个量级的计算量，完全不用担心超时。

不过需要注意当 \(a \le 0\) 或 \(b \le 0\) 或 \(c \le 0\) 或 \(a>20\) 或 \(b>20\) 或 \(c>20\) 时可以不把答案记进数组，避免数组访问越界。

参考代码 
#include <cstdio>
using ll = long long;
const int N = 25;
bool vis[N][N][N]; // 记录某状态是否被计算过 
ll ans[N][N][N]; // 记录某状态下的计算结果
ll w(ll a, ll b, ll c) {
    if (a <= 0 || b <= 0 || c <= 0) return 1;
    if (a > 20 || b > 20 || c > 20) return w(20, 20, 20);
    if (vis[a][b][c]) return ans[a][b][c]; // 如果曾经计算过可以直接返回存下来的结果
    // 需要展开计算则在计算完成后更新相应状态及计算结果
    if (a < b && b < c) {
        ans[a][b][c] = w(a, b, c-1) + w(a, b-1, c-1) - w(a, b-1, c);
        vis[a][b][c] = true;
        return ans[a][b][c];
    }
    ans[a][b][c] = w(a-1, b, c) + w(a-1, b-1, c) + w(a-1, b, c-1) - w(a-1, b-1, c-1);
    vis[a][b][c] = true;
    return ans[a][b][c];
}
int main()
{
    while (true) {
        ll a, b, c; scanf("%lld%lld%lld", &a, &b, &c);
        if (a == -1 && b == -1 && c == -1) break;
        printf("w(%lld, %lld, %lld) = %lld\n", a, b, c, w(a, b, c));
    }
    return 0;
}

例题：P1028 [NOIP 2001 普及组] 数的计算

解题思路

可以定义一个函数 int f(int n) 表示当最后一个拼上的数是 \(n\) 的时候，最终能生成多少个数列。

在计算时，首先设答案（返回值）是 \(1\)（表示第一种情况），然后循环枚举拼接的数 \(i\)（需满足 \(2i \le x\)），把 f(i) 的结果加进当前返回值，循环结束后返回结果。

为了保证不重复计算，需要加上记忆化。

一共 \(n\) 项要算，算一项的时候有 \(n/2\) 次循环，所以时间复杂度为 \(O(n^2)\)。

参考代码 
#include <cstdio>
const int N = 1005;
int f[N];
int solve(int n) {
    if (n == 1) return 1;
    if (f[n] != 0) return f[n];
    int res = 1;
    for (int i = 1; i * 2 <= n; i++) res += solve(i);
    return f[n] = res;
}
int main()
{
    int n; scanf("%d", &n);
    printf("%d\n", solve(n));
    return 0;
}

例题：P1928 外星密码

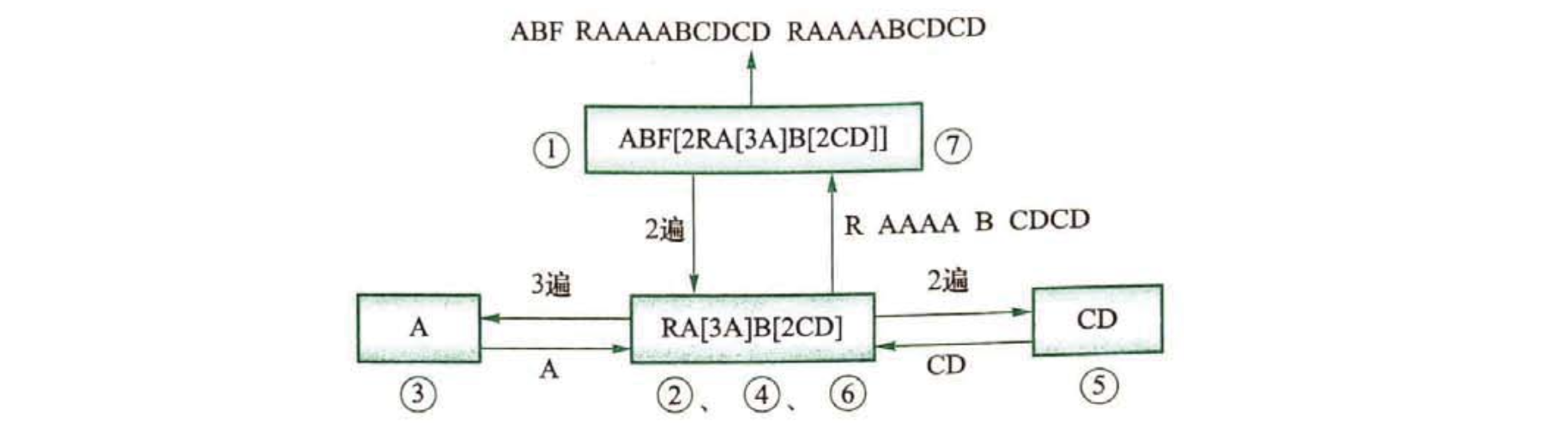
分析：如果只有一层方括号，那么只需要找到方括号，就可以提取出重复次数，然后将重复部分按次数复制若干份拼接起来即可。如果方括号的“重复部分”里还有方括号呢？用同样的方式展开即可。可以发现，这个机制和递归非常吻合，因此本题适合用递归的方式来实现。

image

参考代码 
#include <cstdio>
#include <iostream>
#include <string>
#include <stack>
using namespace std;
const int N = 20005;
int match[N]; // match[i]代表code[i]为左括号时对应的右括号的下标
/**
 * @brief 递归解压缩函数
 * @param code 完整的原始密码字符串
 * @param l 当前要解压的子串的左边界（包含）
 * @param r 当前要解压的子串的右边界（不包含）
 * @return 解压后的字符串
 */
string decompress(string &code, int l, int r) {
    // 解压缩 code[l]~code[r-1]
    int i = l;
    int num = 0; // 用于累积当前层级的重复次数
    string res; // 用于存储当前层级解压出的基本字符串（重复前）
    // 遍历当前需要处理的子串 code[l...r-1]
    while (i < r) {
        if (code[i] == '[') {
            // 遇到左括号，说明有一个嵌套的压缩块
            // 递归调用 decompress 来处理这个内部块
            // 内部块的范围是 [i+1, match[i]-1]
            res += decompress(code, i + 1, match[i]);
            // 处理完内部块后，直接跳到右括号的下一个位置
            i = match[i] + 1;
        } else {
            // 处理非括号的字符
            if (code[i] >= '0' && code[i] <= '9') {
                // 如果是数字，累加到重复次数 num 中
                num = num * 10 + (code[i] - '0');
            } else {
                // 如果是字母，直接追加到结果字符串中
                res += code[i];
            } 
            i++; // 继续处理下一个字符
        }
    }
    // 如果整个块内没有数字，则默认重复1次
    if (num == 0) num = 1;
    string ret; // 最终要返回的、重复后的字符串
    // 将解压出的基本字符串 res 重复 num 次
    for (int i = 1; i <= num; i++) ret += res;
    return ret;
}
int main()
{
    string code;
    cin >> code; // 读取完整的密码字符串
    // 预处理：使用栈来匹配所有的括号
    stack<int> s;
    for (int i = 0; i < code.size(); i++) {
        if (code[i] == '[') {
            // 遇到左括号，将其下标入栈
            s.push(i);
        } else if (code[i] == ']') {
            // 遇到右括号，栈顶的元素就是与之匹配的左括号的下标
            match[s.top()] = i;
            s.pop(); // 匹配完成，出栈
        }
    }
    // 调用递归函数，从整个字符串的范围 [0, code.size()) 开始解压
    cout << decompress(code, 0, code.size()) << "\n";
    return 0;
}

如果能将一个大的任务分解成若干规模较小的任务，而且这些任务的形式与结构和原问题一致，就可以考虑使用递归。当问题规模足够小或者达到了边界条件就要停止递归。分解完问题后还要将这些规模小的任务的处理结果合并，最后逐级上报，解决最大规模的问题。

递归与栈的关系

栈是一种“后进先出”的数据结构，而函数调用自身，会形成一个调用链。当递归到达最深层（基本情况）后，会开始逐层返回。这个“逐层返回”的顺序，正好与“逐层调用”的顺序相反。最后调用的函数最先返回，最先调用的函数最后返回。这种行为模式与栈的“后进先出”特性完全吻合。

函数调用栈

当在代码中调用一个函数时，操作系统会为这个函数在内存中创建一个“栈帧”（Stack Frame），这个栈帧被推入一个叫作“函数调用栈”（Call Stack）的特殊栈中。

这个栈帧里存储了关于这次函数调用的所有重要信息，包括：

  • 函数的参数（Parameters）
  • 函数的局部变量（Local Variables）
  • 返回地址（Return Address）：即函数执行完毕后，程序应该回到哪里继续执行。

联系与引申

栈溢出（Stack Overflow）：如果递归没有正确的“基本情况”来终止，或者递归的深度太深，调用栈会持续增长，直到耗尽所有分配给它的内存空间，从而导致程序崩溃，这就是著名的“栈溢出”错误。

递归转迭代：任何一个递归算法，都可以被转换成一个非递归的、使用循环和显式栈（即自己创建和管理的栈数据结构）的等价算法。在某些情况下，这样做可以避免函数调用的开销，提高效率，或者避免栈溢出。

选择题：在程序运行过程中，如果递归调用的层数过多，可能会由于什么引发错误？

  • A. 系统分配的栈空间溢出
  • B. 系统分配的队列空间溢出
  • C. 系统分配的链表空间溢出
  • D. 系统分配的堆空间溢出
答案

A。

每次函数调用（包括递归调用）时，系统都会在内存的栈区域中为该次调用分配一块空间（称为“栈帧”），用于存储函数的参数、局部变量、返回地址等信息。当函数执行完毕返回时，这块空间会被释放。

如果递归调用的层次非常深，就会连续不断地在栈上分配空间，而没有机会释放。由于系统分配给程序的栈空间是有限的，当占用的栈空间超出了这个限制时，就会发生“栈溢出”错误，导致程序异常终止。

选择题：在 C++ 中，以下哪个函数调用会造成栈溢出？

  • A. int foo() { return 0; }
  • B. int bar() { int x = 1; return x; }
  • C. void baz() { int a[1000]; baz(); }
  • D. void qux() { return; }
答案

C。这个函数会导致栈溢出，原因有两个关键点：

  1. 无限递归：函数 baz() 在没有设置任何终止条件的情况下直接调用了自身。
  2. 栈上分配：每次调用 baz() 时，它都会在栈上创建一个包含 1000 个整数的数组 a。

每次 baz() 调用自身，一个新的“栈帧”就会被推入调用栈。这个栈帧里包含了数组 a 所需的内存（在大多数系统中大约是 4KB 左右）以及函数的返回地址等信息。由于递归永不停止，调用栈会持续增长，直到耗尽所有分配给它的有限内存空间，最终导致程序因“栈溢出”错误而崩溃。

分治

如果想知道我国的人口数量，就需要进行人口普查。让每一个省份都去统计本省有多少人，然后将各省人口累加起来，就可以获得全国的人口数量。而要想知道某一个省的人口数量，可以让省里的每一个城市统计本市有多少人，然后将各市人口累加起来，就可以获得这个省的人口数量……以此类推，层层细分，最后统计一个村子或者一个小区有多少人，这个任务就足够简单了。把一个复杂的问题细分成若干结构相同但规模更小的子问题，然后将每个子问题的解合并起来，就得到了复杂问题的解，这就是分治策略。

P5461 赦免战俘

#include <cstdio>
const int N = 1050;
int a[N][N];
// 左上角坐标(x,y)，边长为len的正方形
void solve(int x, int y, int len) {
	// 先考虑边界条件
	if (len==1) {
		a[x][y]=1;
		return;
	} 
	// 拆分问题
	// 左上角全为0（相当于不用处理）
	// 继续用同样的方式处理右上，左下，右下
	solve(x,y+len/2,len/2);
	solve(x+len/2,y,len/2);
	solve(x+len/2,y+len/2,len/2);
}
int main()
{
	int n; scanf("%d",&n);
	// n = (1<<n);
	int len=1;
	for (int i=1;i<=n;i++) len*=2;
	solve(1,1,len);
	for (int i=1;i<=len;i++) {
		for (int j=1;j<=len;j++) {
			printf("%d ",a[i][j]);
		}
		printf("\n");
	}
    return 0;
}

P1228 地毯填补问题

#include <cstdio>
int px, py;
int judge(int xx, int yy, int x, int y, int n) { // 判断残缺的块在哪个分区
    if (xx < x + n / 2) return yy < y + n / 2 ? 1 : 2; // 左上/右上
    return yy < y + n / 2 ? 3 : 4; // 左下/右下
}
void solve(int n, int x, int y, int miss, int xx, int yy) {
    if (n == 1) return;
    n = n / 2;
    if (miss == 1) {
        printf("%d %d %d\n", x + n, y + n, 1);
        solve(n, x, y, judge(xx, yy, x, y, n), xx, yy);
        solve(n, x, y + n, 3, x + n - 1, y + n);
        solve(n, x + n, y, 2, x + n, y + n - 1);
        solve(n, x + n, y + n, 1, x + n, y + n);
    } else if (miss == 2) {
        printf("%d %d %d\n", x + n, y + n - 1, 2);
        solve(n, x, y, 4, x + n - 1, y + n - 1);
        solve(n, x, y + n, judge(xx, yy, x, y + n, n), xx, yy);
        solve(n, x + n, y, 2, x + n, y + n - 1);
        solve(n, x + n, y + n, 1, x + n, y + n);
    } else if (miss == 3) {
        printf("%d %d %d\n", x + n - 1, y + n, 3);
        solve(n, x, y, 4, x + n - 1, y + n - 1);
        solve(n, x, y + n, 3, x + n - 1, y + n);
        solve(n, x + n, y, judge(xx, yy, x + n, y, n), xx, yy);
        solve(n, x + n, y + n, 1, x + n, y + n);
    } else { 
        printf("%d %d %d\n", x + n - 1, y + n - 1, 4);
        solve(n, x, y, 4, x + n - 1, y + n - 1);
        solve(n, x, y + n, 3, x + n - 1, y + n);
        solve(n, x + n, y, 2, x + n, y + n - 1);
        solve(n, x + n, y + n, judge(xx, yy, x + n, y + n, n), xx, yy);
    }
}
int main()
{
    int k;
    scanf("%d%d%d", &k, &px, &py);
    int len = 1;
    for (int i = 1; i <= k; i++) len *= 2;
    solve(len, 1, 1, judge(px, py, 1, 1, len), px, py);
    return 0;
}

归并排序

例题：P1177 【模板】排序

介绍一种新的排序算法——归并排序。要理解归并排序，首先要理解归并。考虑这样一个问题：给定两个有序的序列 \(a,b\)，把两个序列合并成一个序列，使得合并出的这个序列是有序的。

算法的过程很简单，维护两个位置 \(i\) 和 \(j\)，代表当前考虑 \(a\) 数组的第 \(i\) 个元素与 \(b\) 数组的第 \(j\) 个元素。如果 \(a_i \le b_j\)，则在答案数组添加一个 \(a_i\)，同时 \(i\) 向后移动。如果 \(a_i > b_j\)，则在答案数组添加一个 \(b_j\)，同时 \(j\) 向后移动。注意到，如果 \(a,b\) 两个数组中有一个被合并完了，可以直接把另一个数组剩下的部分接到答案数组最后面。

比如有两个有序数组 \(a=[1,3,7,8], b=[2,4,6,9]\)，对这两个数组进行归并：

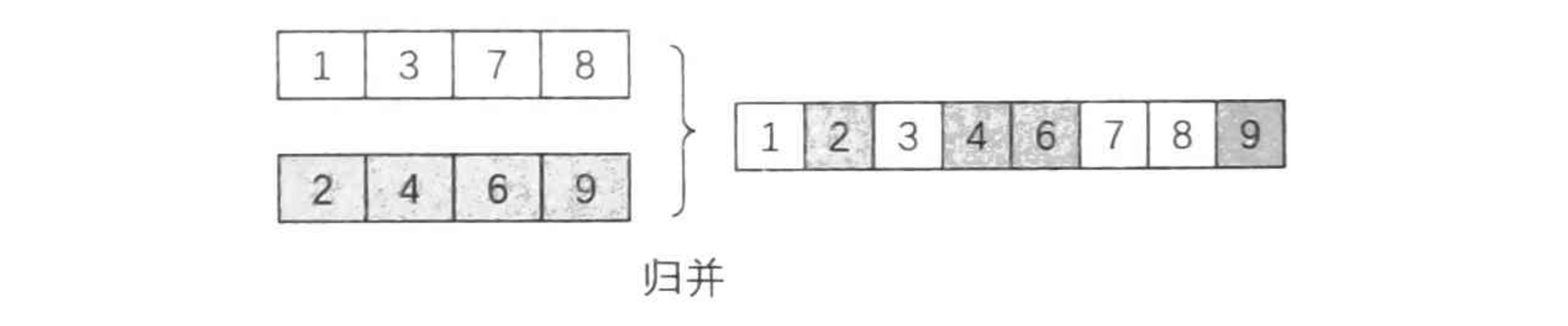
image

有了归并算法之后，要对一个长度为 \(n\) 的序列进行排序，可以考虑采用分治的思想来解决：如果 \(n=1\)，这个序列自然是有序的，所以不用进行排序——这就是可以直接解决的子问题。否则，将序列分为两个长 \(\frac{n}{2}\) 的子序列，对这两个子序列分别递归地进行排序——这是把一个复杂的问题转换为若干个简单一些的问题，然后递归下去解决这些更简答的问题。

当两个子序列有序后，对这两个子序列进行归并，使当前这个长度为 \(n\) 的序列有序——这就是当每个子问题都处理完之后，合并子问题的答案得到原问题的答案。

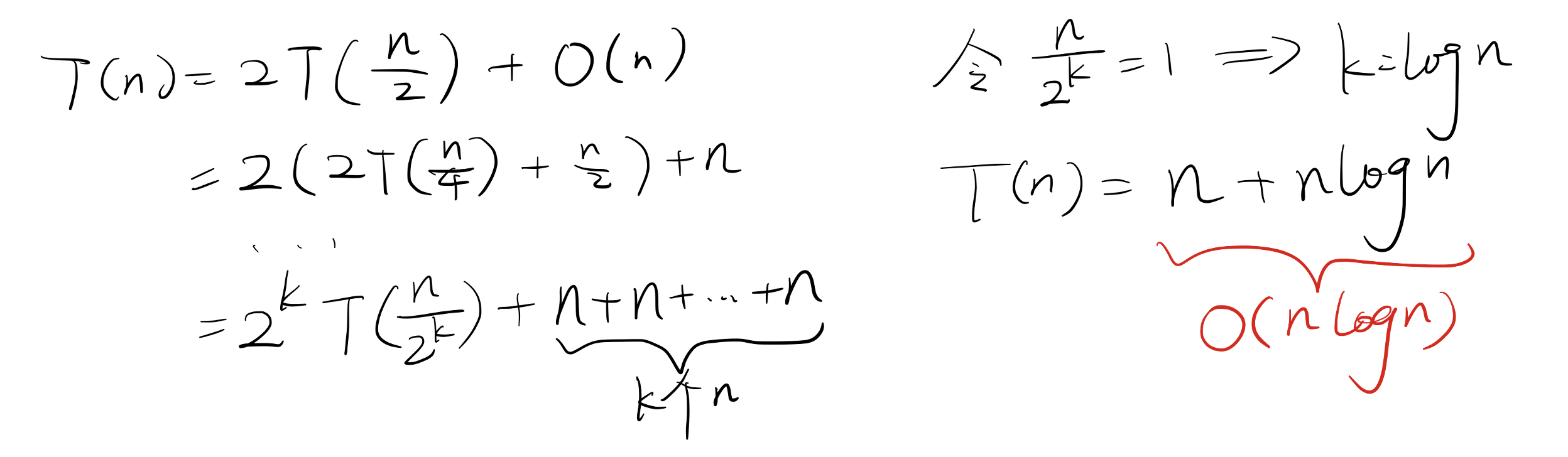
归并排序的时间复杂度为 \(T(n)=2T(\frac{n}{2})+O(n)=O(n \log n)\)。

推导

image

#include <cstdio>
const int N = 1e5 + 5;
int a[N], tmp[N]; // tmp是合并时用的临时数组
void mergesort(int l, int r) { // 实现对a[l]~a[r]完成排序
	if (l==r) { // 只剩一个数，无需排序，直接返回
		return;
	}
	int mid=(l+r)/2; // a[l]~a[mid]   a[mid+1]~a[r]
	mergesort(l,mid); mergesort(mid+1,r); // 递归到更小的子问题
	// 上面这两个递归调用返回之后意味着左半边和右半边内部已经有序
	// 接下来要解决合并的问题
	// a[l]~a[mid]    a[mid+1]~a[r]
	// 先合并到 tmp[l]~tmp[r]
	// 最后再搬回 a
	int i=l, j=mid+1; // 两部分的合并进度
	int k=l; // 下一个数据合并到tmp的什么位置
	while (i<=mid && j<=r) {
		if (a[i] <= a[j]) {
			tmp[k]=a[i]; i++;
		} else {
			tmp[k]=a[j]; j++;
		}
		k++;
	}
	// 上面循环结束时必然是左右半区的其中一个已经合并完成
	// 另一个必然还剩下最后一段没有合并进去
	while (i<=mid) {
		tmp[k]=a[i]; i++; k++;
	}
	while (j<=r) {
		tmp[k]=a[j]; j++; k++;
	}
	// 此时tmp[l]~tmp[r]已经合并完成，搬回原数组a
	for (int i=l;i<=r;i++) a[i]=tmp[i];
}
int main()
{
	int n; scanf("%d",&n);
	for (int i=1;i<=n;i++) scanf("%d",&a[i]);
	mergesort(1,n);
	for (int i=1;i<=n;i++) printf("%d ",a[i]);
    return 0;
}

递归版的归并排序是“自顶向下的”：它先把一个大数组不断地对半切分，直到每个子数组只剩一个元素（天然有序），然后再一层一层地把这些有序的子数组合并起来。

非递归版（自底向上）则完全相反。它放弃了递归的“切分”过程，直接从“合并”开始。

想象一下，任何单个元素本身都是一个有序的“子数组”。非递归归并排序的思路就是：

  1. 第一轮：将数组中相邻的** 1 个元素和 1 个元素**进行合并，形成若干个长度为 2 的有序子数组。
  2. 第二轮：将数组中相邻的长度为 2 的有序子数组进行合并，形成若干个长度为 4 的有序子数组。
  3. 第三轮：将数组中相邻的长度为 4 的有序子数组进行合并，形成若干个长度为 8 的有序子数组。
  4. ...以此类推，每一轮都将上一轮合并好的、更长的有序子数组进行两两合并，直到整个数组合并成一个，排序完成。

这个过程就像从最小的砖块（单个元素）开始，一步一步搭建成一堵有序的墙（整个数组），所以被称为“自底向上”。

算法步骤

整个算法由两个嵌套的循环控制：

  1. 外层循环：控制每次要合并的子数组的长度 sub_len。这个长度从 1 开始，每次循环后翻倍（sub_len = 1, 2, 4, 8, ...）。
  2. 内存循环：根据当前的 sub_len，遍历整个数组，对所有相邻的、长度为 sub_len 的子数组进行两两合并。
    • 例如，当 sub_len = 1 时，它合并 arr[0] 和 arr[1]，然后合并 arr[2] 和 arr[3]，以此类推。
    • 当 sub_len = 2 时，它合并 arr[0...1] 和 arr[2...3]，然后合并 arr[4...5] 和 arr[6...7]，以此类推。

假设有数组 [8, 3, 6, 4, 9, 2, 7, 5]。

第 1 轮（sub_len = 1）：合并长度为 1 的子数组

  • 合并 [8] 和 [3]，得到 [3, 8]
  • 合并 [6] 和 [4]，得到 [4, 6]
  • 合并 [9] 和 [2]，得到 [2, 9]
  • 合并 [7] 和 [5]，得到 [5, 7]
    数组变为：[3, 8, 4, 6, 2, 9, 5, 7]

第 2 轮（sub_len = 2）：合并长度为 2 的有序子数组

  • 合并 [3, 8] 和 [4, 6]，得到 [3, 4, 6, 8]
  • 合并 [2, 9] 和 [5, 7]，得到 [2, 5, 7, 9]
    数组变为：[3, 4, 6, 8, 2, 5, 7, 9]

第 3 轮（sub_len = 4）：合并长度为 4 的有序子数组

  • 合并 [3, 4, 6, 8] 和 [2, 5, 7, 9]，得到 [2, 3, 4, 5, 6, 7, 8, 9]
    数组变为：[2, 3, 4, 5, 6, 7, 8, 9]

此时 sub_len 变为 8，大于等于数组长度，循环结束。排序完成。

关键点：处理边界情况。当数组长度不是 2 的幂时，最后一组可能不完整（只有一个子数组，或者第二个子数组比 sub_len 短），代码需要能正确处理这种情况。

参考代码 
#include <cstdio>
#include <vector>
#include <algorithm>
using std::vector;
using std::min;
/**
 * @brief 归并两个有序子数组 arr[left...mid] 和 arr[mid+1...right]
 * 
 * @param arr 待排序的数组
 * @param left 左子数组的起始索引
 * @param mid 左子数组的结束索引
 * @param right 右子数组的结束索引
 */
void merge(vector<int> &arr, int left, int mid, int right) {
    // 创建一个临时数组来存储归并后的结果
    vector<int> temp(right - left + 1);
    int i = left;       // 左子数组的指针
    int j = mid + 1;    // 右子数组的指针
    int k = 0;          // 临时数组的指针
    // 当两个子数组都还有元素时，比较并放入临时数组
    while (i <= mid && j <= right) {
        if (arr[i] <= arr[j]) {
            temp[k++] = arr[i++];
        } else {
            temp[k++] = arr[j++];
        }
    }
    // 如果左子数组还有剩余元素，全部复制到临时数组
    while (i <= mid) {
        temp[k++] = arr[i++];
    }
    // 如果右子数组还有剩余元素，全部复制到临时数组
    while (j <= right) {
        temp[k++] = arr[j++];
    }
    // 将排序好的临时数组内容复制回原数组的对应位置
    for (int l = 0; l < temp.size(); l++) {
        arr[left + l] = temp[l];
    }
}
void mergeSortIterative(vector<int> &arr) {
    int n = arr.size();
    if (n <= 1) return; // 数组为空或只有一个元素，无需排序
    for (int sub_len = 1; sub_len < n; sub_len *= 2) { // 外层循环：控制每次合并的子数组长度(1, 2, 4, 8, ...)
        // 内层循环：遍历数组，找到需要合并的左右子数组对
        for (int left_start = 0; left_start < n - 1; left_start += 2 * sub_len) {
            // 计算左子数组的结束位置
            int mid = min(left_start + sub_len - 1, n - 1);
            // 计算右子数组的结束位置
            int right_end = min(left_start + 2 * sub_len - 1, n - 1);
            // 调用归并函数，合并 arr[left_start...mid] 和 arr[mid+1...right_end]
            // 注意：如果右子数组不存在（mid >= right_end），则不会发生合并
            if (mid < right_end) {
                merge(arr, left_start, mid, right_end);
            }
        }
    }
}
int main()
{
    int n; scanf("%d", &n);
    vector<int> a(n);
    for (int i = 0; i < n; i++) scanf("%d", &a[i]);
    mergeSortIterative(a);
    for (int i = 0; i < n; i++) {
        printf("%d%c", a[i], i == n - 1 ? '\n' : ' ');
    }
    return 0;
}

归并排序算法是由伟大的数学家和计算机科学家约翰·冯·诺依曼（John Von Neumann）发明的。

他在 1945 年首次提出了这个算法。当时，冯·诺依曼正在参与早起电子计算机 EDVAC 的设计工作，归并排序是他为这台计算机设想的排序程序的一部分。

冯·诺依曼的这一发明在计算机科学史上具有里程碑式的意义，因为：

  • 它是最早为电子计算机设计的算法之一。
  • 它的时间复杂度稳定在 \(O(n \log n)\)，在最坏情况下也表现优异。
  • 它为后来的许多算法设计（尤其是基于分治思想的算法）提供了重要的启示。

选择题：设 A 和 B 是两个长度为 n 的有序数组，现在需要将 A 和 B 合并成一个排好序的数组，问任何以元素比较作为基本运算的归并算法，在最坏情况下至少要做多少次比较？

  • A. \(n^2\)
  • B. \(n \log n\)
  • C. \(2n\)
  • D. \(2n-1\)
答案

D。

回顾归并的算法流程，每进行一次比较，就会有一个元素被确定并放入结果数组。

最好情况

假设数组 A 的所有元素都小于数组 B 的所有元素（例如 A = {1,2,3}, B = {4,5,6}）。算法会先将 A 的所有元素逐一与 B 的第一个元素比较。在 n 次比较之后，A 数组的所有元素都被放入结果数组中，A 数组被耗尽。此时，B 数组的所有元素将直接被复制到结果数组的末尾，不再需要任何比较。因此，最好情况下的比较次数是 n 次。

最坏情况

为了让比较次数最多，需要让“其中一个数组被耗尽”的过程尽可能晚。所以，最坏情况发生在两个数组的元素被交替选入结果数组中，直到最后一刻才有一个数组被耗尽。构造一个最坏的例子，A = {1,3,5,...}, B = {2,4,6,...}。在合并过程中，A 的第一个元素和 B 的第一个元素比较，A 的第二个元素和 B 的第一个元素比较，A 的第二个元素和 B 的第二个元素比较，……，两个数组的指针会交替前进。这个比较过程会一直持续，直到结果数组中已经放入了 2n-1 个元素。此时，只剩下最后一个元素（它必然是所有元素中最大的），它无需再比较，直接放入结果数组的末尾即可。因为每放入一个元素（除了最后一个）都需要一次比较，所以放入 2n-1 个元素就需要 2n-1 次比较。

例题：P1908 逆序对

对于给定的一段正整数序列 \(a\)，逆序对是序列中 \(a_i>a_j\) 且 \(i<j\) 的有序对。求一个长度为 \(n\) 的序列的逆序对个数，其中 \(1 \le n \le 5 \times 10^5\)。

分析：对于这个问题，可以在归并排序的过程中同时求出序列的逆序对数。

如果 \(n=1\)，这个序列的逆序对个数自然是 \(0\)——这就是可以直接解决的子问题。否则，将序列分为两个长度为 \(\frac{n}{2}\) 的子序列，对这两个子序列分别递归地求出其内部的逆序对——这是把一个复杂的问题转换为若干个简单一些的问题，然后递归下去解决简单一些的问题。

当递归计算了两个子序列内部的逆序对数后，考虑怎么合并这两个子序列。可以发现逆序对还有一种来源，前一个序列中某个元素和后一个序列中某个元素所构成的逆序对，因此还要计算这部分的个数——这就是当每个子问题都处理完之后，合并子问题的答案得到原问题的答案。

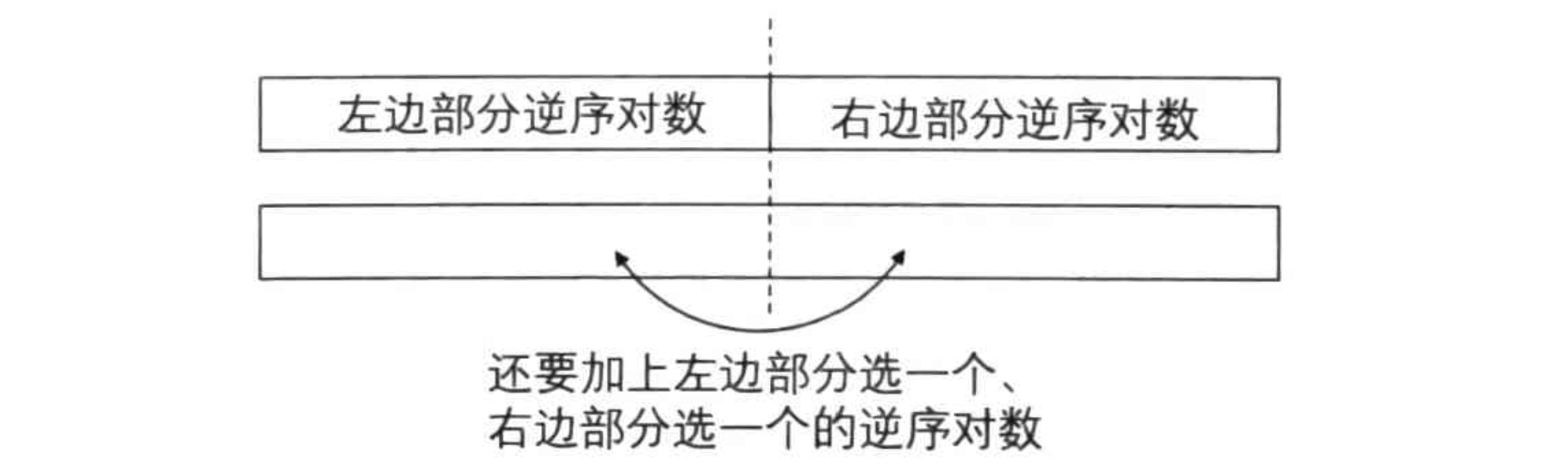
image

那么如何算这种一前一后的情况呢？由于在序列位置中，前一个子序列中的元素一定在后一个子序列中的元素的前面，所以逆序对的 \(i<j\) 已经自然满足了，只需要再考虑 \(a_i>a_j\)。

回顾归并排序的归并过程。对两个有序数组 \(a\) 和 \(b\) 归并的时候，如果某次比较之后在答案数组中放入的元素是 \(b_j\)，而和 \(b_j\) 做比较的元素是 \(a_i\)，那么一定有 \(a_i, a_{i+1}, \dots\) 均比 \(b_j\) 大，所以在归并排序的过程中，每当在答案数组中放入 \(b_j\) 时，会产生一批逆序对，这样就可以边归并排序边求出整个序列的逆序对数了。

时间复杂度和归并排序一样，为 \(O(n \log n)\)。

#include <cstdio>
using ll = long long;
const int N = 5e5 + 5;
int a[N], tmp[N]; // tmp是合并时用的临时数组
ll mergesort(int l, int r) { // 实现对a[l]~a[r]完成排序
	if (l==r) { // 只剩一个数，无需排序
		return 0;
	}
	int mid=(l+r)/2; // a[l]~a[mid]   a[mid+1]~a[r]
	ll sum=0;
	sum += mergesort(l,mid); 
	sum += mergesort(mid+1,r);
	// 上面这两个递归调用返回之后意味着左半边和右半边内部已经有序
	// 接下来要解决合并的问题
	// a[l]~a[mid]    a[mid+1]~a[r]
	// 先合并到 tmp[l]~tmp[r]
	// 最后再搬回 a
	int i=l, j=mid+1; // 两部分的合并进度
	int k=l; // 下一个数据合并到tmp的什么位置
	while (i<=mid && j<=r) {
		if (a[i]<=a[j]) { // a[i]<=a[j]说明这次合并取左边的数
			tmp[k]=a[i]; i++;
		} else { // a[i]>a[j] 取右边的数
			// (a[i],a[j]) 构成了逆序对
			// (a[i+1,...mid],a[j]) 都构成了逆序对
			sum+=(mid-i+1);
			tmp[k]=a[j]; j++;
		}
		k++;
	}
	// 上面循环结束时必然是左右半区的其中一个已经合并完成
	// 另一个必然还剩下最后一段没有合并进去
	while (i<=mid) {
		tmp[k]=a[i]; i++; k++;
	}
	while (j<=r) {
		tmp[k]=a[j]; j++; k++;
	}
	// 此时tmp[l]~tmp[r]已经合并完成，搬回原数组a
	for (int i=l;i<=r;i++) a[i]=tmp[i];
	return sum;
}
int main()
{
	int n; scanf("%d",&n);
	for (int i=1;i<=n;i++) scanf("%d",&a[i]);
	ll ans=mergesort(1,n);
	printf("%lld\n",ans);
    return 0;
}

快速排序

快速排序（Quick Sort）是计算机科学中最著名、应用最广泛的排序算法之一。它的核心思想是分治（Divide and Conquer），这个策略可以分为三个步骤：

  1. 分解（Divide）：
    • 从待排序的数组中，挑选一个元素作为“基准”（Pivot）。
    • 围绕这个基准，对数组进行“分区”（Partition）操作。分区操作完成后，数组会变成三个部分：
      1. 一个所有元素都小于基准的子数组。
      2. 基准元素本身（它现在已经位于其最终排好序的位置）。
      3. 一个所有元素都大于或等于基准的子数组。
  2. 解决（Conquer）：
    • 通过递归的方式，分别对第一步中产生的“小于基准的子数组”和“大于等于基准的子数组”重复进行快速排序。
  3. 合并（Combine）：
    • 这一步在快速排序中是“隐式”的，或者说不需要任何操作。因为当左右两个子数组都被排好序之后，由于分区操作已经保证了基准的正确位置以及左右两边的元素都小于或大于它，所以整个数组自然就是有序的了。

简单来说，快速排序就是通过不断地选择基准、进行分区，将一个大问题递归地分解成越来越小的子问题，直到子问题小到可以直接解决（数组只有一个或零个元素），最终完成排序。

Lumuto 分区方案

“分区”是快速排序算法的核心步骤，而 Lomuto 分区方案（Lomuto Partition Scheme）是实现分区的一种非常直观和流行的方法。

Lomuto 分区的思想

可以把它想象成整理书架的过程：

  1. 选定一本“基准书”：为了方便，可以选择书架上最右边的那本书作为基准。
  2. 划分“已整理区域”：在书架的最左边划定一个“已整理区域”，这个区域里将只放比“基准书”更薄的书。用一个标记 i 来表示这个区域的右边界。初始时，这个区域是空的，所以 i 在书架的最左端之前（i = left - 1）。
  3. 遍历检查与整理：
    • 从左到右（用一个指针 j）检查每一本书（除了最右边的基准书）。
    • 如果发现一本比“基准书”薄的书（arr[j] < pivot），需要把它放到“已整理区域”中。
    • 如何放？先把“已整理区域”的边界 i 向右移动一格（i++），然后把这本新发现的薄书 arr[j] 和边界 i 所在位置的书进行交换。这样，“已整理区域”就扩大了，并且包含了这本新发现的薄书。
  4. “基准书”归位：
    • 当检查完所有书后，[left, i] 这个区间就全都是比基准书薄的书了。
    • 那么，i+1 这个位置，理所当然就是“基准书”应该在的最终位置。
    • 最后一步，就是把“基准书”（原来在最右边 arr[right]）和 arr[i+1] 进行交换。
  5. 完成：分区操作结束，返回基准书的新位置 i+1。
参考代码

P1177 【模板】排序

#include <cstdio>
#include <vector>
#include <algorithm>
using std::vector;
using std::swap;
/**
 * @brief Lumuto 分区函数
 * @param arr   要分区的数组
 * @param left  区间的左边界索引
 * @param right 区间的右边界索引
 * @return      基准元素在分区后的最终索引
 */
int lomutoPartition(vector<int> &arr, int left, int right) {
    // 1. 选择区间的最后一个元素作为基准
    int pivot_value = arr[right];
    // i 是“小于基准”这个区域的右边界
    // 初始时，这个区域为空，i 指向 left 的前一个位置
    int i = left - 1;
    // 2. 遍历数组从 left 到 right-1
    for (int j = left; j < right; j++) {
        // 如果当前元素 arr[j] 小于基准值
        if (arr[j] < pivot_value) {
            // 扩大“小于基准”的区域
            i++;
            // 将 arr[j] 交换到这个区域的末尾
            swap(arr[i], arr[j]);
        }
    }
    // 3. 遍历结束后，i+1 的位置就是基准应该在的地方
    // 将基准（arr[right]）与 arr[i+1] 交换
    swap(arr[i + 1], arr[right]);
    // 4. 返回基准的最终位置
    return i + 1;
}
/**
 * @brief 快速排序的递归实现
 * @param arr   要排序的数组
 * @param left  区间的左边界索引
 * @param right 区间的右边界索引
 */
void quickSort(vector<int> &arr, int left, int right) {
    // 递归的终止条件：当区间只有一个或零个元素时
    if (left < right) {
        // 调用 Lomuto 分区，获取基准的最终位置
        int pivot_index = lomutoPartition(arr, left, right);
        // 递归地对基准左边的子数组进行排序
        quickSort(arr, left, pivot_index - 1);
        // 递归地对基准右边的子数组进行排序
        quickSort(arr, pivot_index + 1, right);
    }
}
int main()
{
    int n; scanf("%d", &n);
    vector<int> arr(n);
    for (int i = 0; i < n; i++) scanf("%d", &arr[i]);
    // 调用快速排序
    quickSort(arr, 0, n - 1);
    for (int i = 0; i < n; i++) {
        printf("%d%c", arr[i], i == n - 1 ? '\n' : ' ');
    }
    return 0;
}

上面这个程序并不能通过模板题的全部测试数据，这是因为标准快速排序存在弱点。

Lomuto 分区方案通常选择区间的最后一个元素作为基准（Pivot），问题就出在这个“固定”的选择上。

  • 最坏情况：如果输入的数组恰好是已经排好序的或完全逆序的。
  • 会发生什么？
    • 假设数组是 [1, 2, 3, 4, 5]，每次都选最后一个元素做基准。
    • 第一次分区，基准是 5。分区后，左边子数组是 [1, 2, 3, 4]（\(n-1\) 个元素），右边子数组是空的。
    • 第二次分区，基准是 4。分区后，左边是 [1, 2, 3]（\(n-2\) 个元素），右边是空的。
    • ...以此类推。
  • 灾难性后果：每次分区都极不均衡，递归的深度是 \(n\)，算法的时间复杂度为 \(O(n^2)\)。

随机化思想

随机快速排序（Randomized Quick Sort） 的思想非常简单，却很有效。

在选择基准时，不再固定地选择最后一个元素，而是在当前待排序的 [left, right] 区间内，随机挑选一个元素作为基准。

这样做的好处是什么？简单来说，随机化用一个可以忽略不计的“坏运气”风险，换来了在任何输入下都极其稳定的高性能。

参考代码

P1177 【模板】排序

#include <cstdio>
#include <vector>
#include <algorithm>
#include <random>
using std::vector;
using std::swap;
using std::random_device;
using std::mt19937;
using std::uniform_int_distribution;
/**
 * @brief Lumuto 分区函数
 * @param arr   要分区的数组
 * @param left  区间的左边界索引
 * @param right 区间的右边界索引
 * @return      基准元素在分区后的最终索引
 */
int lomutoPartition(vector<int> &arr, int left, int right) {
    int pivot_value = arr[right];
    int i = left - 1;
    for (int j = left; j < right; j++) {
        if (arr[j] < pivot_value) {
            i++;
            swap(arr[i], arr[j]);
        }
    }
    swap(arr[i + 1], arr[right]);
    return i + 1;
}
/**
 * @brief 快速排序的递归实现
 * @param arr   要排序的数组
 * @param left  区间的左边界索引
 * @param right 区间的右边界索引
 */
void randomizedQuickSort(vector<int> &arr, int left, int right) {
    if (left < right) {
        // 使用 <random> 库生成随机数
        // 1. 创建一个随机数生成引擎
        static mt19937 generator(random_device{}());
        // 2. 创建一个均匀分布，范围是 [left, right]
        uniform_int_distribution<int> distribution(left, right);
        // 3. 生成一个随机索引
        int pivot_idx = distribution(generator);

        // 将随机选择的基准与区间的最后一个元素交换
        swap(arr[pivot_idx], arr[right]);
        // 调用标准 Lomuto 分区
        int partition_idx = lomutoPartition(arr, left, right);
        // 4. 递归地对左右两个子数组进行排序
        randomizedQuickSort(arr, left, partition_idx - 1);
        randomizedQuickSort(arr, partition_idx + 1, right);
    }
}
int main()
{
    int n; scanf("%d", &n);
    vector<int> arr(n);
    for (int i = 0; i < n; i++) scanf("%d", &arr[i]);
    randomizedQuickSort(arr, 0, n - 1);
    for (int i = 0; i < n; i++) {
        printf("%d%c", arr[i], i == n - 1 ? '\n' : ' ');
    }
    return 0;
}

上面的程序相比之前多通过了一个测试点，但依然不能通过全部测试数据。实际上，上面的算法在重复元素多时会遇到性能瓶颈。

回顾一下 Lomuto 分区方案：if (arr[j] < pivot_value) 这个条件将数组分成了两部分：

  1. < pivot 的部分
  2. >= pivot 的部分

问题就出在这里：所有与基准值相等的元素，都被划分到了“大于等于”这一侧。

  • 设想一个极端情况：数组为 [5, 5, 5, 5, 5, 5, 5]。
  • 随机选择一个基准，必然是 5。
  • Lomuto 分区后，会得到什么？
    • 左边子数组（< 5）：空的（\(0\) 个元素）。
    • 右边子数组（>=5）：[5, 5, 5, 5, 5, 5]（\(n-1\) 个元素）。
  • 后果：这又一次导致了极不均衡的划分，时间复杂度退化为 \(O(n^2)\)。随机化在这里也无能为力，因为无论选哪个元素，基准都是 5。

荷兰国旗思想：三向切分（3-Way Partitioning）

荷兰国旗由红、白、蓝三色组成。荷兰国旗思想就是将一个数组一次性划分成三个部分，而不是两个。

应用到快速排序中，就是将数组根据基准 pivot 分成：

  1. 小于区：所有元素都比 pivot 小。
  2. 等于区：所有元素都等于 pivot。
  3. 大于区：所有元素都比 pivot 大。

这个思想的巨大优势在于：分区结束后，中间的“等于区”的所有元素已经处于其最终的排序位置了，完全不需要 在后续的递归中处理它们。只需要递归地去排序“小于区”和“大于区”即可。

如果一个数组包含大量重复元素，那么这个“等于区”会非常大，一次性就排好了很多元素，极大地减少了递归的规模。

三向切分的实现步骤

使用三个指针来完成这个精巧的操作：

  • low：指向“小于区”的 下一个位置。[left...low-1] 是小于区。
  • mid：当前正在遍历和检查的元素。[low...mid-1] 是等于区。
  • high：指向“大于区”的 前一个位置。[high+1...right] 是大于区。

遍历过程（while (mid <= high)）

  1. 如果 arr[mid] < pivot：
    • 说明 arr[mid] 属于“小于区”。
    • 将 arr[low] 和 arr[mid] 交换。
    • low 和 mid 都向右移动一位。
  2. 如果 arr[mid] == pivot：
    • 说明 arr[mid] 已经在正确的分区（等于区）了。
    • 只需要移动 mid 指针，扩大等于区即可。
  3. 如果 arr[mid] > pivot：
    • 说明 arr[mid] 属于“大于区”。
    • 将 arr[high] 和 arr[mid] 交换。
    • high 向左移动一位。
    • 注意：此时 mid 不移动。因为从 high 换过来的那个新 arr[mid] 还没有被检查过，它需要留在原地，在下一轮循环中被判断。

当 mid 指针与 high 指针相遇后，整个分区就完成了。

参考代码

P1177 【模板】排序

#include <cstdio>
#include <vector>
#include <utility>
#include <random>
using std::vector;
using std::pair;
using std::swap;
using std::mt19937;
using std::random_device;
using std::uniform_int_distribution;
/**
 * @brief 荷兰国旗问题（三向切分）分区函数
 * @param arr   要分区的数组
 * @param left  区间的左边界索引
 * @param right 区间的右边界索引
 * @return      一个 pair，包含“等于区”的左右边界索引 {low, high}
 */
pair<int, int> threeWayPartition(vector<int> &arr, int left, int right) {
    int pivot_value = arr[right];
    int low = left;     // 小于区的右边界+1
    int mid = left;     // 当前检查的元素
    int high = right;   // 大于区的左边界-1
    while (mid <= high) {
        if (arr[mid] < pivot_value) {
            swap(arr[low], arr[mid]);
            low++; mid++;
        } else if (arr[mid] > pivot_value) {
            swap(arr[high], arr[mid]);
            high--;
        } else { // arr[mid] == pivot_value
            mid++;
        }
    }
    // 循环结束后，[left, low-1] < pivot, [low, high] == pivot, [high+1, right] > pivot
    // 但由于基准在最右边，所以最后返回的等于区的边界是 [low, high]
    // 实际上，等于区的边界是 [low, mid-1]，但 high 在循环结束时就是 mid-1
    // 所以返回 {low, high} 是可以的，代表等于区的开始和结束
    return {low, high};
}
/**
 * @brief 随机快速排序函数（三向切分优化版）
 * @param arr   要排序的数组
 * @param left  区间的左边界索引
 * @param right 区间的右边界索引
 */
void randomizedQuickSort(vector<int> &arr, int left, int right) {
    if (left >= right) return;
    // 随机化：选择一个随机基准并与最后一个元素交换
    static mt19937 generator(random_device{}());
    uniform_int_distribution<int> distribution(left, right);
    int pivot_idx = distribution(generator);
    swap(arr[pivot_idx], arr[right]);
    // 执行三向切分
    pair<int, int> partition_indices = threeWayPartition(arr, left, right);
    // 递归地对“小于区”和“大于区”进行排序
    // “等于区” [partition_indices.first, partition_indices.second] 不再需要处理
    randomizedQuickSort(arr, left, partition_indices.first - 1);
    randomizedQuickSort(arr, partition_indices.second + 1, right);
}
int main()
{
    int n; scanf("%d", &n);
    vector<int> arr(n);
    for (int i = 0; i < n; i++) scanf("%d", &arr[i]);
    randomizedQuickSort(arr, 0, n - 1);
    for (int i = 0; i < n; i++) {
        printf("%d%c", arr[i], i == n - 1 ? '\n' : ' ');
    }
    return 0;
}

Hoare 分区方案

Hoare 分区方案由快速排序算法的发明者 C. A. R. Hoare 本人提出，是最初的分区方法。它的思想与 Lomuto 方案有所不同，更为精巧。

核心思想：使用两个指针，一个从 左端开始向右 扫描，另一个从 右端开始向左 扫描，它们相向而行，寻找并交换那些“站错队”的元素。

  1. 选择基准（Pivot）：
    • Hoare 方案通常选择 区间的第一个元素 arr[left] 作为基准。
    • 注意：这个基准在整个分区过程中不会移动，它只是一个用于比较的“标杆”。
  2. 初始化指针：
    • 左指针 i 初始化为 left - 1。
    • 右指针 j 初始化为 right + 1。
    • 这种“界外”初始化是为了方便在 do-while 循环中先移动再访问。
  3. 相向扫描与交换：
    • 进入一个无限循环 while (true)。
    • 左指针 i 的移动：i 不断向右移动（i++），直到找到一个 大于或等于 基准 pivot 的元素 arr[i] 才停下。
    • 右指针 j 的移动：j 不断向左移动（j--），直到找到一个 小于或等于 基准 pivot 的元素 arr[j] 才停下。
    • 判断与操作：
      • 如果此时 i >= j，说明两个指针已经相遇或交错，这意味着整个区间已经被扫描完毕，分区过程结束。返回 j 作为分割点。
      • 如果 i < j，说明 i 和 j 各自找到了一个“站错队”的元素（arr[i] 在左边但偏大，arr[j] 在右边但偏小），此时 交换 arr[i] 和 arr[j]。交换后，继续下一轮的扫描。

Hoare 方案的一个关键特性

与 Lomuto 方案不同，Hoare 分区结束后：

  • 它不保证基准元素最终位于 j 这个位置上。
  • 它只保证 [left, j] 区间内的所有元素都 小于或等于 基准。
  • 它只保证 [j+1, right] 区间内的所有元素都 大于或等于 基准。

这对递归调用意味着什么？

  • 因为分割点 j 可能不是基准的最终位置，所以递归处理的子数组必须是 [left, j] 和 [j+1, right]。
  • 不能像 Lomuto 方案那样将分割点排除在外（即 [left, j-1]），否则如果 j 恰好是基准所在的位置，可能会导致无限递归。
参考代码

P1177 【模板】排序

#include <cstdio>
#include <vector>
#include <utility>
#include <random>
using std::vector;
using std::swap;
using std::mt19937;
using std::uniform_int_distribution;
using std::random_device;
/**
 * @brief Hoare 分区函数
 * @param arr   要分区的数组
 * @param left  区间的左边界索引
 * @param right 区间的右边界索引
 * @return      一个分割点索引 j，使得 [left, j] <= pivot 且 [j+1, right] >= pivot
 */
int hoarePartition(vector<int> &arr, int left, int right) {
    // 1. 选择第一个元素作为基准
    int pivot_value = arr[left];

    int i = left - 1, j = right + 1;

    while (true) {
        // 2. 从左向右找到第一个 >= pivot 的元素
        do {
            i++;
        } while (arr[i] < pivot_value);
        // 3. 从右向左找到第一个 <= pivot 的元素
        do {
            j--;
        } while (arr[j] > pivot_value);
        // 4. 如果指针相遇或交错，分区完成
        if (i >= j) return j;
        // 5. 交换站错队的元素
        swap(arr[i], arr[j]); 
    }
}
/**
 * @brief 随机快速排序函数（Hoare 分区版）
 * @param arr   要排序的数组
 * @param left  区间的左边界索引
 * @param right 区间的右边界索引
 */
void randomizedQuickSort(vector<int> &arr, int left, int right) {
    if (left < right) {
        // 随机化：选择一个随机基准并与第一个元素交换
        static mt19937 generator(random_device{}());
        uniform_int_distribution<int> distribution(left, right);
        int pivot_idx = distribution(generator);
        swap(arr[pivot_idx], arr[left]);
        // 执行 Hoare 分区
        int partition_idx = hoarePartition(arr, left, right);
        // 递归地对左右两个子数组进行排序
        // 注意这里的递归边界
        randomizedQuickSort(arr, left, partition_idx);
        randomizedQuickSort(arr, partition_idx + 1, right);
    }
}
int main()
{
    int n; scanf("%d", &n);
    vector<int> arr(n);
    for (int i = 0; i < n; i++) scanf("%d", &arr[i]);
    randomizedQuickSort(arr, 0, n - 1);
    for (int i = 0; i < n; i++) {
        printf("%d%c", arr[i], i == n - 1 ? '\n' : ' ');
    }
    return 0;
}

时间复杂度分析

快速排序的时间复杂度取决于 分区（Partition） 操作的好坏，而分区的好坏又取决于 基准（Pivot） 的选择。

  • 最佳情况（Best Case）：每次选择的基准都恰好是当前子数组的 中位数。这会将数组完美地划分为两个大小几乎相等的子数组。
  • 最坏情况（Worst Case）：每次选择的基准都恰好是当前子数组的 最小值 或 最大值。这会导致分区极不均衡，一边是 \(n-1\) 个元素，另一边是 \(0\) 个元素。

最佳情况分析

如果每次都能完美地平分数组，那么处理一个大小为 \(n\) 的问题，需要：

  • 对大小为 \(n/2\) 的左子数组进行排序。
  • 对大小为 \(n/2\) 的右子数组进行排序。
  • 分区操作本身需要遍历整个数组，成本为 \(O(n)\)。
  • 因此，递归关系式为：\(T(n) = 2 T(n/2) + O(n) = O(n \log n)\)。

最坏情况分析

对于 随机 快速排序，最坏情况是指 运气差到极点，每次随机选择都恰好选中了当前子数组的最大或最小值。

如果每次分区都产生一个 \(n-1\) 和一个 \(0\) 的划分，递归关系式为：\(T(n)=T(n-1)+O(n)=O(n^2)\)。

最坏情况 \(O(n^2)\) 听起来很吓人，但 随机化 使得这种情况在实践中几乎不可能发生。数学家证明这种算法的平均时间复杂度是 \(O(n \log n)\)。

当算法的最坏时间复杂度的发生概率较小时，平均意义下的时间耗用能够更加准确地度量算法的性能。算法在所有实例上的平均时间耗用，称为算法的平均时间复杂度。

选择题：假设快速排序算法的输入是一个长度为 \(n\) 的已排序数组，且该快速排序算法在分治过程总是选择第一个元素作为基准元素。以下哪个选项描述的是在这种情况下的快速排序行为？

  • A. 快速排序对于此类输入的表现最好，因为数组已经排序。
  • B. 快速排序对于此类输入的时间复杂度是 \(O(n \log n)\)。
  • C. 快速排序对于此类输入的时间复杂度是 \(O(n^2)\)。
  • D. 快速排序无法对此类数组进行排序，因为数组已经排序。
答案

C

选择题：考虑对 n 个数进行排序，以下最坏时间复杂度低于 \(O(n^2)\) 的排序方法是？

  • A. 插入排序
  • B. 冒泡排序
  • C. 归并排序
  • D. 快速排序
答案

正确答案是 C。

  • 插入排序：最坏情况（例如，待排序数组是逆序的）下，每个元素都需要和前面所有已排序的元素进行比较和移动，时间复杂度为 \(O(n^2)\)。
  • 冒泡排序：最坏情况（例如，待排序数组是逆序的）下，需要进行 \(n-1\) 轮比较和交换，总的时间复杂度为 \(O(n^2)\)。
  • 归并排序：归并排序是一种分治算法，无论输入数组的初始顺序如何，它都稳定地将数组分成两半，然后合并，其分解和合并的过程所花费的时间都与 \(O(n \log n)\) 成正比。因此，它的最坏时间复杂度为 \(O(n \log n)\)。
  • 快速排序：快速排序的平均时间复杂度是 \(O(n \log n)\)，但其最坏情况（例如，每次选取的基准值都是当前数组的最小值或最大值）会导致算法退化，时间复杂度变为 \(O(n^2)\)。

综上所述，只有归并排序的最坏时间复杂度 \(O(n \log n)\) 低于 \(O(n^2)\)。

选择题：排序的算法很多，若按排序的稳定性和不稳定性分类，则下列哪个是不稳定排序？

  • A. 冒泡排序
  • B. 直接插入排序
  • C. 快速排序
  • D. 归并排序
答案

C。

程序阅读题

#include <iostream>
using namespace std;

const int N = 1000;
int c[N];

int logic(int x, int y) {
    return (x & y) ^ ((x ^ y) | (~x & y));
}

void generate(int a, int b, int *c) {
    for (int i = 0; i < b; i++)
        c[i] = logic(a, i) % (b + 1);
}

void recursion(int depth, int *arr, int size) {
    if (depth <= 0 || size <= 1) return;
    int pivot = arr[0];
    int i = 0, j = size - 1;
    while (i <= j) {
        while (arr[i] < pivot) i++;
        while (arr[j] > pivot) j--;
        if (i <= j) {
            int temp = arr[i];
            arr[i] = arr[j];
            arr[j] = temp;
            i++; j--;
        }
    }
    recursion(depth - 1, arr, j + 1);
    recursion(depth - 1, arr + i, size - i);
}

int main() {
    int a, b, d;
    cin >> a >> b >> d;
    generate(a, b, c);
    recursion(d, c, b);
    for (int i = 0; i < b; ++i) cout << c[i] << " ";
    cout << endl;
}

判断题

  1. 当 \(1000 \ge d \ge b\) 时，输出的序列是有序的。

  2. 当输入 5 5 1 时，输出为 1 1 5 5 5。

  3. 假设数组 \(c\) 长度无限制，该程序所实现的算法的时间复杂度是 \(O(b)\) 的。

选择题

  1. 函数 int logic(int x, int y) 的功能是？
  • A. 按位与
  • B. 按位或
  • C. 按位异或
  • D. 以上都不是
  1. 当输入为 10 100 100 时，输出的第 100 个数是？
  • A. 91
  • B. 94
  • C. 95
  • D. 98
答案

代码分析

  1. logic(int x, int y) 函数：这个函数执行了一系列位运算，乍一看是一个比较复杂的式子。但是考虑到位运算是独立的，因此把 \(x,y\) 的每一位等于 0 或 1 的情况代入计算就可发现，只有都等于 0 时结果才为 0，否则结果为 1，而这实际上就相当于是按位或。
  2. generate(int a, int b, int c) 函数：这个函数会用 logic 函数的结果来填充数组 c，它会计算 c[i] = (a | i) % (b + 1)，其中 i 从 0 到 b-1。
  3. recursion(int depth, int *arr, int size) 函数：这是一个实现了快速排序的递归函数。
    • 它使用数组的第一个元素作为基准值 pivot。
    • depth 参数限制了递归的深度，如果 depth 耗尽，递归就会停止。
    • 如果 depth 的值足够大（例如，大于等于数组大小 b），这个函数就能将数组完全排序。如果 depth 很小，相当于快速排序只进行了几趟。

判断题

  1. 正确。recursion 函数是一个快速排序实现，在最坏的情况下（例如，数组已经有序或逆序），快速排序需要的递归深度等于数组的长度 b。题目条件 d \ge b 保证了递归深度 d 总是足够完成排序，不会因为深度限制而提前终止。

  2. 错误。根据前面对 generate 函数的理解可以发现，c[0] = (5|0)%6 = 5; c[1] = (5|1)%6 = 5; c[2] = (5|2)%6 = 7%6 = 1; c[3] = (5|3)%6 = 7%6 = 1; c[4] = (5|4)%6 = 5;，初始数组 c 为 {5, 5, 1, 1, 5}。depth 为 1，表示只执行一层分区操作。pivot = c[0] = 5，分区过程会不停交换左侧的一个大于等于基准值的元素和右侧的一个小于等于基准值的元素，最终结果为 {5, 1, 1, 5, 5}。

  3. 错误。程序总的时间复杂度由 generate 和 recursion 决定，generate 的复杂度是 \(O(b)\)，recursion 的复杂度是 \(O(d \times b)\)，因为它执行 \(d\) 层的分区，每层分区操作的总时间是 \(O(b)\)。总复杂度为 \(O(b)+O(d \times b) = O(d \times b)\)，因为 \(d\) 是一个输入变量，不能被当作常数，所以时间复杂度依赖于 \(d\) 和 \(b\)。

选择题

  1. B。如上面的代码分析所示，功能为按位或。

  2. C。输入满足 d >= b 的条件，所以 recursion 函数会将数组 c 完全排序。问题所求的“第 100 个数”就是排序后数组的最后一个元素，也就是数组中的最大值。需要找到 c[i] = (10 | i) % 101 在 i 从 0 到 99 的范围内的最大值。分析 (10 | i) 的可能值，i 的最大值是 99，所以 10 | i 的值不会超过 107。需要找到 i 使得 (10 | i) 在模 101 之后最大。情况一：10 | i >= 101，10 | 99 = 107, 107 % 101 = 6，10 | 98 = 106, 106 % 101 = 5，其他 10 | i 的值都小于 106，所以这种情况下，能产生的最大余数是 6。情况二：10 | i < 101，在这种情况下，(10 | i) % 101 就等于 10 | i。需要找到 i 使得 10 | i 的值最大，且小于 101。此时相当于优先满足最高位，权值为 \(2^6 = 64\) 的位可以为 1，这样按位或上 10 之后是 74，接下来考虑权值位 $2^5 = 32 $ 的位，这一位不能得到 1，不然结果就超过 101 了，以此类推，最终能得到的最大结果是 \(2^6 + 2^4 + 2^3 + 2^2 + 2^1 + 2^0 = 95\)。因此，数组 c 中的最大值是 95，排序后，第 100 个数就是 95。

快速选择

快速选择算法用于高效地从一个无序数组中找到第 k 大或第 k 小的元素。

一个直接的想法是先对整个数组进行排序，如何直接返回对应索引的元素。这样做时间复杂度是 \(O(n \log n)\)，属于杀鸡用牛刀，为了仅仅找到一个元素，把整个数组都排好序了，做了很多不必要的工作。

快速选择算法的优势在于：它能在平均 \(O(n)\) 的线性时间内找到这个元素，这在理论上是能达到的最优平均时间复杂度。它避免了对整个数组进行排序，只关注包含目标元素的那一部分数据，从而大大减少了计算量。

它的核心思想巧妙地借鉴了快速排序。

  1. 核心操作——分区：快速排序的第一步是“分区”。
    • 从数组中选一个元素作为基准。
    • 重新排列数组，使得所有小于基准的元素都在它左边，所有大于基准的元素都在它右边。
    • 完成这一步后，这个基准就已经被放到了它最终排好序后应该在的位置。
  2. 快速选择的选择性递归：以三向分区为例，在分区操作完成后，假设基准在排序后的最终位置应该是 \([l,r]\)：
    • 如果要找的最终索引 k 正好在这个区间，那说明这个基准就是对应的元素值。
    • 如果 k < l，说明要找的元素肯定在基准的左边。完全不需要关心右边的子数组了，只需要在左边的子数组中继续寻找。
    • 如果 k > r，说明要找的元素肯定在基准的右边。同样舍弃左边的部分，只需要在右边的子数组中继续寻找。

与快速排序的关键区别：

  • 快速排序需要递归处理左右两个子数组。
  • 快速选择只递归处理其中一个子数组，问题规模迅速减小。

这种“只走一边”的策略，就是它能达到 \(O(n)\) 平均时间复杂度的根本原因。

参考代码

P1923 【深基9.例4】求第 k 小的数

#include <cstdio>
#include <vector>
#include <utility>
#include <random>
using namespace std;
pair<int, int> threeWayPartition(vector<int> &arr, int left, int right) {
    int pivot_value = arr[right];
    int low = left;     // 小于区的右边界+1
    int mid = left;     // 当前检查的元素
    int high = right;   // 大于区的左边界-1
    while (mid <= high) {
        if (arr[mid] < pivot_value) {
            swap(arr[low], arr[mid]);
            low++; mid++;
        } else if (arr[mid] > pivot_value) {
            swap(arr[high], arr[mid]);
            high--;
        } else { // arr[mid] == pivot_value
            mid++;
        }
    }
    return {low, high};
}
int quickSelect(vector<int> &nums, int left, int right, int target_idx) {
    while (left <= right) {
        static mt19937 generator(random_device{}());
        uniform_int_distribution<int> distribution(left, right);
        int pivot_idx = distribution(generator);
        swap(nums[pivot_idx], nums[right]);

        // 执行三向划分，返回等于基准值区域的左右边界 [lt, gt]
        pair<int, int> pivot_range = threeWayPartition(nums, left, right);
        int lt = pivot_range.first, gt = pivot_range.second;
        if (target_idx >= lt && target_idx <= gt) {
            // 目标索引落在等于区域，找到了答案
            return nums[lt];
        } else if (target_idx < lt) {
            // 目标在小于区域，更新右边界，继续在左边查找
            right = lt - 1;
        } else { // target_idx > gt
            // 目标在大于区域，更新左边界，继续在右边查找
            left = gt + 1;
        }
    }
    // 理论上在有效输入下不会到达这里
    return -1;
}
int main()
{
    int n, k; scanf("%d%d", &n, &k);
    vector<int> a(n);
    for (int i = 0; i < n; i++) scanf("%d", &a[i]);
    printf("%d\n", quickSelect(a, 0, n - 1, k));
    return 0;
}

例题：P1115 最大子段和

要找到整个序列的最大子段和，可以将其一分为二，从中点 \(mid\) 分成左右两个子序列：\(a_{left \dots mid}\) 和 \(a_{mid+1 \dots right}\)。

此时，最大子段和可能存在于三个位置：

  • 完全在左半部分：即 \(a_{left \dots mid}\) 内部。
  • 完全在右半部分：即 \(a_{mid+1 \dots right}\) 内部。
  • 跨越中点：这个子段既包含了左半部分的元素，也包含了右半部分的元素，并且一定跨过 \(mid\) 和 \(mid+1\)。

对于前两种情况，可以递归地求解来得到答案。递归的终止条件是当子序列只有一个元素时，最大子段和就是该元素自身的值。

对于第三种情况，即跨越中点的情况，无法直接通过递归得到。此时需要专门解决：

  • 从 \(mid\) 开始向左遍历，找到一个以 \(mid\) 结尾的最大子段和。
  • 从 \(mid+1\) 开始向右遍历，找到一个以 \(mid+1\) 开头的最大子段和。
  • 将这两个和相加，就得到了跨越中点的最大子段和。

比较上述三种情况得出的三个值，取其中最大者，即为当前问题的最终解。

这个分治算法的递推关系式是 \(T(n) = 2T(n/2) + O(n) = O(n \log n)\)。

参考代码 
#include <cstdio>
#include <algorithm> 

using namespace std;

const int N = 2e5 + 5;

int a[N];

/**
 * @brief 计算跨越中点的最大子段和
 * @param left 区间左边界
 * @param mid 区间中点
 * @param right 区间右边界
 * @return 返回跨越中点的最大子段和
 * @note 这个函数的线性扫描是整个分治算法时间复杂度为 O(n log n) 的原因
 */
int maxCrossingSum(int left, int mid, int right) {
    int sum = 0;
    // 初始化左半部分的最大和为一个极小值，这里直接用 a[mid] 作为初始值
    int left_sum = a[mid]; 
    
    // 从中点 `mid` 开始向左遍历，寻找以 a[mid] 结尾的最大连续和
    for (int i = mid; i >= left; i--) {
        sum += a[i];
        if (sum > left_sum) {
            left_sum = sum;
        }
    }

    // 重置 sum，准备计算右半部分
    sum = 0;
    // 初始化右半部分的最大和
    int right_sum = a[mid + 1];

    // 从 `mid + 1` 开始向右遍历，寻找以 a[mid+1] 开头的最大连续和
    for (int i = mid + 1; i <= right; i++) {
        sum += a[i];
        if (sum > right_sum) {
            right_sum = sum;
        }
    }
    
    // 跨越中点的最大子段和等于左、右两部分最大和之和
    return left_sum + right_sum;
}

/**
 * @brief 使用分治法递归求解最大子段和
 * @param left 区间左边界
 * @param right 区间右边界
 * @return 返回 a[left...right] 区间的最大子段和
 */
int maxSubArraySum(int left, int right) {
    // 递归的终止条件：如果区间只有一个元素，最大子段和就是它本身
    if (left == right) {
        return a[left];
    }

    // --- 1. 分解 (Divide) ---
    int mid = left + (right - left) / 2;

    // --- 2. 解决 (Conquer) ---
    // 递归求解左半部分的最大子段和
    int left_max = maxSubArraySum(left, mid);
    // 递归求解右半部分的最大子段和
    int right_max = maxSubArraySum(mid + 1, right);
    // 求解跨越中点的最大子段和
    int cross_max = maxCrossingSum(left, mid, right);

    // --- 3. 合并 (Combine) ---
    // 返回三种情况中的最大值
    return std::max({left_max, right_max, cross_max});
}

int main() {
    int n;
    scanf("%d", &n);

    for (int i = 1; i <= n; i++) {
        scanf("%d", &a[i]);
    }

    printf("%d\n", maxSubArraySum(1, n));
    
    return 0;
}

这个算法可以进一步改进，使其时间复杂度达到 \(O(n)\)。算法思想仍然是“分治”，但通过在“合并”步骤中进行优化，避免了 \(O(n \log n)\) 解法中重复的线性扫描，从而达到了 \(O(n)\) 的效率。

之前的分治法在“合并”步骤需要 \(O(n)\) 时间来计算跨越中点的最大和，为了优化这一点，必须让“合并”操作在 \(O(1)\) 时间内完成。

如何做到呢？诀窍在于递归函数返回更多的信息，而不仅仅是“最大子段和”。

对于任意一个区间 \(a_{left \dots right}\)，维护以下四个值：

  1. max_sum：该区间的最大子段和（这是最终的答案）。
  2. prefix_sum：包含该区间最左侧元素 \(a_{left}\) 的最大子段和。
  3. suffix_sum：包含该区间最右侧元素 \(a_{right}\) 的最大子段和。
  4. total_sum：该区间所有元素的总和。

将这四个值封装在一个结构体里。

和之前一样，将区间 \(a_{left \dots right}\) 分为 \(a_{left \dots mid}\) 和 \(a_{mid+1 \dots right}\)。递归地调用函数，获取左右两个子区间的信息包（称之为 l 和 r）。

现在，利用 l 和 r 在 \(O(1)\) 的时间内计算出整个区间 \(a_{left \dots right}\) 的信息包 res。

  • 显然，整体的总和是左右两边的总和相加。res.total_sum = l.total_sum + r.total_sum。
  • 整个区间的“最大前缀和”有两种可能，左半部分的“最大前缀和”，或者它跨越了中点，等于左半部分的“总和”加上右半部分的“最大前缀和”。取这两者的较大值：res.prefix_sum = max(l.prefix_sum, l.total_sum + r.prefix_sum)。
  • 与前缀和对称，整个区间的“最大后缀和”也有两种可能，右半部分的“最大后缀和”，或者它跨越了中点，等于右半部分的“总和”加上左半部分的“最大后缀和”。取这两者的较大值：res.suffix_sum = max(r.suffix_sum, r.total_sum + l.suffix_sum)。
  • 整个区间的“最大子段和”有三种可能：左半部分的“最大子段和”，右半部分的“最大子段和”，或者它跨越了中点，这个跨越中点的最大和，恰好等于左半部分的“最大后缀和”与右半部分的“最大前缀和”之和。取这三者的最大值：res.max_sum = max({l.max_sum, r.max_sum, l.suffix_sum + r.prefix_sum})。

通过这种方式，每次合并都只需要几次简单的加法和比较，是 \(O(1)\) 操作。

递推关系式变为 \(T(n) = 2T(n/2) + O(1) = O(n)\)。

参考代码 
#include <cstdio>
#include <algorithm> 

using namespace std;

const int N = 2e5 + 5;

int a[N];

// 定义一个结构体来存储区间信息 
struct SubArrayInfo {
    int max_sum;    // 区间最大子段和
    int prefix_sum; // 包含左边界的最大子段和   
    int suffix_sum; // 包含右边界的最大子段和
    int total_sum;  // 区间总和 
};

// 合并两个子区间信息的函数
SubArrayInfo pushUp(const SubArrayInfo& l, const SubArrayInfo& r) {
    SubArrayInfo res;
    // 计算总和
    res.total_sum = l.total_sum + r.total_sum;
    // 计算最大前缀和
    res.prefix_sum = max(l.prefix_sum, l.total_sum + r.prefix_sum);
    // 计算最大后缀和   
    res.suffix_sum = max(r.suffix_sum, r.total_sum + l.suffix_sum);
    // 计算最大子段和
    int cross_max = l.suffix_sum + r.prefix_sum;
    res.max_sum = max({l.max_sum, r.max_sum, cross_max});
    return res;  
}

// O(n) 分治法求解主函数
SubArrayInfo solve(int left, int right) {
    // 基本情况：区间只有一个元素
    if (left == right) { 
        int val = a[left];      
        return {val, val, val, val};
    }
    // 1. 分解     
    int mid = left + (right - left) / 2;   
    // 2. 解决
    SubArrayInfo left_info = solve(left, mid); 
    SubArrayInfo right_info = solve(mid + 1, right);
    // 3. 合并
    return pushUp(left_info, right_info); 
}

int main() {
    int n;
    scanf("%d", &n);

    for (int i = 1; i <= n; i++) {
        scanf("%d", &a[i]);
    }

    printf("%d\n", solve(1, n).max_sum);
    
    return 0;
}

阅读程序题

#include <algorithm>
#include <iostream>
using namespace std;

int n, a[1005];

struct Node 
{
	int h, j, m, w;

	Node(const int _h, const int _j, const int _m, const int _w) : 
		h(_h), j(_j), m(_m), w(_w)
	{ }

	Node operator+(const Node &o) const 
	{
		return Node(
			max(h, w + o.h),
			max(max(j, o.j), m + o.h),
			max(m + o.w, o.m),
			w + o.w);
	}
};

Node solve1(int h, int m)
{
	if (h > m)
		return Node(-1, -1, -1, -1);
	if (h == m)
		return Node(max(a[h], 0), max(a[h], 0), max(a[h], 0), a[h]);
	int j = (h + m) >> 1;
	return solve1(h, j) + solve1(j + 1, m);
}

Node solve2(int h, int m) 
{
	if (h > m)
		return -1;
	if (h == m)
		return max(a[h], 0);
	int j = (h + m) >> 1;
	int wh = 0, wm = 0;
	int wht = 0, wmt = 0;
	for (int i = j; i >= h; i--) {
		wht += a[i];
		wh = max(wh, wht);
	}
	for (int i = j + 1; i <= m; i++) {
		wmt += a[i];
		wm = max(wm, wmt);
	}
	return max(max(solve2(h, j), solve2(j + 1, m)), wh + wm);
}

int main()
{
	cin >> n;
	for (int i = 1; i <= n; i++) cin >> a[i];
	cout << solve1(1, n).j << endl;
	cout << solve2(1, n) << endl;
	return 0;
}

假设输入的所有数的绝对值都不超过 1000，完成下面的判断题和单选题：

判断题

  1. 程序总是会正常执行并输出两行两个相等的数。

  2. 第 28 行与第 38 行分别有可能执行两次及以上。

  3. 当输入为 5 -10 11 -9 5 -7 时，输出的第二行为 7。

单选题

  1. solve1(1, n) 的时间复杂度为？
  • A. \(O(\log n)\)
  • B. \(O(n)\)
  • C. \(O(n \log n)\)
  • D. \(O(n^2)\)
  1. solve2(1, n) 的时间复杂度为？
  • A. \(O(\log n)\)
  • B. \(O(n)\)
  • C. \(O(n \log n)\)
  • D. \(O(n^2)\)
  1. 当输入为 10 -3 2 10 0 -8 9 -4 -5 9 4 时，输出的第一行为？
  • A. 13
  • B. 17
  • C. 24
  • D. 12
答案

代码分析

这段代码实现了两种分治算法（solve1 和 solve2）来求解同一个问题：最大子段和。

判断题

  1. 正确。

  2. 错误。当输入的 \(n\) 小于等于 0 时，第 28 行和第 38 行会被执行到，但最多执行一次。当 \(n\) 大于 0 时，这两行不会被执行到。

  3. 错误。该数据下最大子段和应该是 11。

单选题

  1. B。

  2. C。

  3. B。\(2+10+0+(-8)+9+(-4)+(-5)+9+4=17\)。

posted @ 2023-08-07 06:10  RonChen  阅读(194)  评论(0)    收藏  举报