贪心基础
最优化问题是指，在给定的限制条件下，寻找一个方案，使得目标结果尽可能最优。例如，要从学校到北京天安门，有很多种不同的交通方案，如何选择一个最省钱的方案？
很多最优化问题，都可以看成多步决策问题，即把解决问题的过程分成若干步，每一步有若干种决策方案。在每一步做出一个决策，最终解决整个问题。
比如，以从学校到天安门的问题为例，假设分成 3 个阶段：
- 从学校到杭州东站，
- 从杭州东站到北京南站。
- 从北京南站到天安门广场。
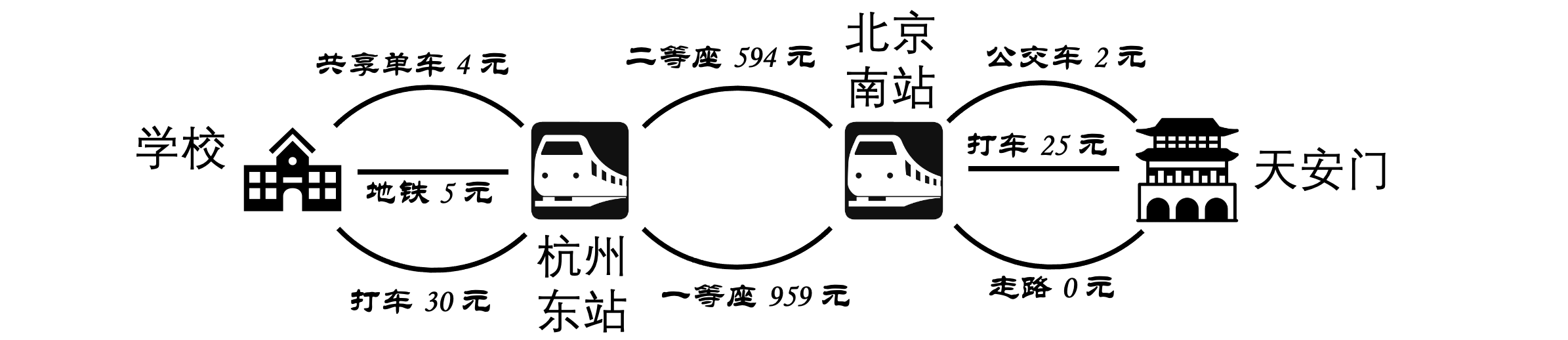
第一个阶段，从学校到杭州东站，有 3 种不同方案，分别是：骑共享单车，花费 1.5 元；乘坐地铁，花费 5 元；打车，花费 30 元。
第二个阶段，从杭州东站到北京南站，有 2 种不同方案，分别是：二等座，花费 594 元；一等座，花费 959 元。
第三个阶段，从北京南站到天安门，有 3 种不同方案，分别是：坐公交车，花费 2 元；打车，花费 25 元；走路，花费 0 元。
对于这一多步决策问题，我们采取贪心策略，既然想要总的花费最小，那么每一步决策都采取最便宜的方案，最后得到的结果也就是全局的最优解了。所以我们选择骑共享单车去杭州东站，坐二等座去北京南站，走路去天安门，总的花费是 \(4 + 594 + 0 = 598\) 元。
事实上，贪心策略不一定永远是最优的。比如在这个例子中，如果我们因为第一步选择骑车，可能导致体力不够最后的走路，只能坐公交车去天安门。这样总的花费会变成 \(4 + 594 + 2 = 600\) 元，反而不如第一步坐地铁划算。
贪心算法不是对所有问题都能得到整体最优解，关键是贪心策略的选择，选择的贪心策略必须具备无后效性，即某个状态以前的过程不会影响以后的状态，只与当前状态有关。只有贪心策略是正确的，才能使用贪心算法正确地解决该问题。在很多情况下，贪心的合理性并不是显然的，但如果能找到一个反例，就可以证明这样的贪心不正确。
从另一个角度而言，信息学竞赛不同于数学竞赛，信息学竞赛更关注最终实现的程序。所以，有时候可以采取猜结论的策略（当然最好是能证明正确性，贪心策略的证明分析可以借助一些专门的方法），考场上如果无法证明正确性，但直觉认为是对的，又无法构造反例，不妨先大胆实现。不过训练中还是应该尽量搞清楚每一个贪心问题的策略证明。
例题：P3742 umi的函数
Special Judge是指当一道题有多组解时，评测系统用一个验证程序来验证解的正确性。标有 Special Judge 的题目说明你的输出方案不一定要和样例中给出的一模一样，只需符合题目要求即可。
考虑每一个字符，我们构造的字符串 z 中的这个字符与 x 字符串中的对应字符取最小值后要对应 y 字符串中的对应字符。首先，如果结果 y 里的字符比 x 里的对应字符还要大了，那这就说明无解。而如果有解，我们可以分类讨论：如果最后结果 y 里的那个字符跟 x 里的一样，说明我们构造的 z 里这个位置上的字符不比 x 里的要小；如果最后 y 里的那个字符跟 x 里的不一样，说明是通过我们构造的 z 让结果变成 y 里的样子的，那就说明我们构造的字符就是 y 里的对应字符。综上，我们发现，如果要构造方案，最方便的就是直接令整个 z=y，因为这样既满足第一种情况（不比 x 里的对应字符更小），又满足第二种情况（就是 y 里的字符）。
#include <cstdio>
char x[105], y[105];
int main()
{
int n;
scanf("%d%s%s", &n, x, y);
bool ok = true;
for (int i = 0; i < n; i++) {
if (x[i] < y[i]) {
ok = false;
break;
}
}
if (ok) printf("%s\n", y);
else printf("-1\n");
return 0;
}
习题：CF2118A Equal Subsequences
解题思路
要让两者数量相等，最简单的方法就是让它们都等于 0。
直接把所有的 1 和所有的 0 放在两端则两种子序列数量都会是 0，这就是一种非常简单的构造方法。
参考代码
#include <cstdio>
using namespace std;
void solve() {
int n, k;
scanf("%d%d", &n, &k);
for (int i = 1; i <= k; i++) printf("1");
for (int i = 1; i <= n - k; i++) printf("0");
printf("\n");
}
int main()
{
int t;
scanf("%d", &t);
for (int i = 1; i <= t; i++) {
solve();
}
return 0;
}
习题：P11199 [JOIG 2024] ダンス / Dance
解题思路
首先，解决这类配对问题的有效策略是先对所有学生的身高进行排序。设排序后的身高为 \(a_1, a_2, \dots, a_{2N}\)，这使得身高相近的学生被排在了一起，便于考虑配对。
观察排序后的身高数组，如果相邻的两个学生 \(a_i\) 和 \(a_{i+1}\) 的身高差 \(a_{i+1} - a_i\) 大于 \(D\)，那么这意味着 \(a_i\) 和 \(a_{i+1}\) 绝对不能配对。不仅如此，任何身高小于等于 \(a_i\) 的学生（即 \(a_1, \dots, a_i\)）都不可能与任何身高大于等于 \(a_{i+1}\) 的学生（即 \(a_{i+1}, \dots, a_{2N}\)）配对，因为他们的身高差只会更大。
这些身高差大于 \(D\) 的巨大鸿沟实际上将所有学生分成了几个独立的组，例如，如果 \(a_i - a_{i-1} \gt D\)，那么 \(a_1, \dots, a_{i-1}\) 形成了一个独立的群体，他们内部的成员必须在内部配对消化，不能和外面的成员配对。
既然每个这样的独立小组都必须在内部完成配对，那么一个显而易见的必要条件是：每个小组的人数都必须是偶数。如果任何一个小组的人数是奇数，那么必然会有一个人剩下，无法完成配对。
这个条件也是充分的，如果一个小组内所有学生的人数是偶数，并且组内任意相邻学生的身高差都不超过 \(D\)，就总能找到一种配对方案。例如，最简单的方案就是将排序后的学生两两配对：\((a_1, a_2), (a_3, a_4), \dots\)。因为 \(a_2 - a_1 \le D, \ a_4 - a_3 \le D\) 等，所以这种配对是有效的。
参考代码
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 205;
int a[N];
int main()
{
int n, d; scanf("%d%d", &n, &d);
n *= 2;
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]);
}
sort(a + 1, a + n + 1);
int cnt = 1;
for (int i = 2; i <= n; i++) {
if (a[i] - a[i - 1] > d) {
if (cnt % 2 != 0) {
printf("No\n"); return 0;
}
cnt = 1;
} else {
cnt++;
}
}
if (cnt % 2 == 0) {
printf("Yes\n");
} else {
printf("No\n");
}
return 0;
}
例题：P2676 [USACO07DEC] Bookshelf B
分析：根据题目描述可以将题意理解为，尽可能使奶牛数量最少，还可以达到书架的高度 B。我们需要先将奶牛的高度从大到小进行排序，让高个子奶牛尽可能先上场，这样贪心地选择奶牛，可以使最后奶牛数量尽可能少。
排序完成之后，从身高最高的奶牛开始，累加当前所有参与“奶牛塔”的奶牛身高。如果达到了暑假高度 B，直接输出此时的奶牛数量，并跳出循环；相反，如果身高总和小于暑假高度 B，则要继续使用下一头奶牛，……，反复累加，反复判断。
#include <cstdio>
#include <algorithm>
using std::sort;
const int N = 20005;
int h[N];
int main()
{
int n, b; scanf("%d%d", &n, &b); // 输入奶牛数量和书架高度
for (int i = 1; i <= n; i++) scanf("%d", &h[i]); // 依次输入每只奶牛的身高
sort(h + 1, h + n + 1, [](int x, int y) {
return x > y; // 按从大到小排序奶牛的身高
});
int ans = 0, sum = 0;
for (int i = 1; i <= n; i++) {
sum += h[i]; ans++; // 累加每一只奶牛的身高和奶牛的数量
if (sum >= b) { // 如果达到了书架高度
printf("%d\n", ans); // 输出此时的奶牛数量
break; // 结束循环
}
}
return 0;
}
例题：P2240 [深基12.例1] 部分背包问题
分析：因为背包的承重量有限，如果能拿走相同重量的金币，当然是优先拿走单位价格最贵的金币。所以正确的做法是将金币的单价从高往低排序，然后按照顺序将整堆金币都放入包里。如果整堆放不进背包，就分割这一堆金币直到刚好能装下为止。
直觉是对的，但是最好证明一下。首先，所有的东西价值都是正的，因此只要金币总数足够，背包就必须要装满而不能留空；其次，利用反证法：假设没有在背包中放入单价高的金币而放入了单价更低的金币，那么就可以用等重量的更高价值金币替换掉背包里的低价值金币，那总价值反而变高了，说明原来的不是最优解，所以贪心算法成立。
#include <cstdio>
#include <algorithm>
using std::sort;
const int N = 105;
struct Coin {
int m, v; // 重量和价值
};
Coin a[N];
int main()
{
int n, t; scanf("%d%d", &n, &t);
for (int i = 1; i <= n; i++) {
scanf("%d%d", &a[i].m, &a[i].v);
}
sort(a + 1, a + n + 1, [](Coin c1, Coin c2) {
return c1.v * c2.m > c2.v * c1.m; // 按单价降序排序
});
double ans = 0;
for (int i = 1; i <= n; i++) {
if (a[i].m > t) { // 如果不够拿走整堆金币，则这就是最后一次拿
// 装下部分金币
ans += 1.0 * a[i].v / a[i].m * t;
break;
} else {
ans += a[i].v; t -= a[i].m; // 拿走整堆
}
}
printf("%.2f\n", ans);
return 0;
}
为了方便排序，定义 Coin 结构体来存储金币堆的重量和价值——性价比不需要存下来，而是在调用 sort 的时候进行判断。比较性价比时本来是判断 1.0*c1.v/c1.m>1.0*c2.v/c2.m，但是为了规避可能的浮点数计算误差，转化成乘法之后更精确，也能加快速度。
这里用的是证明贪心策略正确性的一种典型方法：假设要选择的方案不按照贪心策略，证明用这种贪心策略替换掉非贪心策略后，结果会更好（至少不会更差）。
例题：P1223 排队接水
分析：让平均时间最短等价于让所有人的等待时间和最短。由于排队接水是一个接着一个的，也就是只允许最多一个人同时打水，所以某一个人打水的时候其身后的人的等待时间总和就是每个人单独打水时间的和。第一个人不需要等待，第二个人需要等待第一个人打水的时间，第三个人需要等待前两个人打水的时间。假设经过安排后，第 \(i\) 个人的打水时间是 \(t_i\)。则所有打水人的等待时间总和为 \(s = (n-1)t_1 + (n-2)t_2 + \cdots + 1 \times t_{n-1} + 0 \times t_n\)。
可以发现，\(t_1\) 的系数较大，\(t_n\) 的系数比较小。所以可以猜到，\(t_1\) 到 \(t_n\) 应该从小到大排序，可以使时间总和 \(s\) 最小。
当然，这是可以证明的。假设最佳方案中，\(t_1\) 到 \(t_n\) 不是从小到大排序，假设存在当 \(i<j\) 时，\(t_i>t_j\)。那么这两项对于总时间的贡献是 \(s_1 = at_i + bt_j\)，其中系数 \(a>b\)。若将 \(t_i\) 和 \(t_j\) 调换，那么对总时间的贡献会变成 \(s_2 = at_j + bt_i\)，两者相减有 \(s_1 - s_2 = a(t_i - t_j) - b(t_i - t_j) = (a-b)(t_i - t_j) > 0\)，说明这样调换后总时间会缩短，也就说明原本的方式不是“最佳方案”，所以贪心算法成立。
#include <cstdio>
#include <algorithm>
using std::sort;
const int N = 1005;
struct Person {
int t, id;
};
Person a[N];
int main()
{
int n; scanf("%d", &n);
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i].t); a[i].id = i;
}
sort(a + 1, a + n + 1, [](Person p1, Person p2) {
return p1.t < p2.t;
});
double s = 0;
for (int i = 1; i <= n; i++) {
s += a[i].t * (n - i);
printf("%d ", a[i].id);
}
printf("\n%.2f\n", s / n);
return 0;
}
代码中使用了结构体来存储每个人的信息，排序时按照接水时间从小到大排序，最后计算耗时总长然后除以人数得到平均值。
例题：P4995 跳跳！
分析：不难发现，这里的贪心策略是从初始点（最左边的 0 点）跳到最右边，再跳到第二左的位置，再跳到第二右的位置，……，以此类推。
#include <cstdio>
#include <algorithm>
using std::sort;
using ll = long long; // 用ll替代long long
const int N = 305;
int h[N];
int main()
{
int n;
scanf("%d", &n);
for (int i = 1; i <= n; ++i) scanf("%d", &h[i]);
sort(h + 1, h + n + 1);
int p = 0, q = n;
int dir = 0;
ll ans = 0; // ll的范围大约是-9e18~9e18
while (p < q) {
ans += (h[q] - h[p]) * (h[q] - h[p]);
// 注意，如果相乘的两项本身都是int类型，而乘积结果可能超出int范围
// 可以写成 1ll * ... * ...，这里1ll表示ll类型下的1，它与第一项先乘可以使结果变成ll类型
// 这样再与第二项相乘时也会在ll范围下进行
if (dir == 0) p++;
else q--;
dir = 1 - dir; // 改变跳跃方向
}
printf("%lld\n", ans); // ll的输出格式符为%lld
return 0;
}
例题：P1803 凌乱的yyy / 线段覆盖
分析：如果所有的比赛时间都不冲突，那么问题就变简单了，全部参加即可。所以问题在于有些比赛时间会冲突，考虑两种情况：
- 一个比赛被另一个比赛包含：这两个比赛冲突了，要选择比赛 1，因为比赛 1 先结束，这样可能后续比赛被占用时间的可能就少一些。
- 一个比赛和另一个比赛相交：还是应该选择比赛 1，同样的道理，早结束可以减少对后续比赛的时间占用。
最先选择参加哪一场比赛呢？根据分析，应该选择最先结束的那一场比赛。接下来，要选择能够参加的比赛中，最早结束的比赛（既然已经决定参加上一场比赛了，那么所有和上一场冲突的比赛都不能参加了），直到没有比赛可以参加为止。这样可以保证不管在什么时间点之前，能够参加比赛的数量都是最多的，因此贪心算法成立。
这是证明贪心的另一种方法——数学归纳法：每一步的选择都是到当前为止的最优解，一直到最后一步就成为了全局的最优解。
#include <cstdio>
#include <algorithm>
using std::sort;
const int N = 1e6 + 5;
struct Contest {
int bg, ed;
};
Contest a[N];
int main()
{
int n;
scanf("%d", &n);
for (int i = 1; i <= n; i++) scanf("%d%d", &a[i].bg, &a[i].ed);
sort(a + 1, a + n + 1, [](Contest c1, Contest c2) {
return c1.ed < c2.ed;
});
int ans = 1;
int cur = a[1].ed; // 上一个选择的比赛的结束时间
for (int i = 2; i <= n; i++)
if (a[i].bg >= cur) { // 和上一个选择的比赛不冲突
cur = a[i].ed;
ans++;
}
printf("%d\n", ans);
return 0;
}
本题中将所有比赛的结束时间排序，然后依次进行贪心：如果能够参加这场比赛，就报名参加；如果这场比赛和上一场冲突，就放弃。贪心过程的算法时间复杂度是 \(O(n)\)，但是排序的算法复杂度可达 \(O(n \log n)\)，所以时间复杂度的瓶颈在排序上。
习题：UVA1420 Priest John's Busiest Day
解题思路
解决这个调度问题的核心在于决定处理任务的顺序，一个直观的想法是先处理那些“最紧急”的任务。那么，如何定义“紧急”呢？
一个任务的“紧急”程度，可以由它最晚必须开始的时间来衡量。如果一个任务的最晚开始时间很早，那么它就更紧急，应该优先处理它。
因为最短仪式时长必须大于婚礼总时长的一半，由于时间是整数，等价于这个最短仪式时长 \(d_i\) 等于 \(\lfloor (T_i - S_i) / 2 \rfloor + 1\)。而仪式最晚必须在 \(T_i\) 时刻结束，因此，仪式的最晚开始时间是 \(T_i - d_i\)。贪心策略就此形成：按照每个仪式“最晚开始时间”的升序来处理所有婚礼。
参考代码
#include <cstdio>
#include <algorithm>
using ll = long long;
using std::sort;
const int N = 100005;
struct Wedding { // 定义婚礼结构体
int s, t; // s：开始时间，t：结束时间
};
Wedding w[N]; // 结构体数组，存储所有婚礼信息
int main()
{
while (true) { // 循环处理多个测试用例
int n; scanf("%d", &n);
if (n == 0) break;
for (int i = 1; i <= n; i++) { // 读取 n 个婚礼的时间
scanf("%lld%lld", &w[i].s, &w[i].t);
}
// 1. 排序
sort(w + 1, w + n + 1, [](Wedding a, Wedding b) {
// 计算每个婚礼所需的最短仪式时长
int mida = (a.t - a.s) / 2 + 1;
int midb = (b.t - b.s) / 2 + 1;
// 计算每个仪式的“最晚开始时间”（deadline）
// 并按此时间的升序对婚礼进行排序
return a.t - mida < b.t - midb;
}); // 使用 lambda 表达式作为自定义比较函数
// 2. 模拟调度
int ct = w[1].s; // currentTime，记录牧师空闲下来的时刻，初始为 0
bool ok = true; // 标记调度是否可行
for (int i = 1; i <= n; i++) { // 遍历排序后的婚礼列表
ll mid = (w[i].t - w[i].s) / 2 + 1; // 计算当前婚礼所需的最短仪式时长
// 确定仪式的实际开始时间
// 必须在牧师空闲后，且在婚礼开始后
if (w[i].s > ct) ct = w[i].s;
if (ct + mid > w[i].t) { // 检查可行性：仪式结束时间是否在婚礼结束时间之前
ok = false; break; // 如果超时，则调度失败
}
ct += mid; // 更新牧师的空闲时间为本次仪式的结束时间
}
// 3. 输出结果
printf("%s\n", ok ? "YES" : "NO");
}
return 0;
}
例题：P1012 [NOIP1998 提高组] 拼数
排序策略的证明：考虑两个字符串 A 和 B
如果我们把字符串对应的十进制数看成 a 和 b，则 \(\overline{AB} > \overline{BA}\) 等价于
\(a \times 10^{\lvert B \rvert} + b > b \times 10^{|A|} + a\) 等价于
\(\frac{a}{10^{\lvert A \rvert}-1} > \frac{b}{10^{\lvert B \rvert}-1}\) 其中 |A| 和 |B| 代表字符串的长度
这说明这种比较策略具备传递性：即如果 AB 这种拼数方式优于 BA，BC 优于 CB，则最终顺序应为 ABC
#include <iostream>
#include <string>
#include <algorithm>
using std::cin;
using std::cout;
using std::sort;
using std::string;
const int N = 25;
string a[N];
int main()
{
int n;
cin >> n;
for (int i = 1; i <= n; i++) cin >> a[i];
sort(a + 1, a + n + 1, [](string s1, string s2) {
return s1 + s2 > s2 + s1;
});
for (int i = 1; i <= n; ++i) cout << a[i];
return 0;
}
习题：P1031 [NOIP 2002 提高组] 均分纸牌
解题思路
首先，计算所有纸牌的总数，然后除以牌堆数 \(N\)，得到每堆牌最终应该具有的平均数量 \(avg\)。因为题目保证总数是 \(N\) 的倍数，所以 \(avg\) 的计算可以直接整除。
可以从左到右，依次处理每一堆纸牌，让它们一堆一堆地达到平均值。
考察第 1 堆的牌数 \(A_1\)，如果它不等于 \(avg\)，那么它必须和第 2 堆进行交换才能达到平衡（因为它没有左边的牌堆）。将这个差额 \(A_1 - avg\) 从第 1 堆“转移”到第 2 堆，并记为一次移动。操作后，第 1 堆的牌数变为 \(avg\)，而第 2 堆的牌数则相应地增减。
处理第 2 堆，此时它的牌数已经吸收了来自第 1 堆的差额。再次比较此时的 \(A_2\) 和 \(avg\)，如果它们不相等，那么第 2 堆就必须和第 3 堆进行交换来达到平衡。再次记录一次移动，并将差额转移给第 3 堆。
这个过程可以一直进行下去，对于第 \(i\) 堆（\(1 \le i \lt N\)），如果它的牌数不为 \(avg\)，就将其与 \(avg\) 的差额全部转移给第 \(i+1\) 堆，并计为一次移动。
当处理完第 \(N-1\) 堆，让它通过与第 \(N\) 堆的交换达到平衡后，整个过程就结束了。因为前 \(N-1\) 堆的牌数都已经是 \(avg\)，而总牌数是固定的，所以第 \(N\) 堆的牌数必然也自动变成了 \(avg\)，无需再做任何操作。
通过这种方式可以发现，任何一堆（除了最后一堆）只要其初始（或被前面牌堆影响后）的数量不等于 \(avg\)，就必然需要进行一次移动。因此，最少的移动次数就等于在这个从左到右的调整过程中，牌数不等于 \(avg\) 的牌堆的数量。
参考代码
#include <cstdio>
const int N = 105;
int a[N]; // 存储每堆牌的数量
int main()
{
int n;
scanf("%d", &n); // 读取牌堆的数量
int sum = 0; // 用于计算总牌数
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]); // 读取每堆牌的初始数量
sum += a[i];
}
// 计算每堆牌最终应该达到的平均数量
int avg = sum / n;
int ans = 0; // 记录移动的次数
// --- 核心贪心算法 ---
// 从左到右遍历每一堆牌（除了最后一堆）
// 思想是：对于第 i 堆，如果其牌数不等于平均值，
// 那么它必须和右边的第 i+1 堆进行交换，以使自己达到平均值。
// 这个操作算作一次移动。
for (int i = 1; i < n; i++) {
// 如果第 i 堆的牌数不等于平均值
if (a[i] != avg) {
ans++; // 移动次数加 1
// 计算第 i 堆需要从第 i+1 堆得到(或给予)的牌数
int change = avg - a[i];
// 更新第 i 堆和第 i+1 堆的牌数
// a[i] 变为 avg
a[i] += change;
// a[i+1] 承担了 a[i] 的盈余或亏损，将差值传递下去
a[i + 1] -= change;
}
}
// 当循环结束时，前 n-1 堆都已达到平均值。
// 由于总牌数不变，最后一堆也必然自动达到了平均值。
// 因此，ans 就是最少的移动次数。
printf("%d\n", ans); // 输出最少移动次数
return 0;
}
正确性证明
把 \(N\) 堆牌看作 \(N-1\) 个隔断，也就是每个 \(A_i\) 和 \(A_{i+1}\) 之间有个隔断。
为了让前 \(i\) 堆（作为一个整体）最终达到平衡，它们总共应该有 \(i \cdot avg\) 张牌。设前 \(i\) 堆牌的初始总牌数为 \(sum_i = A_1 + A_2 + \cdots + A_i\)，如果 \(sum_i\) 不等于 \(i \cdot avg\)，那么这个差额必须通过第 \(i\) 堆和第 \(i+1\) 堆之间的隔断进行传递。因为前 \(i\) 堆是一个封闭的系统，它只能与第 \(i+1\) 堆交换纸牌。如果 \(sum_i \gt i \cdot avg\)，说明前 \(i\) 堆有多余的牌，必须至少向右传出 \(sum_i - i \cdot avg\) 张牌。如果 \(sum_i \lt i \cdot avg\)，说明前 \(i\) 堆有亏空，必须至少从右边拿进 \(i \cdot avg - sum_i\) 张牌。只要 \(sum_i \ne i \cdot avg\)，就意味着在第 \(i\) 堆和第 \(i+1\) 堆之间必然发生了至少一次移动。
而上面的算法在第 \(i\) 步决定是否要移动的条件是 \(A_i \ne avg\)，在算法执行到第 \(i\) 步时，它已经保证了前 \(i-1\) 堆的牌数都是 \(avg\)。此时，前 \(i\) 堆的总牌数是 \((i-1) \cdot avg + A_i\)，因此这个条件实际上和上面说的 \(sum_i \ne i \cdot avg\) 是等价的。
这样就证明了，对于任何一个 \(i\)（从 \(1\) 到 \(N-1\)），如果前 \(i\) 堆的初始总牌数不等于 \(i \cdot avg\)，那么在第 \(i\) 堆和第 \(i+1\) 堆之间就至少需要一次移动，这些移动需求是相互独立的（在第 1 和第 2 堆之间的移动无法弥补第 2 和第 3 堆之间的不平衡）。
因此，最少的总移动次数至少是满足 \(sum_i \ne i \cdot avg\) 的 \(i\) 的数量。
上面的贪心算法恰好在且仅在 \(sum_i \ne i \cdot avg\) 时增加一次移动计数，所以，它计算出的移动次数恰好等于这个理论上的最小值。
综上所述，该贪心策略是正确的，且能得到最优解。
习题：P3817 小A的糖果
解题思路
先考虑单独一个糖果盒，如果一个糖果盒里糖果数量就超出限制了，那当然首先要将其吃到剩 x 个。接下来考虑相邻两个糖果盒，从第一个糖果盒和第二个糖果盒开始考虑，假如两个相邻糖果盒中糖果数量加起来超了，不管是吃第一个糖果盒里的还是第二个糖果盒里的，需要吃的数量是一样的。如果我们吃第一个糖果盒中的糖果，那么它只能保证前两个糖果盒中糖果总量不超限，对第二和第三个糖果盒的情况没有影响，而如果我们选择吃第二个糖果盒中的糖果，那么既能使得前两个糖果盒糖果总数不超限，又能够同时减少一点第二盒与第三盒形成的总数。所以我们吃靠后的那个。将这个处理方式继续往右边类推即可。
#include <cstdio>
using ll = long long;
const int N = 1e5 + 5;
int a[N];
int main()
{
int n, x; scanf("%d%d", &n, &x);
ll ans = 0;
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]);
if (a[i] > x) {
ans += a[i] - x;
a[i] = x;
}
}
for (int i = 2; i <= n; i++) {
int diff = a[i - 1] + a[i] - x;
if (diff > 0) {
ans += diff;
a[i] -= diff;
}
}
printf("%lld\n", ans);
return 0;
}
习题：P1478 陶陶摘苹果（升级版）
解题思路
相当于前面“奶牛塔”那题，优先摘花费力气少的，只不过是要建立在能够到的基础上。
#include <cstdio>
#include <algorithm>
using std::sort;
const int N = 5005;
struct Apple {
int x, y;
};
Apple ap[N];
int main()
{
int n, s, a, b; scanf("%d%d%d%d", &n, &s, &a, &b);
for (int i = 1; i <= n; i++) {
scanf("%d%d", &ap[i].x, &ap[i].y);
}
sort(ap + 1, ap + n + 1, [](Apple a1, Apple a2) {
return a1.y < a2.y;
});
int ans = 0;
for (int i = 1; i <= n; i++) {
if (ap[i].y > s) break; // 剩余的力气已经不足以摘接下来的苹果了
if (a + b >= ap[i].x) { // 够得到才能摘
ans++; s -= ap[i].y;
}
}
printf("%d\n", ans);
return 0;
}
习题：P1208 [USACO1.3] 混合牛奶 Mixing Milk
解题思路
优先采购单价便宜的牛奶，如果把某款牛奶采购进来还没达到需要的量，就全买进，如果全买进来超了，就买还缺的部分然后结束。
#include <cstdio>
#include <algorithm>
using std::sort;
const int M = 5005;
struct Milk {
int p, a;
};
Milk a[M];
int main()
{
int n, m; scanf("%d%d", &n, &m);
for (int i = 1; i <= m; i++) {
scanf("%d%d", &a[i].p, &a[i].a);
}
// 按单价从小到大排序
sort(a + 1, a + m + 1, [](Milk m1, Milk m2) {
return m1.p < m2.p;
});
int ans = 0;
for (int i = 1; i <= m; i++) {
if (a[i].a >= n) { // 买最后一点就够了
ans += n * a[i].p; break;
} else { // 整批买进
ans += a[i].a * a[i].p;
n -= a[i].a;
}
}
printf("%d\n", ans);
return 0;
}
习题：P1094 [NOIP2007 普及组] 纪念品分组
解题思路
按纪念品价格从小到大排序，考虑到每个分组最多两件，尽量考虑搭配一大一小。
- 如果当前最便宜的和最贵的打包到一起超限了，那么最贵的只能自成一组（连最便宜的都不能合一组，更不用说其他的了）
- 如果最便宜的和最贵的可以一起打包，那就让它们两个打包一组（理论上此时最贵的可能可以不找最便宜的一起打包，但是不影响）
重复以上过程，完成对所有纪念品的分组。
#include <cstdio>
#include <algorithm>
using std::sort;
const int N = 30005;
int a[N];
int main()
{
int w, n; scanf("%d%d", &w, &n);
for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);
sort(a + 1, a + n + 1);
int l = 1, r = n;
int ans = 0;
while (l <= r) {
if (l == r) { // 还剩最后一件
ans++;
break;
} else {
// 给最贵的分组，如果能搭个最便宜的就搭一下，不然就自成一组
if (a[l] + a[r] <= w) l++;
r--; ans++;
}
}
printf("%d\n", ans);
return 0;
}
习题：P1181 数列分段 Section I
解题思路
由于连续性的约束，不能打乱数字的顺序，只能在数字之间进行“切割”来分段。为了让段数最少，应该让每一段尽可能地“长”，即包含尽可能多的数字。
这个问题可以用一个非常直观的贪心策略来解决：从数列的第一个数开始，建立一个“当前段”。依次向后读取下一个数，对于每一个新读入的数，都贪心地尝试将它加入到“当前段”中。在加入之前，检查“当前段”的和加上这个新数后，是否会超过 \(M\)。如果不超过 \(M\)，说明这个数可以安全地放入当前段，就把它加进去，更新当前段的和，然后继续处理下一个数。如果超过 \(M\)，说明这个数无法再放入当前段了，当前段的构建就此结束，必须开启一个新的段，而这个新读入的数就成为这个新段的第一个元素。同时，总的段数需要加一。重复这个过程，直到处理完所有数字。
这个贪心策略是正确的，因为为了使总段数最少，每一步都应该尽可能地延长当前段，而不是过早地开启一个新段。只有在“不得不”的情况下（即再加一个数就会超限），才开启新段。
参考代码
#include <cstdio>
int main()
{
int n, m; scanf("%d%d", &n, &m); // n：数列长度，m：每段和的最大值
int sum = 0; // 用于记录当前这一段的和
int ans = 1; // ans 用于记录段数，初始化为 1，因为只要有数字，就至少有 1 段
for (int i = 1; i <= n; i++) { // 循环读取 n 个数
int x; scanf("%d", &x); // 读取当前的数字 x
// 贪心策略：判断将当前数字 x 加入到当前段后，和是否会超过 m
if (sum + x <= m) {
sum += x; // 如果没有超过 m，则将 x 加入当前段，并更新当前段的和
} else {
// 如果加上 x 就会超过 m，说明当前段就此结束，必须开始一个新段
// 开启一个新段，新段的和从当前的数字 x 开始
sum = x;
ans++; // 总段数加 1
}
}
printf("%d\n", ans); // 输出最终的段数
return 0;
}
习题：P9749 [CSP-J 2023] 公路
解题思路
从左到右考虑，当行驶到下一个加油站时发现剩余的油不够了，相当于之前油没加够，由于油箱容量是无限大的，因此可以追溯到到目前为止的加油站里最便宜的那个，把缺的油在那个站里补上。
注意，因为买油只能买整数升，所以不妨在处理过程中维护当前油箱中的油还够车开多少里程，这样能够规避掉涉及小数的运算。
参考代码
#include <cstdio>
#include <algorithm>
using std::min;
using ll = long long;
const int N = 100005;
int v[N], a[N];
int main()
{
int n, d; scanf("%d%d", &n, &d);
for (int i = 1; i <= n - 1; i++) scanf("%d", &v[i]);
for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
int rest = 0, min_price = 0; // rest表示油箱中的油够开多少距离
ll ans = 0;
for (int i = 1; i <= n - 1; i++) {
// 到目前这个加油站为止，最便宜的油价是多少
if (min_price == 0) min_price = a[i];
else min_price = min(min_price, a[i]);
if (rest >= v[i]) {
rest -= v[i];
} else {
int need = (v[i] - rest + d - 1) / d; // 计算需要买几升油
ans += 1ll * need * min_price;
rest = rest + need * d - v[i];
}
}
printf("%lld\n", ans);
return 0;
}
习题：P1190 [NOIP 2010 普及组] 接水问题
解题思路
总耗时取决于最后一个完成接水的同学是什么时候完成的，为了让这个时间点尽可能早，应该采取一个贪心策略：每当一个水龙头空闲下来时，立即让队伍中最靠前的同学去接水。
可以用一个长度为 \(m\) 的数组 \(t\) 来维护每个水龙头下一次空闲的时刻。
最开始，第 \(1\) 到 \(m\) 号同学分别占据 \(m\) 个水龙头。对于第 \(i\) 个水龙头（\(1 \le i \le m\)），它将在 \(w_i\) 秒后变为空闲。所以，初始化 \(t_i \leftarrow w_i\)。
接着，从第 \(m+1\) 号同学开始处理，直到第 \(n\) 号同学。对于每一个新来的同学 \(i\)（\(i \gt m\)），需要决定其应该去哪个水龙头。根据贪心策略，应该去那个最早会变空闲的水龙头。遍历 \(t\) 数组，找到其中值最小的那个元素 \(t_j\)，这表示第 \(j\) 个水龙头是最早空闲的。让同学 \(i\) 去第 \(j\) 个水龙头接水，这个水龙头新的空闲时刻将变为 \(t_j + w_i\)（即在原有的任务结束后，再加上新同学的接水时间），更新 \(t_j\) 的值为 \(t_j + w_i\)。
当所有 \(n\) 个同学都被分配过之后，\(t\) 数组中的值代表了每个水龙头完成所有分配给它的任务后的最终时刻。整个接水过程的结束时间，就是所有水龙头中最晚结束工作的那个时间。因此，最终答案就是 \(t\) 数组中的最大值。
参考代码
#include <cstdio>
const int N = 1e4 + 5;
const int M = 105;
// w 数组存储每个学生的接水量，t 数组模拟每个水龙头，记录其完成当前所有任务的时刻
int w[N], t[M];
int main()
{
// n 表示学生人数，m 表示水龙头个数
int n, m; scanf("%d%d", &n, &m);
// 循环读入每个学生的接水量
for (int i = 1; i <= n; i++) {
scanf("%d", &w[i]);
// 如果是前 m 个学生，他们直接占据一个水龙头
if (i <= m) {
// 第 i 个水龙头的完成时间就是第 i 个学生的接水时间
t[i] = w[i];
}
}
// 模拟剩下的学生 (从第 m+1 个到第 n 个)
for (int i = m + 1; i <= n; i++) {
// 寻找最早完成接水的水龙头
int j = 1; // 假设第一个水龙头最早完成
// 遍历所有水龙头，找到真正最早完成的那个
for (int k = 2; k <= m; k++) {
// 如果发现有其他水龙头比当前记录的水龙头更早完成
if (t[k] < t[j]) {
// 更新 j 为这个更早完成的水龙头的编号
j = k;
}
}
// 将当前学生 i 分配给最早完成的水龙头
// 更新这个水龙头的总耗时
t[j] += w[i];
}
// 寻找所有水龙头中，最晚的完成时间
int ans = t[1]; // 假设第一个水龙头的完成时间是最终答案
// 遍历所有水龙头，找到真正的最晚完成时间
for (int i = 2; i <= m; i++) {
if (t[i] > ans) {
ans = t[i];
}
}
// 输出最终答案
printf("%d\n", ans);
return 0;
}
习题：CF2121B Above the Clouds
解题思路
\(s = a + b + c\) 且 \(a,b,c\) 都非空，这意味着 \(b\) 必须是 \(s\) 的一个真子串，并且不能是 \(s\) 的前缀或后缀。换句话说，\(b\) 必须完全位于 \(s\) 的“中间”部分，不能包含 \(s\) 的第一个或最后一个字符。\(b\) 是 \(a+c\) 的子串，\(a+c\) 其实就是把 \(s\) 中间属于 \(b\) 的那部分挖掉后，剩下两头拼接起来的结果。
考虑最简单的情况：如果 \(b\) 只是一个单字符的字符串，问题会怎样？假设选择 \(b\) 为 \(s\) 中间部分的某个字符 \(s_i\)（其中 \(2 \le i \le n-1\)，\(n\) 是字符串长度），根据这个选择，\(a\) 就是 \(s\) 在 \(s_i\) 之前的部分 \(s_{1 \dots i-1}\)，\(c\) 就是 \(s\) 在 \(s_i\) 之后的部分 \(s_{i+1 \dots n}\)。因为 \(i\) 不在两端，所以 \(a\) 和 \(c\) 必定非空，满足了条件。现在，需要判断 \(b\)（即 \(s_i\)）是否是 \(a+c\) 的子串，\(a+c\) 就是 \(s\) 字符串挖掉 \(s_i\) 之后的结果。所以，问题就转化为：字符 \(s_i\) 是否在 \(s\) 的其他位置也出现过？换句话说，字符 \(s_i\) 在整个字符串 \(s\) 中的总出现次数是否大于 \(1\)？
如果能在 \(s\) 的中间部分（\(s_{2 \dots n-1}\)）找到任何一个字符 \(s_i\)，它在整个 \(s\) 中的出现次数大于 \(1\)，那么就可以构造出一组解。令 \(b = s_i\)，\(a\) 和 \(c\) 分别是 \(s_i\) 前后的部分。因为 \(s_i\) 在 \(s\) 中还有其他出现位置，那个位置必然落在 \(a\) 或 \(c\) 中，所以 \(b\) 一定是 \(a+c\) 的子串，因此答案是 Yes。
反过来，如果 \(s\) 中间部分（\(s_{2 \dots n-1}\)）的所有字符，在整个 \(s\) 中都只出现了唯一一次。那么无论如何选取中间的子串 \(b\)，\(b\) 中的每个字符在整个 \(s\) 中都是独一无二的。而 \(a+c\) 是由 \(s\) 中不属于 \(b\) 的部分构成的，所以 \(a+c\) 中不可能包含 \(b\) 中的任何字符。因此 \(b\) 就不可能是 \(a+c\) 的子串，这种情况下无解，答案是 No。
综上所述，问题被简化为：是否存在一个位于 \(s_{2 \dots n-1}\) 的字符，该字符在整个字符串 \(s\) 中不止出现一次？
参考代码
#include <iostream>
#include <string>
using namespace std;
// 全局数组，用于统计 'a' 到 'z' 每个字符的出现次数
int cnt[26];
void solve() {
// 每次处理新的测试用例前，清空计数数组
for (int i = 0; i < 26; i++) cnt[i] = 0;
int n; string s;
cin >> n >> s; // 读入字符串长度 n 和字符串 s
// 第一步：遍历整个字符串，统计每个字符的频率
for (char ch : s) {
cnt[ch - 'a']++;
}
// 第二步：遍历字符串的“中间部分”（不包括第一个和最后一个字符）
// 索引从 1 到 n-2
for (int i = 1; i < n - 1; i++) {
char ch = s[i];
// 检查当前中间字符 ch 在整个字符串中的出现次数
if (cnt[ch - 'a'] > 1) {
// 如果次数大于1，说明找到了一个有效的分割方案
// (b = ch, a = s的前缀, c = s的后缀)
cout << "Yes\n"; // 输出 "Yes"
return; // 结束当前测试用例的处理
}
}
// 如果循环结束都没有找到满足条件的中间字符，则说明无解
cout << "No\n";
}
int main()
{
int t;
cin >> t; // 读入测试用例的数量
for (int i = 1; i <= t; i++) { // 循环处理每个测试用例
solve();
}
return 0;
}
习题：CF2050B Transfusion
解题思路
题目给出的操作是：选择一个中间位置 \(i\)（\(2 \le i \le n-1\)），然后可以在 \(a_{i-1}\) 和 \(a_{i+1}\) 之间转移数值（一个加 1，另一个减 1）。
这个操作的关键在于，它只在索引 \(i-1\) 和 \(i+1\) 之间移动数值，这两个索引的奇偶性是相同的（同为奇数或同为偶数）。通过连续应用这个操作，比如在 \(i=2\) 时操作 \(a_1\) 和 \(a_3\)，在 \(i=4\) 是操作 \(a_3\) 和 \(a_5\)，可以发现，数值可以在所有奇数索引的元素之间自由流动。同理，数值也可以在所有偶数索引的元素之间自由流动。但是，没有任何操作可以把数值从一个奇数索引的元素移动到一个偶数索引的元素上，反之亦然。
基于以上分析，可以发现两个“不变量”：所有位于奇数/偶数索引位置上的元素之和是恒定的。
这意味着，奇数位和偶数位是两个独立的、封闭的系统。
目标是让数组中所有 \(n\) 个元素都相等，变成同一个值 \(X\)。如果奇数位的元素们可以被平均分配，那么它们最终都会变成 \(X\)。这要求它们的总和必须能被奇数位的元素个数整除，并且商必须等于 \(X\)。同理，偶数位的元素们也必须能被平均分配，它们最终也都会变成 \(X\)。这要求它们的总和必须能被偶数位的元素个数整除，并且商必须等于 \(X\)。
因此，要判断是否能让所有元素相等，只需要检查以下两个条件：
- 整除性：奇数位的总和必须能被奇数位的个数整除。并且，偶数位的总和必须能被偶数位的个数整除。如果任意一个不满足，就不可能实现平均分配，答案为 NO。
- 均值相等：在满足整除性的前提下，计算出奇数位的平均值和偶数位的平均值。这两个独立的系统要统一成一个值，就必须要求它们的平均值相等。如果相等，答案为 YES；如果不等，答案为 NO。
参考代码
#include <cstdio>
using ll = long long;
void solve() {
int n; scanf("%d", &n);
ll s1 = 0, s0 = 0;
int c1 = 0, c0 = 0;
for (int i = 1; i <= n; i++) {
int x;
scanf("%d", &x);
if (i % 2 == 1) {
s1 += x; c1++;
} else {
s0 += x; c0++;
}
}
if (s1 % c1 != 0 || s0 % c0 != 0) {
printf("NO\n"); return;
}
s1 /= c1; s0 /= c0;
if (s0 == s1) {
printf("YES\n");
} else {
printf("NO\n");
}
}
int main()
{
int t; scanf("%d", &t);
for (int i = 1; i <= t; i++) {
solve();
}
return 0;
}
习题：P9515 「JOC-1A」限时签到
解题思路
由于每个 \(x_i \le f\)，每个签到处都是“顺路”的，在行进过程中没有必要折返。
如果一个签到处的 \(a_i + f - x_i \gt t\)，说明这个签到处无论如何也签不上，因为签完它会使得来不及赶到目的地。
考虑每一个不会导致来不及的签到处，如果到达它时它还没营业，那就等到它营业，这不会导致后面本来能签上的签到处签不上了，这也就意味着每个签到处能否成功签到是完全独立的。
因此实现时不需要开任何数组，直接循环读取每个签到处的位置和营业时间，读取完立马判断能否完成签到。
参考代码
#include <cstdio>
using ll = long long;
int main()
{
int n;
ll t, f;
scanf("%d%lld%lld", &n, &t, &f);
int ans = 0;
for (int i = 1; i <= n; i++) {
ll x, a;
scanf("%lld%lld", &x, &a);
if (a + f - x <= t) {
ans++;
}
}
printf("%d\n", ans);
return 0;
}
习题：P5019 [NOIP2018 提高组] 铺设道路
解题思路
初步想法是每次都找到当前最深的坑，然后以它为中心向两边扩展，形成一个最长的、全都不为 0 的区间，然后填一次，这个思路比较复杂。
换个角度思考，总共需要填多少次？从左到右遍历道路，看看在每个位置 \(i\)，必须新开始多少次填补操作。
对于第 1 块区域 \(d_1\)，它需要被填 \(d_1\) 次。由于它左边没有区域，这 \(d_1\) 次操作都必须从这里开始。所以，至少需要 \(d_1\) 次操作。可以认为，启动了 \(d_1\) 个填补操作，它们都覆盖了位置 1。
对于第 2 块区域 \(d_2\)，它需要被填 \(d_2\) 次。如果 \(d_2 \le d_1\)，在处理 \(d_1\) 时启动的 \(d_1\) 次操作，可以“顺便”把 \(d_2\) 也填了。因为 \(d_2\) 的需求比 \(d_1\) 少，所以这 \(d_1\) 次操作足够满足 \(d_2\) 的需求。因此，在位置 2，不需要新开始任何操作。而如果 \(d_2 \gt d_1\)，在处理 \(d_1\) 时启动的 \(d_1\) 次操作，只能满足 \(d_2\) 的前 \(d_1\) 次填补需求。\(d_2\) 仍然还差 \(d_2 - d_1\) 次填补。由于位置 1 此时已经被被填平了，这剩下的 \(d_2 - d_1\) 次操作必须是新开始的，它们的作用范围至少要从位置 2 开始。
推广到第 \(i\) 块区域 \(d_i\)，它左边的区域 \(d_{i-1}\) 已经“预订”了 \(d_{i-1}\) 次可以延伸过来的填补操作。如果 \(d_i \le d_{i-1}\)，那么 \(d_i\) 的所有填补需求都可以被左边延伸过来的操作“顺便”满足，不需要为 \(d_i\) 开启新的操作。如果 \(d_i \gt d_{i-1}\)，那么 \(d_i\) 只有 \(d_{i-1}\) 的深度可以被“顺便”填平，还剩下 \(d_i - d_{i-1}\) 的深度需要额外的、新开始的操作来填补。
参考代码
#include <cstdio>
#include <algorithm>
using std::max;
const int N = 100005;
int d[N]; // 存储每块区域的下陷深度
int main()
{
int n;
scanf("%d", &n); // 读取道路的长度 n
// 循环读取 n 个区域的初始深度
// d[0] 会被默认初始化为 0，这正好符合贪心策略
for (int i = 1; i <= n; ++i) {
scanf("%d", &d[i]);
}
int ans = 0; // 用于累计总天数（总操作次数）
// 核心贪心算法
for (int i = 1; i <= n; ++i) { // 遍历每一块区域，计算在该区域必须“新开始”的操作次数
// 如果当前区域的深度 d[i] 大于前一个区域的深度 d[i-1]
// 说明从前一个区域延伸过来的操作不足以填平当前区域
// 差值 d[i] - d[i-1] 就是必须在当前区域或之后新开始的操作次数
// 如果 d[i] <= d[i-1]，说明前一个区域的操作足够覆盖当前区域
// 不需要新开始操作，贡献为 0
ans += max(d[i] - d[i - 1], 0);
}
printf("%d\n", ans); // 输出最终结果
return 0;
}
习题：P1209 [USACO1.3] 修理牛棚 Barn Repair
解题思路
如果只有一块木板，那么木板的长度就是最前最后两头牛的编号差加 1。
而题目允许最多使用 \(m\) 块木板，就相当于可以在整块木板上制造 \(m-1\) 个“断点”。每一个断点都意味着可以跳过两个牛棚之间的一段空隙，从而节省木板长度。
如何最优化？为了让节省的木板长度最多，应该把这 \(m-1\) 个宝贵的“断点”放在最大的 \(m-1\) 个空隙处。
参考代码
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 205;
int id[N]; // 存储每头牛所在牛棚的编号
int d[N]; // 存储排序后相邻有牛牛棚之间的距离
/**
* @brief 主函数，解决修理牛棚问题
*
* 核心思路：贪心算法
* 1. 首先，假设只用一块最长的木板覆盖所有牛棚，其长度为 (最后一头牛的位置 - 第一头牛的位置 + 1)。
* 2. 最多有 m 块木板，这意味着可以在木板之间形成 m-1 个“断点”或“间隙”。
* 3. 为了使总长度最小，应该将这些“断点”放在牛与牛之间最大的 m-1 个空隙处。
* 4. 每在一个空隙处断开，就能省去这段空隙的长度。一个距离为 D 的空隙（如牛棚3和牛棚8，D=5），
* 可以节省 D-1 的木板长度（即跳过牛棚4,5,6,7，节省长度4）。
* 5. 算法流程：计算出所有相邻牛之间的距离，将这些距离从大到小排序，
* 然后从初始总长度中减去前 m-1 个最大距离所能节省的长度。
*/
int main()
{
int m, s, c; // m: 最大木板数, s: 牛棚总数, c: 牛的总数
scanf("%d%d%d", &m, &s, &c);
// 读取 c 头牛各自所在的牛棚编号
for (int i = 1; i <= c; i++) {
scanf("%d", &id[i]);
}
// 特殊情况处理：如果木板数足够或超过牛的数量，
// 那么最优解是为每头牛都用一块长度为1的木板。
if (m >= c) {
printf("%d", c);
return 0;
}
// 将牛棚编号从小到大排序，这是计算空隙和初始长度的前提。
sort(id + 1, id + c + 1);
// 计算初始总长度：假设只用一块长木板覆盖从第一头牛到最后一头牛的所有牛棚。
int ans = id[c] - id[1] + 1;
// 计算 c-1 个相邻有牛牛棚之间的距离。
// 例如，牛在牛棚3和牛棚8，距离 d[i] = 8 - 3 = 5。
for (int i = 1; i < c; i++) {
d[i] = id[i + 1] - id[i];
}
// 将所有距离从大到小排序，这样就能优先在最大的空隙处“断开木板”。
sort(d + 1, d + c, [](int x, int y) {
return x > y;
});
// 贪心核心：有 m 块木板，可以形成 m-1 个断点。
// 在 m-1 个最大的空隙处断开，可以最大化节省的木板长度。
for (int i = 1; i < m; i++) {
// 如果距离为1（d[i]==1），说明牛棚是连续的，空隙为0。
// 因为距离已经从大到小排序，后续的距离只会更小或相等，节省的长度为0或负数（不可能），提前结束。
if (d[i] <= 1) break;
// 每断开一个距离为 d[i] 的空隙，可以节省 (d[i] - 1) 的长度。
// 例如，牛棚8和10之间距离是2，断开后省掉牛棚9，节省长度为1。
ans -= (d[i] - 1);
}
// 输出最终的最小总长度
printf("%d", ans);
return 0;
}
习题：P11205 「Cfz Round 9」Hope
解题思路
这道题的目标是通过一次操作，使得所有花瓣堆中，未出现的最小正整数（也称为 MEX，Minimum EXcluded value）尽可能大。
为了让这个值（称之为 \(k\)）最大化，应该努力让 \(1, 2, 3, \dots, k-1\) 这些数量的花瓣堆都存在。这引导出一个贪心策略：按顺序（从 \(1\) 开始）构造连续的整数花瓣堆。
首先，将所有花瓣堆按花瓣数量从小大排序。这有助于按顺序处理，做出最优的局部决策。
维护一个目标值 \(cur\)，初始为 \(1\)，\(cur\) 代表当前希望得到（或者说凑出）的花瓣数量。遍历排序后的花瓣堆 \(a\)：
- \(a_i = cur\)：需要的 \(cur\) 已经存在了，不需要做任何操作，直接将目标值更新为 \(cur+1\)，去寻找下一个数。
- \(a_i \gt cur\)：没有 \(cur\)，但是有比 \(cur\) 大的堆 \(a_i\)。可以从 \(a_i\) 中拿出 \(a_i - cur\) 片花瓣，使这个堆的大小恰好变为 \(cur\)，这样就成功构造出了 \(cur\)。拿出的 \(a_i - cur\) 片花瓣可以存起来，用于最后组成一个全新的堆。然后，将目标值更新为 \(cur+1\)。
- \(a_i \lt cur\)：这个堆 \(a_i\) 的花瓣数比当前需要的小，它无法变成 \(cur\)。因此，它对于构造 \(cur\) 来说是“多余”的。但是，可以从中拿出 \(a_i - 1\) 片花瓣（题目要求不能拿光），存起来用于最后组成新堆。注意，这部分并不是必须拿的，所以需要用另一个变量将这部分可用可不用的花瓣存起来。此时，由于还没找到 \(cur\)，所以 \(cur\) 的值保持不变。
在上述过程中，用两个变量来收集所有拿出的花瓣：
- \(sum\) 用于存储所有从 \(a_i \gt cur\) 的堆中拿出的花瓣（必须拿）
- \(tmp\) 用于存储所有从 \(a_i \lt cur\) 的堆中拿出的花瓣（这部分拿多少可以自由选择）
遍历完所有原始的花瓣堆后，已经通过修改（或者直接使用）原始堆，成功地凑出了 \(1, 2, \dots，cur-1\)。此时，缺失的最小正整数是 \(cur\)。现在，可以把所有收集到的花瓣拿出来组成一个全新的堆，这个新堆的大小是个范围 \([sum, sum+tmp]\)。如果 \(cur\) 在这个范围内，那么这个缺口就能补上，缺失的最小正整数变成了 \(cur+1\)。
参考代码
#include <cstdio>
#include <algorithm>
using namespace std;
using ll = long long;
const int N = 1e5 + 5;
int a[N]; // 存储每堆花瓣的数量
void solve() {
int n;
scanf("%d", &n); // 读入花瓣堆数
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]); // 读入每堆花瓣的数量
}
sort(a + 1, a + n + 1); // 将花瓣数量从小到大排序
ll sum = 0, tmp = 0; // sum: 从 >cur 的堆中拿出的花瓣; tmp: 从 <cur 的堆中拿出的花瓣
int cur = 1; // cur 是当前想要凑出的目标数量，从 1 开始
// 遍历所有排好序的花瓣堆
for (int i = 1; i <= n; i++) {
if (a[i] < cur) {
// 当前堆太小，无法凑出 cur
// 可以从中拿出 a[i]-1 片花瓣（不能拿光）备用
tmp += a[i] - 1;
} else if (a[i] == cur) {
// 恰好有大小为 cur 的堆，直接满足条件
// 目标更新为下一个整数
cur++;
} else { // a[i] > cur
// 当前堆太大，可以把它变成 cur
// 从中拿出 a[i]-cur 片花瓣，加入 sum 池
sum += (a[i] - cur);
// 成功凑出 cur，目标更新为下一个整数
cur++;
}
}
// 经过上面的循环，已经凑齐了 1, 2, ..., cur-1
// 此时，最小的缺失数是 cur
// 需要判断，用所有收集到的花瓣组成的新堆，其大小是否组成 cur
// 如果是，就能补上 cur，答案就变成 cur+1
if (sum <= cur && sum + tmp >= cur) {
cur++;
}
printf("%d\n", cur); // 输出最终答案
}
int main()
{
int t; scanf("%d", &t); // 读入测试数据组数
for (int i = 1; i <= t; i++) {
solve(); // 对每组数据调用解决函数
}
return 0;
}
习题：P1056 [NOIP 2008 普及组] 排座椅
解题思路
解决这个问题的关键突破口在于一个重要的观察：横向通道的选择和纵向通道的选择是完全独立的。
- 一条位于第 \(i\) 行和第 \(i+1\) 行之间的横向通道，只能隔开那些一个在第 \(i\) 行、另一个在第 \(i+1\) 行的“上下相邻”的学生对，它对“左右相邻”的学生对没有任何影响。
- 同理，一条位于第 \(j\) 列和第 \(j+1\) 列之间的纵向通道，只能隔开那些一个在第 \(j\) 列、另一个在第 \(j+1\) 列的“左右相邻”的学生对，它对“上下相邻”的学生对没有任何影响。
基于这个发现，可以把原问题分解为两个独立的、更简单的子问题：
- 在 \(M-1\) 个可能的横向位置中，找出 \(K\) 个位置来放置通道，使得被隔开的“上下相邻”的学生对最多。
- 在 \(N-1\) 个可能的纵向位置中，找出 \(L\) 个位置来放置通道，使得被隔开的“左右相邻”的学生对最多。
显然这两个子问题都可以用贪心算法来解决，在读入学生对的时候，顺便更新在其对应的横向或纵向位置放置通道产生的“价值”，于是问题就转化为取价值最大的若干个通道。
参考代码
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 1005;
// cnt1[i]: 在第 i 行和 i+1 行之间设置通道能隔开的学生对数（即该位置的“价值”）
int cnt1[N];
// cnt2[j]: 在第 j 列和 j+1 列之间设置通道能隔开的学生对数
int cnt2[N];
// used[i]: 在 find_best 函数中临时标记第 i 个位置是否已被选择
bool used[N];
int main()
{
int m, n, k, l, d;
// m行, n列, k个横向通道, l个纵向通道, d对交谈学生
scanf("%d%d%d%d%d", &m, &n, &k, &l, &d);
// --- 步骤1: 统计每个可能通道位置的“价值” ---
for (int i = 1; i <= d; i++) {
int x, y, p, q; // (x,y) 和 (p,q) 是交谈学生的坐标
scanf("%d%d%d%d", &x, &y, &p, &q);
if (x == p) { // 两人在同一行，说明是左右相邻
// 需要用纵向通道隔开，通道在 min(y, q) 和 min(y, q)+1 列之间
// 因此，在 min(y, q) 位置设置纵向通道的价值加一
cnt2[min(y, q)]++;
} else { // 两人在同一列，说明是上下相邻 (题目保证只有这两种情况)
// 需要用横向通道隔开，通道在 min(x, p) 和 min(x, p)+1 行之间
// 因此，在 min(x, p) 位置设置横向通道的价值加一
cnt1[min(x, p)]++;
}
}
// --- 步骤2: 定义一个通用的贪心选择函数 ---
// 使用 C++11 的 lambda 表达式，方便代码复用
// chosen: 需要选择的通道数量 (k 或 l)
// len: 总行数或列数 (m 或 n)，可能的位置有 len-1 个
// cnt: 对应的价值数组 (cnt1 或 cnt2)
auto find_best = [&](int chosen, int len, int cnt[N]) {
// 重置标记数组，为本次选择做准备
for (int i = 1; i < len; i++) used[i] = false;
// 贪心选择 'chosen' 次，每次选出当前最优的一个
for (int i = 1; i <= chosen; i++) {
int best = -1; // 记录当前找到的最佳位置的索引
// 遍历所有可能的位置，找到价值最大且未被选择的那个
for (int j = 1; j < len; j++) {
if (!used[j] && (best == -1 || cnt[j] > cnt[best])) {
best = j;
}
}
used[best] = true; // 标记该位置为已选择，下次不再考虑
}
// --- 步骤3: 按升序输出所有被选中的位置 ---
// 因为遍历是从 1 到 len-1，所以输出自然是升序的
for (int i = 1; i < len; i++) {
if (used[i]) {
printf("%d ", i);
}
}
printf("\n");
};
// --- 分别对横向和纵向通道求解并输出 ---
// 求解 k 个最佳横向通道位置
find_best(k, m, cnt1);
// 求解 l 个最佳纵向通道位置
find_best(l, n, cnt2);
return 0;
}
习题：CF2121C Those Who Are With Us
解题思路
令原始矩阵中的最大值为 \(M\)，操作是减 1，所以操作后的新最大值不可能比 \(M\) 大。最多只能将元素值减 1，所以新最大值也不可能比 \(M-1\) 小。因此，最终的答案只有两种可能：\(M\) 或者 \(M-1\)。
问题就变成了：能否通过一次操作，使得最终的最大值变成 \(M-1\)？
要让最大值变成 \(M-1\)，一个必要且充分的条件是：所有原始值为 \(M\) 的单元格都必须被操作所影响（即它们的值都被减了 1）。一个单元格 \((i,j)\) 被影响，当且仅当它位于选择的行 \(r\) 或列 \(c\) 中，即 \(i=r\) 或 \(j=c\)。
所以，问题最终转化为：是否存在这样一对 \((r,c)\)，使得所有值为 \(M\) 的单元格都位于第 \(r\) 行或第 \(c\) 列？称这样的一对 \((r,c)\) 覆盖了所有最大值单元格。
可以通过遍历来验证是否存在这样的一对 \((r,c)\)。
第一次遍历矩阵，找到最大值 \(M\)。第二次遍历矩阵，找出所有值为 \(M\) 的单元格，并进行统计：用 \(cnt\) 代表值为 \(M\) 的单元格总数，\(x_i\) 表示第 \(i\) 行中值为 \(M\) 的单元格数量，\(y_j\) 表示第 \(j\) 列中值为 \(M\) 的单元格数量。
遍历所有可能的 \((r,c)\) 组合（\(r\) 从 \(1\) 到 \(n\)，\(c\) 从 \(1\) 到 \(m\)），对于每一个组合，计算它能覆盖多少个值为 \(M\) 的单元格。覆盖的数量等于第 \(r\) 行的 \(M\) 数量加上第 \(c\) 列的 \(M\) 数量，这里需要注意，如果单元格 \((r,c)\) 本身的值就是 \(M\)，那么它在行和列中被重复计数了一次，需要减掉。如果这个覆盖数等于 \(M\) 的总数 \(cnt\)，说明找到了一个可以覆盖所有最大值的 \((r,c)\) 组合。那么答案就是 \(M-1\)，可以直接输出并结束。
如果在遍历完所有的 \((r,c)\) 组合后都未能找到一个能完全覆盖的，说明无法让所有 \(M\) 都减 1。那么，无论如何操作，最大值至少还是 \(M\)，此时答案就是 \(M\)。
该算法的时间复杂度为 \(O(nm)\)，符合题目要求。
参考代码
#include <cstdio>
#include <vector>
using namespace std;
void solve() {
int n, m; scanf("%d%d", &n, &m);
vector<vector<int>> a(n + 1, vector<int>(m + 1));
int mx = 0;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
scanf("%d", &a[i][j]);
if (a[i][j] > mx) mx = a[i][j];
}
}
vector<int> cntx(n + 1), cnty(m + 1);
int cnt = 0;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (a[i][j] == mx) {
cntx[i]++; cnty[j]++;
cnt++;
}
}
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (cntx[i] + cnty[j] - (a[i][j] == mx) == cnt) {
printf("%d\n", mx - 1);
return;
}
}
}
printf("%d\n", mx);
}
int main()
{
int t; scanf("%d", &t);
for (int i = 1; i <= t; i++) {
solve();
}
return 0;
}
习题：CF463C Gargari and Bishops
解题思路
假设某个象在白格，按照题意可以发现，此时其他的白格也无法放另一个象。因此实际上这两个象放在两种不同颜色的格子上。要求得分最大，相当于求两种颜色的格子中可以沿两对角线方向可取到的总和最大。
因此可以预处理每条主对角线、反对角线上的总和，从而在两种颜色的格子中各自找总得分最大的结果。
参考代码
#include <cstdio>
#include <algorithm>
using namespace std;
using ll = long long;
const int N = 2005;
int a[N][N];
// d1为主对角线，d2为反对角线
ll d1[N * 2], d2[N * 2], ans[2];
int x[2], y[2];
int main()
{
int n; scanf("%d", &n);
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++) {
scanf("%d", &a[i][j]);
d1[i - j + n] += a[i][j];
d2[i + j] += a[i][j];
}
x[0] = 1; y[0] = 1; x[1] = 1, y[1] = 2;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++) {
int cur = (i + j) % 2;
ll sum = d1[i - j + n] + d2[i + j] - a[i][j];
if (sum > ans[cur]) {
ans[cur] = sum; x[cur] = i; y[cur] = j;
}
}
printf("%lld\n%d %d %d %d\n", ans[0] + ans[1], x[0], y[0], x[1], y[1]);
return 0;
}
习题：P5914 [POI 2004] MOS
解题思路
当剩 4 个人及以上时，考虑把最慢的两个人送过去。此时有两种策略：
- 最快的人来回接。
- 最快的人和第二快的人先过去，最快的人把火把带回来，最慢的两个人过去，第二快的人把火把带回来。
在这两种策略中，选更优的一种执行，重复这个过程直到剩 3 个人以内。
证明见 https://www.luogu.com.cn/article/j52fejnx
参考代码
#include <cstdio>
#include <algorithm>
using namespace std;
using ll = long long;
const int N = 1e5 + 5;
ll t[N]; // 存储旅行者过桥时间的数组
int main()
{
int n;
scanf("%d", &n);
// 读取n个旅行者的时间，题目保证已按升序排列
for (int i = 1; i <= n; i++) {
scanf("%lld", &t[i]);
}
ll ans = 0; // 记录总耗时
// 循环处理，当人数大于3时，每次处理最慢的两个人
while (n > 3) {
// 贪心选择：比较两种策略的成本，取其小者
ans += min(t[1] + 2 * t[2] + t[n], 2 * t[1] + t[n - 1] + t[n]);
// 已经成功将最慢的两个人送过桥，问题规模减2
n -= 2;
}
// 处理 n <= 3 的收尾情况
if (n <= 2) {
// 如果剩下1或2个人，最优解就是最慢的那个人过桥的时间
// n=1: t[1]; n=2: t[2]
ans += t[n];
} else { // n == 3
// 如果剩下3个人，最优解是 t[1],t[3]过 -> t[1]回 -> t[1],t[2]过
// 总成本为 t[3] + t[1] + t[2]
ans += t[1] + t[2] + t[n];
}
printf("%lld\n", ans);
return 0;
}
习题：P1809 过河问题
解题思路
同 P5914 [POI 2004] MOS，区别是本题不保证输入的时间有序，所以需要先排序。
参考代码
#include <cstdio>
#include <algorithm>
using namespace std;
using ll = long long;
const int N = 1e5 + 5;
ll t[N];
int main()
{
int n; scanf("%d", &n);
for (int i = 1; i <= n; i++) {
scanf("%lld", &t[i]);
}
sort(t + 1, t + n + 1);
ll ans = 0;
while (n > 3) {
ans += min(t[1] + 2 * t[2] + t[n], 2 * t[1] + t[n - 1] + t[n]);
n -= 2;
}
if (n <= 2) {
ans += t[n];
} else {
ans += t[1] + t[2] + t[n];
}
printf("%lld\n", ans);
return 0;
}
习题：ABC057D Maximum Average Sets
解题思路
如何求最大平均价值？
为了让平均值（总价值除以物品数量）最大，应该尽可能选择价值高的物品。
假设已经选择了 \(k\) 个价值最高的物品，它们的平均值是 \(avg_k\)。如果再选择第 \(k+1\) 高的物品，因为它的价值不会超过 \(avg_k\)（否则它就不是第 \(k+1\) 高的了），所以新的平均值 \(avg_{k+1}\) 必然小于或等于 \(avg_k\)。
这意味着，选择的物品越多，平均值要么越低，要么保持不变，不会变高。题目要求选择 \(A\) 到 \(B\) 个物品，因此，为了获得最大平均值，应该选择数量最少的情况，即选择 \(A\) 个价值最高的物品。
如何计算方案数？
定义一个“临界价值”，即选择的 \(A\) 个最大物品中，价值最小的那一个的价值。在升序排序的数组 \(v\) 中，这个值是 \(v_{n-A+1}\)。
根据这个“临界价值”与数组中最大价值 \(v_n\) 的关系，可以分为两种情况。
情况一：最大的 \(A\) 个物品的价值不完全相同（即 \(v_n \gt v_{n-A+1}\)）。此时，最大平均值只能通过选择恰好 \(A\) 个物品来实现。如果选择更多物品，必然会拉低平均值。为了凑成这 \(A\) 个物品，必须全部选择那些价值严格大于临界价值的物品，并且从所有价值等于临界价值的物品中，选择若干个，以凑足 \(A\) 个，这个方案数就是一个组合数。
情况二：最大的 \(A\) 个物品的价值完全相同（即 \(v_n = v_{n-A+1}\)）。这意味着价值最高的若干个物品（至少 \(A\) 个）价值都相等，最大平均值就等于这个价值。此时，只要选择的物品价值都等于这个最大值，平均值就一定是最大值。因此，可以从所有具有该最大价值的物品中，选择 \(k\) 个，只要 \(A \le k \le B\) 即可，方案数是一堆组合数的累加。
参考代码
#include <cstdio>
#include <algorithm>
using namespace std;
using ll = long long;
const int N = 55;
ll v[N], c[N][N]; // v: 存储物品价值, c: 存储组合数 C(n,k)
int main()
{
int n, a, b;
scanf("%d%d%d", &n, &a, &b); // n:物品总数, a:选择数量下限, b:选择数量上限
// border 是升序排序后，第A大物品的索引
// 它是构成最大平均值的物品中，价值最小的那个（临界物品）
int border = n - a + 1;
// 预处理组合数 C(i, j)，并同时读入数据
c[0][0] = 1;
for (int i = 1; i <= n; i++) {
scanf("%lld", &v[i]);
c[i][0] = c[i][i] = 1; // 组合数边界 C(i,0)=1, C(i,i)=1
for (int j = 1; j < i; j++) {
// 组合数公式 C(i,j) = C(i-1, j) + C(i-1, j-1)
c[i][j] = c[i - 1][j] + c[i - 1][j - 1];
}
}
// 将价值从小到大排序
sort(v + 1, v + n + 1);
ll sum = 0; // 用于计算最大的A个物品的总价值
int cnt = 0; // 用于统计整个数组中，价值等于临界值 v[border] 的物品总数
// 一次循环完成两件事：计算总和、统计临界值物品数量
for (int i = 1; i <= n; i++) {
// 如果索引大于等于 border，说明是最大的A个物品之一，计入总和
if (i >= border) {
sum += v[i];
}
// 统计与临界值相等的物品总数
if (v[i] == v[border]) {
cnt++;
}
}
// --- 第一部分：输出最大平均值 ---
printf("%.8f\n", 1.0 * sum / a);
// --- 第二部分：计算并输出方案数 ---
// 情况一：最大的A个物品价值不全相同（临界值 < 最大值）
if (v[border] < v[n]) {
// 此时必须恰好选择A个物品
// 方案是：选择所有价值 > v[border] 的物品，再从价值等于 v[border] 的物品中补足
// need 计算的是：在最大的A个物品中，有多少个物品的价值等于临界值
int need = 0;
for (int i = border; i <= n; i++) {
if (v[i] == v[border]) {
need++;
}
}
// 总方案数 = 从cnt个临界物品中，选出need个
printf("%lld\n", c[cnt][need]);
} else { // 情况二：最大的A个物品价值全部相同（临界值 == 最大值）
// 此时，只要选择的物品价值都是这个最大值，平均值就最大
// 可以从所有价值为最大值的物品（共cnt个）中，选择 k 个 (a <= k <= b)
ll ans = 0;
for (int i = a; i <= b && i <= cnt; i++) {
// 累加所有可能的选择方案 C(cnt, i)
ans += c[cnt][i];
}
printf("%lld\n", ans);
}
return 0;
}
浙公网安备 33010602011771号