阿里2014年9月笔试中的一个算法设计题--擦黑板剩余数字

5、在黑板上写下50个数字：1至50.在接下来的49轮操作中，每次做如下动作：选取两个黑板上的数字a和b，擦去，在黑板上写|b - a|。请问最后一次动作之后剩下数字可能是什么？为什么？

题目参见：擦黑板剩余数字

当时写这道题目的时候并没有明显的思路，后来感觉应该用归纳法进行分析，但还没有理出来一个思路，程序写出来测试了下，3000次测试结果，剩下的都是奇数。

即，可能生下从1-50范围内的任意奇数

代码如下：

            HashSet<int> hsr = new HashSet<int>();
            int[] result;
            int flag = 3000;
            int count = flag;
            string inStr;
            int inNum;
            Console.WriteLine("请输入试验次数：");
            inStr=Console.ReadLine();
            if (int.TryParse(inStr,out inNum))
            {
                flag= flag > inNum ? flag : inNum;
                count = flag;
                while (flag > 0)
                {
                    ArrayList hs = new ArrayList();
                    for (int i = 1; i <= 50; i++)
                    {
                        hs.Add(i);
                    }
                    int hsCount;
                    Random rand = new Random();
                    for (int j = 0; j < 49; j++)
                    {
                        int r1, r2, delta;
                        int e1, e2;

                        hsCount = hs.Count;
                        r1 = rand.Next(0, hsCount);
                        e1 = (int)hs[r1];
                        hs.RemoveAt(r1);
                        hsCount = hs.Count;
                        r2 = rand.Next(0, hsCount);
                        e2 = (int)hs[r2];
                        hs.RemoveAt(r2);
                        delta = Math.Abs(e2 - e1);
                        hs.Add(delta);
                    }
                    if (hs.Count > 0)
                    {
                        Console.Write("第{0:d3}次试验:", flag);
                        foreach (int e in hs)
                        {
                            Console.Write("{0:d2}", e);
                            if (!hsr.Contains(e))
                            {
                                hsr.Add(e);
                            }
                        }
                    }
                    flag -= 1;
                    Thread.Sleep(10);
                    Console.WriteLine();
                }
                result = (int[])hsr.ToArray();
                Array.Sort(result);
                Console.WriteLine("{0:d4}次试验结果：", count);
                for (int k = 0; k < result.Length; k++)
                {
                    if (!k.Equals(result.Length - 1))
                    {
                        Console.Write("{0:d2},", result[k]);
                    }
                    else
                    {
                        Console.Write("{0:d2}", result[k]);
                    }
                }
            }
            else
            {
                Console.WriteLine("请输入正确的整数!");
                Environment.Exit(0);
            }    

 

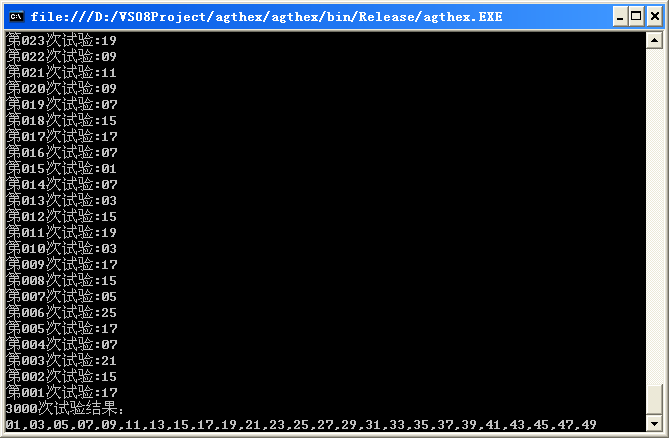
该为结果找个有说服力的理论~~~

update(@2013-11-1)偶尔看到恩格尔的《解决问题的策略》(参考链接)，刚翻几页就看到这个题目了，解释很简单，使用的是“不变量原理“。更一般的表述如下：

正整数n是奇数，在黑板上写下来1-2n，然后任意取两个数a，b，擦去这两个数并写上|a-b|，证明：最后留下的是一个奇数。

解：设S为黑板上所有数字的和，开始时S=n(2n+1)，是个奇数，每一步使S减少2min(a,b)，它是个偶数，所以S的奇偶性是个不变量，在整个简化过程中总有S≡1(mod 2)，所以最后结果是个奇数。