哈夫曼树（队列实现）

题意：

分析：
哈夫曼树
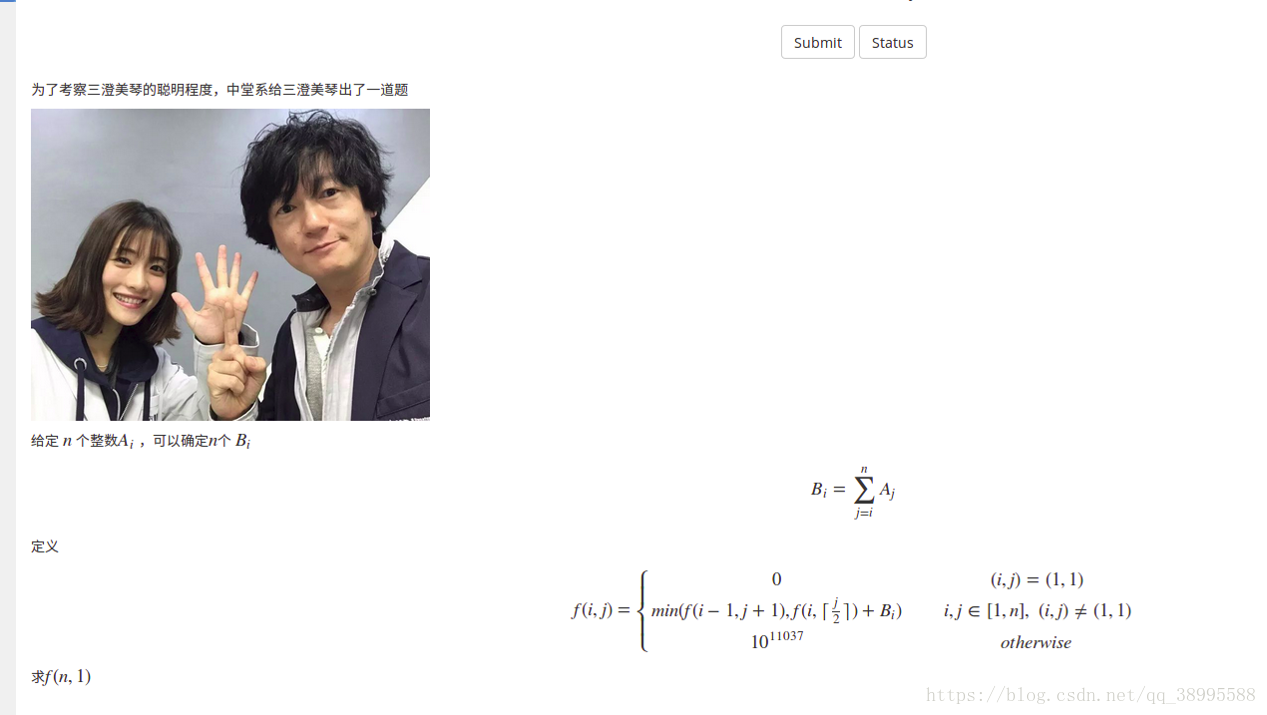
给定n个权值作为n个叶子结点，构造一棵二叉树，若带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树，权值较大的结点离根较近。

对于一颗哈夫曼树，我们把所有节点排序，权值大的必定层数较低，f[i][j]代表已经放了i-1个叶子节点，正准备放置Ai，该层还有j个空节点，我们可以选择在空节点上放一个叶子节点，从而转移到状态f[i+1][j-1]，或者选择移动到下一层，即转移到f[i][j*2]，该树权值增大量剩下节点的总权值。
各位有没有发现这个和该题的相似之处？我们可以发现上述过程正是把该题反过来进行的操作
因此f(n,1)就是该操作的最终结果——一棵最小权值树的各点权值和减去所有叶子节点权值和。

#include<cstdio>
#include<queue>
#include<vector>
#include<iostream>
#include<cmath>
#include<functional>
using namespace std;

int main() {
    int t;
    scanf("%d", &t);
    while (t--) {
        int n, tmp;
        long long ans = 0;
        priority_queue <int, vector<int>, greater<int> > q;
        scanf("%d", &n);
        while (n--) {
            scanf("%d", &tmp);
            q.push(tmp);
        }
        while (q.size() > 1) {
            int u = q.top();
            q.pop();
            u += q.top();
            q.pop();
            ans += u;
            q.push(u);
        }
        printf("%lld\n", ans);
    }
    return 0;
}