机器学习-习题（二）

目录


------ ### 2.1 数据集包含 1000 个样本, 其中 500 个正例、500 个反例, 将其划分为包含 70% 样本的训练集和 30% 样本的测试集用于留出法评估, 试估算共有多少种划分方式。 1. 共有1000个样本，训练集70%则有700个样本，测试集则有300个样本 2. 算一下训练集和测试集中分别包含多少个正例、多少个反例。设训练集包含正例$x$个，则测试集包含正例$500-x$，设训练集包含反例$y$个，则测试集包含反例$500-y$个样本，得出方程组： $$ \begin{cases} x+y=700 \ (训练集正反例样本共700个) \\ {x \over y}={{500-x} \over {500-y}} \ (分层采样，数据分布一致) \end{cases} $$ 　　易得$x=y=350$ 3. 划分方式共有$C_{500}^{350} \times C_{500}^{350}$ 或者 $C_{500}^{150} \times C_{500}^{150}$。两式在数学运算上相等，第一个表示从500个正例中随机取350个正例，依次取两次；第二个表示从500个反例中随机取150个反例，取两次。

2.2 数据集包含 100 个样本, 其中正、反例各一半, 假定学习算法所产生的模型是将新样本预测为训练样本数较多的类别 (训练样本数相同时进行随机猜测) , 试给出用 10 折交叉验证法和留一法分别对错误率进行评估所得的结果。

  1. 10折交叉验证法：
    （1）将100个样本等分为10个子集，每个子集包含10个样本。正反样本各占一半，即正反各5个。
    （2）任取其中9个子集作为训练集，剩余1个为测试集。
    （3）因为每个子集中两类样本数量相同，预测的结果均值近似于随机猜测。故其\(错误率=50 \%\)
  2. 留一法：
    将99个样本划分为训练集，剩下的1个样本为测试集。

\[若测试集为\begin{cases}反例，则训练集中包含50个正例、49个反例 \\正例，则训练集中包含50个反例、49个正例\end{cases} \]

根据题意（学习算法所产生的模型是将新样本预测为训练样本数较多的类别），分别产生正例模型、反例模型，同测试集全部相反。故其\(错误率=100\%\)

2.3 若学习器 A 的 F1 值比学习器 B 高, 试析 A 的 BEP 值是否也比 B 高。

\({1 \over F1}={1\over 2}\times({{1\over P}+{1\over R}})\)

\(BEP为P=R时，P或R的值\)

若\(F1_A>F1_B\)，则\(({{1\over P_A}+{1\over R_A}})<({{1\over P_B}+{1\over R_B}})\)

又因为\(BEP_A=P_A=R_A,BEP_B=P_B=R_B\)

若\(F1\)中\(P=R\)， 则\({{{2}\over{BEP_A}}<{{2}\over{BEP_B}}}\)，即\(BEP_A>BEP_B\)

但\(F1\)中\(P\)和\(R\)往往不一定相等（相等为特例），所以\(A\)和\(B\)的\(BEP\)值无法进行比较。当且仅当\(P=R\)时，\(F1\)与\(BEP\)存在关系。

2.4 试述真正例率 (TPR)、假正例率 (FPR) 与查准率 (P) 、查全率 (R) 之间的联系。

分类结果混淆矩阵如下。

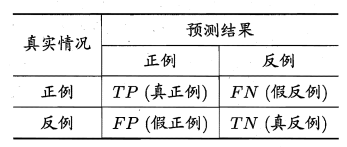
\[P={TP\over{TP+FP}}\\ R={TP\over{TP+FN}}\\ TPR={TP\over{TP+FN}}\\ FPR={FP\over{TN+FP}} \]

其中，\(R=TPR\)。而其他两个变量之间关系不明显。

2.5 试证明式 (2.22)。

\[AUC=\sum_{i=1}^{m-1}[{1\over 2}(x_{i+1}-x_i)\times(y_i+y_{i+1})] \tag{2.20} \]

\[l_{rank}={1\over m^+m^-}\sum_{{x^+}∈{D^+}}\sum_{{x^-}∈{D^-}}(Ⅱ(f(x^+)<f(x^-))+{1\over 2}Ⅱ(f(x^+)=f(x^-))) \tag{2.21} \]

\[AUC=1-l_{rank} \tag{2.22} \]

式2.20及2.21已经在机器学习-学习笔记（二）中证明。
\(AUC\)表示\(ROC\)曲线与\(x\)轴所围的面积，而\(l_{rank}\)表示\(ROC\)曲线与\(y\)轴所围的面积。\(ROC\)曲线\(x、y\)取值均为\([0,1]\)，故其总面积为\(1\)。所以\(AUC=1-l_{rank}\)。

2.6 试述错误率与 ROC 曲线的联系。

错误率：$$E(f;D)={{FP+FN}\over{TP+FN+FP+TN}}$$

\[TPR={TP\over{TP+FN}}\\ FPR={FP\over{TN+FP}}\]

通过公式不难看出，只要出现错误的样例，\(TPR\)值会减小，\(FPR\)值会增大，即按照\(ROC\)曲线绘制方法，出现假例时，会沿\(x\)轴移动，所以在\(ROC\)曲线在最接近于如下图红线时，错误率最低（基本接近于0）；当错误率等于\(50%\)时，即为随机胡猜，为图像中的蓝线。


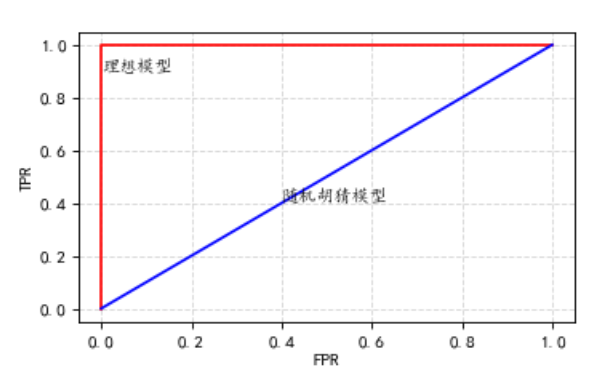
\(ROC\)曲线上每一个点都对应一个错误率，错误率越高，其\(ROC\)曲线越向\((1, 0)\)方向凹陷，若错误率越低，则\(ROC\)曲线越向\((0, 1)\)方向凸出。

2.7 试证明任意一条 ROC 曲线都有一条代价曲线与之对应, 反之亦然。

先证任意一条 ROC 曲线都有一条代价曲线与之对应。在代价曲线中，一条\(ROC\)上的一点代表代价平面上的一条线段，多个\(ROC\)的点组成了唯一的\(ROC\)曲线，同时，多个代价平面线段（如下图红色限度）共同构成了唯一的代价曲线（下图蓝色线段）。即证



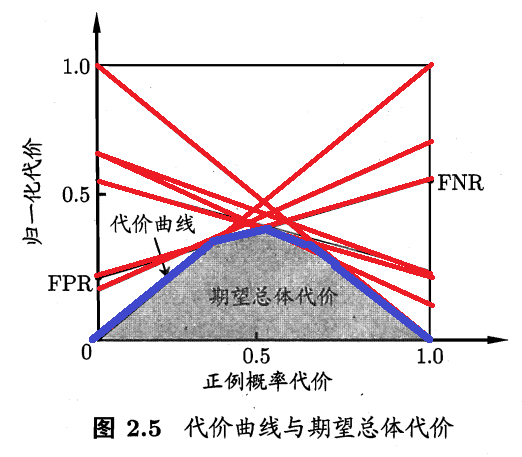
再证任意一条代价曲线都有一条 ROC 曲线与之对应。代价曲线上每一条线段都对应\(ROC\)曲线的一个点坐标，将代价曲线每一个线段都转化为\(ROC\)曲线上的点，将这些点按\(ROC\)曲线构造顺序连接，即可得出唯一的\(ROC\)曲线。但要注意的是，代价曲线反推得出的\(ROC\)曲线不一定是构造代价曲线的\(ROC\)曲线，可能比原来的少某几个点，例如，几条代价平面的线段交于同一点时，只可能选择其中两条，而多余的一条可能被忽略。但一定会有一条\(ROC\)曲线与其对应。

2.8 Min−max 规范化和 z−score 规范化是两种常用的规范化方法. 令 \(x\) 和 \(x′\) 分别表示变量在规范化前后的取值, 相应的, 令 \(x_{min}\) 和 \(x_{max}\) 表示规范化前的最小值和最大值, \(x′_{min}\) 和 \(x′_{max}\) 表示规范化后的最小值和最大值, \(\bar{x}\) 和 \(\sigma_x\) 分别表示规范化前的均值和标准差, 则 min−max 规范化、z−score 规范化分别如式 (2.43) 和 (2.44) 所示. 试析二者的优缺点。

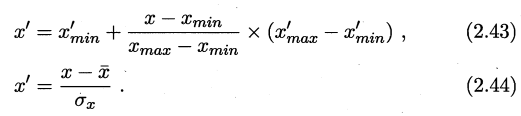
image

规范化：将原来的度量值转换为无量纲的值。通过将属性数据按比例缩放，通过一个函数将给定属性的整个值域映射到一个新的值域中，即每个旧的值都被一个新的值替代。
我所理解的规范化，其实就是将原有的数据等比例放大/缩小，使其映射到一个固定的数据范围中。
有3种规范化策略，分别是：最小－最大(min-max)规范化、z-score规范化、小数定标规范化。

Min-max规范化：

\[x^{\prime}=x_{\min }^{\prime}+\frac{x_{\max }^{\prime}-x_{\min }^{\prime}}{x_{\max }-x_{\min }} \times (x-x_{\min }) \]

\(\frac{x_{\max }^{\prime}-x_{\min }^{\prime}}{x_{\max }-x_{\min }}\)：等比例缩小
\(x-x_{\min }\)：原数据的偏移量
整个公式意思就是，将原数据的偏移量等比例缩小，再在新范围的最小值上加上缩小后的偏移量，即可得出新数据的值。
优点：很明显，Min-max规范化保留了原数据之间偏移量的关系；可以指定数据规范化后的取值范围；是计算复杂度最小的一个方法。
缺点：需要预先知道规范后的最大最小值；若原数据新增数据超越原始范围，则会发生“越界”错误；若原数据有值离群度很高（即使得原数据最大或最小值很大），规范后的大多数数据会特别集中且不易区分。

\(z-score\)规范化：

\[x^{\prime}=\frac{x-\bar{x}}{{\sigma}_{x}} \]

该公式表示原数据减去所有原数据的均值\(\bar{x}\)，再除以标准差\({\sigma}_{x}\)，即为规范化后的数据。

\[x_i^{\prime}=\frac{x_i-\bar{x}}{\sqrt{(x_1-\bar{x})^2+...+(x_i-\bar{x})^2+...+(x_n-\bar{x})^2}}\\ x_i^{\prime}=±\sqrt\frac{(x_i-\bar{x})^2}{{(x_1-\bar{x})^2+...+(x_i-\bar{x})^2+...+(x_n-\bar{x})^2}}\\ (若x_i>\bar{x},则取正值，否则取负值) \]

将公式变形后易知，\(z-score\)规范化，其实是在计算每个数据相较于均值的偏差距离平方所占的所有偏差距离平方和的比例。
优点：可以将不同标准的数据转化为同一标准下；规范化后的结果易于比较；对于离群度较高的数据敏感度低，不会太受影响。
缺点：每次新增或删除原数据，其均值\(\bar{x}\)和方差\(\sigma_{x}\)均可能改变，需要重新进行计算；根据其计算原理易知，规范化后的数据取值范围基本在\([-1,1]\)，数据之间分布较密集。

2.9 试述 \(χ^2\) 检验过程。

先引用浙江大学概率论与数理统计(第四版)第八章第三节对\(χ^2\)检验（卡方检验）的概念。


\(χ^2\) 检验（卡方检验）在浙大版概率论中已经阐明的面面俱到了，这里稍作总结一下。

\(χ^2\) 检验（卡方检验）：主要用于检验两个变量之间是否存在关系，检验局部数据是否符合总体数据分布。主要是比较实际值和理论值之间的偏离程度。
这里的\(χ^2\) 检验（卡方检验）对单个分布样本和多个分布样本均可检验，但其检验方法不同。

  1. 单个分布的\(χ^2\) 检验
  • 做出假设：\(H_0:总体X的分布函数为F(x)\)（这里的\(F(x)\)已知）
  • 将\(H_0\)下\(X\)所有可能取值分为互不相交的子集\(A_1,...,A_k\)
  • \(f_i\)记为样本观察值\(x_1,...,x_n\)落在\(A_i\)中的个数，则事件\(A_i\)发生的频率为\(\frac{f_i}{n}\)
  • \(p_i\)记为当\(H_0\)为真时，\(H_0\)所假设的\(X\)的分布函数计算\(A_i\)的概率。
  • 检验统计量

\[\chi^{2}=\sum_{i=1}^{k} \frac{n}{p_i}(\frac{f_i}{n}-p_i)^2=\sum_{i=1}^{k} \frac{f_i^2}{np_i}-n \]

  • 当\(\chi^2＜\chi_\alpha^2(k-1)\)，则接受\(H_0\)，否则拒绝。（当\(n≥50\)时，\(H_0\)为真时的\(\chi^2\)近似服从\(\chi^2(k-1)\)分布。）其中，\(\chi_\alpha^2(k-1)\)的值由\(\chi^2\)分布表给出。


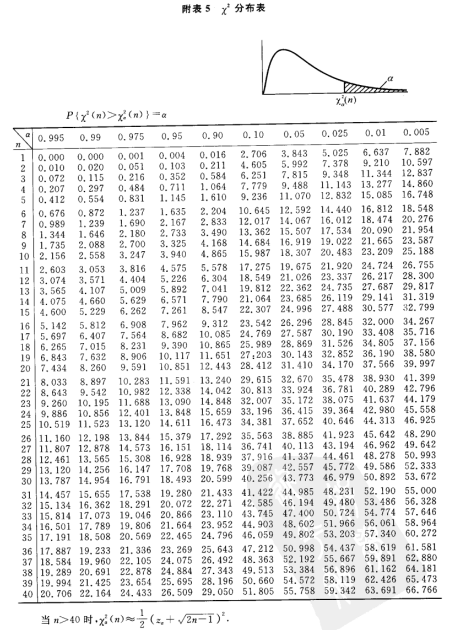
  1. 多个分布/分布族的\(\chi^2\)检验
  • 做出假设：\(H_0:总体X的分布函数为F(x;\theta_1,...,\theta_r)\)（这里的\(F(x)\)含有未知参数\(\theta_1,...,\theta_r\)，未知参数不同，则分布不同，所以\(F(x;\theta_1,...,\theta_r)\)代表分布族）
  • 定义检验统计量的方法同单个分布的基本相同，但是概率\(p_i\)因为参数未知，所以只能用估计值。这里先利用样本求出未知参数的最大似然估计，以估计值作为参数值，求出\(p_i\)的估计值\(\hat{p_i}\)

\[\chi^{2}=\sum_{i=1}^{k} \frac{f_i^2}{n\hat{p_i}}-n\sim\chi^2(k-r-1) \]

  • 其拒绝域同1相同\(\chi^2≥\chi_\alpha^2(k-r-1)\)

2.10 试述在 Friedman 检验中使用式 (2.34) 与 (2.35) 的区别。



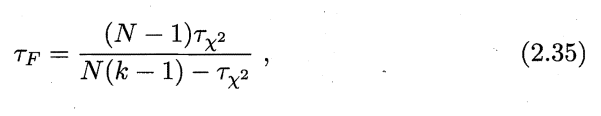
两式的区别在书中有所讲，2.34相较于2.35过于保守，2.34在\(k\)较小的情况下，倾向于认为无显著区别，而2.35恰恰可以解决这个问题。
这里要解决两个问题。第一个是为什么2.34保守，第二个是为什么2.35可以解决保守的问题。
第一个问题：为什么2.34保守？
其实不难理解，2.34服从自由度为\(k-1\)的\(\chi^2\)分布，其仅考虑了不同算法对方差产生的影响，而为考虑不同数据集对其产生的影响，所以较为保守。（这里应该通过对总体方差和样本方差的推导来证明）
第二个问题：为什么2.35可以解决保守的问题？
这里2.35就是服从自由度为\(k-1\)和\((k-1)(N-1)\)的F分布，既考虑了不同算法之间的影响，也考虑了不同数据集所带来的影响。（关于方差的推导过程，后续依次补齐）

posted @ 2022-06-07 20:40  RogZ  阅读(1635)  评论(0)  编辑  收藏  举报