hadoop datanode usages方差算法
stdDev 标准差(方差)
阐述及应用
简单来说,标准差是一组数值自平均值分散开来的程度的一种测量观念。一个较大的标准差,代表大部分的数值和其平均值之间差异较大;一个较小的标准差,代表这些数值较接近平均值。
例如,两组数的集合 {0, 5, 9, 14} 和 {5, 6, 8, 9} 其平均值都是 7 ,但第二个集合具有较小的标准差。
标准差可以当作不确定性的一种测量。例如在物理科学中,做重复性测量时,测量数值集合的标准差代表这些测量的精确度。当要决定测量值是否符合预测值,测量值的标准差占有决定性重要角色:如果测量平均值与预测值相差太远(同时与标准差数值做比较),则认为测量值与预测值互相矛盾。这很容易理解,因为如果测量值都落在一定数值范围之外,可以合理推论预测值是否正确。
标准差应用于投资上,可作为量度回报稳定性的指标。标准差数值越大,代表回报远离过去平均数值,回报较不稳定故风险越高。相反,标准差数值越小,代表回报较为稳定,风险亦较小。
此组数值的标准差为:
![STDDEV—标准差 \sigma = \sqrt{\frac{1}{N} \sum_{i=1}^N (X_i - \overline{x})^2}]()
-
简化计算公式
上述公式可以变换为一个较简单的公式:
 (皆为
(皆为
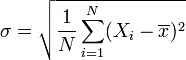



 浙公网安备 33010602011771号
浙公网安备 33010602011771号