线代总结5,6,7 特征向量，最小二乘，对称矩阵

1. 特征值与特征向量

矩阵作用于向量的特殊情况是它能等价于用一个常数作用于该向量。$A\mathbf{x}=\lambda\mathbf{x}$，其中$\lambda$称为特征向量，$\mathbf{x}$称为对应于$\lambda$的特征向量，$\mathbf{x}$是非0向量。

$\lambda$是A的特征值当且仅当$\left(A-\lambda\mathbf{I}\right)\mathbf{x=\mathbf{0}}$ 有非平凡解。

 

不同特征值对应的特征向量构成的集合线性无关。

 

 

 

 

 

 

 

对角化

$A=PDP^{-1}$   很多情况下A可以做这样的分解D是对角矩阵，这样可以方便求解A^{n} 。

考虑如果A有n个线性无关的特征向量。AP=PD ,其中P由这个n个向量组成，D是对应对角线上取相对应的特征值\lambda。

如果不是有n个不同的特征值，但是所有特征值对应的特征向量空间维数之和为n也可以。

 

 

 

 

2. 正交性与最小二乘法

正交投影， 最佳逼近定理

构造标准正交基的方法 格拉姆-施密特，对应 QR分解

 

最小二乘问题

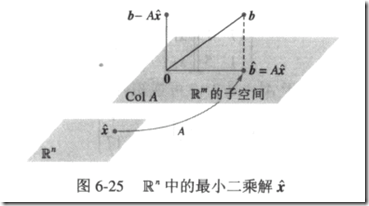
方程AX=b可能无解，我们可能希望求得一个最接近b的解。

||b-A\hat{x}||\leq||b-Ax||   \hat{x}对应最小二乘解，x是空间中任意向量。

这个解问题可以转化为求解将b投影到ColA空间的解，因为这个解对应与b的最近距离了。

image

\hat{b}=proj_{ColA}b    \[ A\hat{x}=\hat{b}\]

image

image

书中给出例子当A中的列不是线性无关的时候会有自由变量，所以最小二乘解不是唯一的，但是投影是唯一的。

 

 

 

 

 

 

 

 

 

3. 对称矩阵

书中介绍的思路总的来说是特殊化的，随着特殊化，比如到对称矩阵，它具有更多更好的特性。

前面提到的对角化P矩阵对应于对称矩阵，则同时是正交矩阵的，如果正交对角化一定是对称矩阵，

而且对称矩阵确保一定可以对角化。。

image

image

image

image

 

对称矩阵可以谱分解,逆对应转置

image

 

 

 

 

 

二次型

Q(X)=x^{T}Ax A是对称矩阵。

如果A是对角阵Q结果中不包含交叉项如x_{1}x_{2}, 利用前面对称矩阵对角化性质（考虑D可是对角阵)，我们可以通过坐标变换去掉交叉项。

 

image

 

 

 

二次型分类 ，正定，负定，不定  考虑上面主轴定理的坐标转换后，其实完全取决于特征值。

image

 

条件优化（限制x是单位向量情况下的二次型极值问题）

这里考虑的是对应一组单位向量中的变量使得二次型Q(x)最优化的问题。

结论是 对应取得最大最小值分别对应最大最小特征值，对应单位向量是对应特征值对应的特征向量。

 

 

LU分解（解方程，单位阵变换），QR分解（正交基，正交变换），奇异值分解（对角化）

posted @ 2011-02-20 19:02  阁子  阅读(1773)  评论(0)  编辑  收藏  举报