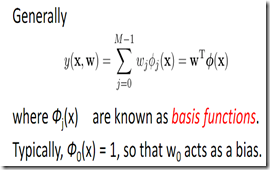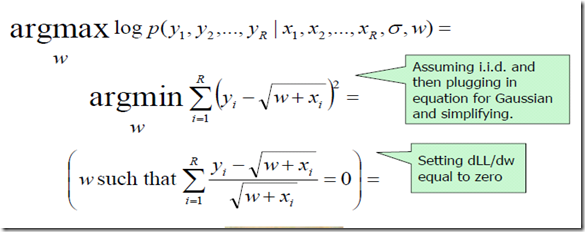预测实数取值的(real-valued)输出:回归入门
1. 简介:
主要是Andrew W.Moore 的课件Predicting real-valued outputs: an introduction to regression学习笔记(逐步完成)。
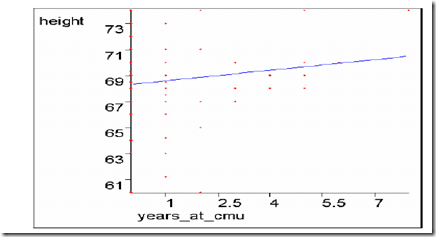
2. 单一参数线性回归 single parameter linear regression
前面关于PRML第一章学习笔记中已经贴了该部分。注意最后的最优求解很简单,按照偏导数=0。
对应最小值的
然后可以利用这个来预测新值。
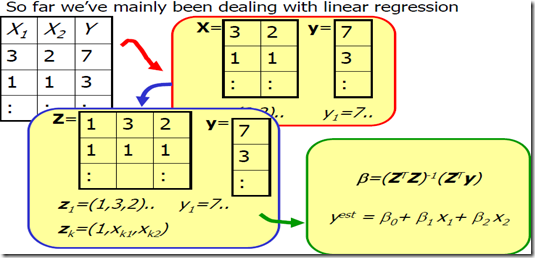
3. 多元线性回归
注意前面PRML中曲线拟合的例子,输入可不是多元的,仍然是f(X)->Y,X,Y都是单一变量而不是vector(不过参数W是多元的而已)。当然从basis function的角度来看其实也是一样的可以看做多元回归。
为什么取得最大可能对应的 是上面那个样子呢?其实这是一个最小二乘问题,也是线性方程组求解问题。设上图关于R个训练输入数据,每个数据有m个输入维度的矩阵是
=
如果
的解空间包含
,那么
方程是有解的。这个时候可以说对应的
使得对于训练数据的逼近最好,误差为0。那么如果解空间不存在
呢,那么我们只能尽可能的调整
使得
最小。我们求得的
是
中最接近
的向量。参考<<线性代数及其应用>>p359,
应该是
向
的列空间的投影。
正交投影 是唯一的,当
的列是线性无关的时候则有唯一的最小二乘解,即上面图中给出的。
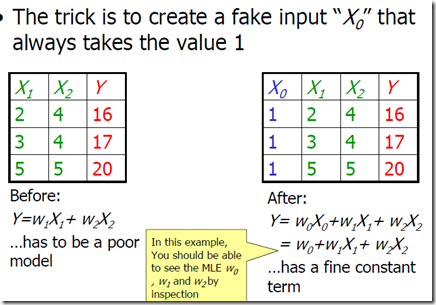
4. 线性回归中的常量
考虑一元线性回归,不穿过原点的情况,通常的做法是对数据的输入维度增加一个,其取值固定为1。
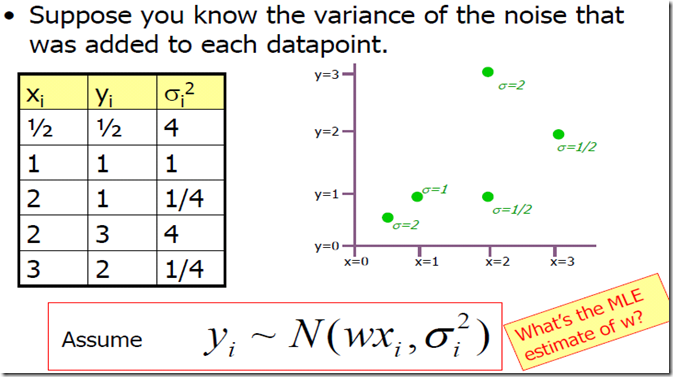
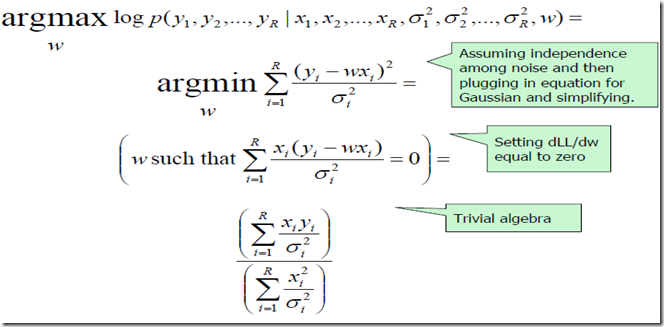
5. 异方差性:线性回归with varing noise
假设你知道加在每个数据点上的噪声的方差。如何利用MLE估计w?
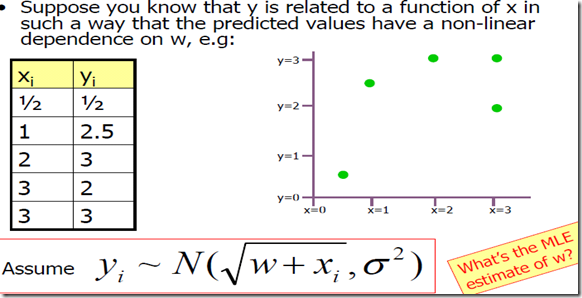
6. 非线性回归(Non-linear Regression)
假定你知道y和x的关系是一个有关w的非线性依赖关系。如何通过MLE估计W?
常用的一些方法
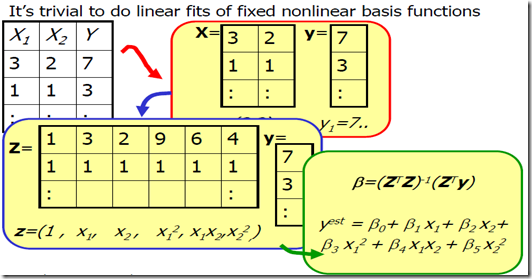
7. 多项式回归(Polynomial Regression)
下面第二个图给出了例子,即增加了类似的项,考虑PRML中给出的多项式曲线拟合,那个应该是属于一个1维input的M,order的情况。