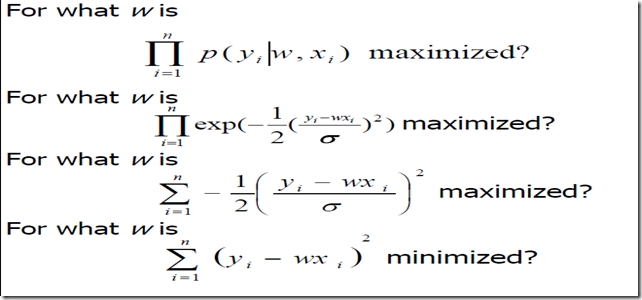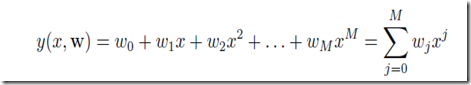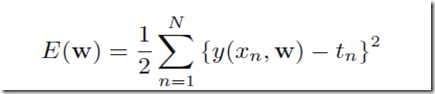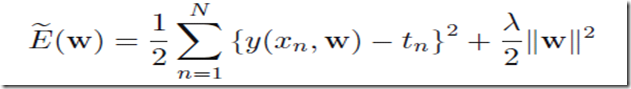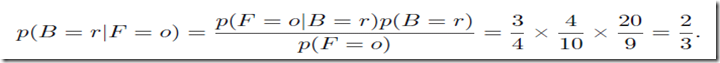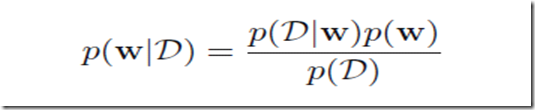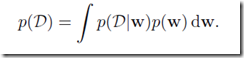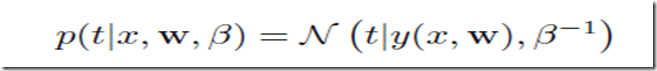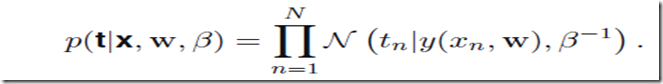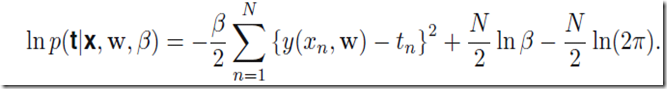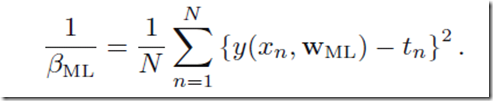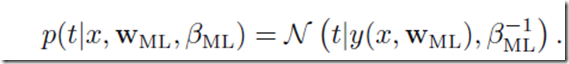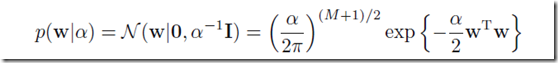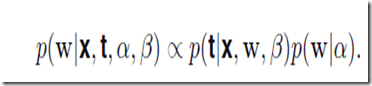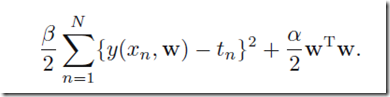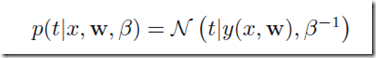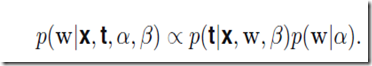PRML第一章学习总结最小二乘法数据拟合与回归

written by goldenlock

简介：

本文主要对PRML一书的第一章总结，结合moore关于回归的课件Predicting real-valued outputs: an introduction to regression。

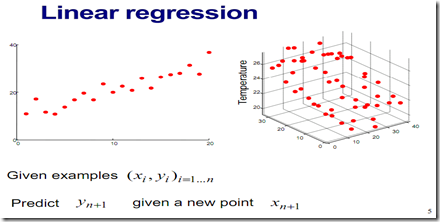
什么是回归(regression)?

1. 单一参数线性回归

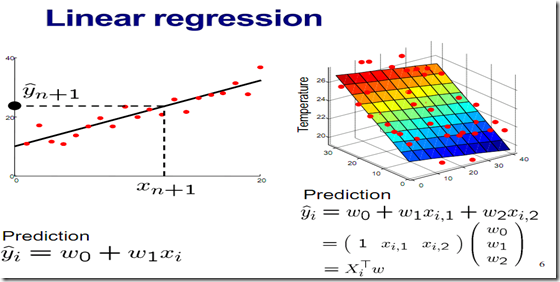
如上图考虑用一条过原点的直线去拟合采样点，y=wx,那么未知参数w取什么值可以使得拟合最好的，即整体拟合误差最小，这是一个最小二乘法拟合问题。

目标是使得(Xi-Yi)^2的总和最小。

2. 从概率的角度考虑上面的问题

就是说我们假定模型是y=wx但是具体的(Xi,Yi)对应生成的时候按照高斯分布概率模型，以WXi为中心,方差未知。具体每个采样点之间是独立的。

${)}10P~}A7EW$M7}[_E3$_P$

上面提到我们的目标是通过样本集合的实际观察值去预测参数W的值。怎样预测W的值呢，有两个思路即上面提到的

MLE 最大似然法即参数W取什么样的值能够使得我们已经观察到的实际样本集合出现的概率最大。ArgMax(P(Y1,Y2…Yn|X1,X2…Xn,W))，但是这样是不是有点奇怪，我们的目的其实是从观察的样本中估算最可能的W，ArgMax（W|x1,x2…xn,y1,y2…yn)

可以看到优化的目标其实和最小二乘法是一样的。

MAP 采用贝叶斯规则,后面再讲。

3.多项式曲线拟合

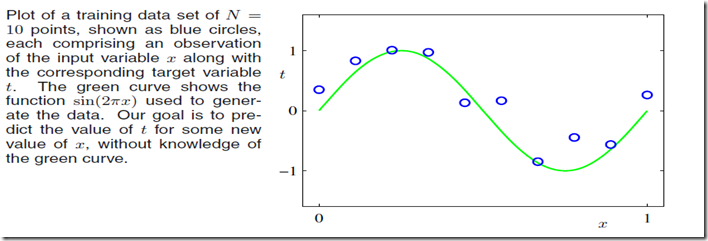
贯穿PRML第一章的例子是多项式曲线拟合的问题（polynomial curve fitting)。

考虑order为M的多项式曲线，可以表述为下面的形式:

曲线拟合的目标可以表述为优化是的下面的E(W)最小化(当然你可能会选取不同的error function这只是其中一种而已):

对于取到最小值的 $w$ 我们表示为 $w^{*}$ ，最优的最小距离是 $E(w^{*})$ 。

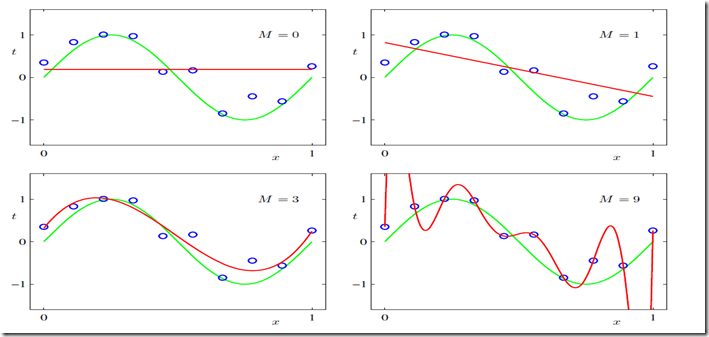
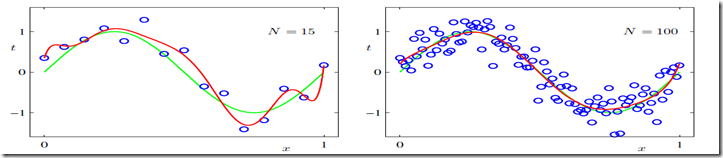
如果我们选择不同的order值即M不同的多项式曲线去拟合，比如取M=0，1，3，9最小二乘法拟合的结果如下图:

可以看到M=9的情况，曲线和采样观察点拟合的很好但是却偏离了整体，不能很好的反映 $sin(2\pi x)$ ,这就是传说中的over fitting过度拟合问题。

越高的order值M，对应越flexible的曲线，能够对采样点更好的逼近，毕竟高order的曲线包含了（可以表示）所有低order的曲线。另外 $sin(2\pi x)$

是包含所有order的，所以可以预见M越大对采样点拟合越好。但是从上图可以看出越大的M越flxible的曲线则对于噪声越敏感。

上面提到过度拟合问题，那么如何评判是否过度拟合呢？我们的终极目标是什么呢，终极目标是：

对于一个新的data,我们可以给出精确的值预测，即对于新的 $x_{new}$ 给出精确的估计 $y_{new}$ 。

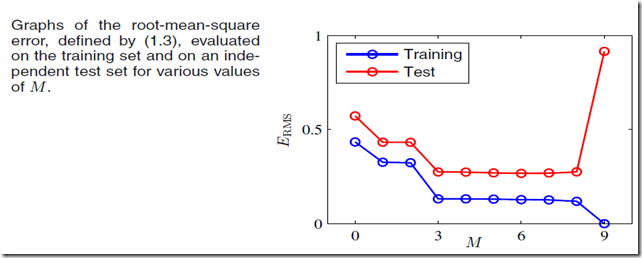
我们可以采用另外生成一个test数据集比如100个数据，对于每个M值，计算对于训练集trainning data的 $E(w^{*})$ 和对于测试集test data的 $E(w^{*})$ 。有的时候

可能用下面的误差函数更好:

$E_{RMS}=\sqrt{2E(w^{*})/N}$

这样可以使得对于不同的N即数据集合的大小有一个公平的比较基准。

对于过度拟合问题，如果增加观察点，则可以看到过度拟合的问题得以缓解,如下图M=9：

数据集合的大小越大，我们可以承受的模型复杂度越大。一个常见做法是数据(data points)应该多于参数数目的一定倍数（如，5，10）才能取得较好的效果。

在第3章中我们会看到，参数的数目并不是模型复杂度最好的度量。

同时很不爽的是我们需要根据训练集合的数据大小(size of the available training set)来限制模型的参数数目。看上去更自然的是根据要解决问题的复杂度来选择模型的复杂度。

我们将要看到最小二乘法和最大似然法是一致的（前面的单一参数线性回归的例子已经给了一个证明：）。如果采用贝叶斯方法，过度拟合问题可以避免。从贝叶斯的角度，实施用一个参数数目远多于data points的模型是可行的，事实上在贝叶斯模型，有效的参数数目可以根据data set的大小自动调整。

当下从最小二乘法的角度，为了解决过度拟合的问题，我们可以改变优化目标，加入reularization,限制|w|的值过大。

4. 贝叶斯概率

考虑仍一个硬币3次，假如我们3次观察到的结果都是背面，那么从最大似然的角度，我们会判定硬币观察到背面的可能性是100%，而如果我们有一定的先验知识我们不会得出这种结论。

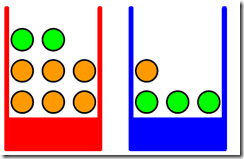
考虑我们有红色和蓝色两个盒子，红色的盒子里面有2个苹果6个橘子，蓝色的盒子有3个苹果1个橘子。

假定我们选取红色盒子的概率是40%，选取蓝色盒子的概率是60%，那么我们从2个盒子中取到一个苹果的概率是 (2/(2+6))*0.4 + (3/(3+1))*0.6=0.1+0.45=0.55=11/20，取到橘子的概率是0.45。

假定我们被告知我们取到了一个水果这个水果是橘子,那么我们是从哪个盒子里面取到它的呢？这个盒子是红色的可能性多大呢？显然直观的想试红色盒子的可能性不再是40%了（先验知识P(B=r)），而是变得更大了，因为红色的盒子里面更有可能取到橘子。即在知道取到是橘子的情况下盒子是红色的概率变大了（后验概率P(B=r|F=o),注意假如橘子在红色和蓝色中出现的可能性相同P(F=o)和P(F=o|B=r)相同则后验概率与先验概率相同,这个时候P(B=r)=P(B=r|F=o)即取到的水果和选取的盒子概率无关P(B=r,F=o)=P(F=o)*P(B=r|F=o)=P(F=o)*P(B=r) )。

贝叶斯理论用来帮助转换先验概率(prior probability)到后验概率(posterior probability)而转换的的依据是通过观察数据得到的信息。

对于曲线拟合中的参数w我们也可以利用贝叶斯理论，在观察训练数据前，我们有一个关于w的先验概率分布 $p(w)$ ,观察到的数据 $D={t_{1},t_{2}...t_{n}}$ , 可以表述为 $P(D|w)$ ,于是有

$P(D|w)$ 表示了在特定 $w$ 的情况下，观察到的数据发生的可能性。

5.概率角度重新看曲线拟合

曲线拟合问题其实是这样的，我们拥有的数据是N个输入数据X=（x1,x2,…xn),以及它们对应的目标值target value: t = (t1,t2,…tn),目标是对于给定的新的x我们给出目标值的预测t。(t取值是离散的话其实这就是分类问题），与开头的直线拟合一样，这里假设数据点符合独立的高斯分布，均值是y(x,w)即参数取w时候对应模型在取x时候的目标值，方差是 $\sigma^{2}=\beta^{-1}$ ,于是有