manachar算法求最大回文子串

manachar算法本质上是利用了回文串的对称特性, 在不断向右遍历的同时求一个对称点从而减少操作.

从这个入手 :

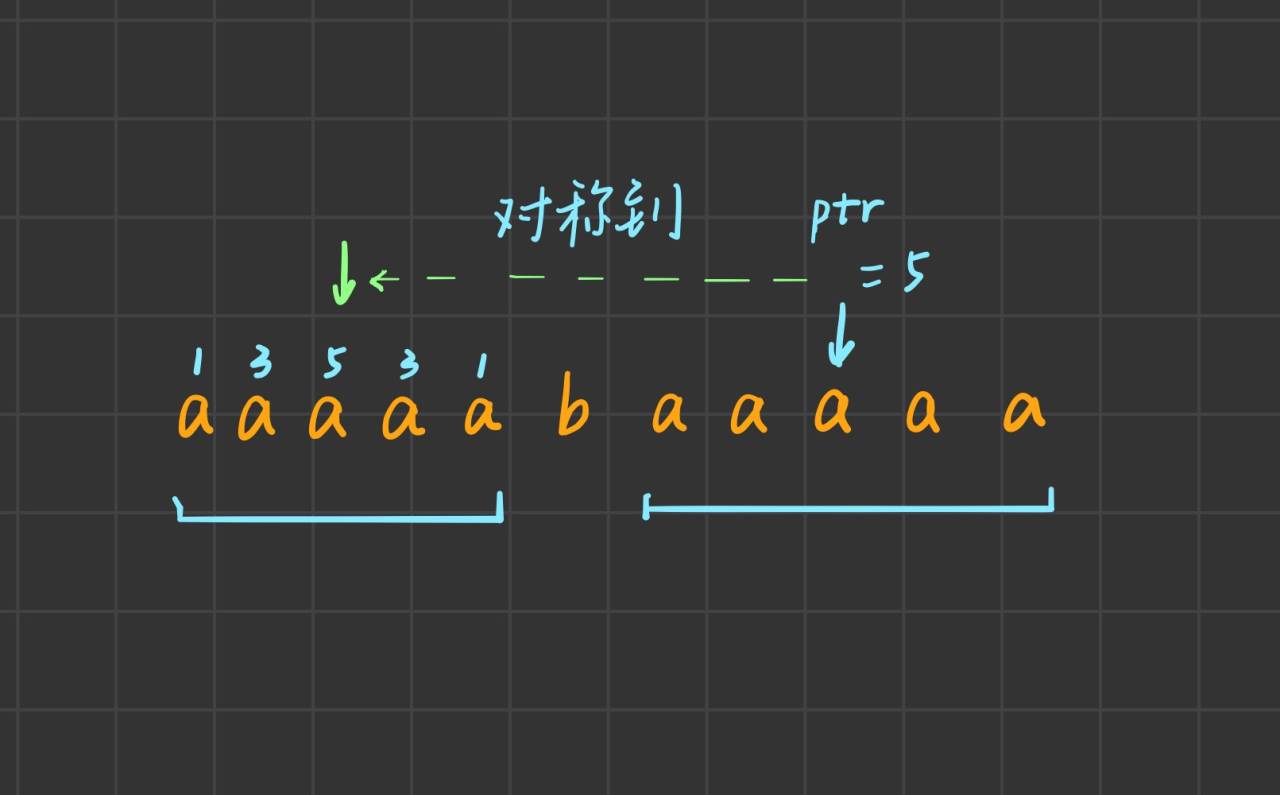
可以看到, 在遍历到ptr所指的位置时, 由于右边和左边完全对称, 我们可以直接求ptr关于b对称的对称点处的最大回文长度, 就是ptr处的回文长度.

关于manachar的具体介绍, 可以参考, 讲的都很详细:

1. 讲解1

2. 讲解2

这里只记录一下我写代码中碰到的几个问题和理解 :

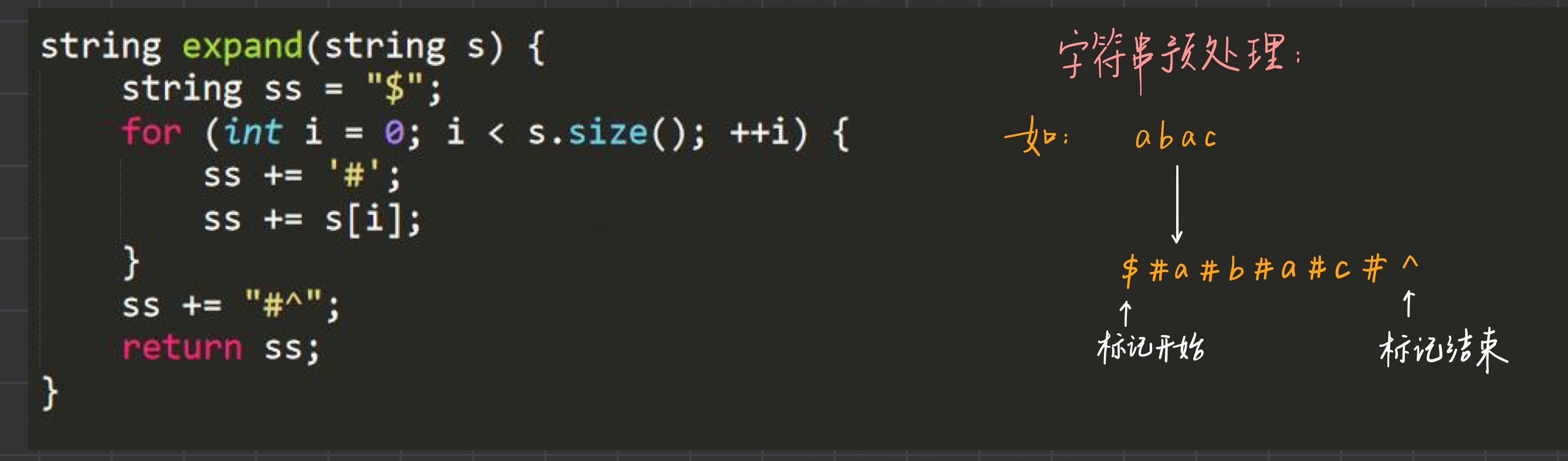
• 首先是字符串预处理, 由于存在aa和aba这两种形式的字符串, 为了统一操作, 我们在字符串中间加入分隔符# , 然后开始和结束的不同标记是为了在求回文时可以直接在边界结束而不发生越界 , 对应代码和解释如下 :

• 关于几个变量的设置

mx --- 所有回文串的最大右边界 (不包括在回文串中,及回文串的最后一位+1)
pos --- mx对应的回文串的中心点
lens[i] --- i为中心点包含'#'的的最大回文串长度的一半 ( 从i开始到回文串的右边界为止 )
lens[i]-1 --- i为中心点的最大回文串长度

lens的解释

• 程序的解释

• 关于时间复杂度的说明

由于manachar算法的核心就是扩展mx, 当mx到字符串末尾算法就结束了, 所以相当于mx从数组开始到结尾遍历了一遍, 时间复杂度就是\(O(n)\)

附一张关于mx更新的图解 :

ptr指向b时, 从b开始查找, mx更新到b对应的回文串边界处

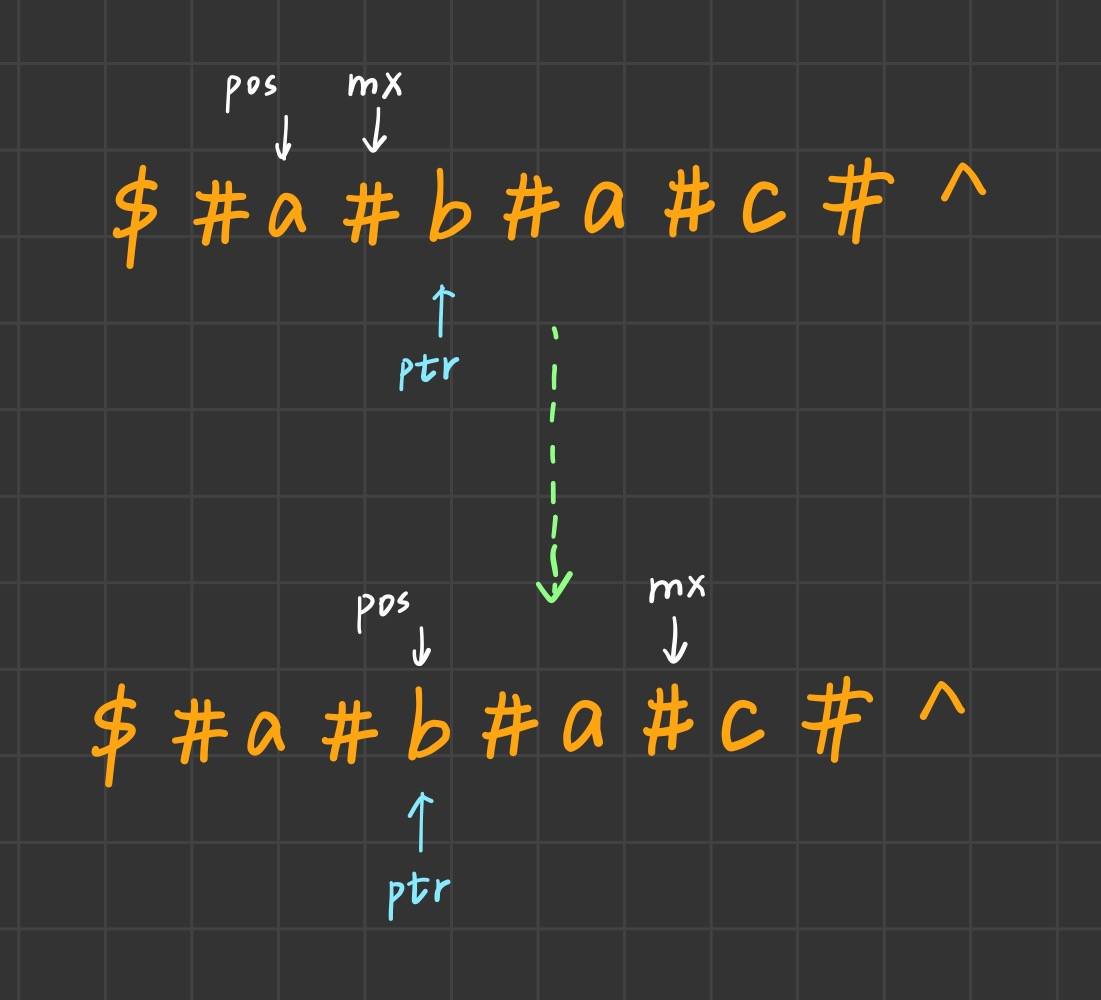
全部代码 :

const int maxn = 2000000 + 5;
int lens[maxn];

string expand(string s) {
	string ss = "$";
	for (int i = 0; i < s.size(); ++i) {
		ss += '#';
		ss += s[i];
	}
	ss += "#^";
	return ss;
}

int manachar(string s) {
	int mx = 0;
	int pos = 0;
	int ans = -1;
	for (int ptr = 1; ptr < s.size() - 1; ++ptr) {
		if (ptr < mx) 
			lens[ptr] = min (lens[2 * pos - ptr], mx - ptr);
		else
			lens[ptr] = 1;
		while (s[ptr - lens[ptr]] == s[ptr + lens[ptr]])
			lens[ptr]++;
		if (mx < ptr + lens[ptr]) { 
			mx = ptr + lens[ptr];
			pos = ptr;
		}
  		ans = max (ans, lens[ptr] - 1);
	}
	return ans;
}