[每日一题2020.06.15]P1226 【模板】快速幂取余运算

我是题目

快速幂就是快速求 \(a^b\)的一种算法

快速幂

思想 :

比如我要求 \(6^9\)

首先将幂转化为二进制形式 :

\[6^9 = 6^{1001} \tag{1} \]

可以得到 :

\[6^9 = 6^{2^{3}} \times 6^{2^0} \tag{2} \]

由于一个数变成二进制位数为\(\log _2\boldsymbol{b}\) 位, 故相对于直接求幂 ( b位需要b次计算 ), 时间复杂度减小了

取余

两条基本性质 :

\[\left( \boldsymbol{X}+\boldsymbol{Y} \right) \,\,\% \boldsymbol{a}\,\,=\,\,\left( \boldsymbol{X}\%\boldsymbol{a}+\boldsymbol{Y}\%\boldsymbol{a} \right) \%\boldsymbol{a} \tag{1} \]

\[\left( \boldsymbol{X}\times \boldsymbol{Y} \right) \,\,\% \boldsymbol{a}\,\,=\,\,\left( \left( \boldsymbol{X}\%\boldsymbol{a} \right) \times \left( \boldsymbol{Y}\%\boldsymbol{a} \right) \right) \%\boldsymbol{a} \tag{2} \]

上代码

ll qpow(ll x, ll y, ll mod)  { 
	ll ans = 1;
	ll base = x;
	while(y > 0) {
		if(y & 1){
			ans *= base;
			ans %= mod;
		}
		base *= base;
		base %= mod;
		y>>=1;
	}
	return ans % mod;
}

不取余的版本

ll qpow(ll x, ll y)  { 
	ll ans = 1;
	ll base = x;
	while(y > 0) {
		if(y & 1){
			ans *= base;
		}
		base *= base;
		y>>=1;
	}
	return ans;
}

与pow的时间比较

对比一下时间 :

快速幂 : 0.796s

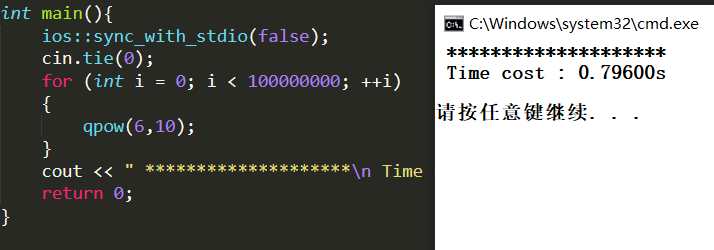
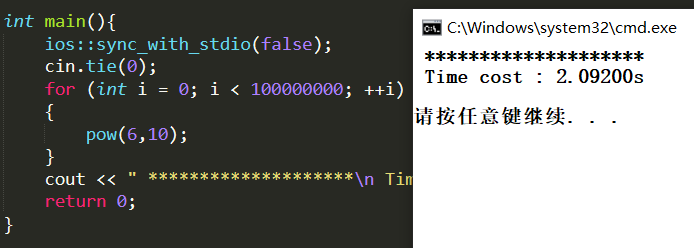
普通求幂 ：2.092s