图解KMP以及next数组的求法
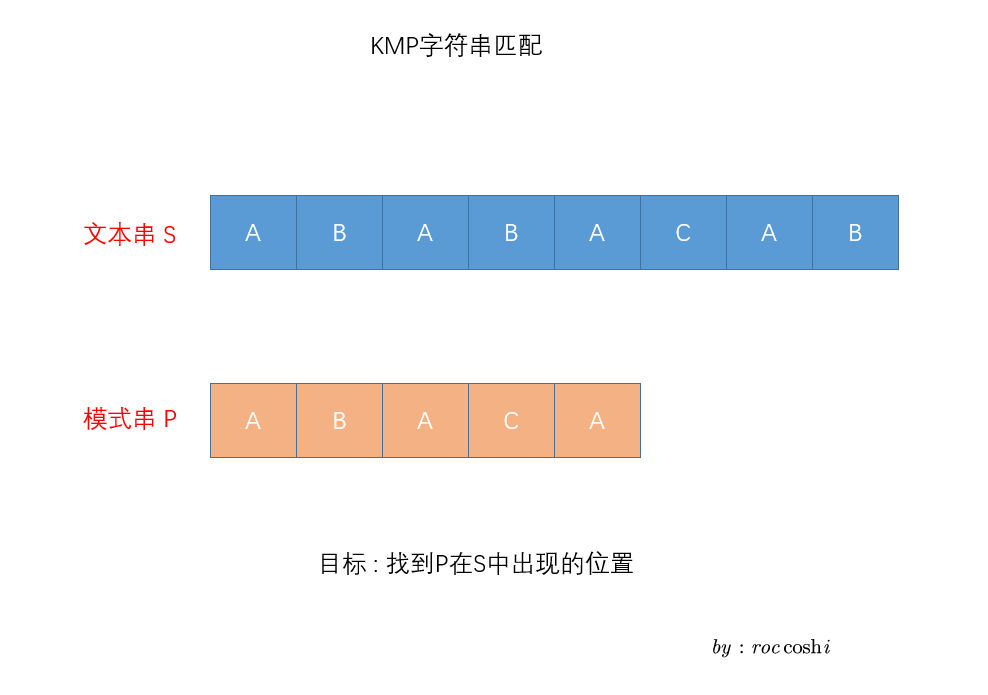
在计算机科学中,Knuth-Morris-Pratt字符串查找算法(简称为KMP算法)可在一个主文本字符串S内查找一个模式串P的出现位置。此算法通过运用对这个模式串在不匹配时本身就包含足够的信息来确定下一个匹配将在哪里开始的发现,从而避免重新检查先前匹配的字符。
今天写完kmp的题, 发现又想不通了, 这个next数组实在是太绕了, 去跑步的路上不禁一直在想, 终于恍然大悟了! 感觉十分有必要写一篇解释, 用自己的话说说kmp以及这个next. 一方面加深一下印象, 另一方面希望给偶然看到的人一点点启发 (
简介
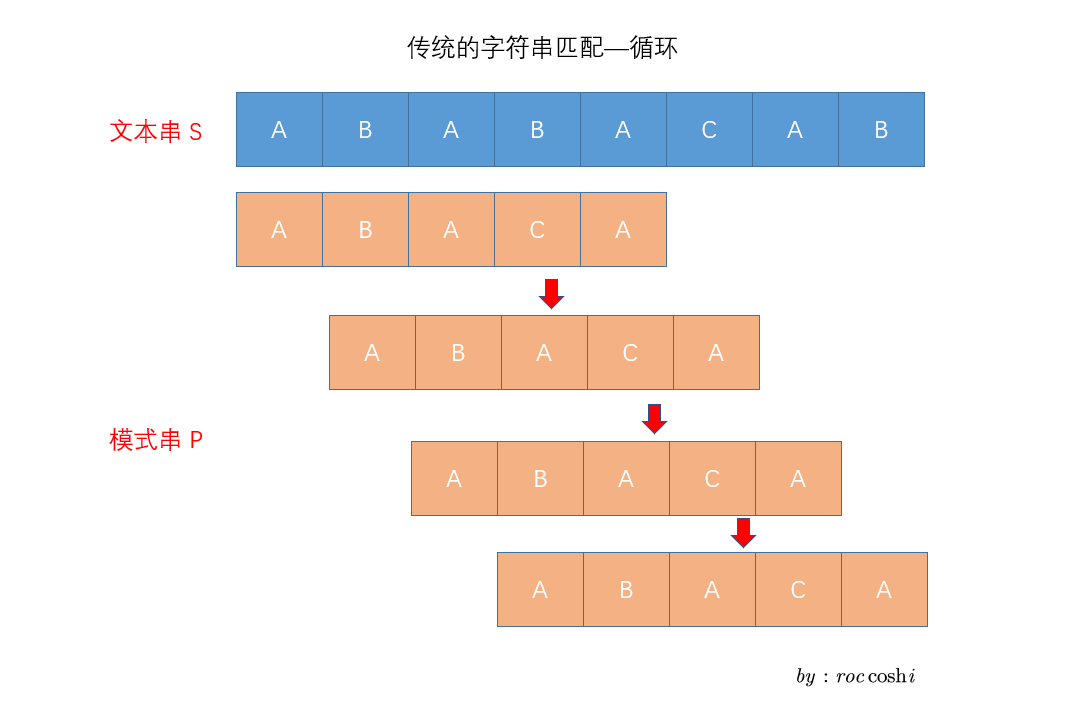
首先, 如果我们用传统的方式来匹配这个字符串, 会得到如下的过程:
如果用KMP算法, 将减少无用的挪动 :
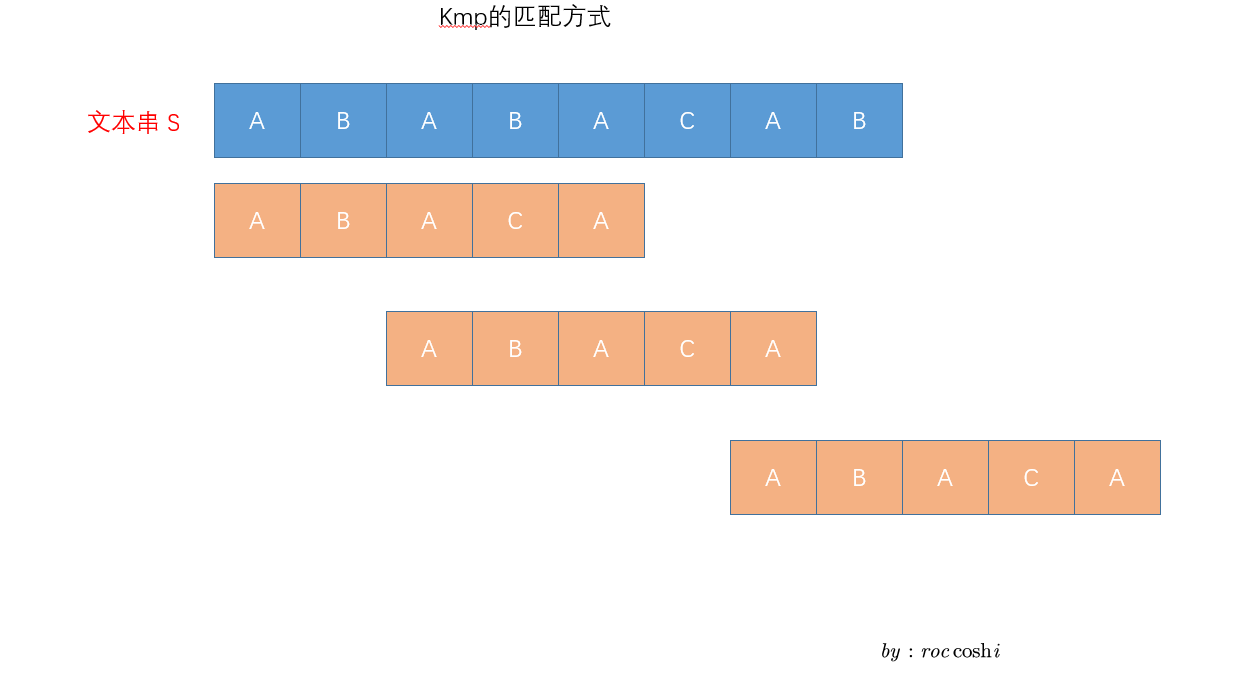
这么看可能还看不出什么, 如果我们稍微变化一下就可以看到KMP算法的巨大优势 :
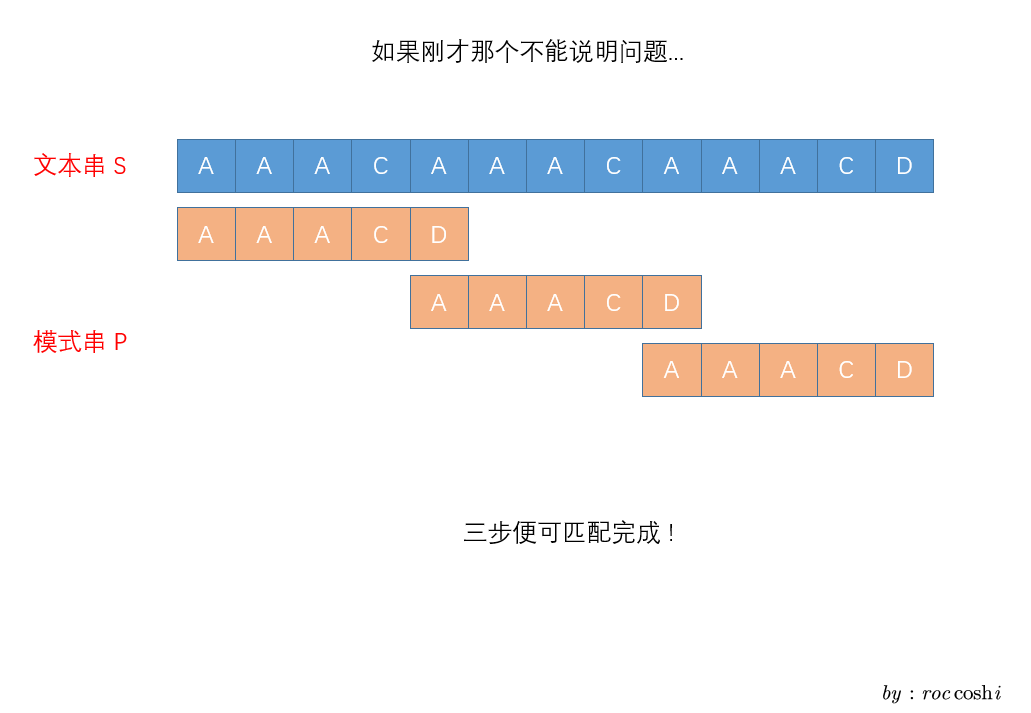
对于上图这种匹配, 普通的暴力算法将远远落后于kmp
kmp工作机制
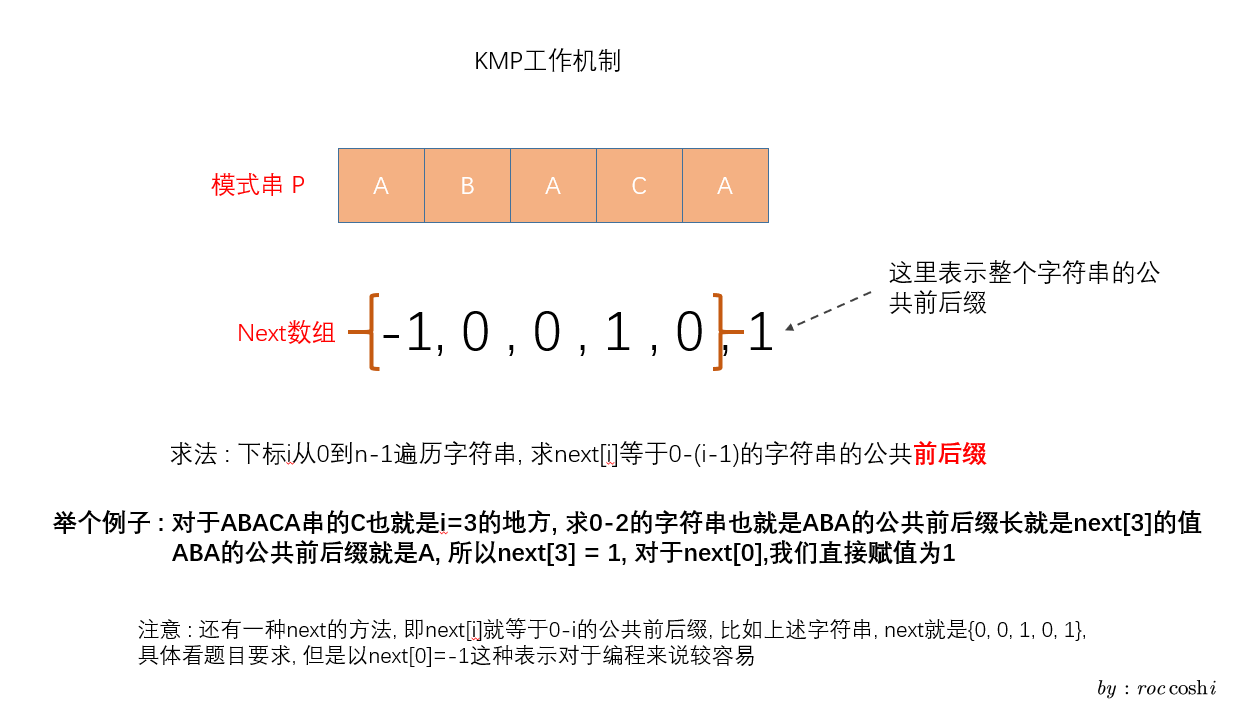
如果你不知道"前后缀" 也许以下的图能更好的帮助理解

上图来源于这里
匹配过程
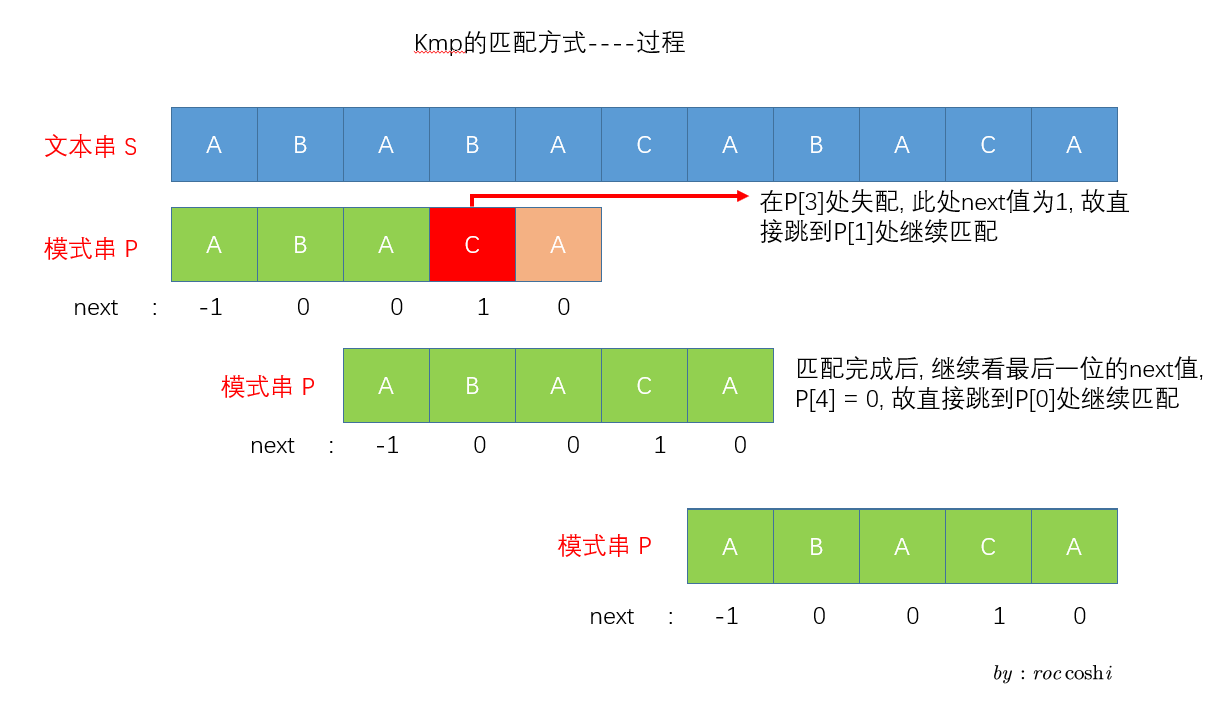
为什么是刚好跳转到next[i]
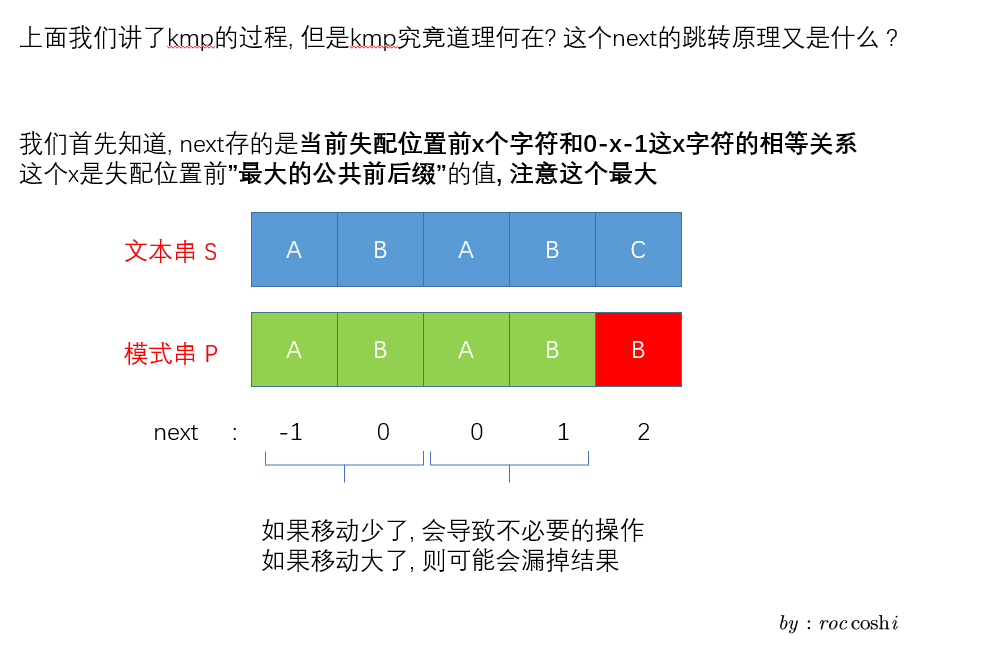
比如上面这个图中, 接下来我们会将失配位置移动到P[2]也就是A的地方(右移两下), 如果我们少移, 是不可能匹配的, 不然的话公共前后缀长度会比当前的值大
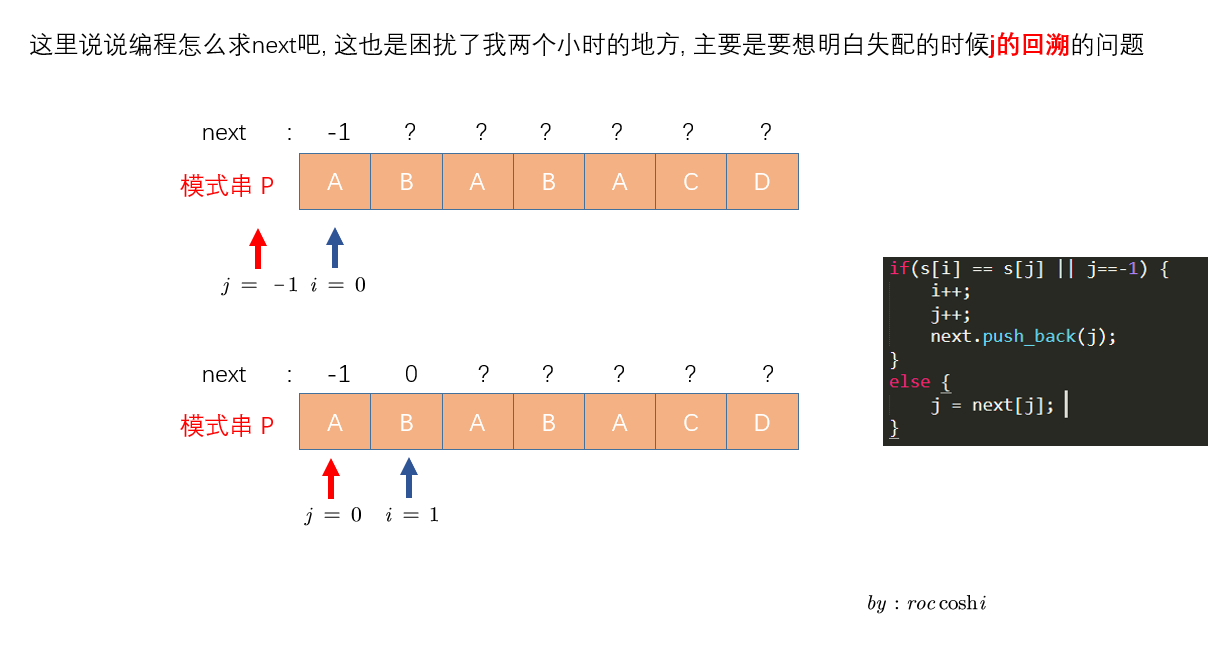
next数组的编程求法
重点 : 弄明白j回溯的原理
建议对照代码观看 :
int i = 0, j = -1;
while(i < s.size()) {
if(s[i] == s[j] || j==-1) {
i++;
j++;
next.push_back(j);
}
else {
j = next[j]; // 如果s[i]!=s[j]说明匹配失败, 回到上一级公共前后缀处
}
}
我们列出两个相邻的指针i和j, 初始指在数组前和0号元素的位置
接下来我列出从0开始求出next数组的图示
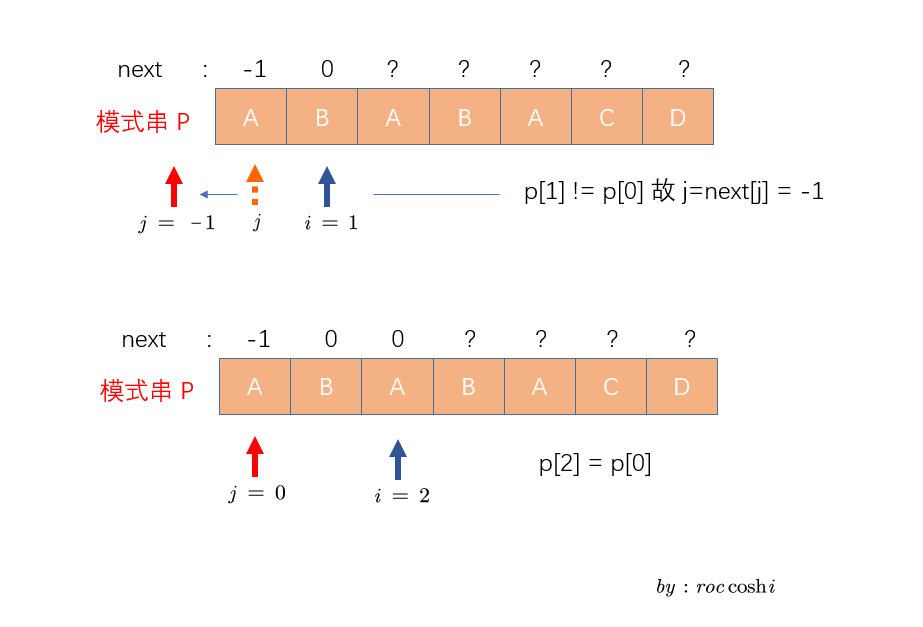
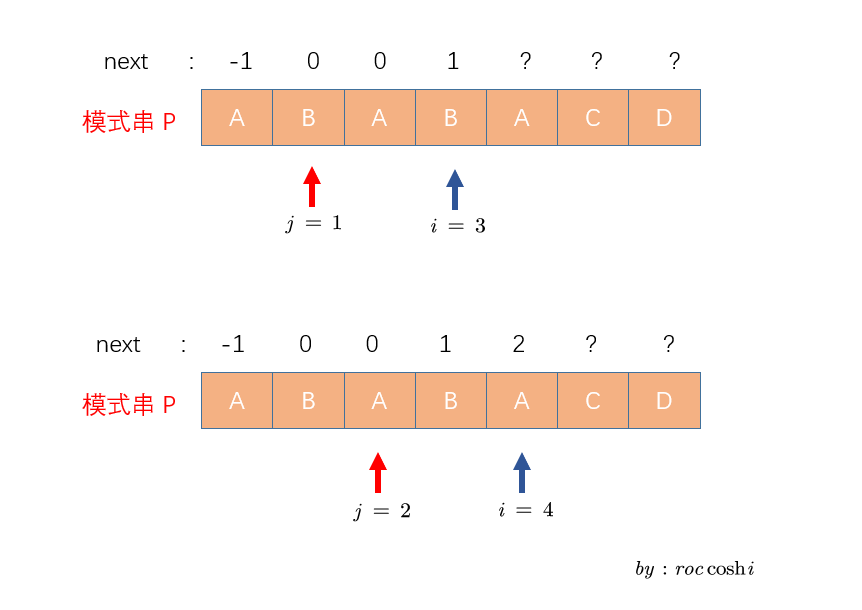
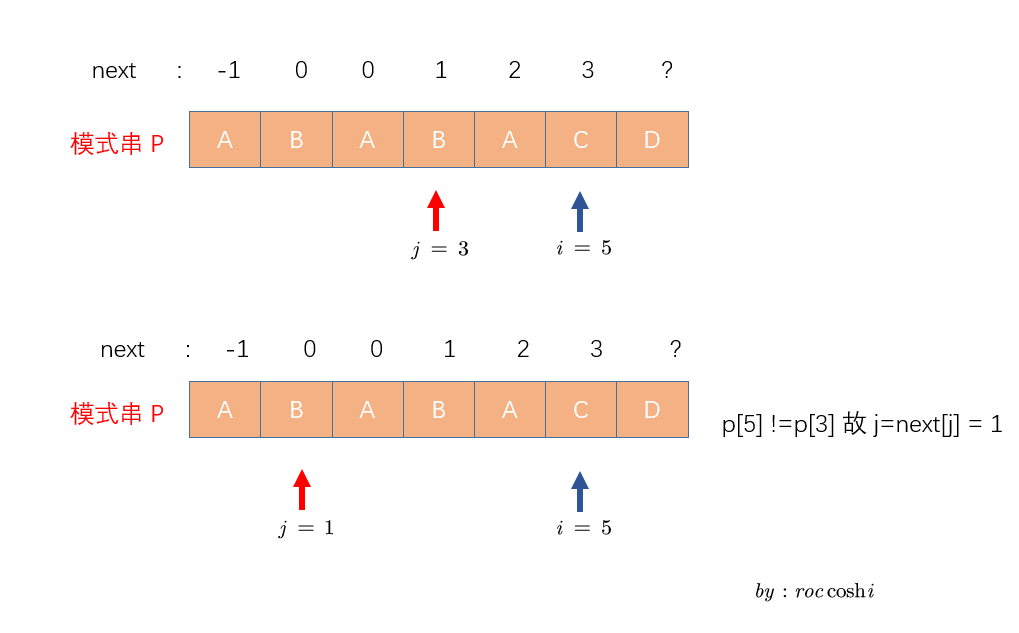
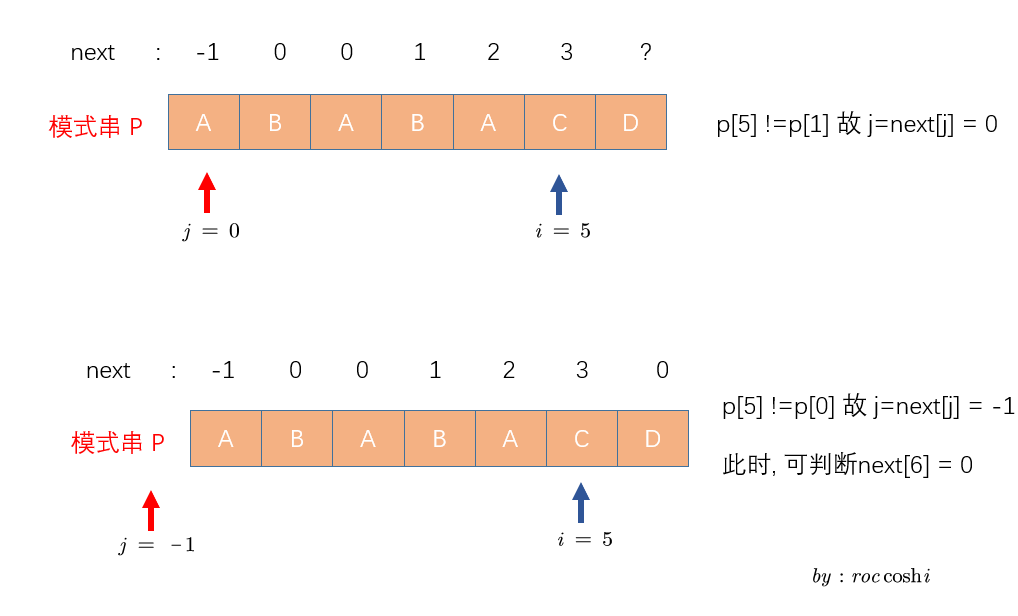
这里再附上两个写的不错的链接
http://www.ruanyifeng.com/blog/2013/05/Knuth–Morris–Pratt_algorithm.html
https://www.bilibili.com/video/BV1Px411z7Yo?t=1068
好累啊


 浙公网安备 33010602011771号
浙公网安备 33010602011771号