[每日一题2020.06.11]Codeforces Round #644 (Div. 3) H
A-E见 : 这里
我觉得很有必要把H拿出来单独发( 其实是今天懒得写题了 )
problem H
一个从 1 到 $ 2^m - 1$ 的长度为m的连续二进制序列, 删去指定的n个数, 问剩余的数的中位数是多少
看了题解还琢磨了一个小时才懂, 绝不能跟着题目傻傻的暴力来写
主要的思想还是动态调整的思想
首先比如我们制定m = 3
得到一串序列转换为十进制就是 0 1 2 3 4 5 6 7, 该怎么删才能在不用遍历的情况下找到中位数呢?
( 这题肯定不能暴力, 给定的m = 60, $ 2^{60} = 1152921504606846976 $ )
我们这里用一种动态维护的方式 :
比如n=3, m=3, 删去001, 011, 111
- 先不管三七二十一, 删去最末尾的那n个数, 判断假设这样删除的话最后的中位数是几
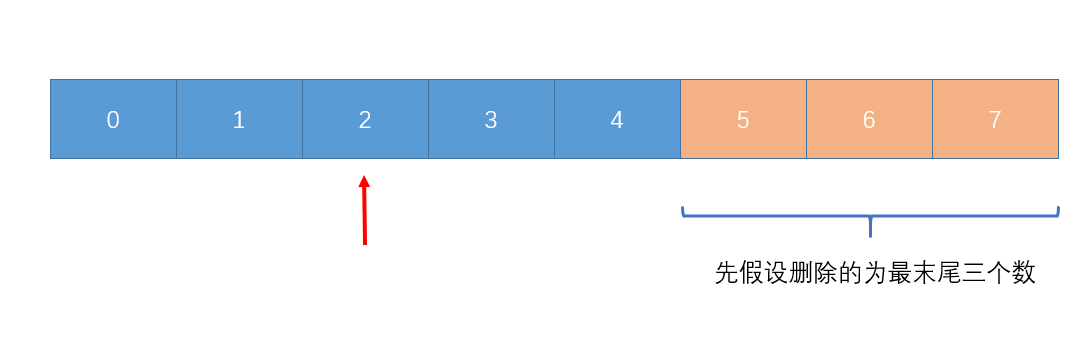
- 将删除队列从小到大排序, 依次维护调整 比如这里是1, 3, 7
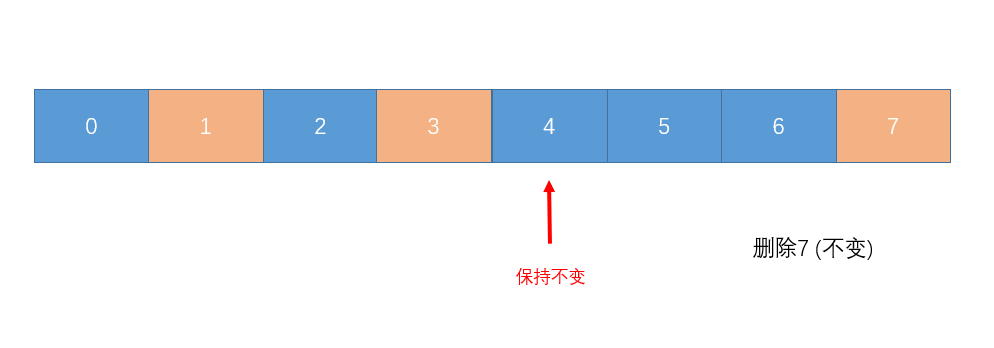
- 假如删除的为比目前所指向的值大的数, 则不用调整 why ? 见图 :
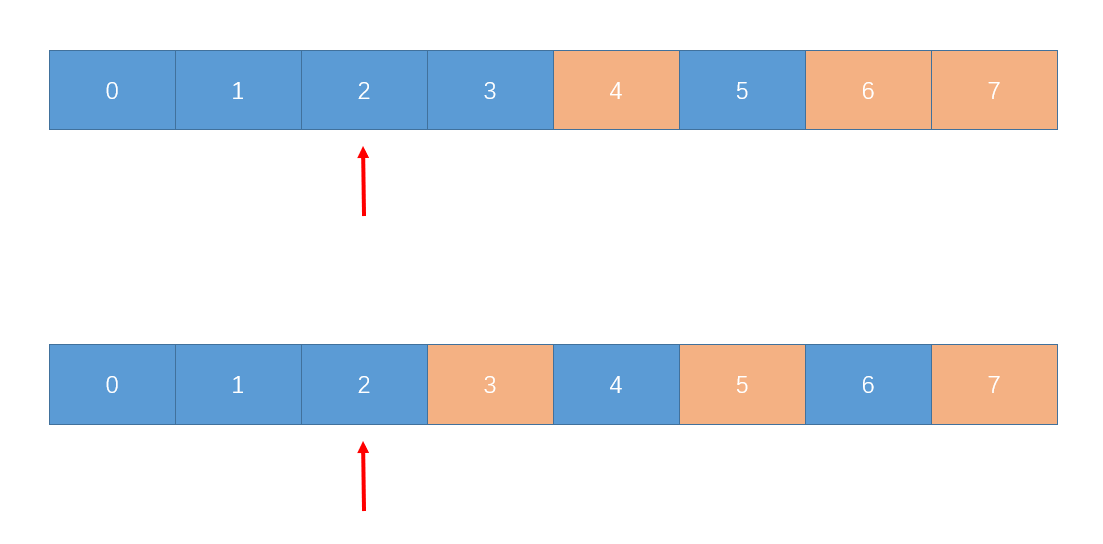
可以看到, 只要删除的数是比目前所指向的大的数, 中位数都是现在这个数, 不用变.
- 假如删除的为小于或等于目前所指向的值的数, 则指针++ why ? 见图 :
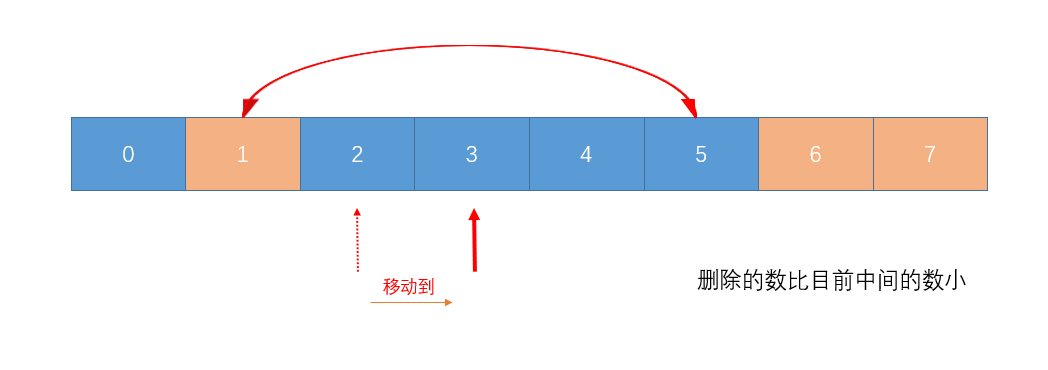
比如我们删除1, 那么相当于原本假设的删除的最后三个数少了一个, 前面增加了一个, 则删除后序列的中间值为现在的值+1 .
我们将3, 7继续删除 :
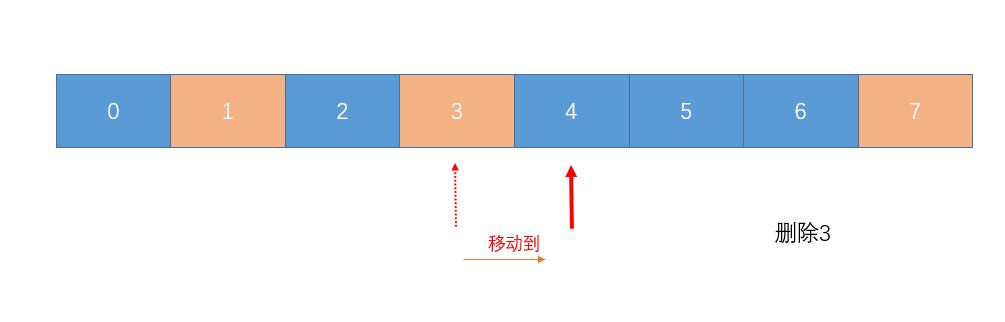
由于原本的值是从0连续的, 所以直接输出最后指针pos的值的二进制形式即为答案.
tips : 见到这种题, 一定要好好想想位置的计算, 很容易出现错误 !
pos的位置 :
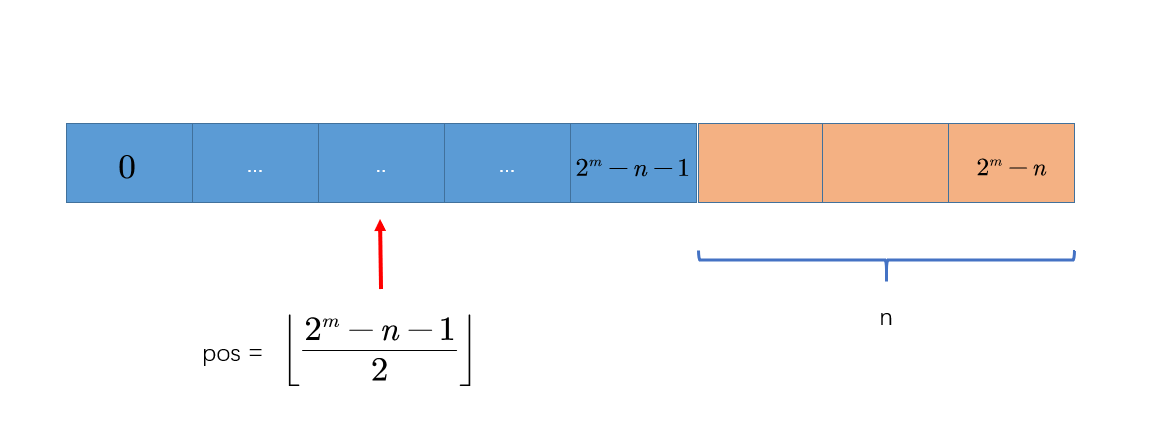
ac代码 :
/*
* Author: RoccoShi
* Time: 2020-06-10 20:05:02
*/
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll a[105];
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
int t;
cin >> t;
while(t--) {
int n, m;
cin >> n >> m;
for (int i = 0; i < n; ++i)
{
string s;
cin >> s;
ll tmp = 0;
for (int j = 0; j < m; ++j)
{
tmp = tmp*2 + s[j] - '0'; // 二进制 --> 十进制
}
a[i] = tmp;
}
sort(a, a + n);
ll pos = ((1ll<<m)-1-n) / 2;
for (int i = 0; i < n; ++i)
{
if(a[i] <= pos)
pos++;
}
string ans(m,'0');
for(int i = m-1; i >= 0; --i) { // 十进制 --> 二进制
ans[i] = (pos & 1) + '0';
pos >>= 1;
}
cout << ans << endl;
}
return 0;
}
这里注意下十进制二进制的相互转换代码 ( 建 议 背 诵 ) :
int x = 0;
for (int j = 0; j < m; ++j)
{
x = x*2 + s[j] - '0'; // 二进制s --> 十进制x
}
for(int i = m-1; i >= 0; --i)
{
ans[i] = (pos & 1) + '0'; // 十进制 --> 二进制
pos >>= 1;
}


