JPG学习笔记3(附完整代码)
采样后,需要对8*8block进行DCT(离散余弦变换)。为什么要进行DCT?第一点是余弦变化后的图片能量主要集中在低频,我们只需要保存低频数据,默认高频0。第二点是,DCT后的图片很适合哈夫曼压缩,对于原图而言,区域相连的pixle数值差不多,哈夫曼压缩效果差。全部代码在 https://github.com/Cheemion/JPEG_COMPRESS。
图片引用自"Compressed Image File Formats JPEG, PNG, GIF, XBM, BMP - John Miano"[1]
1.离散余弦变换直觉上的认识
假设我们有一个2*2的图片如下,最亮代表1, 最暗代表-1。

我们普通的认识是,这是一个由4个4维向量组成的一个图片(如下)。可以看成是一个2*2的平面向量,也可以看成4维向量(1,0,0,0)(0,1,0,0)(0,0,1,0)(0,0,0,1)。每个向量两两相交,并且都是单位向量。这4个基向量可以得到任何的一张2*2的图片。
(1,0,0,-1) = 1 *(1, 0, 0, 0) + 0 *(0,1, 0, 0) + 0 *(0, 0, 1, 0) + (-1) * (0, 0, 0, 1);
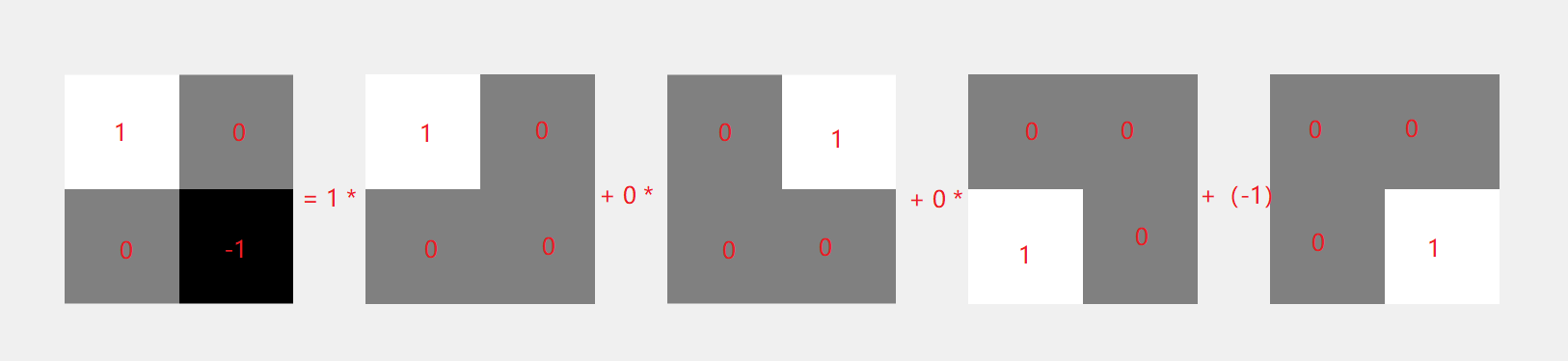
离散余弦变化,其实只是把上面的4个基向量进行了变化。如下
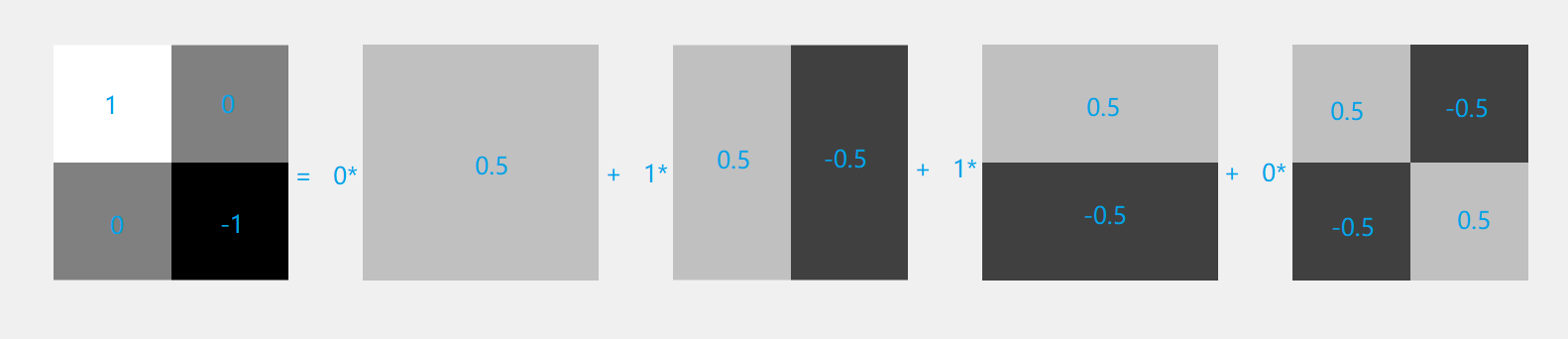
基向量变成了(0.5,0.5,0.5, 0.5)(0.5, -0.5, 0.5, -0.5) (0.5, 0.5, -0.5, -0.5) (0.5, -0,5, -0.5, 0.5),每个向量两两相交,并且都是单位向量。这4个基向量可以得到任何的一张2*2的图片。
所以DCT其实只是换了一个基向量而已。
下边左边第二个图为低频,因为整个图的颜色没有变化,可以认为变化频率为0
最右边的图为高频,上下和左右的颜色都变化了一次。
(1,0,0,-1) = 0 *(0.5, 0.5, 0.5, 0.5) + 1 *(0.5,-0.5, 0.5, -0.5) + 1 *(0.5, 0.5, -0.5, -0.5) + 0 * (0.5, -0.5, -0.5, 0.5);
蓝色的系数只要通过原图和新的基向量点乘就可以得到,比如向量(0.5, 0.5, 0.5, 0.5)前面的系数为 1 * 0.5 + 0 * 0.5 + 0 * 0.5 + (-1) * 0.5 = 0;
2.离散余弦变换公式上的认识
DCT离散余弦正变换
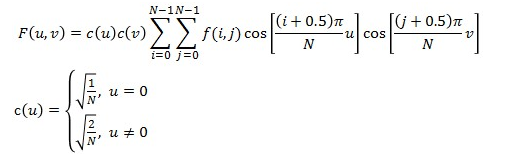
令G(i, j) = cos((i + 0.5) * pi * u /N) * cos((j + 0.5) * pi * u / N), u 和 v是constant
随着u和v从0到7(因为我们的block是8*8) 不断的变化我们可以画出如下图

画图代码matlab如下

function [ out ] = g( u,v )
p = zeros(8,8);
for i = 0:7
for j = 0:7
p(i + 1,j + 1) = cos((i + 0.5) * u * pi / 8) * cos((j + 0.5) * v * pi / 8);
end
end
out = p;
end

clc; clear; close all;
figure;
maximum = 0;
minimum = 100;
for u = 0:7
for v = 0:7
pp = g(u,v)
subplot(8, 8, u * 8 + v + 1);
imshow((pp + 1) ./ 2);
end
end
乘以系数c(u)c(v)是使我们的G(i, j)变成单位向量。公式剩余部分就是点乘的过程。
IDCT逆变换
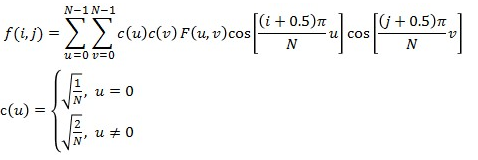
3.代码
void DCT(Block& block) { Block temp; std::memcpy(&temp, &block, sizeof(Block)); //copy from original //8 rows //DCT行变化 for(uint i = 0; i < 8; i++) { double* f = &temp[i * 8]; //one dimension Array , and will perform DCT on it for(uint k = 0; k < 8; k++) { double sum = 0.0; for(uint n = 0; n < 8; n++){ sum = sum + f[n] * std::cos(((n + 0.5) * M_PI * k / 8)); } sum = (k == 0) ? (sum * std::sqrt(1.0 / 8)) : (sum * std::sqrt(2.0 / 8)); block[i * 8 + k] = sum; } } std::memcpy(&temp, &block, sizeof(Block)); //copy from //DCT列变化 for(uint i = 0; i < 8; i++) { double* f = &temp[i]; //one dimension Array with 8 steps increment , and will perform DCT on it for(uint k = 0; k < 8; k++) { double sum = 0.0; for(uint n = 0; n < 8; n++){ sum = sum + f[n * 8] * std::cos(((n + 0.5) * M_PI * k / 8)); } sum = (k == 0) ? (sum * std::sqrt(1.0 / 8)) : (sum * std::sqrt(2.0 / 8)); block[i + k * 8] = sum; } } }
以上全部的代码在https://github.com/Cheemion/JPEG_COMPRESS/tree/main/Day3
完结
Thanks for reading.
wish you have a good day.
>>>> JPG学习笔记4





