【密码学】公钥密码体制概述

大体组成

与传统密码体制加密和解密使用相同密钥不同，公钥密码体制有两个密钥：

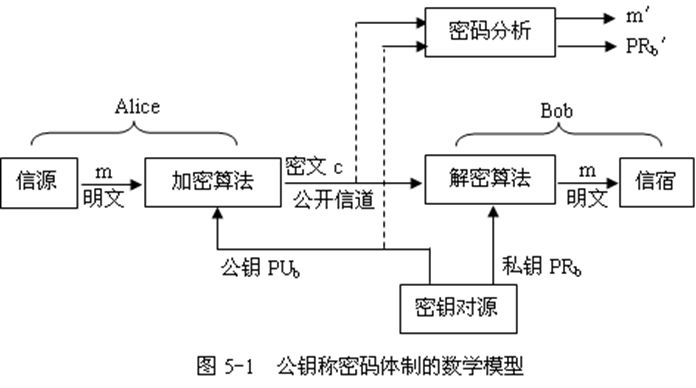
公钥密码体制的数学模型如5-1所示
情景：Alice要发送信息m给Bob
　　1. Alice用Bob的公钥PU（b）加密m并发送
　　2. Bob接受加密后的信息，用只有自己知道的私钥PR（b）进行解密，得到m
由于算法的严谨性，任何不知道Bob的私钥的人，都无法对加密的信息进行解密，也无法从公钥PU（b）推导出私钥PR（b）。

主要用途（局限性）
由于速度比对称密码算法要慢几个数量级，因此公钥密码算法至今主要用于数据安全，或用于短数据和密钥的加密。

实用的公钥密码体制应该满足以下的要求：
(1) 参与方B容易通过计算产生一对密钥 公开密钥PU（b）和私有密钥PR（b）。
（2）发送方A容易通过计算产生密文：c＝ePUb（m）
（3）接收方B容易通过计算解密密文：m＝dPRb（c）＝dPRb(ePUb(m))
（4）他人即使知道公开密钥PUb，要确定私有密钥PRb在计算上是不可行的。
（5）他人即使知道公开密钥PUb和密文c，要想恢复报文m在计算上也是不可行的。
（6）加密和解密函数可以以两个次序中的任何一个来使用:
m＝dPRb(ePUb(m)) m=ePUb(dPRb(m))

本质上是设计一种陷门单向函数。
陷门单向函数是密码学的核心。

陷门单向函数的定义：
• 正向计算容易。即如果知道x，计算y=f(x)相对容易。
• 反向计算极其困难。即如果知道y =f(x), 反向计算x=f^(−1) (y)非常困难
• 存在陷门δ，已知δ 时,对给定的任何y，若相应的x存在，则计算x使y=f(x)是容易的

至少三种攻击方式进行破解：
• 强力攻击(对密钥)
密钥穷举法搜索可能的私钥。
解决方法：密钥长度要足够长（但同时也增加了解密加密的速度）
• 公开密钥算法本身可能被攻破
从数学上对陷门单向函数寻求突破，从公钥PU推导出私钥PR。
目前没有严格证明该方法无效
• 可能报文攻击(对报文本身的强力攻击)
因为知道公钥PU，攻击者完全可以穷举所有可能的明文，用公钥来逐一加密这些明文，必有一个加密加过与截获的密文相同。
解决方法：明文也要足够长