算法学习——线性最小二乘法、拉格朗日乘子法
1）最小二乘法——求方差的平方和为极小值时的参数。
要尽全力让这条直线最接近这些点，那么问题来了，怎么才叫做最接近呢？直觉告诉我们，这条直线在所有数据点中间穿过，让这些点到这条直线的误差之和越小越好。这里我们用方差来算更客观。也就是说，把每个点到直线的误差平方加起来；接下来的问题就是，如何让这个S变得最小。这里有一个概念，就是求偏导数，通过偏导求极小值（方差）。比如导数就是求变化率，而偏导数则是当变量超过一个的时候，对其中一个变量求变化率。，我们都是在做不到完美的情况下，求那个最接近完美的解。
2）朗格朗日乘子法——求带有拉格朗日算子的目标复合函数极小值时的参数
举个例子：某工厂在生产过程中用到两类原材料，其中一种单价为2万/公斤，另一种为3万/公斤，而工厂每个月预算刚好是6万。就像下面的公式：
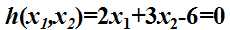
经过分析，工厂的产量f跟两种原材料（x1，x2）具有如下关系（我们暂且不管它是如何来的，而且假定产品可以按任意比例生产）
请问该工厂每个月最少能生产多少？
回到工厂的例子，其实就是求函数f的极值。上面我们提到，极值点可以通过求偏导（变化率为0的地方为极值点）来实现，函数f（x1，x2）对x1，x2分别求偏导，那么得出的结论是：x1，x2都为0的时候最小，单独看这个函数，这个结论对的，很显然这个函数的最小值是0（任何数的平方都是大于或等于0），而且只有x1和x2同时为0的时候，取得最小值。但问题是它不满足上面的限制条件。
怎么办呢？拉格朗日想到了一个很妙的办法，既然h（x1，x2）为0，那函数f（x1，x2）是否可以加上这个h（x1，x2）再乘以一个系数呢？任何数乘以0当然是0，f（x1，x2）加上0当然保持不变。所以其实就可以等同于求下面这个函数的极值：
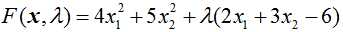
我们对x1，x2以及λ分别求偏导（极值点就是偏导数均为0的点）
解上面的方程组得到x1=1.071，x2=1.286 然后代入f（x1，x2）即可。
这里为什么要多加一个乘子λ呢，试想一下，如果λ是个固定的数（比如-1），我们也能通过上面的方程式1,2求解得到x1，x2，但是我们就得不到方程式3，其实也就是没有约束条件了。所以看到没有，拉格朗日很聪明，他希望我们在求偏导（极值点）以后，还能保留原有的约束条件。我们上面提到，单独对函数求极值不能保证满足约束条件，拉格朗日这么一搞，就能把约束条件带进来，跟求其他变量的偏导结果放在一起，既能满足约束条件，又能保证是约束条件下的极值。借用金星的一句话：完美！
当然这是一个约束条件的情况，如果有多个约束条件呢？那就要用多个不同的λ（想想为什么），正如最上面的那个定义那样，把这些加起来（这些0加起来也是0）。
