heapSort - 堆排序 / 二叉堆

二叉堆是完全二叉树或者是近似完全二叉树。二叉堆满足二个特性：1．父结点的键值总是大于或等于（小于或等于）任何一个子节点的键值。2．每个结点的左子树和右子树都是一个二叉堆（都是最大堆或最小堆）。当父结点的键值总是大于或等于任何一个子节点的键值时为最大堆。当父结点的键值总是小于或等于任何一个子节点的键值时为最小堆。下图展示一个最小堆：

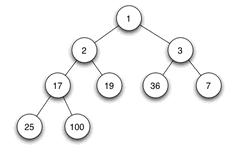
由于其它几种堆（二项式堆，斐波纳契堆等）用的较少，一般将二叉堆就简称为堆。

堆的存储一般都用数组来表示堆，i结点的父结点下标就为 i / 2。它的左右子结点下标分别为2 * i 和 2 * i +1 

堆排序 代码如下 ： 要领 ： 建堆->堆排->堆化[维持]。
#include <iostream>
#include <string>
#include <cstring>
#include <cstdlib>
#include <cstdio>
#include <cmath>
#include <vector>
#include <stack>
#include <deque>
#include <queue>
#include <bitset>
#include <list>
#include <map>
#include <set>
#include <iterator>
#include <algorithm>
#include <functional>
#include <utility>
#include <sstream>
#include <climits>
#include <cassert>
#define BUG puts("here!!!");

using namespace std;

void heapify(int a[], int i, int size) { // 堆化的维持需要用递归
    int ls = 2*i, rs = 2*i + 1;
    int large = i;
    if(ls <= size && a[ls] > a[i]) {
        large = ls;
    }
    if(rs <= size && a[rs] > a[large]) {
        large = rs;
    }
    if(large != i) {
        swap(a[i], a[large]);
        heapify(a, large, size);
    }
}
void buildHeap(int a[], int size) {
    for(int i = size/2; i >= 1; i--) {
        heapify(a, i, size);
    }
}
void heapSort(int a[], int size) {
    buildHeap(a, size);
    int len = size;
    for(int i = len; i >= 2; i--) {
        swap(a[i], a[1]);
        len--;
        heapify(a, 1, len);
    }
}
int main() {
    int a[] = {0, 8, 5, 4, 9, 2, 3, 6}; // 测试用例是 ： 8, 5, 4, 9, 2, 3, 6
    heapSort(a, 7);
    for(int i = 1; i <= 7; i++) {
        cout << a[i] << ' ';
    }
    return 0;
}