数字图像处理第五章
数字图像处理
5.频域图像增强
(1)空域图像增强和频域图像增强结合起来是图像增强技术的完整内容。
(2)频谱:频谱是在频域中反应了图像幅度和相位随频率分布情况的描述图像特征的方法。
① 图像平坦区域对应频谱中低频成分,图像细节内容对应频谱中高频成分。
② 频域图像增强利用了图像在频域中的特有频域特征进行滤波处理。
5.1 滤波基础(理解)
(1)频域值图像的傅里叶变换域;频域图像增强利用图像在频域中特有的频率特征进行滤波处理。
(2)频域滤波的意义:
① 低通滤波允许频谱中低频成分通过,限制高频成分;用于滤除噪声和不必要的细节和纹理,与空域图像平滑等效。
② 高通滤波允许频谱中高频成分通过,限制低频成分;用于突出边缘和细节,与空域图像锐化等效。
(3)频域滤波的核心是 设计滤波器的传递函数 H ( u, v )。
(4)频域滤波的基本流程:
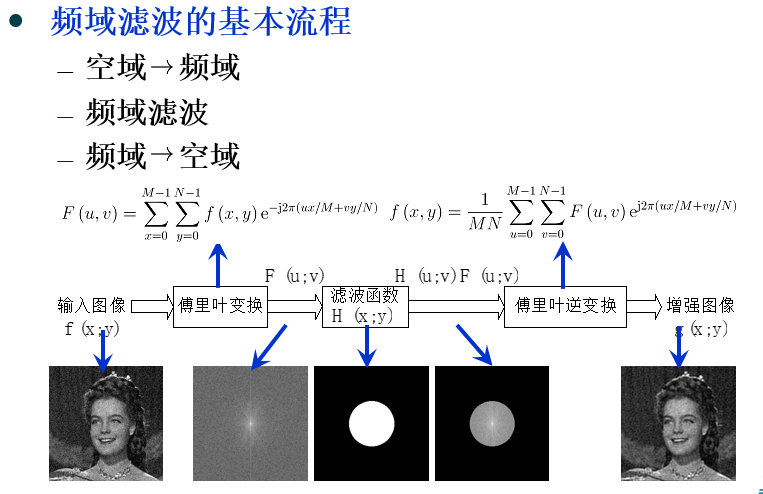
① 计算 f ( x, y ) ( -1 ) x+y(使图像低频成分移到频谱中央) 的二维离散傅里叶变换 F( u, v )。
② 设计频域滤波器传递函数 H( u, v ) ,与输入图像频谱 F( u, v ) 相乘,获得频域滤波结果 G( u, v )。
③ 通过傅里叶逆变换,截取 G( u, v )实部,并乘以( -1 ) x+y,(抵消移位)。
5.2 低通滤波器(理解)
(1)低通滤波器与空域中的平滑模板具有等效作用。
(2)振铃效应:图像灰度剧烈变化的邻域产生灰度震荡的图像失真现象。(截止频率减小,振铃特性增强)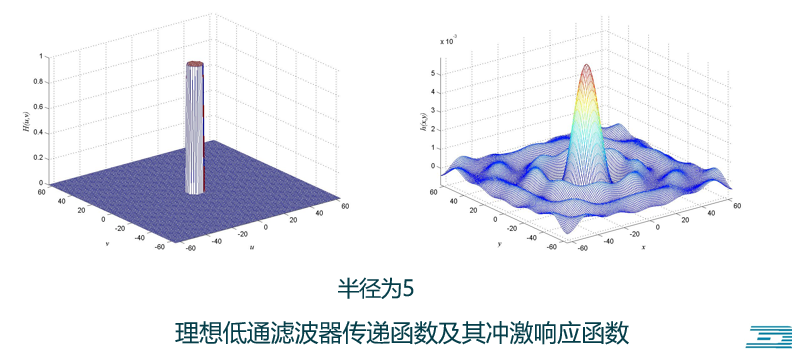
(3)理想低通滤波器(物理不可实现):完全截断频谱中高频部分的滤波器。
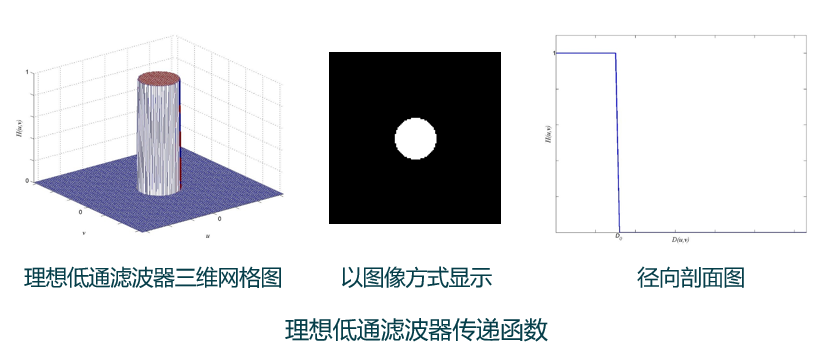
① 随半径增大,保留低频成分越多,滤除高频成分越少,使得模糊程度减弱,图像保留的边缘和细节越多。
(4)巴特沃斯低通滤波器(物理可实现):
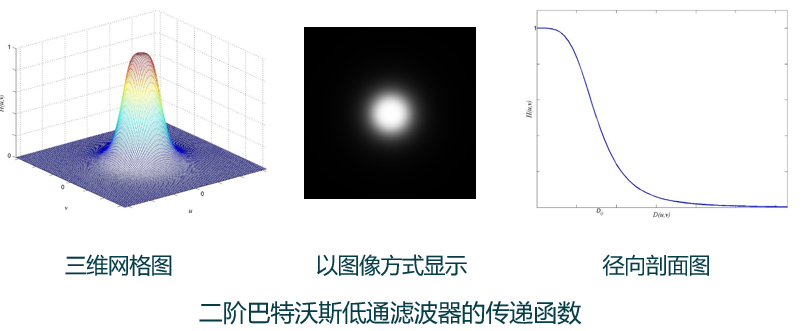
① 一阶巴特沃斯低通滤波器没有振铃现象。
② 随着阶数增加,接近理想低通滤波器,振铃现象越明显。
③ 二阶巴特沃斯低通滤波器在图像平滑与可接受的振铃效应之间做出了比较好的折中。(用于去除均值为0、方差为0.01的高斯噪声)
④ 截止频率越高,滤除的高频部分减少,模糊程度减弱,降噪能力也减弱。
(5)指数低通滤波器(物理可实现):
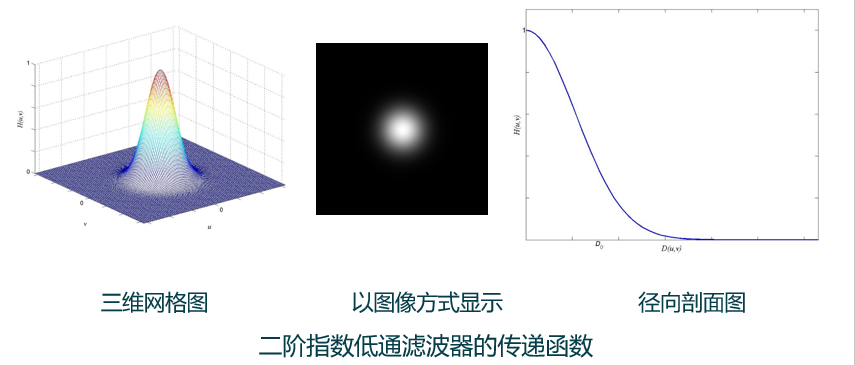
① 滤波器的阶数越高,从通带到阻带振幅衰减速度越快。
② 一阶指数低通滤波器没有振铃效应。
③ 二阶指数低通滤波器具有高斯函数形式,也称为高斯低通滤波器。二阶指数低通滤波器也没有振铃效应。
④ 随着阶数增加,接近理想滤波器,振铃现象越明显。
⑤ 相比于二阶巴特沃斯低通滤波器,二阶指数低通滤波器滤除的高频成分更多,图像更加模糊。
5.3 高通滤波器(理解)
(1)高通滤波器:允许图像高频成分通过,限制低频成分通过。(图像锐化)
(2)理想高通滤波器:完全截断频谱中的低频部分。理想高通滤波器无法用电子器件实现,且会产生明显的振铃效应。(截止频率越大振铃现象越明显)
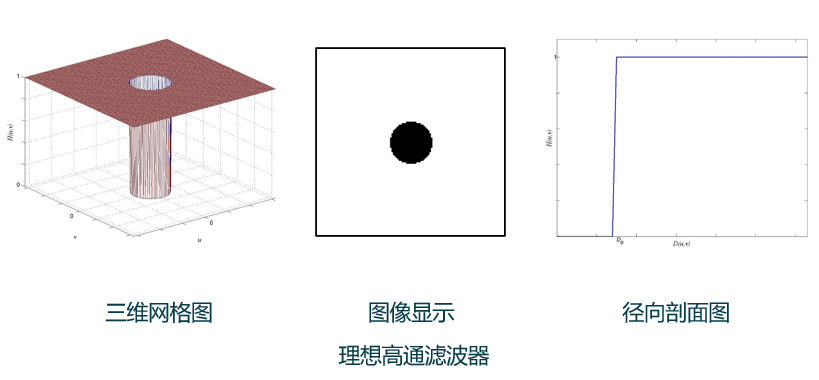
(3)巴特沃斯高通滤波器:

① 阻带与通带之间不是锐截止,之间的过渡比较平滑。
② 随截止频率增大,被滤除的低频成分越多,边缘更加清晰化。
(4)指数高通滤波器:

① 随着截止频率增加,被滤除低频成分越多,边缘更加清晰。
② 相同截止频率的指数高通滤波器比巴特沃斯高通滤波器允许更多的低频成分通过,保留了更多的背景基调。
(5)高通滤波器的局限性:
① 高通滤波器只记录图像变化,不能保持图像能量。
② 低频分量被滤除后,虽然图像各区域边界得到了增强,但原本平滑部分灰度动态范围被压缩,整幅图像比较昏暗。
③ 对②的解决方法:高频强调 / 高频增强(加一个常数到变换函数H(u, v )+ A, A取 0-->1)、后滤波处理(变换完后再进行一次直方图均衡化)
5.4 拉普拉斯频域滤波器(不考)
5.5 带通、带阻、陷波滤波器(理解)
(1)带通滤波器: 允许一定频带信号通过,用于抑制低于 / 高于该频带的信号、噪声干扰。
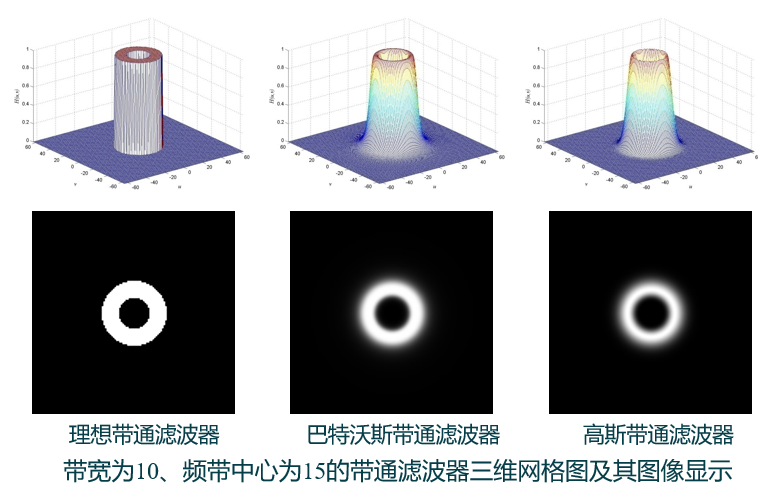
① 理想带通滤波器:具有完全平坦的通带,通带内无增益 / 衰减,完全阻止通带外的所以频率成分。(并不存在)
② 三种带通滤波器比较:
(2)带阻滤波器:限制某一带宽频率成分通过,允许带宽范围外频率成分通过。(与带通滤波器执行相反动作)
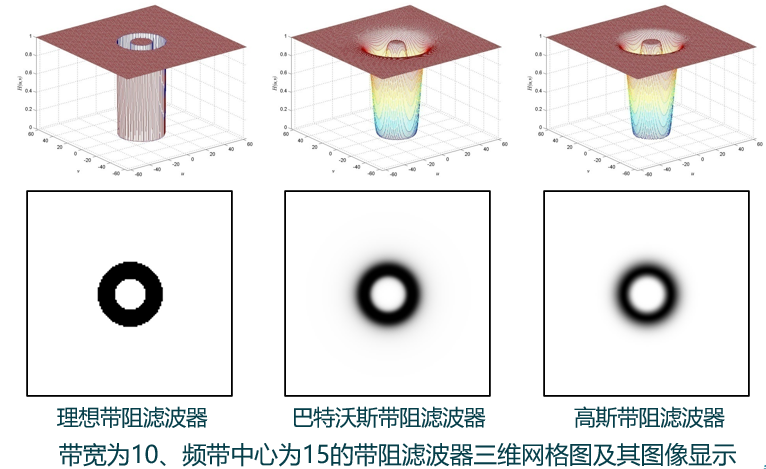
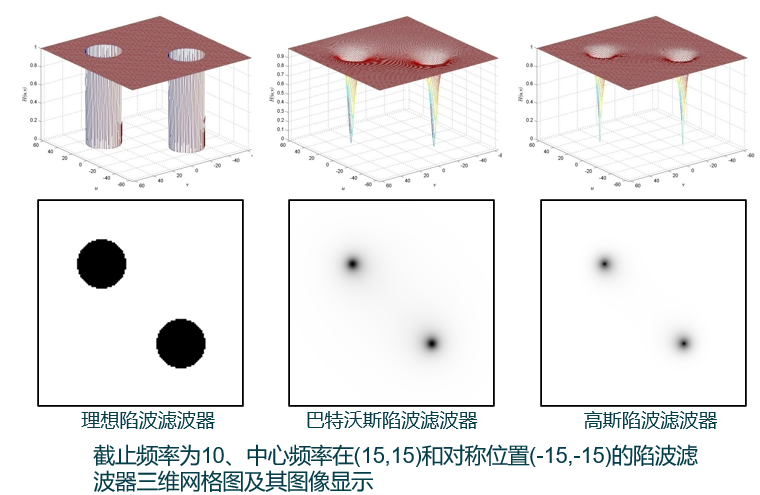
(3)陷波滤波器:一种限制窄带频率范围通过的特殊带阻滤波器,通常用于单一频率的陷波。
5.6 空域滤波与频域滤波关系(理解)
(1)频域滤波器的传递函数和空域冲激响应函数互为傅里叶变换对。
(2)在频域图像增强中,通常利用频率成分和图像内容之间的对应关系,主观判断指定频域滤波器。一些直接在空域中表述困难的增强任务,在频域中变得非常直观。
(3)通过分析频域特性“主要是幅度特性”来分析空域模板作用;借助频域滤波器的设计指导空域模板。
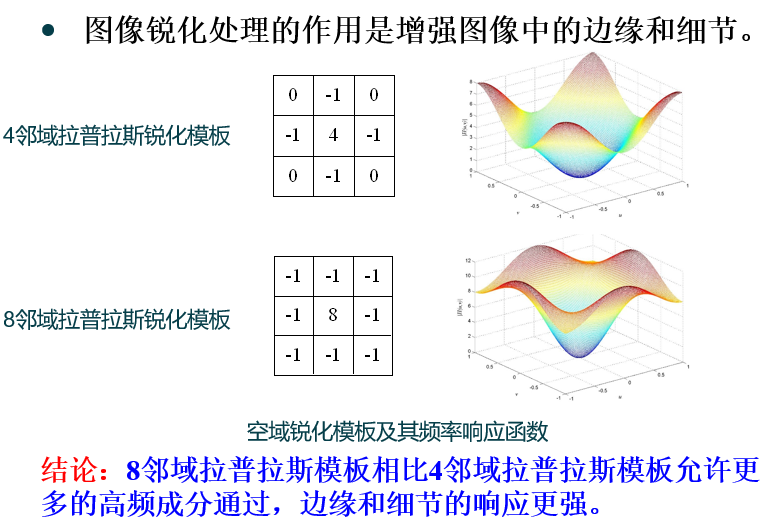
(4)图像平滑处理作用: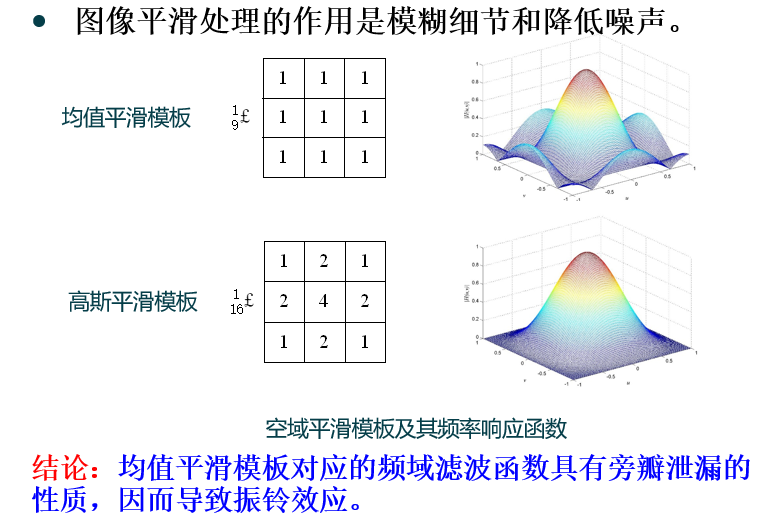
(5)图像锐化处理作用: