Pytorch的cross_entropy为什么等于log_softmax加nll_loss

首先我们要知道nll_loss是怎么算的，看下面的代码

label1 = torch.tensor([0, 3])
pred1 = torch.tensor([
    [0.2, 0.7, 0.8, 0.1],
    [0.1, 0.3, 0.5, 0.7]
    ])
loss = F.nll_loss(pred1, label1)
print(loss)  # 输出 tensor(-0.4500)

如何理解上面的代码？首先明确这是一个分类任务，总共有4个类，上面的代码计算了两条数据，可以认为是bachSize = 2。

	预测为第0类的概率	预测为第1类的概率	预测为第2类的概率	预测为第3类的概率
第1条数据	0.2	0.7	0.8	0.1
第2条数据	0.1	0.3	0.5	0.7

再具体点，每一条数据可以认为是一张图片，每一个类可以认为是该图片是鸡、鸭、鱼、鹅四种动物的概率。label1 = [0, 3]表示两条数据分别属于第0类和第3类，相当于下面的情况。

第1条数据	第0类	第1类	第2类	第3类
预测概率	0.2	0.7	0.8	0.1
实际概率	1	0	0	0

 

第2条数据	第0类	第1类	第2类	第3类
预测概率	0.1	0.3	0.5	0.7
实际概率	0	0	0	1

现在对问题的定义应该比价清楚了，接下来是nll_loss怎么算的，用公式不太好写，这里就用文字描述了：真实类别的预测概率的平均值乘负一。两条数据的真实标签分别是第0类和第3类，相应的预测概率分别为0.2和0.7，平均值为0.45，再乘负一，得0.45，与程序输出情况一致。其中求平均值是因为程序默认reduction='mean'

可以看出来nll_loss只能求每条数据只属于一个类别的情况（我目前理解是这样的），不能出现一条数据既属于第0类，又属于第1类。

同样适用上面的数据，我们计算cross_entropy

label3 = torch.tensor([
    [1, 0, 0, 0],
    [0, 0, 0, 1]
], dtype = torch.float32)
pred3 = torch.tensor([
    [0.2, 0.7, 0.8, 0.1],
    [0.1, 0.3, 0.5, 0.7]
    ])
loss = F.cross_entropy(pred3, label3)
print(loss)  # 输出 tensor(1.3965)

上面的label3代表数据是每个类别的真实概率是多少，跟上面的两个表格一样。label3 也可以用indices（也就是指明属于哪个类别），即 label3 = torch.tensor([0,3])，两者是等价的。

下面探讨如何用log_softmax和nll_loss组合出cross_entropy，代码如下：

label2 = torch.tensor([0, 3])
pred2 = torch.tensor([
    [0.2, 0.7, 0.8, 0.1],
    [0.1, 0.3, 0.5, 0.7]
    ])
pred2 = F.log_softmax(pred2, dim = 1)    # dim = 1是横着四个元素和为1， dim = 0是竖着两个元素和为1
loss = F.nll_loss(pred2, label2)
print(loss)  # 输出 tensor(1.3965)

这里比第一次的代码多了一句 pred2 = F.log_softmax(pred2, dim = 1)。log_softmax的意思是先softmax，再log(实际是ln，以e为底的log)。log用来保证最终结果为正（softmax压缩到区间[0,1]）

为了更深刻的理解，我们接下来手算一下。

原始数据1	0.2	0.7	0.8	0.1
softmax后	0.1860	0.3067	0.3390	0.1683
log后(ln)	-1.682	-1.1818	-1.0817	-1.7820

 

原始数据2	0.1	0.3	0.5	0.7
softmax后	0.1807	0.2207	0.2695	0.3292
log后(ln)	-1.7109	-1.5109	-1.3111	-1.1110

按照nll_loss的计算方法：真实类别的预测概率的平均值乘负一：-1 * (-1.682 + -1.1110) / 2 = 1.3965，与程序输出结果一致。

如果cross_entropy时，每条数据可以同时属于多个类别，又该如何计算呢？如下面的代码，第一条数据同时属于0，1类别，第二条数据同时属于2，3类别。

label4 = torch.tensor([
    [1, 1, 0, 0],
    [0, 0, 1, 1]
], dtype = torch.float32)
pred4 = torch.tensor([
    [0.2, 0.7, 0.8, 0.1],
    [0.1, 0.3, 0.5, 0.7]
    ])
loss = F.cross_entropy(pred4, label4)
print(loss)  # 输出 tensor(2.6430)

这里我们先明确cross_entropy的计算方法，下面是公式。其中pi是真实概率，qi是预测概率。

 

 

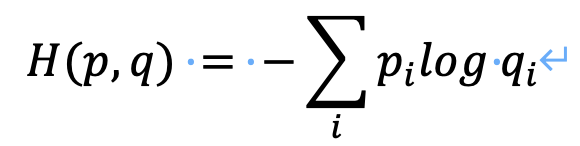
Pytorch的cross_entropy自动对输入(input)，也就是上面的pred4进行log_softmax，按照上面的计算，pred4经过处理变成

[[-1.682, -1.1818, -1.0817, -1.7820],

[-1.7109, -1.5109, -1.3111, -1.1110]]

按照公式H(p, q) = -(1 * -1.682 + 1 * -1.1818 + 1 * -1.3111 + 1 * -1.1110) = 5.2859，默认要求平均，因为是两条数据所以除以2等于2.64295，与程序输出2.6430基本一致。

用nll_loss+log_softmax的方法计算代码如下，感觉有些麻烦。

pred5 = F.log_softmax(pred4, dim = 1)
loss = F.nll_loss(pred5[0].unsqueeze(0), torch.tensor([0])) + F.nll_loss(pred5[0].unsqueeze(0), torch.tensor([1])) + F.nll_loss(pred5[1].unsqueeze(0), torch.tensor([2])) + F.nll_loss(pred5[1].unsqueeze(0), torch.tensor([3]))
print(loss/2)  # 输出 tensor(2.6430)

其中的unsqueeze(0)表示增加一个维度，也就是加一层方括号。