树的节点、度数、高度、深度、遍历
1.节点的度与树的度
节点的度:结点拥有的子树数目称为结点的度,叶子结点 就是度为0的结点
树的度:树内各结点的度的最大值
分支节点:度不为0的节点
--------------------------------------------------
节点数n=n0+n1+n2, ( n0:度为0的结点数,n1:度为1的结点 n2:度为2的结点数。 n是总结点)
非空二叉树,n0=n2+1;
当节点数n为奇数,无度为1的节点;节点n为偶数,有一个度为1的节点;
--------------------------------------------------
分支数=n-1 =1*n1+ 2*n2+3*n3
n0+n1+n2+n3 = n = 分支数+1 = 1*n1+ 2*n2+3*n3+1
2.树的深度与高度
节点 ni 的深度:从根节点到 ni 的的唯一路径长。即,节点 ni 所在的层次(根节点为0层),树的深度 = 树中节点的最大层次。
节点 ni 的高度:从 ni 到一片树叶的最长路径长。即,叶子节点的高度为0,树的高度 = 根的高度。
树的深度 = 树的高度
高度为h的二叉树至少2^h个节点,至多有2^(h+1)-1 个节点。
含有n≥1 个节点的二叉树的高度范围:[ | log2 n」,n-1]
3.完全二叉树:
只有最下面的两层结点度小于2,并且最下面一层的结点都集中在该层最左边的若干位置。
有 n 个节点的完全二叉树的高度(深度)为 | log2 n」
完全二叉树第 n 层上至多 2^(n+1)个节点
完全二叉树第 n 层上节点编号: 2^n - 2^(n+1)-1
--------------------------------------------------
例1:在一棵具有n个结点的完全二叉树中,树枝结点的最大编号为( B ).假定树根结点的编号为1
A.(n-1)/2 B.n/2 C.n/2-1
例2:编号13的左兄弟节点是( A ),右兄弟节点是( B )
A.12 B.14
层数 = | log2 n」= 3
3层编号范围 8-15
例3:若一棵完全二叉树有768 个结点,则该二叉树中叶结点的个数是( C )。
A.257 B.258 C.384 D.385
n=n0+n1+n2;
当节点数n为奇数,无度为1的节点;节点n为偶数,有一个度为1的节点,n1 = 1;
768=n0+n1+n2;n2=n0-1;
所以n0=384
例4:一颗完全二叉树第六层有8个叶结点(根为第一层),则结点个数最多有()个。
正确答案: D 你的答案: B (错误)
A.39 B.72 C.104 D.111
二叉树第k层最多有2的(k-1)次方个节点
1-6层 : 2^6-1=63个
7 层: 24*2 = 48 第七层的节点是第六层的左边24个的子节点(因为最右边8个是叶子节点),所以是48个
所以,63+ 48 = 111
例5:将一棵有100个结点的完全二叉树从根这一层开始,开始进行层次遍历编号,那么编号最小的叶节点的编号为(根节点为1)
正确答案: C 你的答案: A (错误)
49 50 51 52
解析1:完全二叉树中,对于编号为i的父结点,左孩子编号为2*i',右孩子编号为2*i+1;
编号为100的节点对应的父节点编号为50,故最小叶子节点编号为51
解析2:深度为6的满二叉树的节点数为 2^6 - 1 = 63;
深度为7的满二叉书的节点数为 2^7 - 1 = 127;
因此含有100个节点的完全二叉树的深度为7,叶子节点分布在第6层和第7层。
第七层叶子节点数为:100 - 63 = 37;
37 / 2 = 18余1;
因此,第6层的前18个节点是2度节点,第19个节点是1度节点即只有左子树,没有右子树,即第6层前19个节点为非叶子节点,之后为叶子节点。
因此编号最小的叶子节点编号为:2 ^5 - 1 + 19 + 1 = 51.
其中,2^5 - 1位前5层非叶子节点数(由满二叉树的节点计算公式得出)
4.满二叉树:
是一颗完全二叉树;除了叶结点外每一个结点都有左右子叶且叶结点都处在最底层。
第 n 层有 2^(n+1)-1 个节点
深度为k,且有 2^(k+1)-1个节点。
5.堆:
是一颗完全二叉树;
大顶堆:左右子树的结点值都小于根结点值,左右子树都是大顶堆。
小顶堆:左右子树的结点值都大于根结点值,左右子树都是小顶堆。
6.二叉排序树(二叉查找树):
左子树上的值都小于根结点的值,右子树上的值都大于根结点得值,左右子树都是二叉排序树。
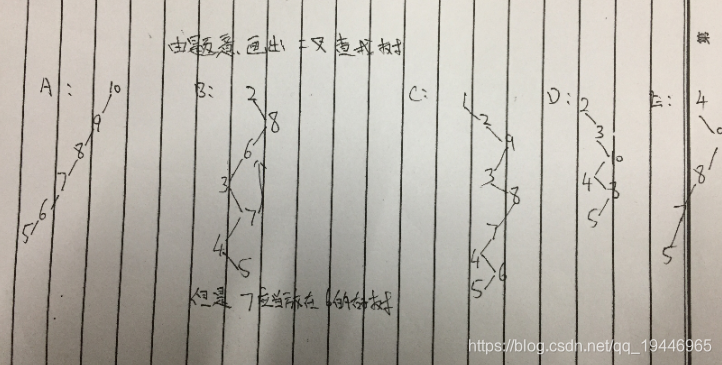
例:将整数序列(7-2-4-6-3-1-5)按所示顺序构建一棵二叉排序树a(亦称二叉搜索树),之后将整数8按照二叉排序树规则插入树a中,请问插入之后的树a中序遍历结果是____。
正确答案: A 你的答案: A (正确)
A.1-2-3-4-5-6-7-8 B.7-2-1-4-3-6-5-8 C.1-3-5-2-4-6-7-8
D.1-3-5-6-4-2-8-7 E.7-2-8-1-4-3-6-5 F.5-6-3-4-1-2-7-8
不用看题目直接看答案排除,二叉排序树的中序遍历一定有序
|
7 |
|||
|
2 |
8 |
||
|
1 |
4 |
||
|
3 |
6 |
||
|
5 |
例:假设某棵二叉查找树的所有键均为1到10的整数,现在我们要查找5。下面____不可能是键的检查序列。
A.10,9,8,7,6,5 B.2,8,6,3,7,4,5 C.1,2,9,3,8,7,4,6,5 D.2,3,10,4,8,5 E.4,9,8,7,5 F.以上均正确
7.平衡二叉树(ALV):
是一颗二叉排序树;左子树和右子树的高度差值不超过1,左右子树都为平衡二叉树。
插入,查找,删除的时间复杂度最好情况和最坏情况都维持在O(logN)
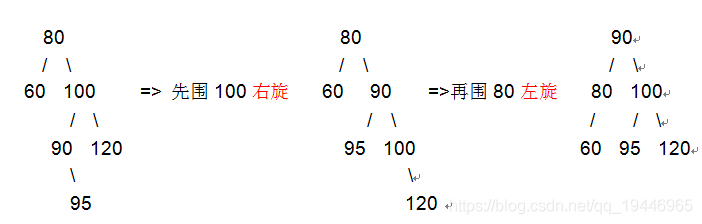
插入操作:在平衡二叉树中插入结点与二叉查找树最大的不同在于要随时保证插入后整棵二叉树是平衡的。那么调整不平衡树的基本方法就是: 旋转,基本思路都是转换到左旋和右旋。
1) 右旋: 在最小平衡子树根节点平衡因子>=2且在根节点的左孩子的左孩子插入元素,进行右旋
2) 左旋: 在最小平衡子树根节点平衡因子>=-2且在根节点的右孩子的右孩子插入元素,进行左旋。
3) 右左:最小平衡子树根节点(80)的右孩子(100)的左孩子(90)的子节点(95)插入新元素,先绕根节点的右孩子节点(100)右旋,再围根节点(80)左旋
4) 左右:在最小平衡子树根节点(80)的左孩子(50)的右孩子(70)的子节点插入新元素,先绕根节点的左孩子节点(50)右旋,再围根节点(80)左旋
8.红黑树:
与AVL类似,平衡二叉B树,并不追求“完全平衡”——它只要求部分地达到平衡要求,降低了对旋转的要求,从而提高了性能。
红黑树的算法时间复杂度和AVL相同
红黑树的特性:
(1)每个节点或者是黑色,或者是红色。
(2)根节点是黑色。
(3)每个叶子节点(NIL)是黑色。 [注意:这里叶子节点,是指为空(NIL或NULL)的叶子节点!]
(4)如果一个节点是红色的,则它的子节点必须是黑色的。
(5)从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。
注意:
- (特性(3)中的叶子节点,是只为空(NIL或null)的节点。
- 特性(5),确保没有一条路径会比其他路径长出俩倍。因而,红黑树是相对是接近平衡的二叉树。
根据被插入节点的父节点的情况,可以将"当节点z被着色为红色节点,并插入二叉树"划分为三种情况来处理。
① 情况说明:被插入的节点是根节点。
处理方法:直接把此节点涂为黑色。
② 情况说明:被插入的节点的父节点是黑色。
处理方法:什么也不需要做。节点被插入后,仍然是红黑树。
③ 情况说明:被插入的节点的父节点是红色。
处理方法:那么,该情况与红黑树的“特性(5)”相冲突。这种情况下,被插入节点是一定存在非空祖父节点的;进一步的讲,被插入节点也一定存在叔叔节点(即使叔叔节点为空,我们也视之为存在,空节点本身就是黑色节点)。理解这点之后,我们依据"叔叔节点的情况",将这种情况进一步划分为3种情况(Case)。
|
|
现象说明 |
处理策略 |
|
Case 1 |
当前节点的父节点是红色,且当前节点的祖父节点的另一个子节点(叔叔节点)也是红色。 |
(01) 将“父节点”设为黑色。 (02) 将“叔叔节点”设为黑色。 (03) 将“祖父节点”设为“红色”。 (04) 将“祖父节点”设为“当前节点”(红色节点);即,之后继续对“当前节点”进行操作。 |
|
Case 2 |
当前节点的父节点是红色,叔叔节点是黑色,且当前节点是其父节点的右孩子 |
(01) 将“父节点”作为“新的当前节点”。 (02) 以“新的当前节点”为支点进行左旋。 |
|
Case 3 |
当前节点的父节点是红色,叔叔节点是黑色,且当前节点是其父节点的左孩子 |
(01) 将“父节点”设为“黑色”。 (02) 将“祖父节点”设为“红色”。 (03) 以“祖父节点”为支点进行右旋。 |
上面三种情况(Case)处理问题的核心思路都是:将红色的节点移到根节点;然后,将根节点设为黑色。下面对它们详细进行介绍。
红黑树的应用
红黑树的应用比较广泛,主要是用它来存储有序的数据,它的时间复杂度是O(lgn),效率非常之高。
例如,Java集合中的TreeSet和TreeMap,C++ STL中的set、map,以及Linux虚拟内存的管理,都是通过红黑树去实现的。
2-3-4树
2-3-4树和红黑树一样,也是平衡树。只不过不是二叉树,它的子节点数目可以达到4个。
每个节点存储的数据项可以达到3个。名字中的2,3,4是指节点可能包含的子节点数目。具体而言:
- 1、若父节点中存有1个数据项,则必有2个子节点。
- 2、若父节点中存有2个数据项,则必有3个子节点。
- 3、若父节点中存有3个数据项,则必有4个子节点。
也就是说子节点的数目是父节点中数据项的数目加一。因为以上三个规则,使得除了叶结点外,其他节点必有2到4个子节点,不可能只有一个子节点。所以不叫1-2-3-4树。而且2-3-4树中所有叶结点总是在同一层。
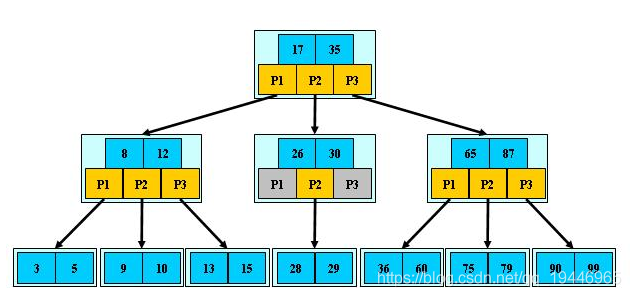
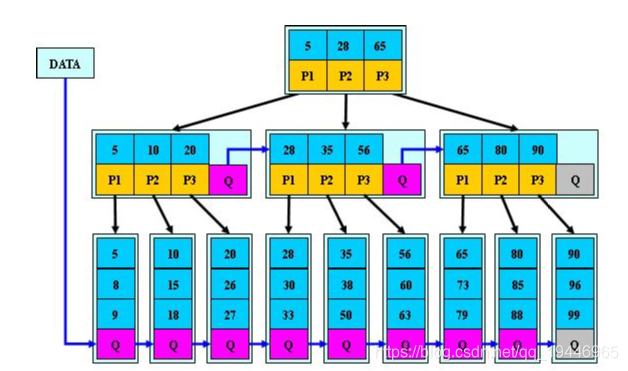
9.B树:
是一种多路搜索树(并不是二叉的):
1.定义任意非叶子结点最多只有M个儿子;且M>2;
2.根结点的儿子数为[2, M];
3.除根结点以外的非叶子结点的儿子数为[M/2, M];
4.每个结点存放至少M/2-1(取上整)和至多M-1个关键字;(至少2个关键字)
5.非叶子结点的关键字个数=指向儿子的指针个数-1;
6.非叶子结点的关键字:K[1], K[2], …, K[M-1];且K[i] < K[i+1];
7.非叶子结点的指针:P[1], P[2], …, P[M];其中P[1]指向关键字小于K[1]的
子树,P[M]指向关键字大于K[M-1]的子树,其它P[i]指向关键字属于(K[i-1], K[i])的子树;
8.所有叶子结点位于同一层;
如:(M=3)
B-树的特性:
1.关键字集合分布在整颗树中;
2.任何一个关键字出现且只出现在一个结点中;
3.搜索有可能在非叶子结点结束;
4.其搜索性能等价于在关键字全集内做一次二分查找;
5.自动层次控制;
由于限制了除根结点以外的非叶子结点,至少含有M/2个儿子,确保了结点的至少
利用率,其最底搜索性能为:O(logn)
其中,M为设定的非叶子结点最多子树个数,N为关键字总数;
所以B-树的性能总是等价于二分查找(与M值无关),也就没有B树平衡的问题;
由于M/2的限制,在插入结点时,如果结点已满,需要将结点分裂为两个各占
M/2的结点;删除结点时,需将两个不足M/2的兄弟结点合并
例:在一棵具有15个关键字的4阶B树中,含关键字的结点数最多是 ( D )
A.5 B.6 C.10 D.15
根据m阶B-树定义,
- 根结点至多有m棵子树,即至多有m-1个关键字,若根结点不是终端结点,则至少有2棵子树
- 除根以外的所有非叶结点至少有 ⌈ m/ 2 ⌉ 棵子树,即至少含有 ⌈ m/ 2 ⌉ − 1 个关键字⌈ 4/ 2 ⌉ − 1 = 1
因此,根据题干,只需要满足根结点有1个关键字。非叶结点至少1个关键字,即,一个结点一个关键字时,结点数最多,最多为15个结点。
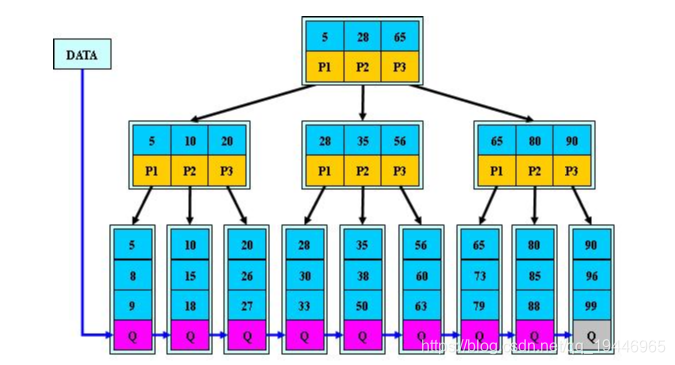
10.B+树:
B+树是B-树的变体,也是一种多路搜索树
由于B+树的数据都存储在叶子结点中,分支结点均为索引,方便扫库,只需要扫一遍叶子结点即可,但是B树因为其分支结点同样存储着数据,我们要找到具体的数据,需要进行一次中序遍历按序来扫,所以B+树更加适合在区间查询的情况,所以通常B+树用于数据库索引,而B树则常用于文件索引。
B+树是B-树的变体,也是一种多路搜索树:
1.其定义基本与B-树同,除了:
2.非叶子结点的子树指针与关键字个数相同;
3.非叶子结点的子树指针P[i],指向关键字值属于[K[i], K[i+1])的子树(B树是开区间);
5.为所有叶子结点增加一个链指针;
6.所有关键字都在叶子结点出现;
如:(M=3)
B+的特性:
1.所有关键字都出现在叶子结点的链表中(稠密索引),且链表中的关键字恰好
是有序的;
2.不可能在非叶子结点命中;
3.非叶子结点相当于是叶子结点的索引(稀疏索引),叶子结点相当于是存储
(关键字)数据的数据层;
4.更适合文件索引系统
例:有B+Tree/Hash_Map/STL Map三种数据结构。对于内存中数据,查找性能较好的数据结构是(),对于磁盘中数据,查找性能较好的数据结构是()。
正确答案: A 你的答案: D (错误)
A.Hash_Map/B+Tree B.STL_Map/B+Tree C.STL_Map/Hash_Map D.B+Tree/Hash_Map
11.B*树:
是B+树的变体,在B+树的非根和非叶子结点再增加指向兄弟的指针
B*树定义了非叶子结点关键字个数至少为(2/3)*M,即块的最低使用率为2/3(代替B+树的1/2);
B+树的分裂:当一个结点满时,分配一个新的结点,并将原结点中1/2的数据复制到新结点,最后在父结点中增加新结点的指针;B+树的分裂只影响原结点和父结点,而不会影响兄弟结点,所以它不需要指向兄弟的指针;
B*树的分裂:当一个结点满时,如果它的下一个兄弟结点未满,那么将一部分数据移到兄弟结点中,再在原结点插入关键字,最后修改父结点中兄弟结点的关键字(因为兄弟结点的关键字范围改变了);如果兄弟也满了,则在原结点与兄弟结点之间增加新结点,并各复制1/3的数据到新结点,最后在父结点增加新结点的指针;所以,B*树分配新结点的概率比B+树要低,空间使用率更高;
总结:
B树:多路搜索树,每个结点存储M/2到M个关键字,非叶子结点存储指向关键字范围的子结点;所有关键字在整颗树中出现,且只出现一次,非叶子结点可以命中;
B+树:在B树基础上,为叶子结点增加链表指针,所有关键字都在叶子结点中出现,非叶子结点作为叶子结点的索引;B+树总是到叶子结点才命中;
B*树:在B+树基础上,为非叶子结点也增加链表指针,将结点的最低利用率从1/2提高到2/3;
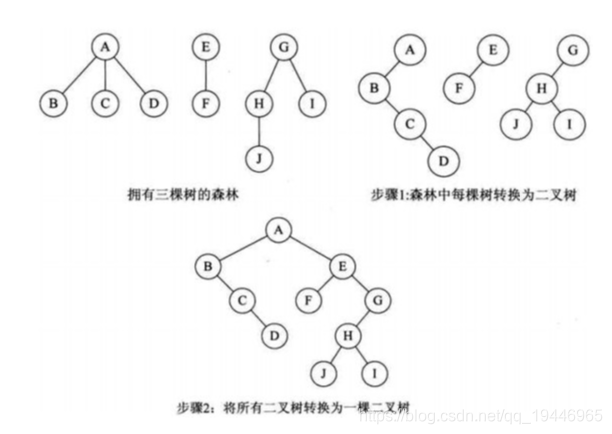
12.树和森林相互转换
例:把一棵树转换为二叉树后,这棵二叉树的形态是( A )
A.唯一的 B.有多种 C.有多种,根结点没有左孩子 D.有多种,根结点没有右孩子
树变二叉树过程:
1.给兄弟加线 2.去掉长子外的线 3.层次调整
森林变二叉树:
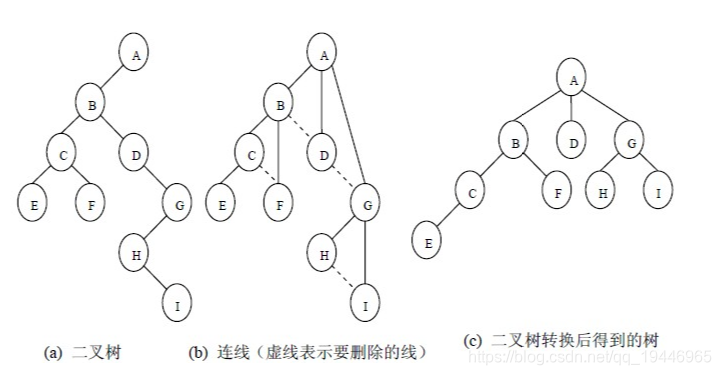
二叉树转换为树
二叉树转换为树是树转换为二叉树的逆过程,其步骤是:
(1)若某结点的左孩子结点存在,将左孩子结点的右孩子结点、右孩子结点的右孩子结点……都作为该结点的孩子结点,将该结点与这些右孩子结点用线连接起来;
(2)删除原二叉树中所有结点与其右孩子结点的连线;
(3)整理(1)和(2)两步得到的树,使之结构层次分明。
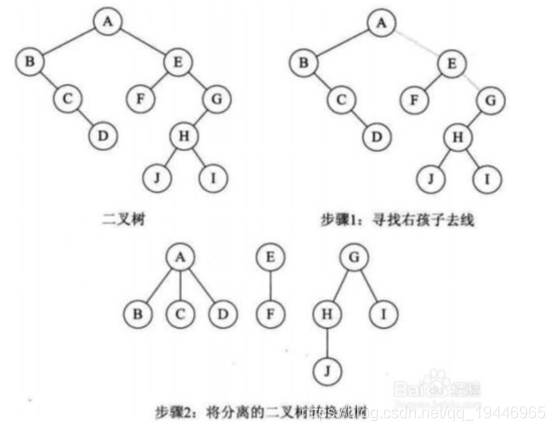
二叉树转换为森林
假如一棵二叉树的根节点有右孩子,则这棵二叉树能够转换为森林,否则将转换为一棵树。
(1)从根节点开始,若右孩子存在,则把与右孩子结点的连线删除。再查看分离后的二叉树,若其根节点的右孩子存在,则连线删除…。直到所有这些根节点与右孩子的连线都删除为止。
(2)将每棵分离后的二叉树转换为树。
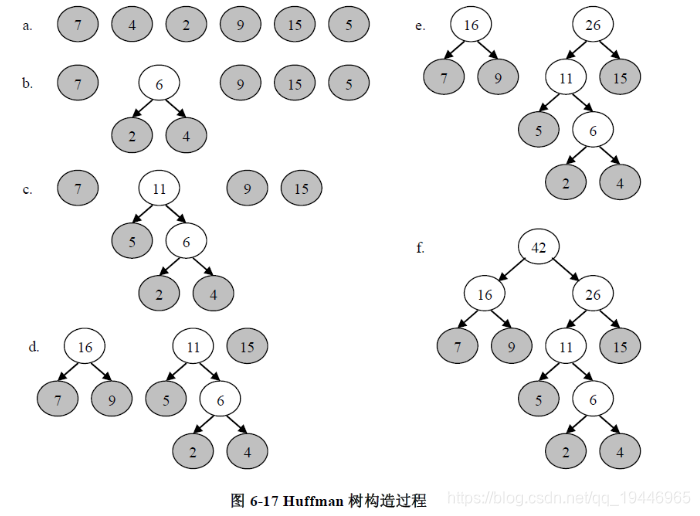
13.哈夫曼树及编码(Huffman)
构造哈夫曼树步骤是,选择两个权值最小的点构造树,新树根权值为左右子树权值之和,新的权值放回到序列中,继续按照上述不走构造树,直到只有一颗树为止。 树带权路径长度 就是每个叶子结点的权值*深度之和。
例: 假设有一组权值{7, 4, 2, 9, 15, 5},试构造以这些权值为叶子的Huffman树,求带权路径长度。
带权路径长度 = (2+4)*4 + 5*3 +(7+9+15)*2 = 101
求ABACCDA的最短编码长度(Huffman编码)?
权重A:3,B:1,C:2,D:1
编码长度 = (1+1)*3 + 2*2 + 3*1 = 13
例:中序遍历二叉链存储的二叉树时,一般要用堆栈;中序遍历检索二叉树时,也必须使用堆栈(×)
二叉链存储法也叫孩子兄弟法,左指针指向左孩子,右指针指向右兄弟。而中序遍历的顺序是左孩子,根,右孩子。这种遍历顺序与存储结构不同,因此需要堆栈保存中间结果。
检索二叉树 增加了指向前驱结点和指向后继节点的标志,因此在遍历时无需用栈
例:利用二叉链表存储树,则根结点的右指针是()
正确答案: C 你的答案: B (错误)
A.指向最左孩子 B.指向最右孩子 C.空 D.非空
二叉链表根节点的左指针指向根节点左孩子,右指针指向根节点的兄弟。树的根节点没有兄弟,因此为空。
例:一个包含 n 个节点的四叉树,每个节点都有四个指向孩子节点的指针,这 4n 个指针中有多少个空指针?
正确答案: D 你的答案: D (正确)
A.2n+1 B.3n-1 C.3n D.3n+1
n个结点为一棵树则有n-1条边,因此有n-1个非空指针
空指针个数4*n-(n-1)=3*n+1
令n=1,空指针有四个!
例:用三叉链表作二叉树的存储结构,当二叉树中有n个结点时,有()个空指针。
正确答案: C 你的答案: A (错误)
A.n+1 B.n C.n+2 D.n-1
对于有n个节点的树结构,有n-1条边,每条边是孩子节点指向父节点的指针,也是父节点指向孩子节点的孩子指针, 所以一共是2(n-1)个指针,总的指针就是3n-2(n-1)=n+2
例:若平衡二叉树的高度为6,且所有非叶结点的平衡因子均为 1,则该平衡二叉树的结点总数为( B )。
A.12 B.20 C.32 D.33
平衡二叉树上所有结点的平衡因子只可能是 -1,0 或 1。
最小二叉平衡树的节点的公式如下 F(n)=F(n-1)+F(n-2)+1
或者说深度为n的平衡二叉树,至少有F(n)个结点。
Fibonacci(斐波那契)数列,1是根节点,F(n-1)是左子树的节点数量,F(n-2)是右子树的节点数量。注意:F(0)=0,F(1)=1。
得知平衡二叉树的最少的结点的个数为20。
例:以下这些树中,属于平衡二叉树的有哪些?
正确答案: A E 你的答案: C E (错误)
红黑树 二叉查找树 B+树 八叉树 完全二叉树
二叉查找树可以是任意高度,甚至退化为链表
八叉树和B+树不是二叉树
红黑树是平衡二叉树
完全二叉树左右子树的高度最多差1,也是平衡二叉树
n个结点为一棵树则有n-1条边
求最小生成树的Prim算法和Kruskal算法,Huffman树都是漂亮的贪心算法。







 浙公网安备 33010602011771号
浙公网安备 33010602011771号