万能的搜索--之BFS（三）

接着（一）start

（二）广度优先搜索（BFS）

广度优先搜索（又称宽度优先搜索算法）是最简便的图的搜索算法之一，这一算法也是很多重要的图的算法的原型。   Dijkstra单源最短路径算法和Prim最小生成树算法都采用了和宽度优先搜索类似的思想。其别名又叫BFS，属于一种盲目搜寻法，目的是系统地展开并检查图中的所有节点，以找寻结果。换句话说，它并不考虑结果的可能位置，彻底地搜索整张图，直到找到结果为止。

 

广搜的核心思想就是：从初始结点开始，产生第一层节点，检查目标结点是否在这些后继结点之中，没有，就扩展第一层节点，若没有，用产生式规则得到第二层节点；检查目标结点是否在这些后继结点之中，没有，就扩展第 二层节点……像这样以此扩展节点、检查，直到发现目标结点为止。

 

 

优点：
找到的第一个解一定是最优解
缺点：
占用空间比较大

 

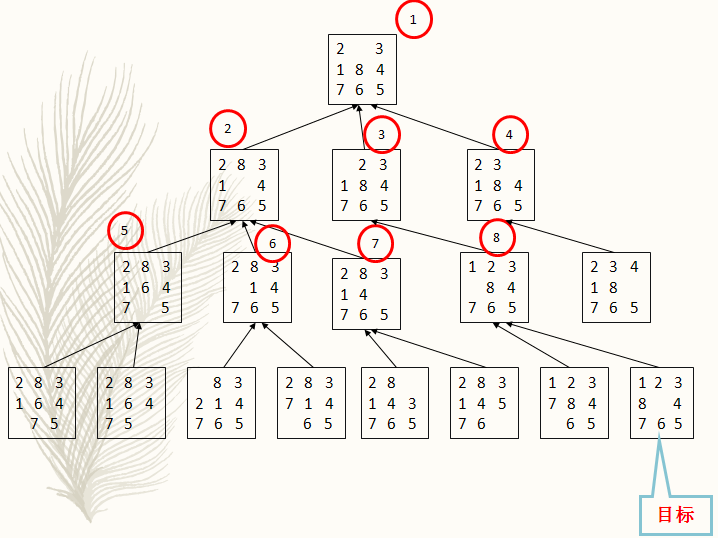
经典题：八数码问题、

在3×3的棋盘，摆有八个棋子，每个棋子上标有1至8的某一数字，不同棋子上标的数字不相同。棋盘上还有一个空格，与空格相邻的棋子可以移到空格中。
给出一个初始状态和一个目标状态，找出一种从初始转变成目标状态的移动棋子步数最少的移动步骤。

伪代码：

初始状态加入队列
while 队列非空
获取当前队首状态
for 当前状态可能的下一状态st
if 该状态之前未被搜索到
if 该状态为目标状态
输出并退出
else
加入队尾

 

如何判重：

如何判断某一状态之前是否出现过？
将状态转换为一个数字（Hash）
举例
abac（字符串）转化为数字
0 * 26^3 + 1 * 26^2 + 0 * 26 + 2
矩阵转化为数字

具体代码实现：

#include<stdio.h>

struct node
{
    int xy[3][3];
    int dir;
};
struct node sh[102], end;
int count = 1;

void init()
{
    printf("输入起始节点的位置:\n");
    int i, j;
    for (i = 0; i < 3; i++)
        for (j = 0; j < 3; j++)
            scanf("%d", &sh[0].xy[i][j]);
    sh[0].dir = -1;
    printf("输入目标节点的位置:\n");
    for (i = 0; i < 3; i++)
        for (j = 0; j < 3; j++)
            scanf("%d", &sh[101].xy[i][j]);
    sh[101].dir = -1;
}

//找出0的位置
int loction(int num)
{
    int i;
    for (i = 0; i < 9; i++)
        if (sh[num].xy[i / 3][i % 3] == 0) return i;
}


//进行标记
long long sign(int num)
{
    long long  sum;
    sum = sh[num].xy[0][0]*100000000 + sh[num].xy[0][1]*10000000 + sh[num].xy[0][2]*1000000 + sh[num].xy[1][0]*100000 + sh[num].xy[1][1]*10000 + sh[num].xy[1][2]*1000 + sh[num].xy[2][0]*100 + sh[num].xy[2][1]*10 + sh[num].xy[2][2];
    return sum;
}

void mobile(int num)
{

    int temp;
    int loc;
    int up = 1, down = 1, left = 1, right = 1;
    loc = loction(num);
    int stand = sh[num].dir;
    //dir的0 1 2 3分别代表左 上 右 下
    if (loc / 3 != 0 && stand != 1)
    {
        sh[count] = sh[num];
        temp = sh[count].xy[loc / 3][loc % 3];
        sh[count].xy[loc / 3][loc % 3] = sh[count].xy[loc / 3 - 1][loc % 3];
        sh[count].xy[loc / 3 - 1][loc % 3] = temp;
        sh[count].dir = 3;
        count++;
    };
    if (loc / 3 != 2 && stand != 3)
    {
        sh[count] = sh[num];
        temp = sh[count].xy[loc / 3][loc % 3];
        sh[count].xy[loc / 3][loc % 3] = sh[count].xy[loc / 3 + 1][loc % 3];
        sh[count].xy[loc / 3 + 1][loc % 3] = temp;
        sh[count].dir = 1;
        count++;
    }
    if (loc % 3 != 0 && stand != 0)
    {
        sh[count] = sh[num];
        temp = sh[count].xy[loc / 3][loc % 3];
        sh[count].xy[loc / 3][loc % 3] = sh[count].xy[loc / 3][loc % 3 - 1];
        sh[count].xy[loc / 3][loc % 3 - 1] = temp;
        sh[count].dir = 2;
        count++;
    }
    if (loc % 3 != 2 && stand != 2)
    {
        sh[count] = sh[num];
        temp = sh[count].xy[loc / 3][loc % 3];
        sh[count].xy[loc / 3][loc % 3] = sh[count].xy[loc / 3][loc % 3 + 1];
        sh[count].xy[loc / 3][loc % 3 + 1] = temp;
        sh[count].dir = 0;
        count++;
    }

}
void display(int num)
{
    int i, j;
    for (i = 0; i < 3; i++)
    {
        for (j = 0; j < 3; j++)
            printf("%d ", sh[num].xy[i][j]);
        printf("\n");
    }
}

int search()
{
    int i = 0;
    while (1)
    {
        printf("\n");
        display(i);
        printf("\n");
        if (i == 100)
        {
            printf("超出了上限次数\n");
            return 0;
        }
        if (sign(i) == sign(101))
        {
            printf("在第%d次找到了", i);
            display(i);
            return i;
        }
        mobile(i);
        i++;
    }
}

int main()
{
    init();
    search();
    return 0;
}

 

未完.....