旅行

题目大意

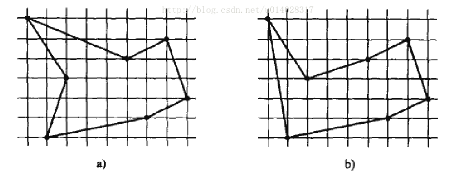
给定平面上n（n≤1000）个点的坐标（按x递增顺序，坐标为正整数），你的任务是设计一条路线，从最左边出发，走到最右边再返回，要求除最左边和最右边的点外，

每个点恰好经过一次，且总路径长度最短。下图给出两种不同方案。答案保留两位小数。

Sample Input
3 
1 1
2 3
3 1
4 
1 1 
2 3
3 1
4 2

 

 Sample Output

6.47
7.89


定义d(i,j)表示1~max(i,j)全部走过，第一个人在i,第二个人在j，还需要走多长的距离。此时规定i>j，还可以规定i,j中只有一个人允许走到i+1这一点。
这样的话可以保证不会出现某些点跳过的情况。状态转移方程如下：
　　　　　　　　　　　　　　　　　　　　d(i,j)=min(d(i+1,j)+dist(i,i+1),d(i+1,i)+dist(j,i+1))

#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
#define ll long long

const int maxn=1000+10;

struct node{
    int x,y;
}p[maxn];

int n;
double ans;
double d[maxn][maxn];

double dist(int i, int j) {
    int dx=p[i].x-p[j].x;
    int dy=p[i].y-p[j].y;
    return sqrt(dx*dx+dy*dy);
}

double dp(int i, int j) {
    double &ans=d[i][j];
    if(ans>0) return ans;
    if(i==n-1) return ans=dist(i,n)+dist(j,n);
    ans=min(dp(i+1,j)+dist(i,i+1),dp(i+1,i)+dist(j,i+1));
    return ans;
}

int main(){
    while(scanf("%d",&n)!=EOF){
        memset(d,0,sizeof(d));
        for(int i=1;i<=n;i++)
        scanf("%d%d",&p[i].x,&p[i].y);
        dp(2,1);
        ans=dist(1,2)+d[2][1];
        printf("%.2lf\n",ans);
    }
    return 0;
}