cf1
1.Codeforces Round #729 (Div. 2) B. Plus and Multiply


题解:枚举 a 的次方,若 n 减去 a 的次方是 b 的整倍数,则 n 满足要求,注意特判 a = 1 与 b = 1 。

#include<cmath> #include<cstdio> #include<cstdlib> #include<iostream> #include<cstring> #include<algorithm> using namespace std; #define ll long long ll T,n,a,b; template<typename T>void inline read(T &aa){ ll ff=1;char cc=getchar();aa=0; while((cc<'0'||cc>'9')&&cc!='-') cc=getchar(); if(cc=='-') ff=-1,cc=getchar(); while(cc<='9'&&cc>='0') aa=aa*10+cc-48,cc=getchar(); aa*=ff; } int main(){ cin>>T; while(T--){ bool p=0; read(n),read(a),read(b); if(b==1){ printf("Yes\n"); continue; } if(a==1){ if((n-1)%b==0) printf("Yes\n"); else printf("No\n"); continue; } for(ll i=1;i<=n;i*=a){ if((n-i)%b==0){ printf("Yes\n"); p=1;break; } } if(!p){ printf("No\n"); } } return 0; }
2.Codeforces Round #724 (Div. 2) C. Diluc and Kaeya


大意:给定DK序列的所有前缀中,对于每个前缀可以分为k段,使得分为的k段长度相同,且每段中D与K数量之比相同,求对于每个前缀这个k的最大值。
题解:将D出现的次数记为x,K出现的次数记为y,用(x,y)表示每个前缀,可得到坐标系中的n个点。其中,第 i 个点与原点相连穿过第 1~i 个点的数量就为答案。

#include<cmath> #include<cstdio> #include<cstdlib> #include<iostream> #include<cstring> #include<algorithm> #include<map> using namespace std; #define ll long long const int maxn=5e5+5; int T,n; char a; int gcd(int a,int b){ int c; while(a%b){ c=a%b; a=b; b=c; } return b; } template<typename T>void inline read(T &aa){ ll ff=1;char cc=getchar();aa=0; while((cc<'0'||cc>'9')&&cc!='-') cc=getchar(); if(cc=='-') ff=-1,cc=getchar(); while(cc<='9'&&cc>='0') aa=aa*10+cc-48,cc=getchar(); aa*=ff; } int main(){ cin>>T; while(T--){ map<pair<int,int>,int > mp; int sum1=0,sum2=0; cin>>n; for(int i=1;i<=n;i++){ cin>>a; if(a=='D') sum1++; else sum2++; pair<int,int> c; // cout<<sum1<<" "<<sum2<<endl; if(sum1==0){ c.first=0;c.second=0; } else if(sum2==0){ c.first=1;c.second=0; } else{ int g=gcd(sum1,sum2); // cout<<g<<endl; int x1=sum1/g,x2=sum2/g; c.first=x1;c.second=x2; } mp[c]++; cout<<mp[c]<<" "; } cout<<endl; } return 0; }
3.Codeforces Round #645 (Div. 2) Celex Update


大意:每次只能向下或者向右走,问两点间经过数字之和不同的路径有多少条?
题解:起点为(x1,y1),终点为(x2,y2),则答案为(x2-x1)*(y2-y1)+1 。
4.Codeforces Round #645 (Div. 2) D. The Best Vacation


大意:一年有n个月,第 i 个月有 d[i] 天,而每个月的第 k 天可以获得 k 点拥抱。你要旅游连续 x 天,问可以获得拥抱的最大值为多少?
题解:贪心可以发现,获得最大值时,旅游总是在某个月的最后一天结束。枚举每个月,假定这个月的最后一天结束,向前二分找到开始的月份,统计答案,取max。

#include<cmath> #include<cstdio> #include<cstdlib> #include<iostream> #include<cstring> #include<algorithm> using namespace std; #define ll long long const int maxn=4e5+50; ll n,x,d[maxn]; ll Sum[maxn],tot[maxn]; int find(int k,int l,int r){ if(l==r) return l; int m=l+r>>1; if(Sum[k]-Sum[m]<x) return find(k,l,m); return find(k,m+1,r); } template<typename T>void inline read(T &aa){ ll ff=1;char cc=getchar();aa=0; while((cc<'0'||cc>'9')&&cc!='-') cc=getchar(); if(cc=='-') ff=-1,cc=getchar(); while(cc<='9'&&cc>='0') aa=aa*10+cc-48,cc=getchar(); aa*=ff; } int main(){ cin>>n>>x; ll sum=0,Max=0; for(int i=1;i<=n;i++){ read(d[i]); d[i+n]=d[i]; } for(int i=1;i<=2*n;i++){ Sum[i]=Sum[i-1]+d[i]; tot[i]=tot[i-1]+(d[i]+1)*d[i]/2; } for(int i=1;i<=2*n;i++){ if(Sum[i]<x) continue; int y=find(i,1,i); ll num=x-Sum[i]+Sum[y]; Max=max(Max,tot[i]-tot[y]+(d[y]*2+1-num)*num/2); } cout<<Max<<endl; return 0; }
5.Codeforces Round #722 (Div. 2) C. Parsa's Humongous Tree

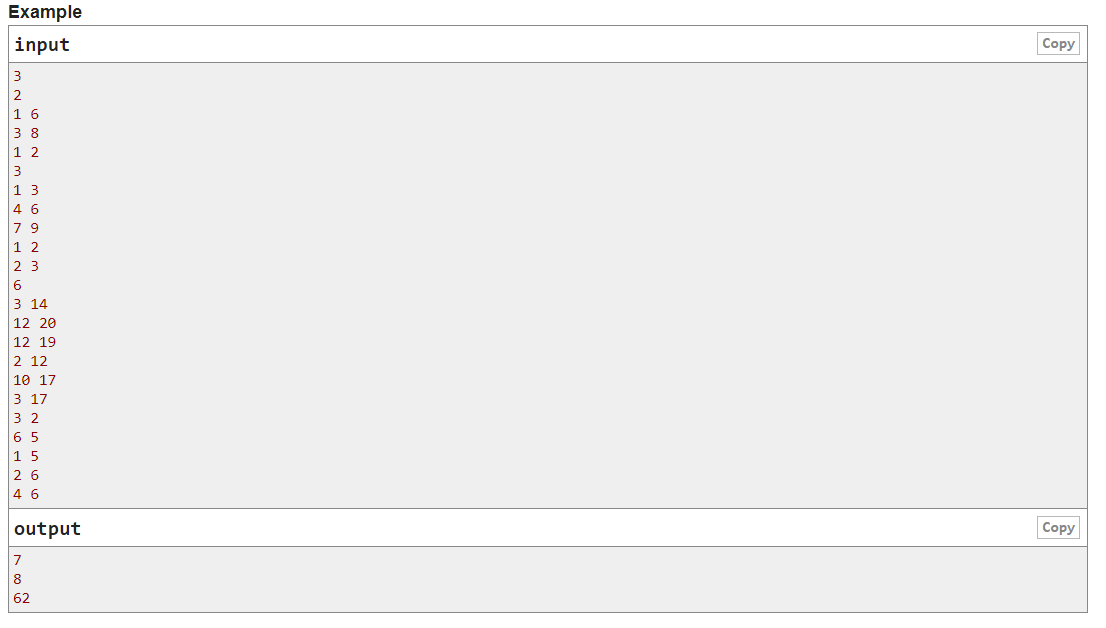
大意:一棵树的每个节点有两个值 l [ i ] 和 r [ i ] ,这个节点的权值为 a[ i ],a要满足 l [i] <= a [i] <= r [i] ,一条路径的值为路径两点的权值之差的绝对值,求所有路径的值之和的最大值。
题解:dp[ i ][ 0 ] 和 dp[ i ][ 1 ] 分别表示 i 节点取左、右值时其子树路径之和的最大值,设 v 是 i 的子节点,则有
dp[ i ][ 0 ] += max( dp[ v ][ 0 ] + abs( l[ i ] - l[ v ] ) , dp[ v ][ 1 ] + abs( l[ i ] - r[ v ] ) )
dp[ i ][ 1 ] += max( dp[ v ][ 0 ] + abs( r[ i ] - l[ v ] ) , dp[ v ][ 1 ] + abs( r[ i ] - r[ v ] ) )

#include<cmath> #include<cstdio> #include<cstdlib> #include<iostream> #include<cstring> #include<algorithm> using namespace std; #define ll long long const int maxn=2e5+50; const int maxm=4e5+50; int T,n,l[maxn],r[maxn]; int fir[maxn],nex[maxm],to[maxm],ecnt; ll dp[maxn][2]; void add(int u,int v){ nex[++ecnt]=fir[u];fir[u]=ecnt;to[ecnt]=v; } void dfs(int x,int f){ dp[x][0]=dp[x][1]=0; for(int e=fir[x];e;e=nex[e]){ int v=to[e]; if(v==f) continue; dfs(v,x); dp[x][0]+=max(dp[v][0]+abs(l[x]-l[v]),dp[v][1]+abs(l[x]-r[v])); dp[x][1]+=max(dp[v][0]+abs(r[x]-l[v]),dp[v][1]+abs(r[x]-r[v])); } } template<typename T>void inline read(T &aa){ ll ff=1;char cc=getchar();aa=0; while((cc<'0'||cc>'9')&&cc!='-') cc=getchar(); if(cc=='-') ff=-1,cc=getchar(); while(cc<='9'&&cc>='0') aa=aa*10+cc-48,cc=getchar(); aa*=ff; } int main(){ cin>>T; while(T--){ memset(fir,0,sizeof(fir)); memset(nex,0,sizeof(nex)); memset(to,0,sizeof(to)); ecnt=0; cin>>n; for(int i=1;i<=n;i++){ read(l[i]),read(r[i]); } int x,y; for(int i=1;i<n;i++){ read(x),read(y); add(x,y);add(y,x) ; } dfs(1,0); cout<<max(dp[1][0],dp[1][1])<<endl; } return 0; }
6.Codeforces Round #264 (Div. 2) D. Gargari and Permutations

大意:求 k 个 n 的全排列的最长公共子序列
题解:(1)可以将 k 个序列中均满足 i 出现在 j 的前面的 i 与 j 连边,求最长路
(2) 设dp[ i ] 为在第一个序列中到 i 能与所有序列形成的最长公共子序列长度,则往 i 后面枚举 j ,如果 a[ j ] 在其他序列中出现的位置均在 a[ i ] 后面,则 dp[ j ] = max( dp[ j ] , dp[ i ] +1 )。
最后将 dp[ i ] 取 max

#include<cmath> #include<cstdio> #include<cstdlib> #include<iostream> #include<cstring> #include<algorithm> using namespace std; #define ll long long const int maxn=1000+50; const int maxm=1e6+5; int n,k,a[6][maxn],id[6][maxn],dp[maxn]; template<typename T>void inline read(T &aa){ ll ff=1;char cc=getchar();aa=0; while((cc<'0'||cc>'9')&&cc!='-') cc=getchar(); if(cc=='-') ff=-1,cc=getchar(); while(cc<='9'&&cc>='0') aa=aa*10+cc-48,cc=getchar(); aa*=ff; } int main(){ cin>>n>>k; for(int i=1;i<=k;i++){ for(int j=1;j<=n;j++){ read(a[i][j]); id[i][a[i][j]]=j; } } for(int i=1;i<=n;i++) dp[i]=1; for(int i=1;i<=n;i++) for(int j=i+1;j<=n;j++){ bool p=0; for(int t=2;t<=k;t++){ if(id[t][a[1][j]]<=id[t][a[1][i]]){ p=1;break; } } if(p) continue; dp[j]=max(dp[j],dp[i]+1); } int ans=0; for(int i=1;i<=n;i++) ans=max(ans,dp[i]); cout<<ans; return 0; }
7.Codeforces Round #486 (Div. 3) D. Points and Powers of Two
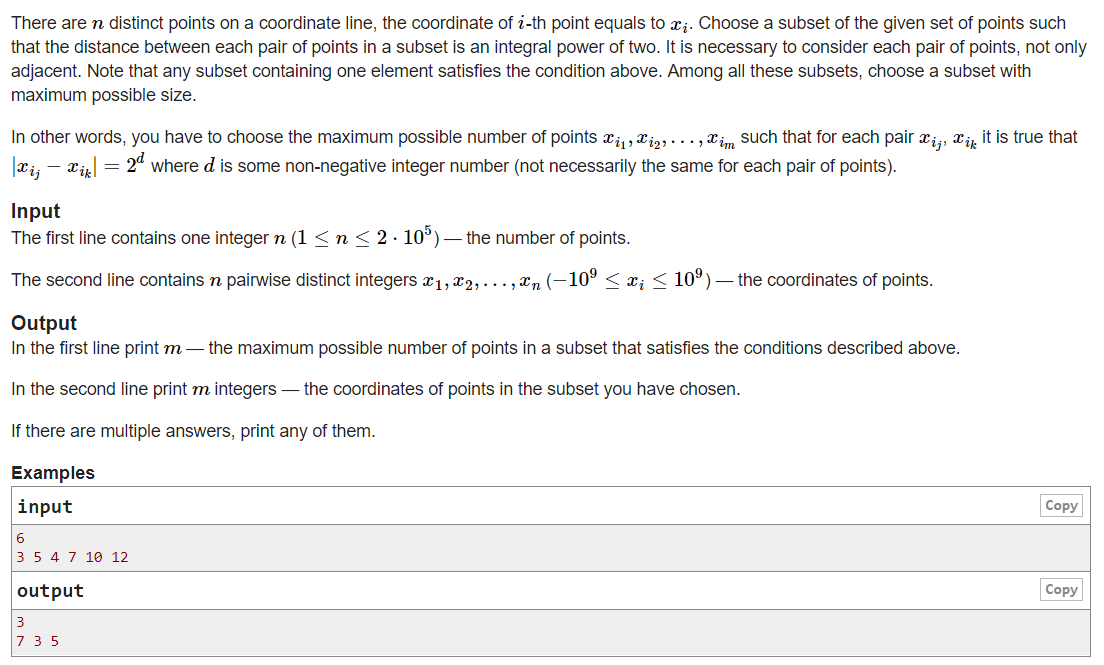
大意:给定n个数,找出最多的数,使他们任意两个数之差的绝对值为二的整次幂
题解:可以证明,最多只能找出3个数。枚举大小为中间的数为a,枚举2的次幂 k,查找 a-k 与 a+k 是否存在,存在则答案为3。若不存在继续判断答案为 2 的情况即可。

#include<cmath> #include<cstdio> #include<cstdlib> #include<iostream> #include<cstring> #include<algorithm> using namespace std; #define ll long long const int maxn=2e5+50; ll n,a[maxn],br,t=1,ans; ll er[100]; bool find(ll x,int l,int r){ if(l==r){ if(a[l]!=x) return false; return true; } int m=l+r>>1; if(a[m]<x) return find(x,m+1,r); if(a[m]>x) return find(x,l,m); if(a[m]==x) return true; } bool pd(int x){ for(int i=0;i<=t;i++) if(x%er[i]==0) return true; return false; } template<typename T>void inline read(T &aa){ ll ff=1;char cc=getchar();aa=0; while((cc<'0'||cc>'9')&&cc!='-') cc=getchar(); if(cc=='-') ff=-1,cc=getchar(); while(cc<='9'&&cc>='0') aa=aa*10+cc-48,cc=getchar(); aa*=ff; } int main(){ cin>>n; er[0]=1; for(int i=1;;t++,i++){ er[i]=er[i-1]*2; if(er[i]>2e9) break; } for(int i=1;i<=n;i++) read(a[i]); sort(a+1,a+1+n); if(n==1){ ans=1; cout<<ans<<endl<<a[1]; return 0; } if(n==2){ if(pd(a[2]-a[1])){ ans=2; cout<<ans<<endl<<a[1]<<" "<<a[2]; return 0; } else{ ans=1; cout<<ans<<endl<<a[1]<<" ";return 0; } } for(int i=2;i<n;i++){ for(int j=0;j<=t;j++){ ll x=a[i]-er[j],y=a[i]+er[j]; if(find(x,1,i-1)&&find(y,i+1,n)){ ans=3; cout<<ans<<endl<<x<<" "<<a[i]<<" "<<y;return 0; } } } for(int i=1;i<n;i++){ for(int j=1;j<=t;j++){ ll x=a[i]+er[j]; if(find(x,i+1,n)){ ans=2; cout<<ans<<endl<<a[i]<<" "<<x; return 0; } } } ans=1; cout<<ans<<endl<<a[1]; return 0; }
8.Codeforces Round #731 (Div. 3) E. Air Conditioners


大意:有n个点,k个空调,给出每个空调的位置a[ i ]和温度 t[ i ],对于一个点 i ,它的温度为![]() ,求每个点的温度
,求每个点的温度
题解:设L[ i ] 表示点 i 以及 i 左边的点对 i 的贡献,即 i 点有空调时 L[ i ] = min ( L[ i-1 ] +1 , t[ i ] ) , 否则 L [ i ] = L[ i-1 ] + 1
同样,设R[ i ] 表示点 i 以及 i 右边的点对 i 的贡献,即 i 点有空调时 R[ i ] = min ( R[ i+1 ] +1, t[ i ] ), 否则 R [ i ] = R[ i+1 ] + 1
最后 i 点的答案就为 min( L[ i ] , R[ i ] )

#include<cmath> #include<cstdio> #include<cstdlib> #include<iostream> #include<cstring> #include<algorithm> using namespace std; #define ll long long const int maxn=3e5+50; const int maxx=2e9; ll L[maxn],R[maxn],T[maxn]; int TT,n,k; bool P[maxn]; struct node{ int p; ll t; }a[maxn]; int cmp(const node &a,const node &b){ return a.p<b.p; } template<typename T>void inline read(T &aa){ ll ff=1;char cc=getchar();aa=0; while((cc<'0'||cc>'9')&&cc!='-') cc=getchar(); if(cc=='-') ff=-1,cc=getchar(); while(cc<='9'&&cc>='0') aa=aa*10+cc-48,cc=getchar(); aa*=ff; } int main(){ cin>>TT; while(TT--){ cin>>n>>k; memset(P,0,sizeof(P)); for(int i=1;i<=k;i++){ read(a[i].p); P[a[i].p]=true; } for(int i=1;i<=k;i++) read(a[i].t); for(int i=1;i<=k;i++) T[a[i].p]=a[i].t; for(int i=0;i<=n+1;i++) L[i]=maxx,R[i]=maxx; sort(a+1,a+1+k,cmp); for(int i=a[1].p;i<=n;i++){ if(P[i]) L[i]=min(L[i-1]+1,T[i]); else L[i]=L[i-1]+1; } for(int i=a[k].p;i>=1;i--){ if(P[i]) R[i]=min(R[i+1]+1,T[i]); else R[i]=R[i+1]+1; } for(int i=1;i<=n;i++) cout<<min(L[i],R[i])<<" "; cout<<endl; } return 0; }
9.Codeforces Round #732 (Div. 2) B. AquaMoon and Stolen String


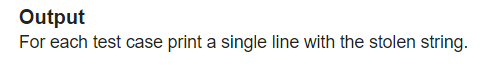
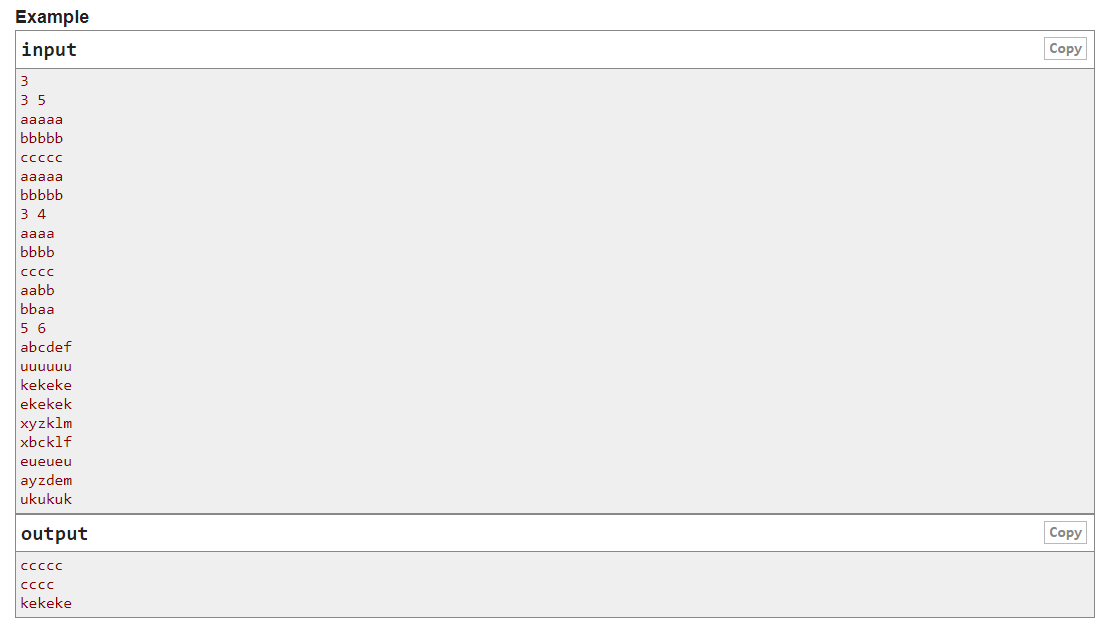
大意:有奇数n个字符串,将其中n-1个两两配对,一对字符串中相同位置可以交换,如aaaa与bbbb可以交换为aabb与bbaa,给出这n-1个交换后的串,求剩下的那一个串
题解:注意 a^b^b = a , 对于输入的 2*n-1 个串,对他们的位置 i 进行异或,得到的答案就是剩下的那个串的位置 i 。

#include<cmath> #include<cstdio> #include<cstdlib> #include<iostream> #include<cstring> #include<algorithm> using namespace std; #define ll long long const int maxn=2e5+50; int T,n,m; string a[maxn]; int main(){ cin>>T; while(T--){ cin>>n>>m; for(int i=1;i<=2*n-1;i++) cin>>a[i]; for(int i=0;i<m;i++){ int cur=0; for(int j=1;j<=2*n-1;j++) cur^=(a[j][i]-'a'); cout<<char(cur+'a'); } cout<<endl; } return 0; }
10.Codeforces Round #732 (Div. 2)C. AquaMoon and Strange Sort
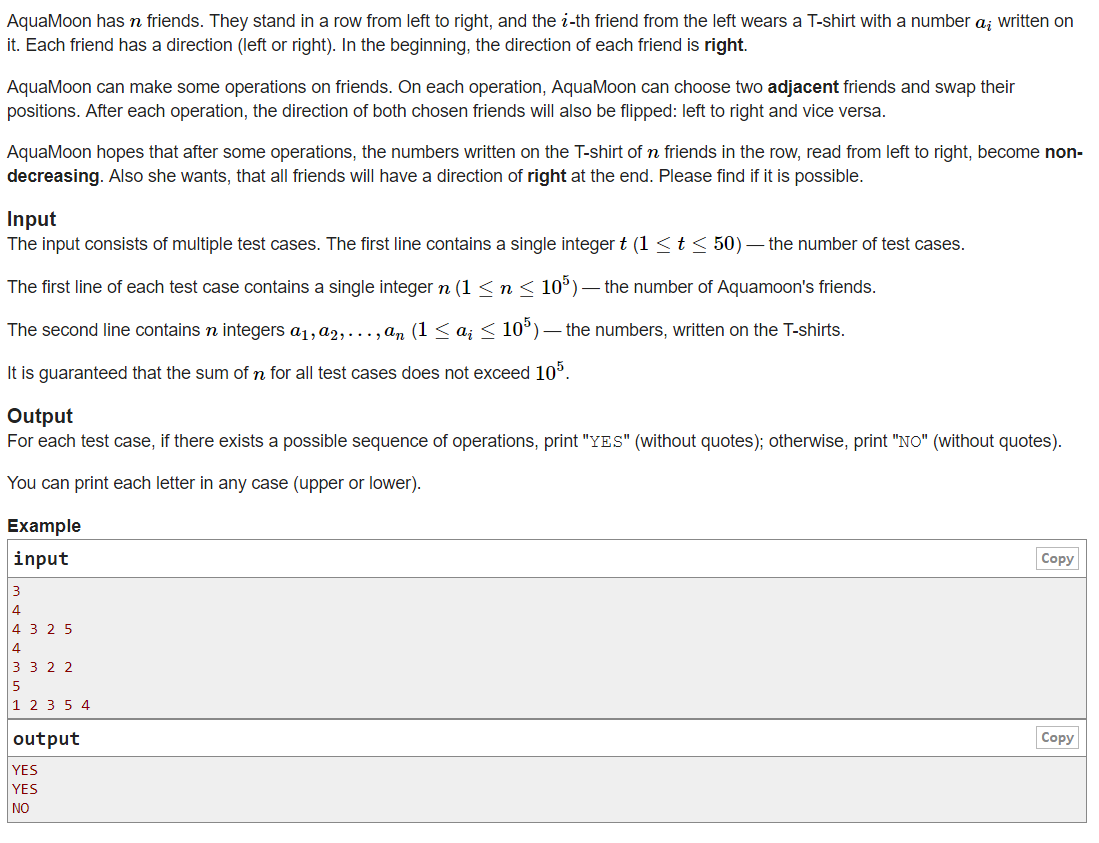

大意:有n个数,他们的方向开始都朝右,每次操作可以将一个数与它相邻的数交换,同时这两个数的方向改变,问能不能使得这n个数不降排列且每个数的方向都向右?
题解:方向不变,则每个数都要交换偶数次。记录原数列中每个数出现的奇数位置、偶数位置的次数,再将数列排序,若排序后的数列中每个数出现在奇数、偶数位置的次数与原数列不同,则不满足;否则满足。

#include<cmath> #include<cstdio> #include<cstdlib> #include<iostream> #include<cstring> #include<algorithm> using namespace std; #define ll long long const int maxn=1e5+50; int T,n,a[maxn],odd[maxn],even[maxn]; template<typename T>void inline read(T &aa){ ll ff=1;char cc=getchar();aa=0; while((cc<'0'||cc>'9')&&cc!='-') cc=getchar(); if(cc=='-') ff=-1,cc=getchar(); while(cc<='9'&&cc>='0') aa=aa*10+cc-48,cc=getchar(); aa*=ff; } int main(){ cin>>T; while(T--){ memset(odd,0,sizeof(odd)); memset(even,0,sizeof(even)); cin>>n; for(int i=1;i<=n;i++){ read(a[i]); if(i%2) odd[a[i]]++; else even[a[i]]++; } sort(a+1,a+1+n); for(int i=1;i<=n;i++){ if(i%2) odd[a[i]]--; else even[a[i]]--; } bool p=0; for(int i=1;i<=1e5;i++){ if(even[i]!=0||odd[i]!=0){ p=1;break; } } if(p){ cout<<"NO"<<endl; } else cout<<"YES"<<endl; } return 0; }
11.The 2020 ICPC Asia Macau Regional Contest F. Fixing Networks

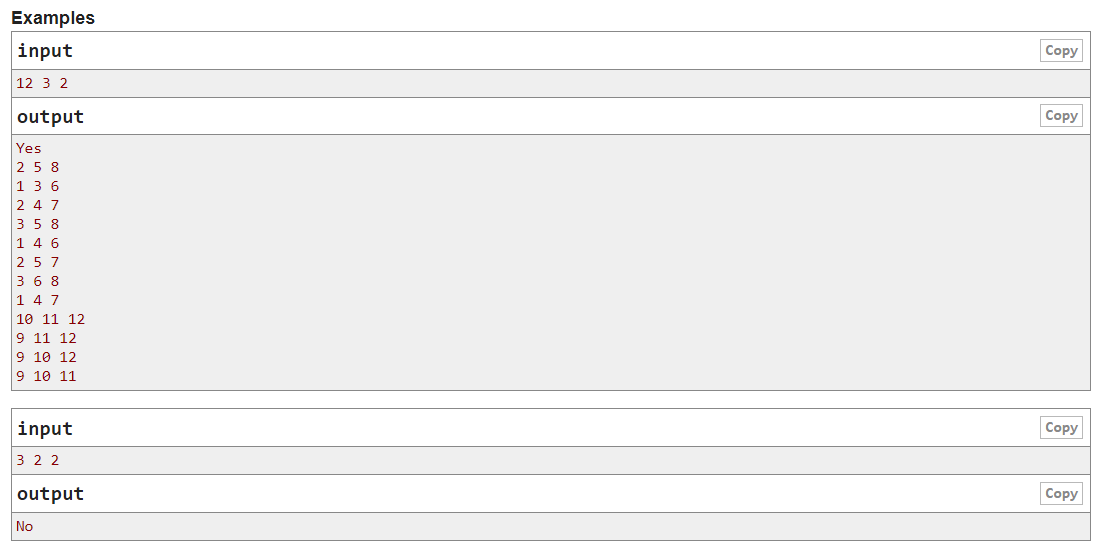
大意:有n个点,要求每个点恰好与d个点相连,且这n个点分为c块,块内各点连通,块与块之间不连通,能否构造?
题解:每个点需要连接d个点,则一块至少需要d+1个点,即( d+1 )*c 需要小于等于n,同时,n和d不能都为奇数。单独判断d=0和d=1,对于其他情况,取d+1个点为一个块,这个块内的点两两相连,可以构造
c-1个这样的块。对于剩下的m个点,它们需要构成一块,取 k=d/2 (向下取整),这m个点每个点向其前后k个点分别连边,若d为奇数,此时m必然为偶数,则再将每个点与其对称点连边即可。

#include<cmath> #include<cstdio> #include<cstdlib> #include<iostream> #include<cstring> #include<algorithm> using namespace std; #define ll long long ll n,d,c,ans[100000+50],t; template<typename T>void inline read(T &aa){ ll ff=1;char cc=getchar();aa=0; while((cc<'0'||cc>'9')&&cc!='-') cc=getchar(); if(cc=='-') ff=-1,cc=getchar(); while(cc<='9'&&cc>='0') aa=aa*10+cc-48,cc=getchar(); aa*=ff; } int main(){ cin>>n>>d>>c; if((d+1)*c>n||(n%2&&d%2)){ cout<<"No"<<endl; return 0; } if(d==0){ if(n==c){ cout<<"Yes"<<endl; } else{ cout<<"No"<<endl; } return 0; } if(d==1){ if(n==2*c){ cout<<"Yes"<<endl; for(int i=1;i<=n;i++){ if(i%2) cout<<i+1<<endl; else cout<<i-1<<endl; } } else{ cout<<"No"<<endl; } return 0; } cout<<"Yes"<<endl; for(int i=1;i<=(c-1)*(d+1);i++){ ll id=(i-1)/(d+1),st=id*(d+1)+1,ed=(id+1)*(d+1); for(int j=st;j<=ed;j++){ if(j==i) continue; cout<<j<<" "; } cout<<endl; } ll k=d/2,sum=n-(c-1)*(d+1),st=(c-1)*(d+1)+1; for(int i=st;i<=n;i++){ t=0; for(int j=i+1;j<=i+k;j++){ if(j>n) ans[++t]=j-sum; else if(j<st) ans[++t]=j+sum; else ans[++t]=j; } if(d%2){ int x=i+sum/2; if(x>n) x-=sum; ans[++t]=x; } for(int j=i-k;j<=i-1;j++){ if(j>n) ans[++t]=j-sum; else if(j<st) ans[++t]=j+sum; else ans[++t]=j; } sort(ans+1,ans+1+t); for(int i=1;i<=t;i++) cout<<ans[i]<<" "; cout<<endl; } return 0; }
12.The 2020 ICPC Asia Macau Regional Contest G. Game on Sequence

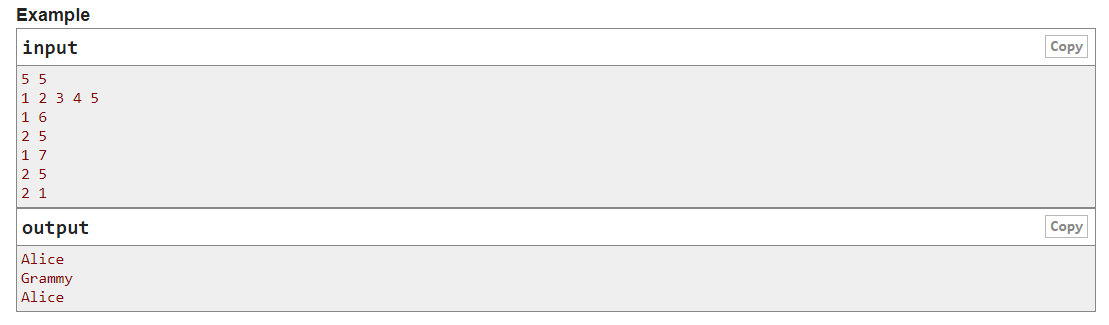
大意:有一个长度为n的序列,Grammy和Alice在这个序列上玩一个游戏,他们从位置k开始,Grammy先进行,每次他们需要从当前数向后跳,且要满足跳到的数与当前数在二进制表示上最多一位不同,最后不能跳的人输掉游戏。现在有m个操作,操作 1 k 表示在这个序列的最后面加上一个数 k ,操作 2 k 表示游戏从位置 k 开始,输出谁能赢下这个游戏。
题解:对于两个位置 i,j ( i<j ) 并且 a[ i ] = a[ j ] ,若 a[ j ]必败,由于a[ i ]可以跳到 a[ j ],则a[ i ]必胜;若a[ j ] 必胜,表示a[ j ]可以跳到后面一个必败的点,则a[ i ]同样可以跳到那个点,a[ i ]必胜。可以看出,如果一个数后面有与它相同的数,则这个数必胜。所以只需要判断一个数最后出现的位置能不能必胜。从后向前推,若当前数可以跳到的数中,有必败的数,则当前数必胜,否则当前数必败。

#include<bits/stdc++.h> using namespace std; #define ll long long const int maxn=4e5+50; int n,m,a[maxn],loc[maxn]; bool f[maxn]; int cmp(int x,int y){ return loc[x]>loc[y]; } template<typename T>void inline read(T &aa){ ll ff=1;char cc=getchar();aa=0; while((cc<'0'||cc>'9')&&cc!='-') cc=getchar(); if(cc=='-') ff=-1,cc=getchar(); while(cc<='9'&&cc>='0') aa=aa*10+cc-48,cc=getchar(); aa*=ff; } void work(){ int lim=256; memset(f,1,sizeof(f)); vector<int> v; for(int i=0;i<lim;i++){ if(loc[i]) v.push_back(i); } sort(v.begin(),v.end(),cmp); for(int i=0;i<v.size();i++){ bool p=0; int x=v[i]; for(int k=0;k<8;k++) if(!f[x^(1<<k)]) p=1; if(p) f[x]=1; else f[x]=0; } } int main(){ cin>>n>>m; for(int i=1;i<=n;i++){ read(a[i]); loc[a[i]]=i; } work(); int op,k; while(m--){ cin>>op>>k; if(op==1){ a[++n]=k; loc[k]=n; work(); } else{ if(loc[a[k]]==k){ if(f[a[k]]) cout<<"Grammy"<<endl; else cout<<"Alice"<<endl; } else cout<<"Grammy"<<endl; } } return 0; }
13.Codeforces Round #721 (Div. 2) C. Sequence Pair Weight
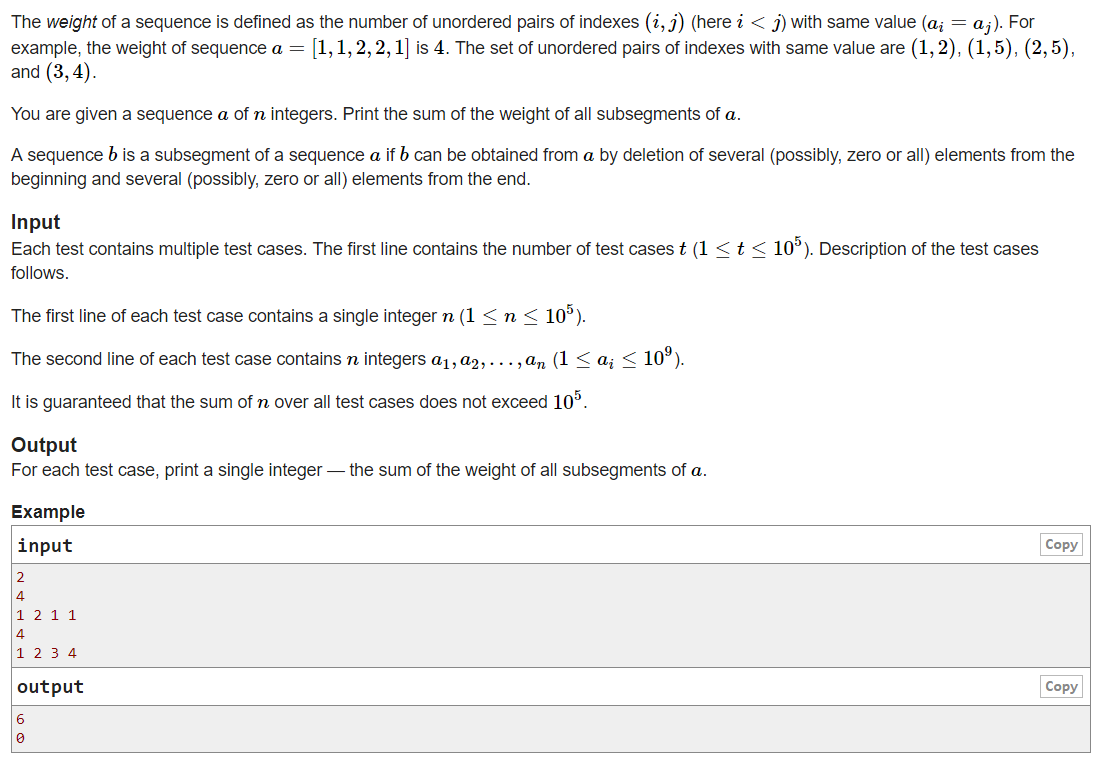

大意:一个序列中,一对相同元素可以提供一重量,给定一个n个数的序列,求这个序列的所以子串 ( 包括自己且要求连续 )的重量的和。
题解:设dp[ i ]为以第 i 位结束的所有串的重量和,则答案为dp[ 1 ] + dp[ 2 ] +...+ dp[ n ]。对于第 i 位,如果在第 j 位 ( j < i )的数a[ j ] = a[ i ],则它的贡献为 j ,所以 dp[ i ] = dp[ i-1 ] + ∑ j ( j < i,且a[ j ] = a[ i ] )

#include<bits/stdc++.h> using namespace std; #define ll long long const int maxn=1e5+50; ll T,n,a[maxn]; ll dp[maxn]; map<ll,ll> mp; template<typename T>void inline read(T &aa){ ll ff=1;char cc=getchar();aa=0; while((cc<'0'||cc>'9')&&cc!='-') cc=getchar(); if(cc=='-') ff=-1,cc=getchar(); while(cc<='9'&&cc>='0') aa=aa*10+cc-48,cc=getchar(); aa*=ff; } int main(){ cin>>T; while(T--){ mp.clear(); read(n);dp[0]=0; ll ans=0; for(int i=1;i<=n;i++){ read(a[i]); mp[a[i-1]]+=i-1; dp[i]=dp[i-1]+mp[a[i]]; ans+=dp[i]; } cout<<ans<<endl; } return 0; }
14.Codeforces Round #683 (Div. 2, by Meet IT) D. Catching Cheaters


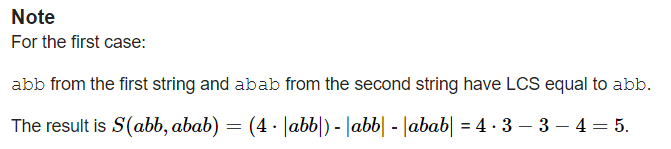
大意:给你两个字符串A和B,C和D分别为A和B的子串,定义S(C,D) = 4*LCS(C,D) - |C| - |D| ,其中 LCS(C,D) 表示C和D的最长公共子序列,对于A和B的任意子串C和D,求出S(C,D) 的最大值。
题解:设dp[ i ][ j ] 为以a[ i ] 结尾,b[ j ]结尾的两个串的最大S值,枚举 i,j,如果a[ i ] = b[ j ],则 LCS增加1,S值增加2,有dp[ i ][ j ]=max( dp[ i ][ j ], dp[ i-1 ][ j-1 ] + 2 );如果 a[ i ] ≠ b[ j ],则 dp[ i ][ j ] = max( dp[ i ][ j ],dp[ i ][ j-1 ] -1 ) ,dp[ i ][ j ] = max( dp[ i ][ j ],dp[ i-1 ][ j ] -1 )。最后对每个dp[ i ][ j ] 取max得到答案。

#include<cmath> #include<cstdio> #include<cstdlib> #include<iostream> #include<cstring> #include<algorithm> using namespace std; #define ll long long const int maxn=5050; int n,m,dp[maxn][maxn],ans; char a[maxn],b[maxn]; template<typename T>void inline read(T &aa){ ll ff=1;char cc=getchar();aa=0; while((cc<'0'||cc>'9')&&cc!='-') cc=getchar(); if(cc=='-') ff=-1,cc=getchar(); while(cc<='9'&&cc>='0') aa=aa*10+cc-48,cc=getchar(); aa*=ff; } int main(){ cin>>n>>m; cin>>a+1; cin>>b+1; for(int i=1;i<=n;i++) for(int j=1;j<=m;j++){ if(a[i]==b[j]) dp[i][j]=dp[i-1][j-1]+2; else{ dp[i][j]=max(dp[i][j],dp[i-1][j]-1); dp[i][j]=max(dp[i][j],dp[i][j-1]-1); } ans=max(ans,dp[i][j]); } cout<<ans<<endl; return 0; }
15.The 15th Heilongjiang Provincial Collegiate Programming Contest C. Cornelia Street
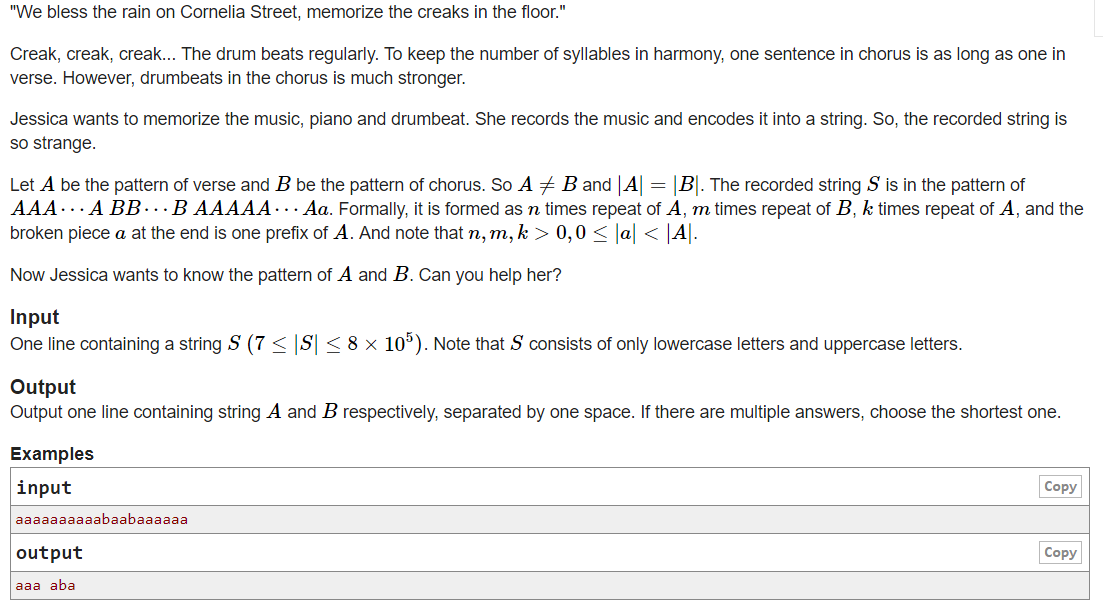
大意:一个字符串S由 AA....ABBB...BAA..Aa 组成,其中A与B的长度相同,但数量不一定相同,a是A的一个前缀,求最短的A,B。
题解:先求出整个串的hash值,枚举所求长度,算出每段的hash值,若除开A的前缀a之外只有两种hash值,则满足要求。

#include<cmath> #include<cstdio> #include<cstdlib> #include<iostream> #include<cstring> #include<algorithm> using namespace std; #define ll long long const int maxn=8e5+50; const ll base=131; const ll mod=1e9+7; char a[maxn]; ll hhash[maxn],ans,mul[maxn]; int main(){ cin>>a+1; int len=strlen(a+1);mul[0]=1; for(int i=1;i<=len;i++) hhash[i]=(hhash[i-1]*base+(ll)a[i])%mod,mul[i]=mul[i-1]*base%mod; int id; for(int l=1;l<=len/2;l++){ int tot=0;ll sum=0,pre; bool p=0; for(int i=l;i<=len;i+=l){ ll pp=hhash[i]-mul[l]*hhash[i-l]%mod; if(pp<0) pp+=mod; if(sum!=pp){ if(sum==0) pre=pp; if(tot==1) id=i-l+1; sum=pp; tot++; if(tot>=3){ if(tot==3&&sum==pre) continue; p=1;break; } } } if(p) continue; int las=len%l; if((hhash[len]-mul[las]*hhash[len-las]%mod+mod)%mod==hhash[las]){ ans=l; break; } } // cout<<ans<<endl; for(int i=1;i<=ans;i++) cout<<a[i]; cout<<" "; for(int i=id;i<=id+ans-1;i++) cout<<a[i]; return 0; }
2021.7.16


