P3581 [POI2015] CZA 题解
思路：
找性质 dp。
我们首先观察，\(p \le 1\) 显然除非 \(n=1\) 否则无解，\(p=2\) 的话只能把奇数和偶数分别放在一起，只有两种情况。
所以最难的是 \(p=3\) 的情况。
我们发现，整个环大致是这样的：从 \(1\) 出发两条不相交的路径，经过一些点，然后在 \(n\) 汇合。
而且我们注意到，由于 \(p\) 很小，这两个序列是大致单调的。
更具体，如果连续三个数都在同一路径上，那么显然是无解的。
所以我们可以考虑 dp。设 \(f(i,j)\) 表示上面走到 \(i\)，下面走到 \(j\) 的方案数。
但是这样有可能重复，所以我们钦定 \(i < j\) 且 \(i\) 的下一个 \(> j\)。
我们发现只存在三种情况：\(j = i + 1\)，\(j = i + 2\) 且 \(i+1\) 是否填完。
于是开始快乐的分类讨论。
对于 \(j = i + 1\) 的转移，我们按照 \(i\) 的下一个是谁讨论。
如果 \(i\) 的下一个是 \(i + 2\)，则有这样的情况：
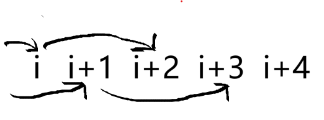
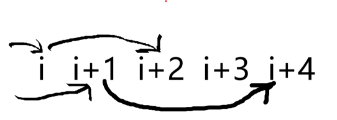
一定要注意我们的条件，下一个要 $ > j$.
如果下一个是 \(i+3\)，则有这样的情况：
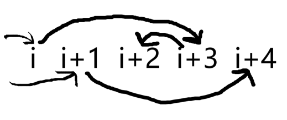
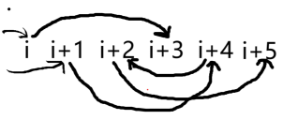
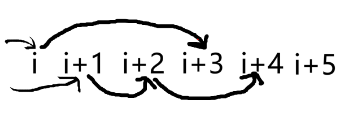
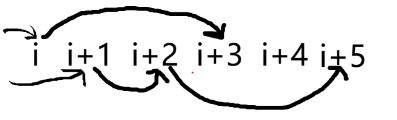
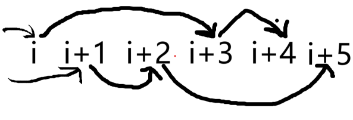
这样这一种全部转移完了。
我们考虑 \(i+1\) 没有用掉的情况，有以下几种：
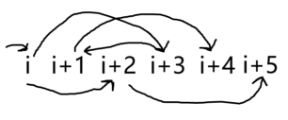
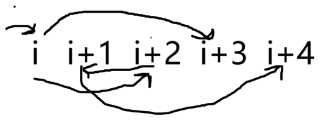
如果 \(i+1\) 被用掉，有：
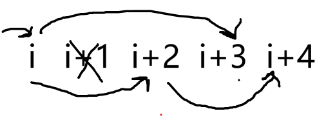
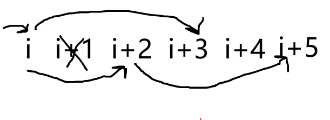
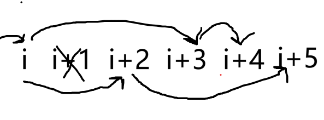
现在我们已经转移完了，但是我们还需要考虑两个事儿：初始和统计答案。
对于初始，我们都是从 \(1\) 出发，我们枚举下方第一条边的情况：
如果是 2：
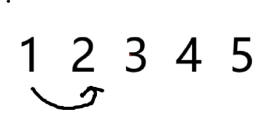
如果是 3：
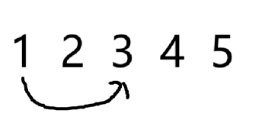
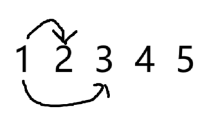
如果是 4：
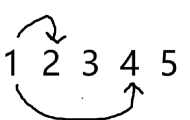
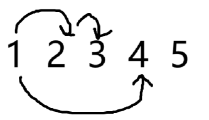
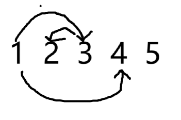
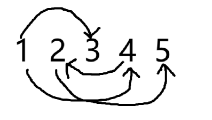
这样初始就解决了。
现在考虑统计答案，我们枚举 \(i\) 的状态即可：
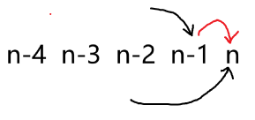
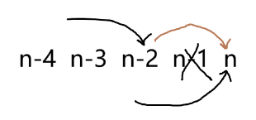
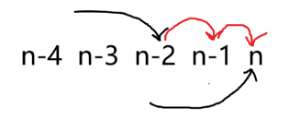
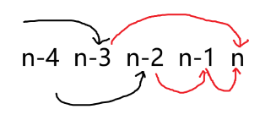
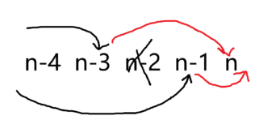
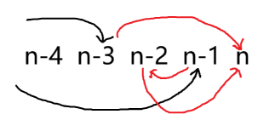
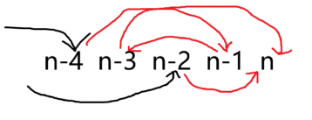
这样就完成了所有讨论，时间复杂度 \(O(n)\)。
点击查看代码
#include <iostream>
#include <cstdio>
#include <vector>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1e6 + 5;
const int M = 1e5 + 5;
const int mod = 1e9 + 7;
void add(int &x, int y) {
x = (x + y) % mod;
}
int n = 0, m, p;
bool mtr[N][7] = {{0}};//表示 mtr[i][j] 表示 i + 3 - j 能否坐在右边
bool chk(int x, int y) {//y 坐在 x 右边
return !mtr[x][y - x + 3] && x <= n && y <= n;
}
bool chk2(int x, int y) {
return chk(y, x);
}
namespace SLV1 {
int f[N][3] = {{0}};
//f[i][0] 表示 (i, i + 1)
//f[i][1] 表示 (i, 0, i + 2)
//f[i][2] 表示 (i, x, i + 2)
void slv() {
// for (int x = 1; x <= n; x++) {
// for (int y = 1; y <= n; y++) {
// cout << x << " " << y << " " << chk(x, y) << endl;
// }
// }
//初始的转移
if (chk2(1, 2))
add(f[1][0], 1);
if (chk2(1, 3)) {
add(f[1][1], 1);
if (chk(1, 2))
add(f[2][0], 1);
}
if (chk2(1, 4)) {
if (chk(1, 2)) {
add(f[2][1], 1);
if (chk(2, 3))
add(f[3][0], 1);
}
if (chk(1, 3)) {
if (chk(3, 2))
add(f[2][2], 1);
if (chk2(4, 2) && chk2(2, 5))
add(f[3][2], 1);
}
}
for (int i = 1; i <= n; i++) {
//f[i][0] 的转移
if (chk(i, i + 2)) {
if (chk2(i + 1, i + 3))
add(f[i + 2][0], f[i][0]);
if (chk2(i + 1, i + 4)) {
add(f[i + 2][1], f[i][0]);
if (chk(i + 2, i + 3))
add(f[i + 3][0], f[i][0]);
}
}
if (chk(i, i + 3)) {
if (chk2(i + 1, i + 4) && chk(i + 3, i + 2))
add(f[i + 2][2], f[i][0]);
if (chk2(i + 1, i + 4) && chk2(i + 4, i + 2) && chk2(i + 2, i + 5))
add(f[i + 3][2], f[i][0]);
if (chk2(i + 1, i + 2) && chk2(i + 2, i + 4))
add(f[i + 3][0], f[i][0]);
if (chk2(i + 1, i + 2) && chk2(i + 2, i + 5)) {
add(f[i + 3][1], f[i][0]);
if (chk(i + 3, i + 4))
add(f[i + 4][0], f[i][0]);
}
}
//f[i][1] 的转移
if (chk(i, i + 3) && chk(i + 3, i + 1) && chk(i + 1, i + 4) && chk2(i + 2, i + 5))
add(f[i + 4][0], f[i][1]);
if (chk(i, i + 3) && chk2(i + 2, i + 1) && chk2(i + 1, i + 4))
add(f[i + 3][0], f[i][1]);
//f[i][2] 的转移
if (chk(i, i + 3) && chk2(i + 2, i + 4))
add(f[i + 3][0], f[i][2]);
if (chk(i, i + 3) && chk2(i + 2, i + 5)) {
add(f[i + 3][1], f[i][2]);
if (chk(i + 3, i + 4))
add(f[i + 4][0], f[i][2]);
}
// cout << i << " f[0]:" << f[i][0] << " f[1]:" << f[i][1] << " f[2]:" << f[i][2] << endl;
}
//统计答案
int ans = 0;
if (chk(n - 1, n))
add(ans, f[n - 1][0]);
if (chk(n - 2, n)) {
add(ans, f[n - 2][2]);
if (chk2(n - 1, n))
add(ans, f[n - 2][0]);
}
// cout << "look " << ans << endl;
if (chk(n - 3, n) && chk2(n - 2, n - 1) && chk(n - 1, n))
add(ans, f[n - 3][0]);
// cout << "look2 " << ans << endl;
if (chk(n - 3, n) && chk2(n - 1, n))
add(ans, f[n - 3][2]);
// cout << "look3 " << ans << endl;
if (chk(n - 3, n) && chk2(n - 1, n - 2) && chk2(n - 2, n))
add(ans, f[n - 3][1]);
if (chk(n - 4, n - 1) && chk(n - 1, n - 3) && chk(n - 3, n) && chk2(n - 2, n))
add(ans, f[n - 4][1]);
printf("%d\n", ans);
}
}
namespace SLV2 {
int t[N] = {0};
void slv() {
for (int i = 1; i < n; i++)
t[i] = i;
int ans = 0;
do {
bool flg = true;
t[n] = n;
for (int i = 1; i <= n; i++)
if (abs(t[i] - t[i % n + 1]) > p || !chk(t[i], t[i % n + 1]))
flg = false;
ans += flg;
// if (flg && t[5] == 4) {
// for (int i = 1; i <= n; i++)
// cout << t[i] << " ";
// cout << endl;
// }
} while (next_permutation(t + 1, t + n));
cout << ans << endl;
}
}
int ans[N] = {0};
int main() {
scanf("%d%d%d", &n, &m, &p);
for (int i = 1; i <= m; i++) {
int u, v;
scanf("%d%d", &u, &v);
if (abs(u - v) <= p)
mtr[u][v - u + 3] = true;
}
// for (int i = 1; i <= n; i++)
// for (int j = 1; j <= n; j++)
// cout << i << " " << j << " " << chk(i, j) << endl;
if (n <= 8) {
SLV2::slv();
return 0;
}
if (p == 0) {
if (n == 1)
printf("1\n");
else
printf("0\n");
return 0;
}
if (p == 1) {
if (n <= 2)
printf("1\n");
else
printf("0\n");
return 0;
}
if (p == 2) {
if (n == 2) {
if (chk(1, 2) && chk(2, 1)) {
cout << 1 << endl;
}
else
cout << 0 << endl;
return 0;
}
int cur = 1, len = 0;
while (cur <= n) {
ans[++len] = cur;
cur += 2;
}
cur = (cur == n + 1 ? n : n - 1);
while (cur > 1) {
ans[++len] = cur;
cur -= 2;
}
//for (int i = 1; i <= len; i++)
// cout << ans[i] << " ";
//cout << endl;
bool flg = true;
for (int i = 1; i <= len; i++)
if (!chk(ans[i], ans[i % n + 1]))
flg = false;
int tmp = flg;
flg = true;
for (int i = 1; i <= len; i++)
if (!chk2(ans[i], ans[i % n + 1]))
flg = false;
tmp += flg;
printf("%d\n", tmp);
return 0;
}
if (p == 3) {
SLV1::slv();
}
return 0;
}
