万能欧几里得小记
类欧几里得
类欧几里得算法解决这样的问题:
可以理解为一条直线下方的整点个数。
第一步
首先,我们可以将 \(r\) 对 \(q\) 取模,从而提取出一个不变量。
第二步
我们可以继续将 \(p\) 对 \(q\) 取模,从而使得 \(p,r\) 都在 \([0, q)\) 内。
第三步
现在会发现这条直线斜率和截距小于 \(1\),于是我们考虑通过对称和割补法使得又变成一条斜率大于 \(1\) 的直线,并且规模变小,从而达到辗转相除的效果。
好了现在你已经会了类欧几里得了。
但是由于这个东西有难推,而且形式一变就要重新推,所以不如学万能欧几里得。
万能欧几里得
还是考虑上面的求和,我们不妨考虑这样一个过程。
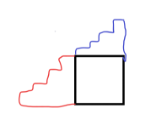
从原点出发,能往上走就往上走,不行就往右走,边走边统计答案,什么时候走出了 \(n\) 就得出答案。
不妨设 \(y(x) = [\frac{px+r}{q}]\)。
不妨用矩阵表示,我们维护 \(v = (y, ty = \sum y(x),1)\),则我们定义两个矩阵辅助转移:
\(U\):将 \((y, ty, 1) \to (y + 1, ty, 1)\)。
\(R\):将 \((y, ty, 1) \to (y, ty + y, 1)\)。
显然有这样的线性变换,所以我们现在只用将矩阵的乘积求出来就可以了。
不妨设:
其中定义 \(y(-1) = 0\)。
第一步
还是尝试 \(r\) 对 \(q\) 取模,设 \(r = r_0 + kq\),则考虑 \(y(x) - y(x-1)\) 的影响,发现除了第一项都可以抵消,所以我们得到:
第二步
尝试 \(p\) 对 \(q\) 取模,设 \(p = p_0 + kq\),则我们不难发现 \(y(x + 1) - y(x) \ge k\),这意味这我们可以尝试令 \(R' = U^kR\)。
考虑第一项 \(y(0) = [\frac{r}{q}]\),由于第一步所以 \(y(0) = 0\),于是我们得到:
现在在于找到合适的 \(y'(x)\),根据条件可以得到:
所以最终我们得到:
第三步
最关键的一步:如何辗转相除?
根据类欧的结论,我们现在是一条斜率截距均小于 1 的直线,这意味这 \(x\) 要比 \(y\) 多。
也就是最终的式子中,\(U\) 的个数更少,而我们现在是通过枚举 \(R\),来计算 \(U\)。所以我们现在通过枚举 \(U\) 然后计算 \(R\) 从而实现规模的减少。
不难发现,现在总共有 \(m = [\frac{pn+r}{q}]\) 个 \(U\),设 \(g(i)\) 表示第 \(i\) 个 \(U\) 的左边 \(R\) 的个数(其实所谓的 \(y(x)\) 和 \(g(i)\) 意义是相同的),则:
所以现在我们再去计算就会得到:
所以我们终于得到:
于是我们就完成了关键的三步。
时间复杂度
首先辗转相除的时间复杂度是 \(\log \max(p,q)\),但是我们算一些矩阵的乘法快速幂会不会导致复杂升高?
不会,因为每次都是类似 \(\log(\frac{p_1}{p_2})\) 的时间,将所有的对数展开可以一一抵消。
所以现在就是 \(O(T \log \max(p, q))\),其中 \(T\) 是矩阵乘法的常数。
更进一步
我们发现,矩阵只是一个幌子,只要像线段树一样满足结合律的运算都可以,所以我们其实写一个结构题并重新定义乘法即可。
万能欧几里得的本质是计算 \(UR\) 的成绩,这意味着我们可以随便定义 \(UR\),对于所有类似的问题都可以做,且代码主题保持不变。
练习题
P5170 【模板】类欧几里得算法
求 \(\sum y, \sum y^2, \sum xy\)。
重点在于思考这样的标记合成:
这道题记录当前的 \(x,y\),\(x,y\) 之和以及 \(y^2, xy\) 之和即可。
注意到我们是从原点出发,所以 \(U,R\) 都只有 \(x\) 或 \(y\) 是 \(1\)。
点击查看代码
#include <iostream>
#include <vector>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int mod = 998244353;
typedef long long ll;
struct Node {
ll x, y, sumx, sumy, sqry, prod;
Node (ll _x = 0, ll _y = 0, ll _sumx = 0, ll _sumy = 0, ll _sqry = 0, ll _prod = 0) :
x(_x), y(_y), sumx(_sumx), sumy(_sumy), sqry(_sqry), prod(_prod) {}
};
Node operator*(Node a, Node b) {
return Node((a.x + b.x) % mod, (a.y + b.y) % mod, (a.sumx + b.sumx + a.x * b.x) % mod, (a.sumy + b.sumy + a.y * b.x) % mod, (a.sqry + b.sqry + b.x * a.y % mod * a.y % mod + 2 * b.sumy * a.y % mod) % mod, (a.prod + b.prod + b.sumy * a.x % mod + a.y * b.sumx % mod + a.x * a.y % mod * b.x % mod) % mod);
}
Node fpow(Node a, ll b) {
if (b == 0)
return Node();
Node t = fpow(a, b / 2);
return (b % 2 == 1) ? t * t * a : t * t;
}
Node slv(ll p, ll q, ll r, ll n, Node U, Node R) {
if (r >= q)//r 对 q 取模
return fpow(U, r / q) * slv(p, q, r % q, n, U, R);
if (n == 0)
return R;
if (p >= q)//p 对 q 取模
return R * slv(p % q, q, r + p % q, n - 1, U, fpow(U, p / q) * R);
if (p == 0)//终止条件
return fpow(R, n + 1);
ll m = (p * n + r) / q;
if (m == 0)
return fpow(R, n + 1);
return slv(q, p, p + q - r - 1, m - 1, R, U) * fpow(R, n - (m * q - r - 1) / p);//交换 p, q
}
int main() {
int T;
cin >> T;
while (T--) {
ll n, p, q, r;
cin >> n >> p >> r >> q;
Node U = Node(0, 1, 0);
Node R = Node(1, 0, 0);
Node ans = slv(p, q, r, n, U, R);
cout << ans.sumy << " " << ans.sqry << " " << ans.prod << endl;
}
return 0;
}
LOJ138. 类欧几里得算法
求 \(\sum x^ay^b\)。
我们考虑 \((x + \Delta x)^a(y + \Delta y)^b\) 分解之后的所有项,我们需要维护所有的 \(x^ny^m\) 即可。
P5171 Earthquake
求 \(ax + by \le c\) 非负整数解个数。
进行一些变化得到:
万欧求解即可。



