图论小记

三元环计数

无向图三元环计数指在 \(G=(V,E)\) 中有多少个无序点对 \((x,y,z)\) 满足 \((x,y),(y,z),(x,z) \in E\).

首先，我们将无向图转化成有向图，设 \(d_i\) 表示 \(i\) 的度数，我们按照 \(d_i\) 从小到大排序（相同则按编号从小到大），然后每条边由排在前的指向排在后的。

不难发现，原图中的三元环在新图中必然是 \(x\) 指向 \(y\) 和 \(z\)，\(y\) 指向 \(z\) 的形式。

所以我们枚举 \((x, y)\) 这条边，然后枚举所有 \(y\) 的出边指向节点 \(z\)，判断 \(z\) 是不是 \(x\) 指向的节点。具体实现可以向将所有 \(x\) 指向节点打标记，这样方便判断。

这个做法看似暴力，但是其时间复杂度是 \(O(m\sqrt{m})\) 的，因为我们可以证明新图中每个点的出度不超过 \(2\sqrt{m}\)。

证明不难，反证法，如果 \(d_x > 2\sqrt{m}\)，则所有 \((x,y)\) 的 \(y\) 也会 \(d_y > d_x > 2\sqrt{m}\)，这样总边数就超过了 \(m\)，于是证出这个结论。

这其实也间接证明了三元环的个数不超过 \(m\sqrt{m}\)，所以我们实际可以找出所有的三元环。这在解决一些问题时很有帮助。

• P1989 无向图三元环计数

模板题。

点击查看代码

#include <iostream>
#include <cstdio>
#include <vector>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1e5 + 5;
const int M = 2e5 + 5;

int n, m;
vector<int> e[N];
int d[N] = {0};

typedef pair<int, int> pii;
pii ed[M];

bool cmp(int x, int y) {//x是否在 y 前面 
	if (d[x] != d[y])
		return d[x] < d[y];
	return x < y;	
}

bool f[N] = {false};

int main() {
	cin >> n >> m;
	for (int i = 1, u, v; i <= m; i++) {
		cin >> u >> v;
		d[u]++, d[v]++;
		ed[i] = make_pair(u, v);
	}
	for (int i = 1; i <= m; i++) 
		if (cmp(ed[i].first, ed[i].second))
			e[ed[i].first].push_back(ed[i].second);
		else
			e[ed[i].second].push_back(ed[i].first);
	int ans = 0;
	for (int x = 1; x <= n; x++) {
		for (auto y: e[x])
			f[y] = true;
		for (auto y: e[x])
			for (auto z: e[y])
				if (f[z])
					ans++;
		for (auto y: e[x])
			f[y] = false;	
	}
	cout << ans << endl;
	return 0;
} 

• CF985G Team Players

不错的计数题。

显然原图的补图边数很多，肯定不能真的建出来找三元环。

考虑先算出所有点对的贡献，再减去不符合要求的点对的贡献。

按照三元环处理套路，还是建出新图，则不符合要求的有三种情况：三元环，一条链，一条边加上一个点。

分别去计数这几类的数量即可，注意一条链在计算时会将三元环算三次，二一条边加一个点会将一条链算两次，三元环算三次，最后要减去这些。

很多细节，代码有点长，不太好写。

• 有向图三元环计数问题

其实很简单，转化成无向图，显然所有有向图的三元环在无向图中还是三元环，找出无向图的三元环再判断即可。

• HDU6184 Counting Stars

不难。求出所有三元环，设 \(c_i\) 表示第 \(i\) 条边被几个三元环包含，答案就是 \(\sum_i \binom{c_i}{2}\)。

• #6076. 「2017 山东一轮集训 Day6」三元组

前置知识：莫比乌斯反演。

看到这种 \(\gcd(i,j)=1\) 的形式就要想到莫反， 我们要计算的就是：

\[\sum_{i=1}^a\sum_{j=1}^b\sum_{k=1}^c[\gcd(i,j)=1][\gcd(i,k)=1][\gcd(j,k)=1] \]

运用莫比乌斯函数和莫反套路，我们可以转化成：

\[\sum_{i=1}^a\sum_{j=1}^b\sum_{k=1}^c\mu(i)\mu(j)\mu(k)\lfloor\frac{a}{\operatorname{lcm}(i,j)}\rfloor\lfloor\frac{b}{\operatorname{lcm}(i,k)}\rfloor\lfloor\frac{c}{\operatorname{lcm}(j,k)}\rfloor \]

观察这个式子，这题数据范围 \(a,b,c \le 50000\)。

首先，有很多 \(\mu\) 取值都是 \(0\)，我们可以去掉它们。

其次，我们发现只有 \(\operatorname{lcm}(i,j) \le 50000\) 时才有贡献，考虑到这是三个数的问题，我们不妨将所有 \(\operatorname{lcm}(i,j) \le 50000\) 的连一条 \((i,j)\)。

现在我们就是要找出所有的三元环，然后计算贡献即可。

实测最后建出来的边其实不多，大概是 \(3\times 10^5\)，瓶颈在于建图。

我们没必要枚举 \(i,j\)，反过来想，枚举 \(\operatorname{lcm}(i,j)\) 然后枚举其所有因子，再判断是否可行即可。

• 无向图四元环计数

我们采用三元环重新标号的技巧，一个四元环会有以下几个情况：

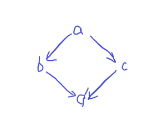
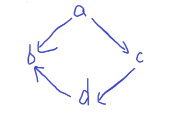
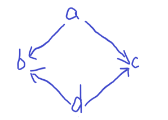
三元环经过标号后可以在 \(O(m\sqrt m)\) 的时间内枚举一条边加一个点的所有出度。

我们先考虑第一种，显然 a->b->d 和 a->c->d 是等价的，并且可以枚举得到，我们记 \(f_d\) 表示有多少条 a->?->d 的路径，则 \(\sum\binom{f_d}{2}\) 即是答案。

第三种和第一种类似，定义 \(g_d\) 表示有多少个 c<-?->d 我们可以用一样的技巧处理，但是第三种总个数需要除以二，因为会算两次。

再看第二种，不难发现其实就是第一种和第三种的混合版，\(\sum f_d g_d\) 就是答案。

点击查看代码

#include <iostream>
#include <cstdio>
#include <vector>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1e5 + 5;
const int M = 2e5 + 5;
typedef pair<int, int> pii;

int n, m;
vector<int> e[N], E[N];
pii ed[M];
int d[N] = {0};
bool cmp(int x, int y) {
    return d[x] == d[y] ? x < y : d[x] < d[y];
}

long long f[N] = {0}, g[N] = {0};
bool mrk[N] = {false};

int main() {
    cin >> n >> m;

    for (int i = 1, u, v; i <= m; i++) {
        cin >> u >> v;
        d[u]++, d[v]++;
        ed[i] = make_pair(u, v);
    }

    for (int i = 1; i <= m; i++)
        if (cmp(ed[i].first, ed[i].second))
            e[ed[i].first].push_back(ed[i].second);
        else
            e[ed[i].second].push_back(ed[i].first);

    for (int i = 1; i <= n; i++)
        for (auto j : e[i])
            E[j].push_back(i);

    long long ans = 0ll;

    //第一种
    for (int i = 1; i <= n; i++) {
        for (auto j : e[i])
            for (auto k : e[j])
                ans += f[k], f[k]++;

        for (auto j : e[i])
            for (auto k : e[j])
                f[k]--;
    }

    //第二种
    for (int i = 1; i <= n; i++) {
        for (auto j : e[i])
            for (auto k : e[j])
                f[k]++;

        for (auto j : E[i])
            for (auto k : e[j])
                if (k != i)
                    g[k]++;

        for (auto j : e[i])
            for (auto k : e[j])
                if (!mrk[k])
                    ans += 1ll * f[k] * g[k], mrk[k] = true;

        for (auto j : e[i])
            for (auto k : e[j])
                f[k]--, mrk[k] = false;

        for (auto j : E[i])
            for (auto k : e[j])
                if (k != i)
                    g[k]--;
    }

    //第三种
    long long res = 0ll;

    for (int i = 1; i <= n; i++) {
        for (auto j : E[i])
            for (auto k : e[j])
                if (k != i)
                    res += g[k], g[k]++;

        for (auto j : E[i])
            for (auto k : e[j])
                if (k != i)
                    g[k]--;
    }

    cout << ans + res / 2 << endl;
    return 0;
}

图论计数相关

记录一些有趣的计数题。

• [ABC262E] Red and Blue Graph

题意： 给一张无向图黑白染色，要求黑点恰好 \(k\) 个且所有两个端点不同色的边的个数为奇数，求方案数。\(n,m \le 10^5\)。

转化贡献，我们不妨设 \(i\) 颜色为 \(A_i\)，是一个 \(01\) 值。每条边的边权的贡献就是 \(A_i \oplus A_j\)，相同为 0，不相同为 1。

要求 \(\sum{A_u \oplus A_v} \% 2 = 0\)，不难发现，\((A_u \oplus A_v) \%2 = (A_u + A_v) \% 2\)。

所以我们要求 \(\sum{A_u + A_v} \% 2 = 0\)，这是个经典变化，可以变成 \(\sum{A_u \times d_u}\)，\(d_u\) 是度数。

所以我们只用关心度数即可，枚举奇数度数的点选了多少个，组合数计算即可。

点击查看代码

#include <iostream> 
#include <cstdio>
#include <vector>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 2e5 + 5;
const int mod = 998244353;

int fpow(int a, int b, int p) {
	if (b == 0)
		return 1;
	int ans = fpow(a, b / 2, p);
	ans = (1ll * ans * ans) % p;
	if (b % 2 == 1)
		ans = (1ll * a * ans) % p;
	return ans;
}

int fac[N] = {0}, inv[N] = {0};
void init(int n) {
	fac[0] = 1;
	for (int i = 1; i <= n; i++)
		fac[i] = (1ll * fac[i - 1] * i) % mod;
	inv[n] = fpow(fac[n], mod - 2, mod);
	for (int i = n - 1; i >= 0; i--)
		inv[i] = (1ll * inv[i + 1] * (i + 1)) % mod;
}
int cmb(int n, int m) {
	if (n < m)
		return 0;
	return 1ll * fac[n] * inv[m] % mod * inv[n - m] % mod;
}

int n, m, k, d[N] = {0};


int main() {
	cin >> n >> m >> k;
	init(n);
	for (int i = 1, u, v; i <= m; i++) {
		cin >> u >> v;
		d[u]++, d[v]++;
	}
	int odd = 0, even = 0;
	for (int i = 1; i <= n; i++)
		if (d[i] % 2 == 1)
			odd++;
		else
			even++;
	int ans = 0;
	for (int i = 0; i <= odd && i <= k; i += 2) 
		ans = (ans + 1ll * cmb(even, k - i) * cmb(odd, i) % mod) % mod;
	cout << ans << endl;
	return 0;
} 

深搜树

深搜树是点双，边双等算法的基础，这里记录一些深搜树相关的好题。

• CF405E Graph Cutting

题意： \(n\) 个点 \(m\) 条边无向图，构造一个边的完全匹配，两条边能够匹配当且仅当有公共点。\(n,m \le 10^5\)

我们考虑如果是一棵树，我们可以从下往上，假设到了 \(x\)，\(x\) 子树除了与儿子的边都匹配了。如果剩下偶数条，刚好匹配玩，否则就和到 \(x\) 父亲匹配。显然只要 \(m % 2 = 0\) 就有解。

考虑深搜树，将回边挂在祖先那里，然后就类似树的构造即可。

• CF1364D Ehab's Last Corollary

题意： 一张无向图和一个数 \(k\)，要么找出一个大小不超过 \(k\) 的环，要么找出一个大小恰好为 \(\lceil\frac{k}{2}\rceil\) 的独立集。

我们考虑深搜树搜索得到的前 \(k\) 个点，如果有回边，构成的环大小不超过 \(k\)；否则搜到的是一棵树，最大的独立集大小大于等于 \(\lceil\frac{k}{2}\rceil\)，于是可以得到恰好的独立集。

• CF1391E Pairs of Pairs

题意： 一张无向图，要么找出长度至少为 \(\lceil \frac{n}{2} \rceil\) 的简单路径，要么选出至少 \(\lceil \frac{n}{2} \rceil\) 个点两两匹配，使得任意两个匹配的四个点的导出子图至多 \(2\) 条边。

还是深搜树，如果存在深度大于等于 \(\lceil \frac{n}{2} \rceil\) 的点，输出到根的路径即可。

否则把深度相同的点两两匹配，至少匹配了 \(n - \lceil \frac{n}{2} \rceil + 1 \ge \lceil \frac{n}{2} \rceil\) 个点，满足条件。