转载:【AI系统】算子融合
近年来,人们对优化神经网络模型的执行一直非常重视。算子融合是一种常见的提高神经网络模型执行效率的方法。这种融合的基本思想与优化编译器所做的传统循环融合相同,它们会带来:1)消除不必要的中间结果实例化,2)减少不必要的输入扫描;3)实现其他优化机会。下面让我们正式走进算子融合。
算子融合方式
在讨论算子融合之前,我们首先要知道什么是计算图,计算图是对算子执行过程形象的表示,假设 $C = { N, E, I, O}$ 为一个计算的计算表达,那么可以有:
- 计算图表示为由一个节点 N(Node),边集(Edge),输入边(Input),输出边(Output)组成的四元组
- 计算图是一个有向联通无环图,其中的节点也被称为算子(Operator)
- 算子必定有边相连,输入边,输出边不为空
- 计算图中可以有重边(两个算子之间可以由两条边相连)
于是当我们遇到一个具体的算子实例时,我们可以在其对应的计算图上做等价的融合优化操作,这样的抽象使我们能够更加专心于逻辑上的处理而不用在意具体的细节。
为什么要算子融合呢?这样有什么好处呢? 融合算子出现主要解决模型训练过程中的读入数据量,同时,减少中间结果的写回操作,降低访存操作。它主要想解决我们遇到的内存墙和并行强墙问题:
- 内存墙:主要是访存瓶颈引起。算子融合主要通过对计算图上存在数据依赖的“生产者-消费者”算子进行融合,从而提升中间 Tensor 数据的访存局部性,以此来解决内存墙问题。这种融合技术也统称为“Buffer 融合”。在很长一段时间,Buffer 融合一直是算子融合的主流技术。早期的 AI 框架,主要通过手工方式实现固定 Pattern 的 Buffer 融合。
- 并行墙:主要是由于芯片多核增加与单算子多核并行度不匹配引起。可以将计算图中的算子节点进行并行编排,从而提升整体计算并行度。特别是对于网络中存在可并行的分支节点,这种方式可以获得较好的并行加速效果。
算子的融合方式非常多,我们首先可以观察几个简单的例子,不同的算子融合有着不同的算子开销,也有着不同的内存访问效率提升。
- 假设我们有如图所示左侧的计算图,他有 4 个算子 $A,B,C,D$,此时若我们将 $C,D$ 做(可行的话)融合,此时可以减少一次的 Kernel 开销,也减少了一次的中间数据缓存。
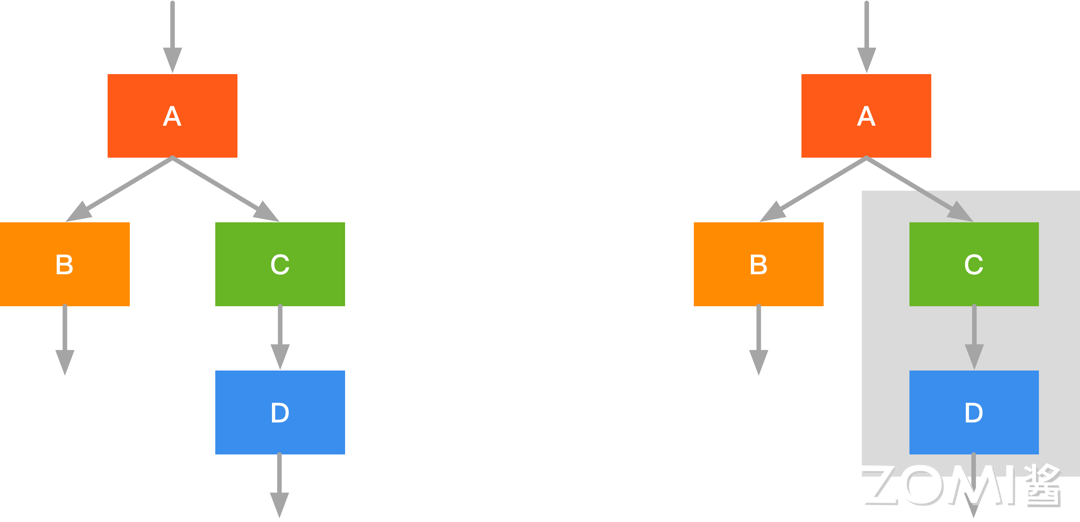
- 如图左侧部分的计算图,$B,C$ 算子是并行执行,但此时有两次访存,我们可以将 $A$“复制”一份分别与 $B,C$ 做融合,如图右侧所示,此时我们 $A,B$ 与 $A,C$ 可以并发执行且只需要一次的访存。
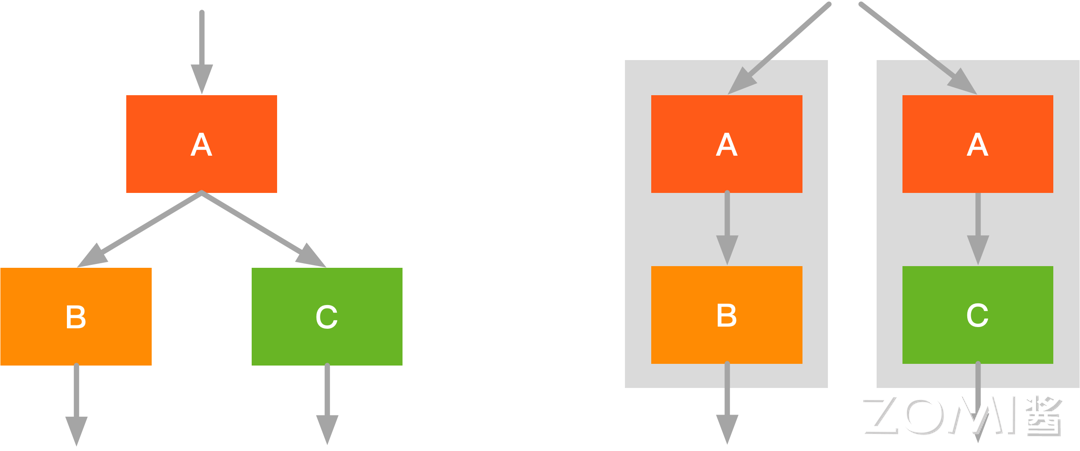
- 如图左侧部分的计算图(和 2 一致),此时我们可以变换以下融合的方向,即横向融合,将 $B,C$ 融合后减少了一次 Kernel 调度,同时结果放在内存中,缓存效率更高。
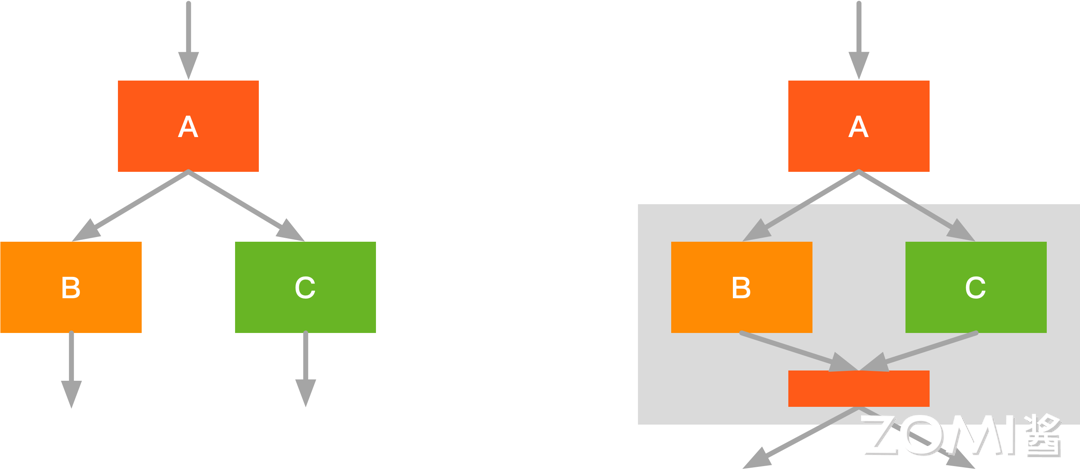
- 如图左侧部分的计算图所示,我们也可以将 $A,B$ 融合,此时运算结果放在内存中,再给 C 进行运算,此时可以提高内存运算效率。
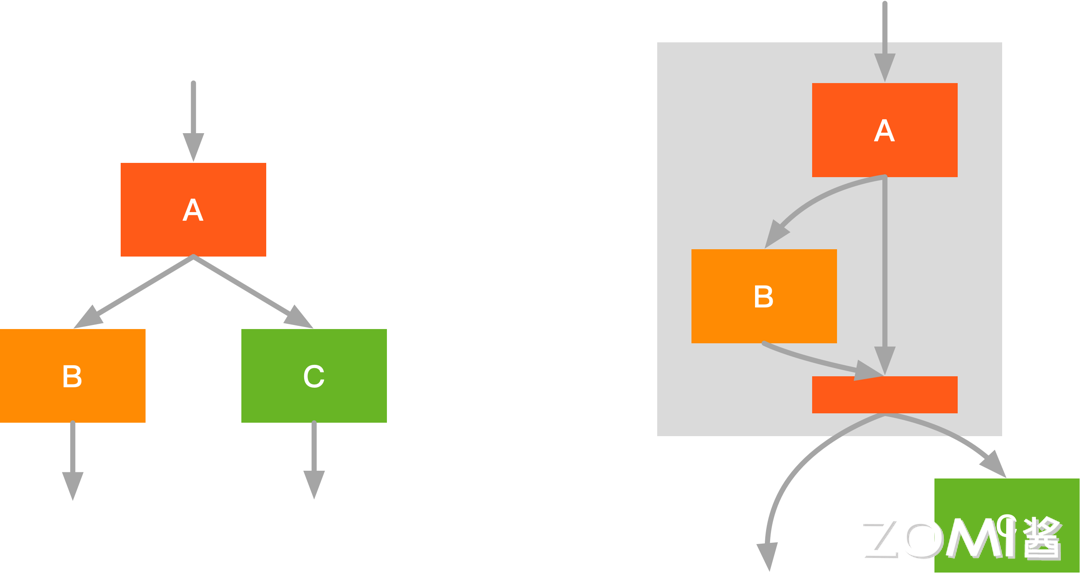
- 同样的,我们还可以将多个卷积核融合成一个卷积核,可以显著减少内存占用和访存的开销,从而提高卷积操作的速度。在执行如下图的卷积操作时,可以将两个卷积算子融合为一个算子,以增加计算复杂度为代价,降低访存次数与内存占用。
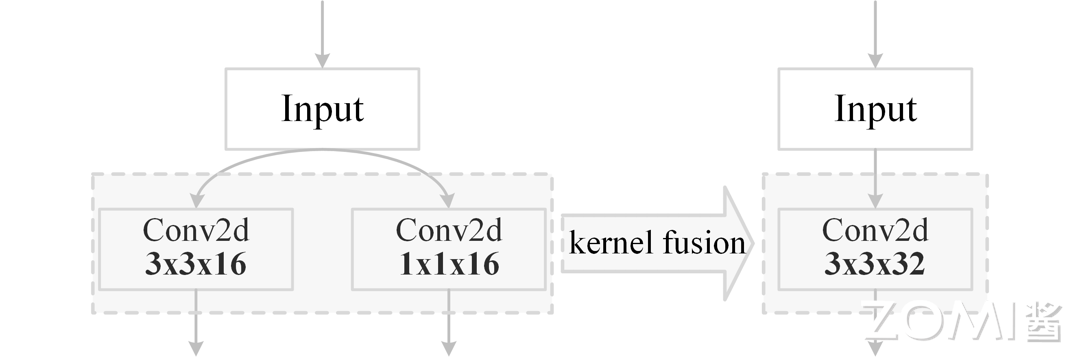
通过示例代码模拟卷积核扩张与融合过程,将两个卷积算子融合成一个更大的卷积算子,具体如下所示:
import torch
import torch.nn.functional as F
# kernel fusion 示例
if __name__ == "__main__":
torch.manual_seed(0)
# 生成输入
input = torch.randn(1, 3, 32, 32)
# 生成 conv1 的权重和偏,out_channels=16, in_channels=3, kernel_height=3, kernel_width=3
conv1_weight = torch.randn(16, 3, 3, 3)
conv1_bias = torch.randn(16)
conv1_output = F.conv2d(input, conv1_weight, bias=conv1_bias, stride=1, padding=1)
print('conv1_output: ', conv1_output)
# 生成 conv2 的权重和偏置,out_channels=16, in_channels=3, kernel_height=1, kernel_width=1
conv2_weight = torch.randn(16, 3, 1, 1)
conv2_bias = torch.randn(16)
conv2_output = F.conv2d(input, conv2_weight, bias=conv2_bias, stride=1, padding=0)
print('conv2_output: ', conv2_output)
# kernel fusion
# 将 conv2 的卷积核权重由(1, 1)扩展到(3, 3)
weight_expanded = torch.zeros(16, 3, 3, 3)
weight_expanded[:, :, 1, 1] = conv2_weight[:, :, 0, 0]
# conv1 卷积核与 conv2 卷积核融合
weight_fusion = torch.concatenate([conv1_weight, weight_expanded], dim=0)
# conv1 偏置与 conv2 偏置融合
bias_fusion = torch.concatenate([conv1_bias, conv2_bias], dim=0)
# 1 次融合后的权重与偏置卷积,替代 conv1 与 conv2 两次卷积
kernel_fusion_output = F.conv2d(input, weight_fusion, bias=bias_fusion, stride=1, padding=1)
print(kernel_fusion_output)
最后我们给一个更具体的算子融合,读者可自行验证。
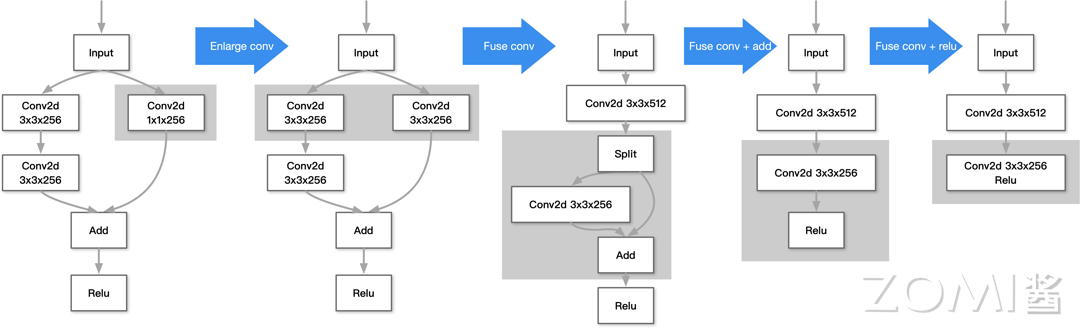
如图所示,首先我们可以利用横向融合的思想,将一个 3×3×256 的卷积算子和一个 1×1×256 的卷积算子通过 Enlarge 方法将后者扩成 3×3×256 的卷积算子,然后融合成一个 3×3×512 的卷积算子;接着我们可以利用纵向融合的思想,将 Split,卷积,Add 融合成一个卷积算子,减少 Kernel 调度;最后,一般激活 ReLU 都可以和前一个计算步骤融合,于是最后融合得到一个 Cov2d_ReLU 算子。于是我们从一个比较复杂的计算图,最终得到了一个比较简洁的计算图,减少了 Kernel 调度,实现了“少就是多”。
总而言之,为了提高效率,我们可以通过消除不必要的中间结果实例化、 减少不必要的输入扫描、 发现其他优化机会等方法来指导我们实现算子融合。
算子融合案例
Batch-Normalization (BN)是一种让神经网络训练更快、更稳定的方法(faster and more stable)。它计算每个 mini-batch 的均值和方差,并将其拉回到均值为 0 方差为 1 的标准正态分布。BN 层通常在 nonlinear function 的前面/后面使用。
下面我们以 Conv-BN-ReLU 的算子融合作为例子。
BN 计算流程
BN 的计算公式
计算均值:
$$
\mu_B = \frac{1}{m} \sum_{i=1}^{m} x_i
$$
计算方差:
$$
\sigma_B^2 = \frac{1}{m} \sum_{i=1}^{m} (x_i - \mu_B)^2
$$
归一化:
$$
\hat{x}_i = \frac{x_i - \mu_B}{\sqrt{\sigma_B^2 + \epsilon}}
$$
其中,$\epsilon$ 是一个很小的正数,用于避免除以零。
线性变换:
$$
y_i = \gamma \hat{x}_i + \beta
$$
其中,$\gamma$ 和 $\beta$ 是可学习的缩放参数和偏移参数。
在 BN 前向计算过程中,首先求输入数据的均值 $\mu$ 与方差 $\sigma^{2}$,然后使用 $\mu$、$\sigma^{2}$ 对每个输入数据进行归一化及缩放操作。其中,$\mu$、$\sigma^{2}$ 依赖于输入数据;归一化及缩放计算的输入则依赖于输入数据、均值、方差以及两个超参数。下图为前向计算过程中 BN 的数据依赖关系:

其中,$\gamma$ 和 $\beta$ 是一个可学习的参数,在训练过程中,和其他层的权重参数一样,通过梯度下降进行学习。在训练过程中,为保持稳定,一般使用滑动平均法更新 $\mu$ 与 $\sigma^{2}$,滑动平均就是在更新当前值时,保留一定比例上一时刻的值,以均值 $\mu$ 为例,根据比例 $\theta$(如,$\theta=0.99$)保存之前的均值,当前只更新 $1-\theta$ 倍的本 Batch 的均值,计算方法如下:
$$
\mu_{i}=\theta_{\mu_{i-1}}+(1-\theta)\mu_{i}
$$
BN 反向计算过程中,首先求参数误差;然后使用参数误差 $\Delta\gamma$、$\Delta\beta$ 计算输入误差 $\Delta X$ 。参数误差导数依赖于输出结果误差 $\Delta Y$ 以及输入 $X$;输入误差 $\Delta X$ 依赖于参数误差导数及输入 $X$、输出误差 $\Delta Y$。反向过程包括求参数误差以及输入误差两部分,BN 反向计算的关键访存特征是两次使用输入特征 $X$ 及输出误差$\Delta Y$,分别用于计算参数误差 $\Delta\gamma$、$\Delta\beta$ 及输入数据误差 $\Delta X$。
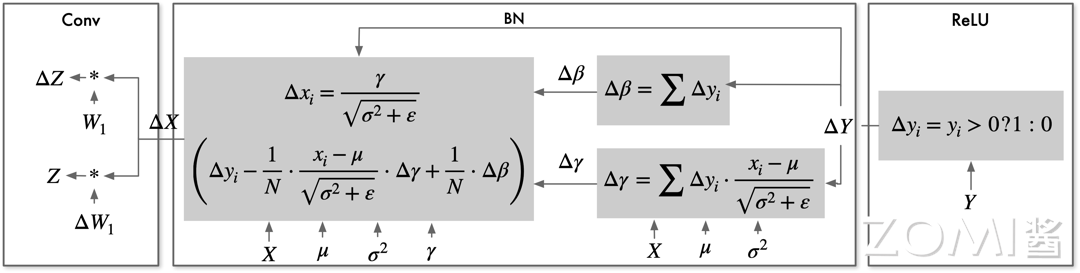
计算访存分析
网络模型训练时,需要保存每层前向计算时输出结果,用于反向计算过程参数误差、输入误差的计算。但是随着神经网络模型的加深,需要保存的中间参数逐渐增加,需要消耗较大的内存资源。由于加速器片上缓存容量十分有限,无法保存大量数据。因此需将中间结果及参数写出到加速器的主存中,并在反向计算时依次从主存读入使用。
前向计算过程中,每层的计算结果需写出主存,用于反向计算过程中计算输入误差;反向计算过程中,每层的结果误差也需写出到主存,原因是反向计算时 BN 层及卷积层都需要进行两次计算,分别求参数误差及输入数据误差,$X$、$\Delta Y$ 加载两次来计算参数误差 $\Delta\gamma$、$\Delta\beta$ 及输入误差 $\Delta X$ 。ReLU 输入 $Y$ 不需要保存,直接依据结果 $Z$ 即可计算出其输入数据误差。
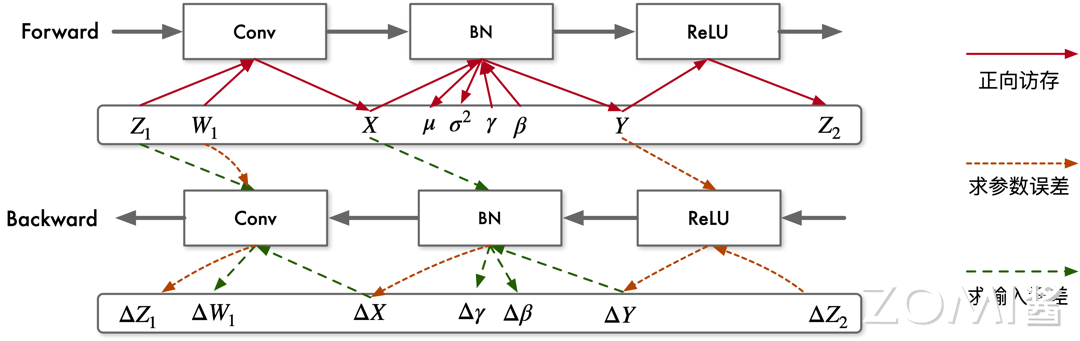
算子融合
前向过程中,BN 重构为两个子层:$BN_A$ 和 $BN_B$。
其中 $BN_A$ 计算均值与方差,$BN_B$ 完成归一化与缩放,分别融合于相邻卷积层及激活层。首先从主存读取输入 $X$、均值 $\mu$、方差 $\sigma^{2}$ 、参数 $\gamma$、$\beta$,计算 $BN_B$,完成归一化及缩放计算,将结果 Y 用于激活计算,输出 $Z$ 用于卷积计算,卷积结果 $X^{'}$ 写出到主存之前,计算 $BN_A$,即求均值 $\mu^{'}$ 与方差 $\sigma^{2}$。
最终完成“归一化缩放->激活层->卷积层->计算卷积结果均值与方差”结构模块的前向计算过程只需要读取一次,并写回卷积计算结果 $X^{'}$ 及相关参数。
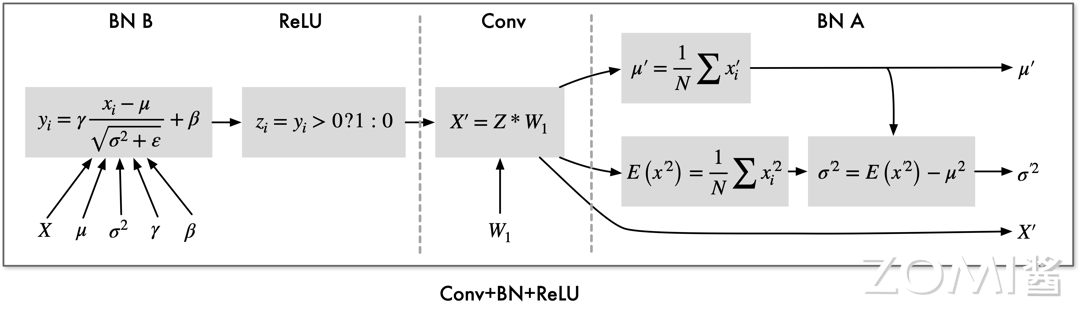
具体融合计算过程如下所示:
- 卷积计算:
$$
{z} = {w} * {x} + {b}
$$
- BN 计算:
$$
y = \gamma\frac{{\left( {z - mean} \right)}}{{\sqrt {\operatorname{var} } }} + \beta
$$
-
ReLU 计算:
$$
y=max(0,y)
$$ -
融合卷积、BN 与 ReLU 的运算:
将卷积计算公式带入到 BN 计算公式中,可得到下式:
$$
y = \gamma\frac{{\left( {(w*x+b) - mean} \right)}}{{\sqrt {\operatorname{var} } }} + \beta
$$展开后可得到:
$$
y =\gamma\frac{w}{{\sqrt {\operatorname{var}}}}*x+\gamma\frac{{\left( {b - mean} \right)}}{{\sqrt {\operatorname{var} } }} + \beta
$$也即将卷积与 BN 融合后的新权重 $w'$ 与 $b'$,可表示为如下所示:
$$
w' = \gamma\frac{w}{{\sqrt {\operatorname{var} } }}\
b' = \gamma\frac{{\left( {b - mean} \right)}}{{\sqrt {\operatorname{var} } }} + \beta$$
最后,将卷积、BN 与 ReLU 融合,可得到如下表达式:
$$
y=max(0,w'*x+b')
$$
TVM 融合规则与算法
TVM是一个端到端的机器学习编译框架,它的目标是优化机器学习模型让其高效运行在不同的硬件平台上。它前端支持 TensorFlow、Pytorch、MXNet、ONNX 等几乎所有的主流框架。它支持多种后端(CUDA、ROCm、Vulkan、Metal、OpenCL、LLVM、C、WASM)及不同的设备平台(GPU、CPU、FPGA 及各种自定义 NPU)。
TVM 主要用于推理场景。在架构上,主要包括 Relay 和 TIR 两层。其通过 Relay 导入推理模型,随后进行融合优化,最后通过 TIR 生成融合算子。TVM 整体的算子融合策略是基于支配树来实现的,下面将介绍支配树等相关概念。
TVM 支配树
支配树与支配点:
- 支配树:各个点的支配点构成的树
- 支配点:所有能够到达当前节点的路径的公共祖先点( Least Common Ancestors,LCA)
具体而言,对于一张有向图(可以有环)我们规定一个起点 $r$,从 $r$ 点到图上另一个点 $w$ 可能存在很多条路径(下面将 $r$ 到 $w$ 简写为 $r→w$)。如果对于 $r→w$ 的任意一条路径中都存在一个点 $p$,那么我们称点 $p$ 为 $w$ 的支配点(也可以称作是 $r→w$ 的必经点),注意 $r$ 点不讨论支配点。
下面用 $idom[u]$ 表示离点 $u$ 最近的支配点。对于原图上除 $r$ 外每一个点 $u$,从 $idom[u]$ 向 $u$ 建一条边,最后我们可以得到一个以 $r$ 为根的树。这个树我们就叫它"支配树"。
如下图所示,到达 Node8 的路径有 Node3->4->7->8,Node3->5->7->8,Node3->6->7->8,因此 Node4,Node5,Node6,Node7 为 Node8 的支配点。
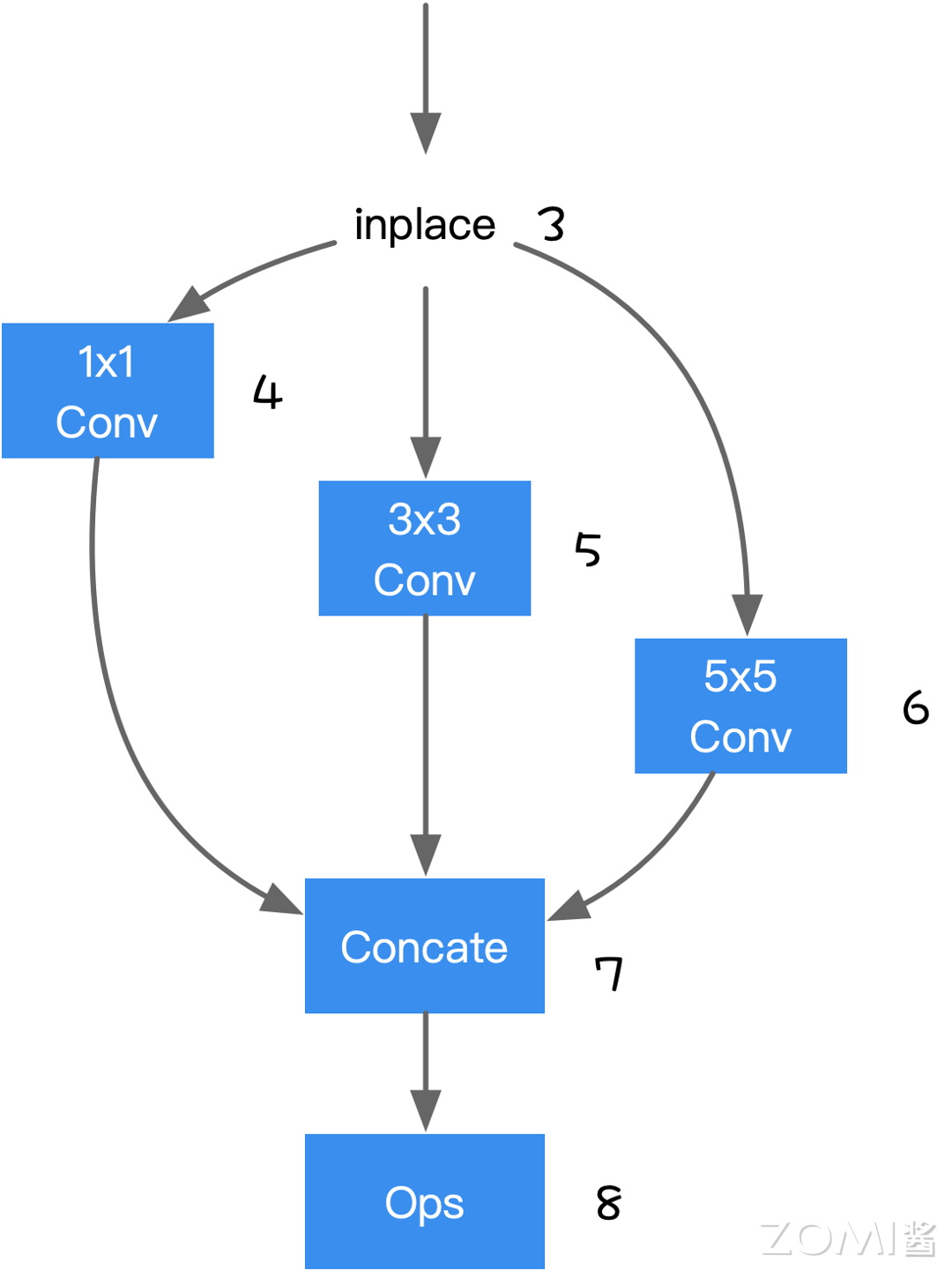
TVM 的算子融合策略就是检查每个 Node 到其支配点的 Node 是否符合融合条件,如果符合就对其进行融合。如上图,检查 Node4->Node7->Node8 是否能融合,若可以融合,则用新的算子替代原来路径上的算子。因此支配树作用如下:
- 检查每个 Node 到其支配点的 Node 是否符合融合条件
- 融合的基本规则是融合掉的 Node 节点不会对剩下的节点产生影响
支配树生成方式:
- 根据 DAG 进行深度优先遍历,生成 DFS 树;注意,生成的 DFS 树是倒序的,也即最后一个节点为 0,然后依次递增
- 根据 DFS 树及对应的边生成 DOM 树
- 使用 Group 来描述多个 Node 是否能被融合;如果一个算子不能和任何其他算子融合,那么这个 group 就只有一个独立的算子;如果几个算子能够融合,则能融合的算子就构成了一个 group
TVM 算子融合流程
TVM 算子融合流程如下:
- 通过 AST 转换为 Relay IR,遍历 Relay IR
- 建立 DAG 用于后支配树分析
- 应用算子融合算法,遍历每个 Node 到它的支配点的所有路径是否符合融合规则,完成融合后,遍历节点创新的 DAG 图
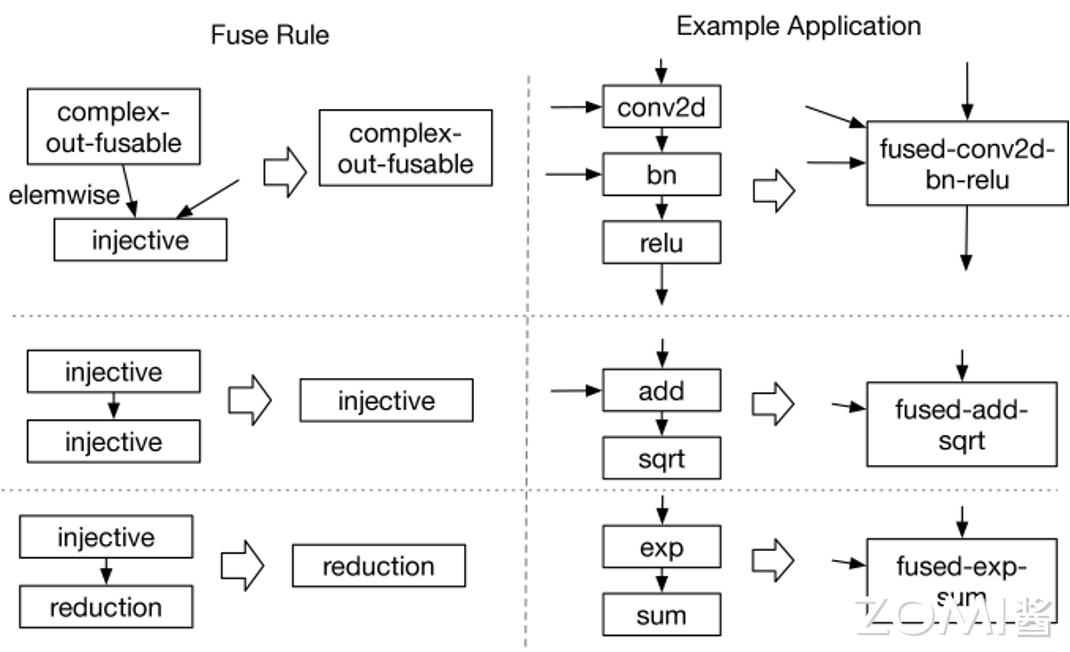
TVM 提供了 4 种融合规则,具体如下:
- injective(one-to-one map):映射函数,比如加法,点乘等。
- reduction:约简,如 sum/max/min,输入到输出具有降维性质,如 sum/max/min。
- complex-out-fusable(can fuse element-wise map to output):计算复杂类型的融合,如 conv2d。
- opaque(cannot be fused):无法被融合的算子,如 sort。
如果您想了解更多AI知识,与AI专业人士交流,请立即访问昇腾社区官方网站https://www.hiascend.com/或者深入研读《AI系统:原理与架构》一书,这里汇聚了海量的AI学习资源和实践课程,为您的AI技术成长提供强劲动力。不仅如此,您还有机会投身于全国昇腾AI创新大赛和昇腾AI开发者创享日等盛事,发现AI世界的无限奥秘~
转载自:| https://www.cnblogs.com/ZOMI/articles/18558994 | header |
| ---------------------------------------------- | ------ |
| | |



