数据挖掘——特征工程
特征工程(Feature Engineering)
特征工程其本质上是一项工程活动,它的目的是最大限度地从原始数据中提取特征以供算法和模型使用。
特征工程的重要性:
- 特征越好,灵活性越强
- 特征越好,模型越简单
- 特征越好,性能越出色
数据和特征决定了机器学习的上限,而模型和算法只是逼近这个上限。特征工程的最终目的就是提升模型的性能。
特征工程包括:数据处理、特征选择、维度压缩三大方面的内容。
1、数据处理:量纲不一、虚拟变量、缺失值填充
1.1、量纲不一
量纲就是单位,特征的单位不一致就不能放在一起比较,可以使用数据标准化的方法来达到量纲一致的要求。
常用的数据标准化方法:0-1标准化、Z标准化、归一化
1.1.1 0-1标准化
0-1标准化是对原始数据进行线性变化,将特征值映射成区间为[0,1]的标准值中。
标准化值 = 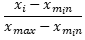
导入一份含电影票房和豆瓣评分的数据如下
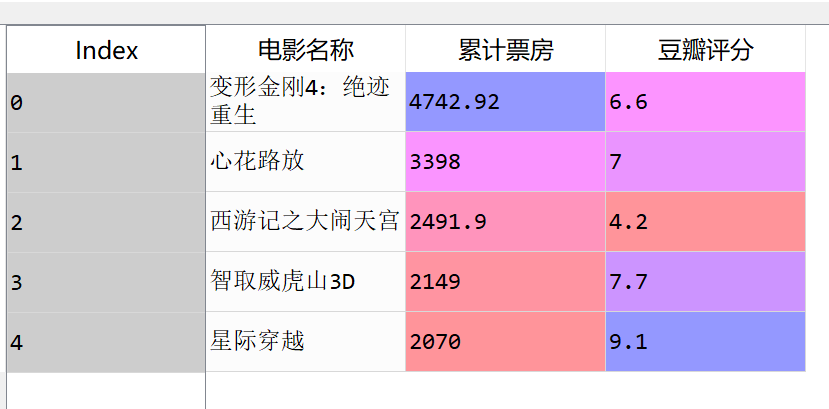
基于sklearn包的0-1标准化:
scaler = MinMaxScaler() data['票房0-1标准化'] = scaler.fit_transform(np.array(data['累计票房']).reshape(5, -5)) data['评分0-1标准化'] = scaler.fit_transform(np.array(data['豆瓣评分']).reshape(5, -5))
1.1.2 Z标准化
Z标准化是基于特征值的均值和标准差进行数据的标准化,标准化后的变量围绕0上下波动,大于0说明高于平均水平,小于0说明低于平均水平。
标准化值 = 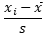
基于sklearn包的Z标准化:
from sklearn.preprocessing import scale data['票房z标准化'] = scale(data['累计票房']) data['评分z标准化'] = scale(data['豆瓣评分'])
1.2、 虚拟变量
虚拟变量也叫哑变量或离散特征编码,可用来表示分类变量、非数量因素可能产生的影响。
python中主要通过pandas包中的get_dummies方法进行特征变量的虚拟化。
1.3、缺失值
缺失值产生的原因:有些信息暂时无法获取(单身人士的配偶、未成年人的收入等);有些信息被遗漏或错误的处理了
缺失值处理方法:数据补齐;删除缺失值;不处理
from sklearn.preprocessing import Imputer # mean, median, most_frequent 三种处理参数 imputer = Imputer(strategy='mean') imputer.fit_transform(data2[['累计票房']])
2、 特征选择:
如何选择特征:考虑特征是否发散;考虑特征与目标相关性
以以下格式的数据为例,用不同方法得到特征
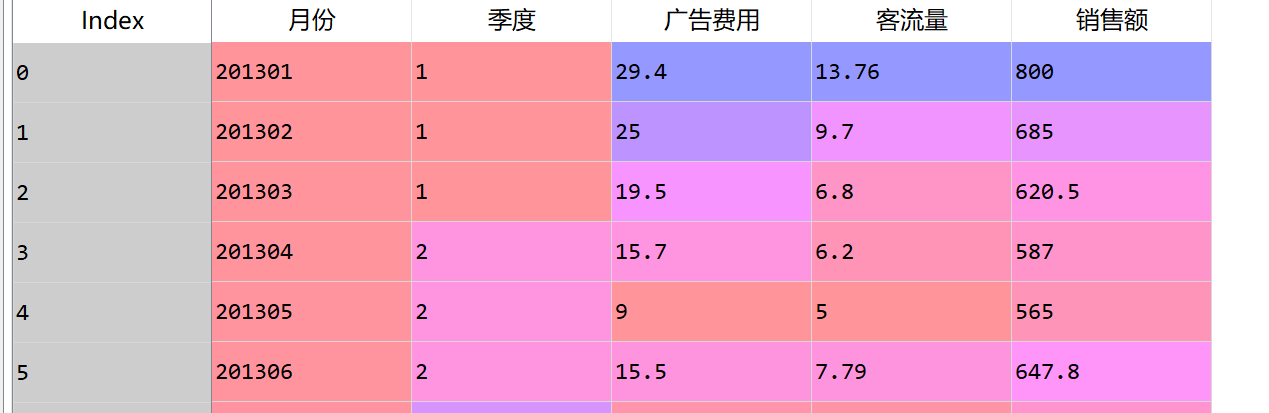
2.1 、方差选择法
先计算各个特征的方差,根据阈值,选择方差大于阈值的特征
基于sklearn包的方差选择获取特征的方法
from sklearn.feature_selection import VarianceThreshold varianceThreshold = VarianceThreshold(threshold=10) #设置方差阈值,只选择方差大于10的特征 varianceThreshold.fit_transform(data[['累计票房', '豆瓣评分']]) data[['累计票房', '豆瓣评分']].std() #计算两列各自的方差,其中豆瓣评分方差为1.79,低于10 varianceThreshold.get_support() #得到选择特征的列的序号
2.2、 相关系数法
先计算各个特征对目标值的相关系数,选择更加相关的特征
from sklearn.feature_selection import SelectKBest from sklearn.feature_selection import f_regression selectbest =SelectKBest(f_regression, k=2) #设置通过回归的方法, 选择数量为2个的特征 feature = data1[['月份','季度','广告费用','客流量']] #变量矩阵 bestfeature = selectbest.fit_transform(feature,data1['销售额']) #得到与销售额相关度最高的2个变量 feature.columns[selectbest.get_support()] #获得特征列的名称
2.3、 递归特征消除法
使用一个基模型来进行多轮训练,经过多轮训练后,保留指定的特征数
from sklearn.feature_selection import RFE from sklearn.linear_model import LinearRegression #选择线性回归模型, 保留2 个特征 rfe = RFE(estimator= LinearRegression(), n_features_to_select=2) sFesture = rfe.fit_transform(feature, data1['销售额']) rfe.get_support()
2.4、 模型选择法
将建好的模型对象传入选择器,然后它会根据这个建好的模型,自动选择最好的特征值
from sklearn.feature_selection import SelectFromModel lrmodel = LinearRegression() #先创建一个线性回归对象 selectmodel = SelectFromModel(lrmodel) selectmodel.fit_transform(feature,data1['销售额']) feature.columns[selectmodel.get_support()]
3、 维度压缩
特征选择完成后,可以直接训练模型,但可能由于特征矩阵过大,导致计算量和计算时间大,因此需要降低矩阵维度。
主成分分析(PCA)就是最常用的数据降维方法:在减少数据维度的同时,保持对方差贡献最大的特征。
以iris数据集为例,将四维数据转化成三维、二维数据
from sklearn import datasets iris = datasets.load_iris() data_iris = iris.data target = iris.target from sklearn.decomposition import PCA pca_3 = PCA(n_components=3) #创建一个维度为3维的PCA对象 data_pca_3 = pca_3.fit_transform(data_iris) #将iris数据集降至三维
将三维图形绘制出来
import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D colors = {0:'r', 1:'b', 2:'k'} markers = {0:'x', 1:'D', 2:'o'} fig = plt.figure(1, figsize=(8, 6)) ax = Axes3D(fig, elev=-150, azim=110) data_pca_gb = pd.DataFrame(data_pca_3).groupby(target) for g in data_pca_gb.groups: ax.scatter( data_pca_gb.get_group(g)[0], data_pca_gb.get_group(g)[1], data_pca_gb.get_group(g)[2], c=colors[g], marker=markers[g], cmap=plt.cm.Paired)
得到如下的三维图形
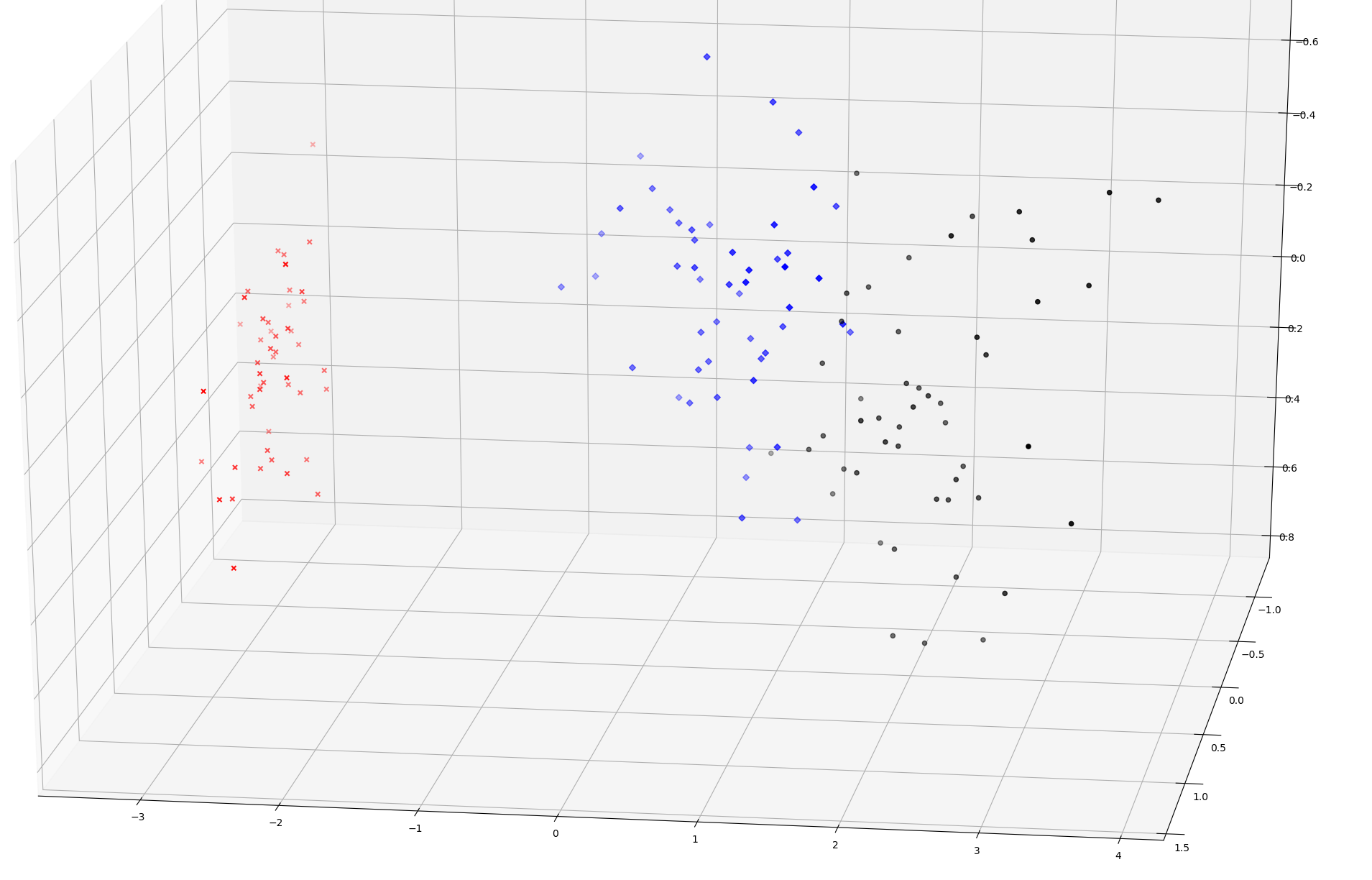
将数据降至二维同理
pca_2 = PCA(n_components=2) data_pca_2 = pca_2.fit_transform(data_iris) data_pca_gb = pd.DataFrame(data_pca_2).groupby(target)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号