数据挖掘——回归分析

回归分析（Regerssion Analysis）

——研究自变量与因变量之间关系形式的分析方法，它主要是通过建立因变量y 与影响他的自变量X_i之间的回归模型，来预测因变量y 的发展趋势。

一、回归分析的分类

线性回归分析

简单线性回归分析
多重线性回归分析

非线性回归分析

逻辑回归
神经网络

二、回归分析的步骤：

根据预测目标，确定自变量与因变量
绘制散点图，确定回归模型类型
估计模型参数，建立回归模型
对回归模型进行检验
利用回归模型进行预测

简单线性回归模型： y = a + bx + e （e为随机误差，∑e_i² 为残差，是判断模型拟合好坏的重要指标），使用最小二乘法获得模型参数

　　回归方程的精度就是用来表示实际观测点和回归方程的拟合程度的指标，使用判定系数来度量。

　　判定系数 = 相关系数R² = ESS/TSS = 1- (RSS/TSS) ，其中TSS 为总离差平方和，ESS 为回归平方和，RSS 为残差平方和

#绘制散点图和相关系数
plt.scatter(data.广告投入,data.销售额)
data.corr()

#估计模型参数，建立回归模型
lrmodel = LinearRegression()
x = data[['广告投入']]
y = data[['销售额']]

#训练模型
lrmodel.fit(x,y)

#对模型进行检验,得到模型评分
lrmodel.score(x,y)

#利用模型进行预测，自变量需要用数组进行传入
lrmodel.predict([[50]])

#查看参数
a = lrmodel.intercept_[0]
b = lrmodel.coef_[0][0]

多重线性回归模型（Multiple Linear Regression）： y = a + b₁x₁+ b₂x₂ + b₃x₃+ ……+ b_nx_n+ e （e为随机误差，∑e_i² 为残差，是判断模型拟合好坏的重要指标），使用最小二乘法获得模型参数

　　回归方程的精度就是用来表示实际观测点和回归方程的拟合程度的指标，使用判定系数来度量。

　　调整判定系数 = 相关系数R² = ESS/TSS = 1- [RSS/(n-k-1)] / [TSS/(n-1)] ，其中TSS 为总离差平方和，ESS 为回归平方和，RSS 为残差平方和，n为样本个数，k为变量个数

import matplotlib
from pandas.tools.plotting import scatter_matrix

#绘制两两之间的散点图并得到相关系数
font = {'family':'SimHei'}
matplotlib.rc('font',**font)
scatter_matrix(data_1[['店铺的面积','距离最近的车站','月营业额']],
               figsize=(10,10),diagonal='kde')
data_1[['店铺的面积','距离最近的车站','月营业额']].corr()
#估计模型参数，建立回归模型
lrmodel_1 = LinearRegression()
x1 = data_1[['店铺的面积','距离最近的车站']]
y1 = data_1[['月营业额']]

#训练模型
lrmodel_1.fit(x1,y1)

#对模型进行检验,得到模型评分
lrmodel_1.score(x1,y1)

#利用模型进行预测，自变量需要用数组进行传入
lrmodel_1.predict([[10,110]])
lrmodel_1.predict([[10,110],[20,120]])

#查看参数
a1 = lrmodel_1.intercept_[0]
b1 = lrmodel_1.coef_[0][0]
b2 = lrmodel_1.coef_[0][1]

一元非线性回归模型（Univariate Nonlinear Regression）：只包括一个自变量和一个因变量，且二者的关系可用一条曲线近似表示，则称为一元非线性回归（一元n次方程）

y = a₂x²+ a₁x¹ + a₀x⁰ （一元二次方程）

核心思想：用换元法将一元多次方程转化为多元一次方程

使用的关键类：from sklearn.preprocessing import PolynomialFeatures

例如：两个变量的散点图类似于一元二次方程的一部分，所以可以使用一元二次方程作为模型；

为了得到模型的结果，需要生成一个次方为2次的转换类对象：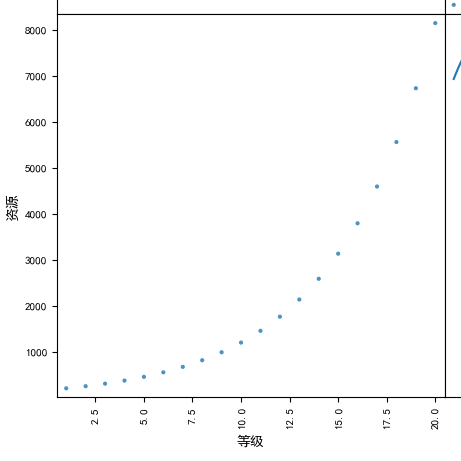

pf = PolynomialFeatures(degree=2) #degree为次数

x_2_fit = pf.fit_transform(x) #转换后的自变量，得到包含x及x²的数组

####核心思想：将一元n次方程，转换为多元线性方程
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
#生成一个次方为2次的转换类对象
x
pf = PolynomialFeatures(degree=2) 
x_2_fit = pf.fit_transform(x)

#模型测试及后续
lrmodel = LinearRegression()

lrmodel.fit(x_2_fit,y)
lrmodel.score(x_2_fit,y)

#训练后输入因变量时，同样需要将原始的因变量通过fit_transform方法进行转换，再得到预测结果
x_2_predict = pf.fit_transform([[21]])
x_2_predict = pf.fit_transform([[22],[23]])

lrmodel.predict(x_2_predict)

逻辑回归模型 (Logistic Regression)：针对因变量为分类变量而进行回归分析的一种统计方法，属于概率型非线性回归

优点：算法易于实现和部署，执行效率和准确度高

缺点：离散型的自变量数据需要通过生成虚拟变量的方式来使用

s型函数（Sigmoid Function） : 将连续数据变为（0，1）的范围，即归一化，将连续型数据变换为离散型数据的方法

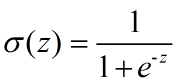
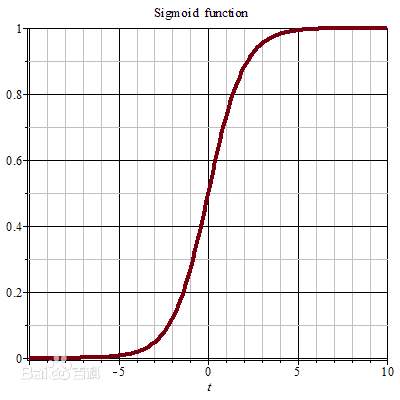
当z为0的时候，函数值为0.5；随着z的增大，函数值逼近于1；随着z的减小，函数值逼近于0.

所以，这个函数很适合做我们刚才提到的二分类的分类函数。假设输入数据的特征是(x0, x1, x2, ..., xn)，我们在每个特征上乘以一个回归系数 (w0, w1, w2, ... , wn)，然后累加得到sigmoid函数的输入z：

那么，输出就是一个在0~1之间的值，我们把输出大于0.5的数据分到1类，把输出小于0.5的数据分到0类。这就是Logistic回归的分类过程。

我们要做的，就是确定这个分类器中的最佳回归系数，即(w0, w1, w2, ... , wn)

使用python进行逻辑回归预测的步骤

1、读取训练集

2、对数据进行预处理，用虚拟变量来处理非数值变量

　　离散特征取值没有大小意义的处理函数 pd.get_dummies ,例如性别、结果为是/否的变量。也可以用来处理答案有多种，但没有次序区分的变量，即用几个变量作为一组（输入都是0/1）来表示某个分类变量，例如手机运营商的选择，可以由运营商1（是/否）、运营商2（是/否）、运营商3（是/否）……这样的一组变量来表示。

#选择部分非数值变量转化为虚拟变量
dummycolumns = ['Gender','Home Ownership','Internet Connection',
                'Marital Status','Movie Selector','Prerec Format',
                'TV Signal']
for column in dummycolumns:
    data1[column] = data1[column].astype('category')

dummyData = pd.get_dummies(data,columns=dummycolumns,
                           prefix=dummycolumns,
                           prefix_sep=' ',
                           drop_first=True)

　　离散特征之间有大小意义的处理函数 pd.series.map (dict) ,例如学历、看电影的频率等，需要先设置虚拟变量对应的值，以学历为例，需要按学历高低，赋予有序的值

#以学历为例，需要按学历高低，赋予有序的值
educationLevelDict = {
    'Post-Doc': 9,
    'Doctorate': 8,
    'Master\'s Degree': 7,
    'Bachelor\'s Degree': 6,
    'Associate\'s Degree': 5,
    'Some College': 4,
    'Trade School': 3,
    'High School': 2,
    'Grade School': 1}
#按学历构建虚拟变量后，作为新列加入到数据框中
dummyData['Education Level Map'] = dummyData['Education Level'].map(educationLevelDict)

3、根据虚拟化后的新的数据集构建模型，选择需要的变量

dummySelect=[ ……]
#设置输入项为刚才选取的变量
inputData = dummyData[dummySelect]
#设置输出项为 series1
outputData = dummyData[['series1']]

4、模型构建、训练、评分

from sklearn import linear_model
lrModel = linear_model.LogisticRegression()
lrModel.fit(inputData, outputData)
lrModel.score(inputData, outputData)

5、模型的使用

由于参数是以虚拟变量的形式进行输入的，所以对未知数据集需要进行同样的虚拟化操作，让后将变量作为参数进行传入，然后再得到预测结果

#对测试集进行同样的虚拟化操作

#输入测试集作为参数
inputNewData = dummyNewData[dummySelect]
#得到预测结果，以序列形式进行输出
lrModel.predict(inputNewData)

最终得到按序列形式输出的预测结果

posted @ 2018-10-04 19:38 没有神保佑的瓶子阅读(4385) 评论(0) 编辑收藏举报

没有神保佑的瓶子

数据挖掘——回归分析

公告