Boosting算法简介
一、Boosting算法的发展历史
Boosting算法是一种把若干个分类器整合为一个分类器的方法,在boosting算法产生之前,还出现过两种比较重要的将多个分类器整合为一个分类器的方法,即boostrapping方法和bagging方法。我们先简要介绍一下bootstrapping方法和bagging方法。
1)bootstrapping方法的主要过程
主要步骤:
i)重复地从一个样本集合D中采样n个样本
ii)针对每次采样的子样本集,进行统计学习,获得假设Hi
iii)将若干个假设进行组合,形成最终的假设Hfinal
iv)将最终的假设用于具体的分类任务
2)bagging方法的主要过程
主要思路:
i)训练分类器
从整体样本集合中,抽样n* < N个样本 针对抽样的集合训练分类器Ci
ii)分类器进行投票,最终的结果是分类器投票的优胜结果
但是,上述这两种方法,都只是将分类器进行简单的组合,实际上,并没有发挥出分类器组合的威力来。直到1989年,Yoav Freund与 Robert Schapire提出了一种可行的将弱分类器组合为强分类器的方法。并由此而获得了2003年的哥德尔奖(Godel price)。
Schapire还提出了一种早期的boosting算法,其主要过程如下:
i)从样本整体集合D中,不放回的随机抽样n1 < n 个样本,得到集合 D1
训练弱分类器C1
ii)从样本整体集合D中,抽取 n2 < n 个样本,其中合并进一半被 C1 分类错误的样本。得到样本集合 D2
训练弱分类器C2
iii)抽取D样本集合中,C1 和 C2 分类不一致样本,组成D3
训练弱分类器C3
iv)用三个分类器做投票,得到最后分类结果
到了1995年,Freund and schapire提出了现在的adaboost算法,其主要框架可以描述为:
i)循环迭代多次
更新样本分布
寻找当前分布下的最优弱分类器
计算弱分类器误差率
ii)聚合多次训练的弱分类器
在下图中可以看到完整的adaboost算法:

现在,boost算法有了很大的发展,出现了很多的其他boost算法,例如:logitboost算法,gentleboost算法等等。在这次报告中,我们将着重介绍adaboost算法的过程和特性。
二、Adaboost算法及分析
从图1.1中,我们可以看到adaboost的一个详细的算法过程。Adaboost是一种比较有特点的算法,可以总结如下:
1)每次迭代改变的是样本的分布,而不是重复采样(re weight)
2)样本分布的改变取决于样本是否被正确分类
总是分类正确的样本权值低
总是分类错误的样本权值高(通常是边界附近的样本)
3)最终的结果是弱分类器的加权组合
权值表示该弱分类器的性能
简单来说,Adaboost有很多优点:
1)adaboost是一种有很高精度的分类器
2)可以使用各种方法构建子分类器,adaboost算法提供的是框架
3)当使用简单分类器时,计算出的结果是可以理解的。而且弱分类器构造极其简单
4)简单,不用做特征筛选
5)不用担心overfitting!
总之:adaboost是简单,有效。
下面我们举一个简单的例子来看看adaboost的实现过程:

图中,“+”和“-”分别表示两种类别,在这个过程中,我们使用水平或者垂直的直线作为分类器,来进行分类。
第一步:

根据分类的正确率,得到一个新的样本分布D2,一个子分类器h1
其中划圈的样本表示被分错的。在右边的途中,比较大的“+”表示对该样本做了加权。
第二步:

根据分类的正确率,得到一个新的样本分布D3,一个子分类器h2
第三步:
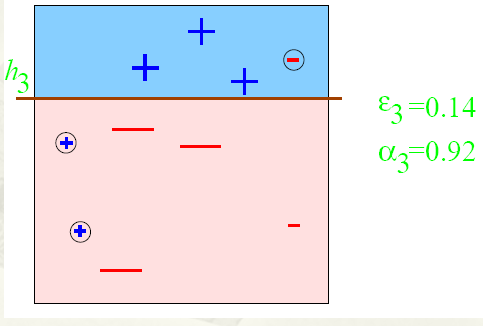
得到一个子分类器h3
整合所有子分类器:
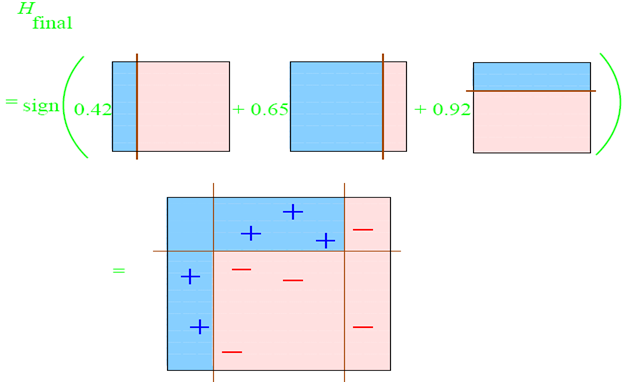
因此可以得到整合的结果,从结果中看,及时简单的分类器,组合起来也能获得很好的分类效果,在例子中所有的。
Adaboost算法的某些特性是非常好的,在我们的报告中,主要介绍adaboost的两个特性。一是训练的错误率上界,随着迭代次数的增加,会逐渐下降;二是adaboost算法即使训练次数很多,也不会出现过拟合的问题。
下面主要通过证明过程和图表来描述这两个特性:
1)错误率上界下降的特性
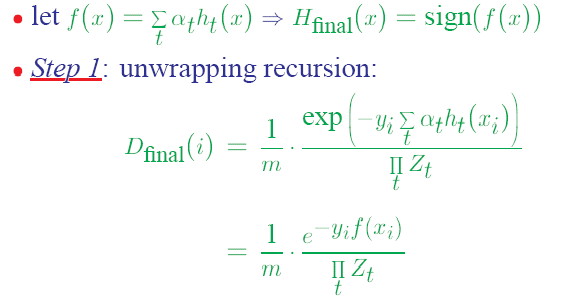


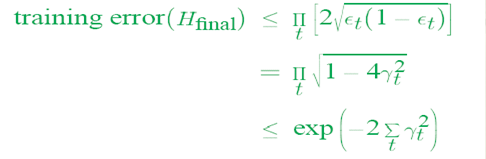
从而可以看出,随着迭代次数的增加,实际上错误率上界在下降。
2)不会出现过拟合现象
通常,过拟合现象指的是下图描述的这种现象,即随着模型训练误差的下降,实际上,模型的泛化误差(测试误差)在上升。横轴表示迭代的次数,纵轴表示训练误差的值。
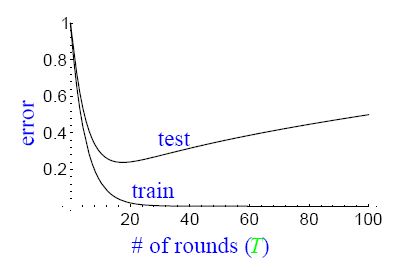
而实际上,并没有观察到adaboost算法出现这样的情况,即当训练误差小到一定程度以后,继续训练,返回误差仍然不会增加。
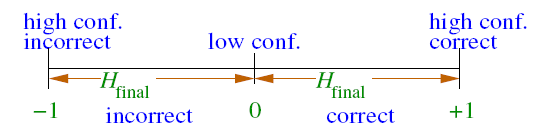
对这种现象的解释,要借助margin的概念,其中margin表示如下:
通过引入margin的概念,我们可以观察到下图所出现的现象:
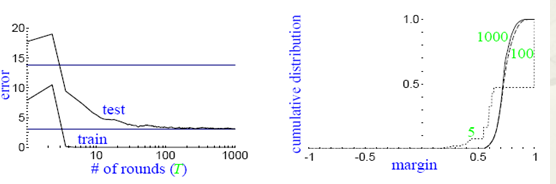
从图上左边的子图可以看到,随着训练次数的增加,test的误差率并没有升高,同时对应着右边的子图可以看到,随着训练次数的增加,margin一直在增加。这就是说,在训练误差下降到一定程度以后,更多的训练,会增加分类器的分类margin,这个过程也能够防止测试误差的上升。
三、多分类adaboost
在日常任务中,我们通常需要去解决多分类的问题。而前面的介绍中,adaboost算法只能适用于二分类的情况。因此,在这一小节中,我们着重介绍如何将adaboost算法调整到适合处理多分类任务的方法。
目前有三种比较常用的将二分类adaboost方法。
1、adaboost M1方法
主要思路: adaboost组合的若干个弱分类器本身就是多分类的分类器。
在训练的时候,样本权重空间的计算方法,仍然为:

在解码的时候,选择一个最有可能的分类
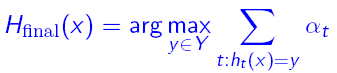
2、adaboost MH方法
主要思路: 组合的弱分类器仍然是二分类的分类器,将分类label和分类样例组合,生成N个样本,在这个新的样本空间上训练分类器。
可以用下图来表示其原理:
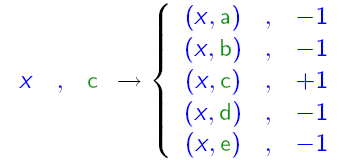
3、对多分类输出进行二进制编码
主要思路:对N个label进行二进制编码,例如用m位二进制数表示一个label。然后训练m个二分类分类器,在解码时生成m位的二进制数。从而对应到一个label上。
四、总结
最后,我们可以总结下adaboost算法的一些实际可以使用的场景:
1)用于二分类或多分类的应用场景
2)用于做分类任务的baseline
无脑化,简单,不会overfitting,不用调分类器
3)用于特征选择(feature selection)
4)Boosting框架用于对badcase的修正
只需要增加新的分类器,不需要变动原有分类器
由于adaboost算法是一种实现简单,应用也很简单的算法。Adaboost算法通过组合弱分类器而得到强分类器,同时具有分类错误率上界随着训练增加而稳定下降,不会过拟合等的性质,应该说是一种很适合于在各种分类场景下应用的算法。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号