扩散模型 - 简介、DDPM
扩散模型
1 扩散模型(DM)
扩散模型(Diffusion Model)起源于非均衡热动力学(non-equilibrium thermodynamics),是一类基于概率似然(likelihood)的生成模型。
当前对扩散模型的研究主要围绕三种主流的实现:
- 去噪扩散概率模型(Denoising Diffusion Probabilistic Models / DDPMs)
- 基于分数的生成模型(Score-based Generative Models / SGMs)
- 随机微分方程(Stochastic Differential Equations / Score SDEs)
当前最流行的扩散模型包括:
| 模型 | 文章 | 是否开源 | 开发 |
|---|---|---|---|
| DALL-E 2 | Hierarchical Text-Conditional Image Generation with CLIP Latents - arXiv 2022 | 否 | OpenAI |
| Imagen | Imagen: Text-to-Image Diffusion Model with Conditional Priors - arXiv 2022 | 否 | Google Research, Brain Team |
| Stable Diffusion | High-Resolution Image Synthesis with Latent Diffusion Models - CVPR 2022 | 是 | Stability AI |
1.1 生成模型之间的差异和关联
1.1.1 差异
| 模型 | 文章 | 优势 | 劣势 |
|---|---|---|---|
| 生成对抗网络 (Generative Adversarial Networks / GAN) | Generative Adversarial Networks - NIPS 2014 | - 高质量图像生成 - 无监督训练 - 相对较快的训练和推断 | - 训练过程不稳定 - 生成样本的多样性相对弱 |
| 变分自编码器 (Variational Autoencoders / VAE) | Auto-Encoding Variational Bayes - ICLR 2014 | - 准确捕获数据分布 - 计算过程可追踪 | - 生成质量不如 GAN - 表示能力有限 |
| 自回归模型 (Autoaggressive Model / AG) | Language Models are Unsupervised Multitask Learners - NeurlPS 2019 | - 长距离依赖 - 准确的概率估计 | - 训练和计算速度相对较慢 - 难以获取高维数据的全局依赖 |
| 流模型 (Flow-based Model) | Density Estimation Using Real NVP - ICLR 2017 | - 准确捕获数据分布 - 生成高质量细节的图像 | - 训练和计算速度相对较慢 - 架构设计比较困难 |
| 扩散模型 (Diffusion Model) | Denoising Diffusion Probabilistic Models - NeurlPS 2020 | - 高质量图像生成 - 准确捕获数据分布 - 训练过程固定 | - 训练和计算速度慢 |
其中,GANs 有着较好的图像质量--多样性的权衡(trade-off),导致生成高质量的图像的代价是牺牲一部分数据分布(多样性)。VAE、AG 和 Flow 在数据分布的学习能力方面优于 GAN,但是在图像质量上难以与之相比。此外,VAE 依赖与 surrogate loss、Flow 模型必须使用独特的架构来构建反向变换。
1.1.2 关联
GAN 与扩散模型的关联
GAN 训练过程不稳定的主要原因是生成数据和输入数据之间不重叠的数据分布。其中一种解决方法是通过给辨别器的输入注入噪音来进一步帮助生成器和辨别器的分布,这种方法由扩散模型所启发。另一方面,扩散模型的抽样速度要慢于 GAN,主要原因是去噪步骤中的高斯假设,该假设使得去噪的步长(step)较小。有工作通过使用 conditional GAN 来对每一步去噪过程建模,增大了去噪的步长。
VAE 与扩散模型的关联
DDPM 可被视为是固定编码器的层级式马尔可夫 VAE。具体来说,DDPM 的前向过程作为编码器,该过程可以用线性高斯模型描述。DDPM 的反向过程对应于解码器,在多个解码过程中共享。解码器中的潜变量和样本数据有着同样大小的尺寸。
有工作指出:在连续时间设定下,分数匹配目标函数可近似于深层 VAE 的证据下界(ELBO)。因此,扩散模型的优化过程可被视为训练一个无限层深的 VAE。
基于分数的潜生成模型(LSGM)进一步表示:在潜空间情境下,ELBO 可以作为特殊的分数匹配目标函数。
2 去噪扩散概率模型 (DDPM)
2.1 DDPM 总览
常规的深度学习模型通常用图表来表示网络结构,而扩散模型用数学公式来表述。
与常规的机器学习 Pipeline 做类比,扩散模型可以这样理解:
- 扩散模型的输入是原始图像或者文本 prompt,输出是类似原始图像的生成图像
- 扩散模型的训练包括两个过程:前向过程也叫扩散过程,反向过程也叫抽样过程。这两个过程都采用马尔科夫链
- 马尔科夫链包括一系列的状态和一系列的变化概率,这里的状态指的是含有不同的噪音等级的图片,变化概率指的是从当前状态变化到下一状态的概率,使用变化矩阵来实现
- 扩散模型的超参数包括:噪音的策略,学习率,迭代的次数等
- 扩散模型的损失函数优化的是负对数似然(negative log likelihood)
DDPM("Denoising Diffusion Probabilistic Models") 一文中给出的算法流程:

- 算法 1 描述的是训练过程(对噪音辨别器的训练)(前向过程、扩散过程)
- 重复如下步骤,直到收敛
- 从训练集的数据分布中抽取一个样本(图片)X0
- 在有限时间序列从 1 - T 的某个时刻 t
- 从高斯分布的噪音等级中选取某个等级的噪音 ε
- 对图片添加噪音
- 根据 loss 函数,开始梯度下降更新模型参数
- 重复如下步骤,直到收敛
- 算法 2 描述的是是反向过程(去噪过程、抽样过程)
- 从高斯分布中抽取某个图片 XT
- 对时间序列从 T 开始到 1,执行下述步骤:
- 如果 t > 1,从高斯分布中选取 z,否则 z = 0 (z 是使用重参数化reparameterization 技巧产生的表示法)
- 使用重参数化技巧计算 Xt-1
- 得到生成图片 X0 返回
2.2 前向过程
简单来说,前向过程的输入是原始图片,该图片服从一定的分布,输出是噪音图片,该图片服从高斯分布。
在前向过程中,对于一个输入图片,在某一个特定的时间 t 下,添加某种程度的噪音,得到噪音样本。前向过程不断重复该步骤,结果是一个时间序列和一系列噪音增大的图片。
具体来说,从数据分布 q(x) 中选取图片 x0,在时间序列 {0, T} 内的某个时间 t,选取某个等级的噪音 nt,把噪音添加到输入图片,得到噪音样本 xt。在 T 个步长后得到样本序列:{X0, Xt}。步长由超参数方差机制 βt(0 - 1) 来控制。
前向过程的数学表示:
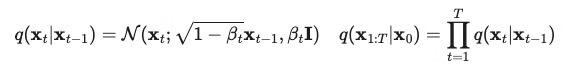
通过重参数化(reparameterization)技巧得到 αt = 1 - βt,因此上述过程可以化简为:
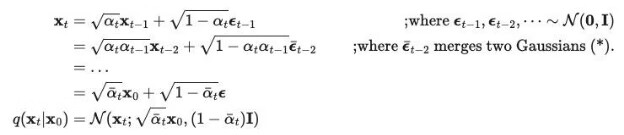
这样的好处是可以从任意一个时刻 t 以解析解(closed form)来抽样 xt。(把依赖于前一个时间的条件概率 q(xt|xt-1) 转化为依赖于初值的条件概率 q(xt|x0))
前向过程是固定的,也就是没有需要学习的参数。
2.3 反向过程
简单来说,反向过程的输入是添加了噪音的图片,该图片服从高斯分布。输出是去噪之后的图片,该图片服从一定的分布(如果网络训练完毕,那么该图片的分布应该接近模型的输入图片的分布)。
在反向过程中,对于一个带噪音的输入图片,在某一特定时间 t 下,消除一部分的噪音,得到噪音少了一些的图片。反向过程不断重复该步骤,结果是一个时间序列和一系列的噪音越来越少的图片,最终噪音完全消失,只剩下类似于原始图片的生成图片。
具体来说。如果可以逆转前向过程,那么只需要从最终的结果中抽样就可以得到清晰的图片。但是我们不能直接估计条件概率 q(xt-1|xt),因为这需要对整个数据集来执行前向过程。所以需要构建 pθ 来近似上述条件概率来运行反向过程。
反向过程的数学表示:
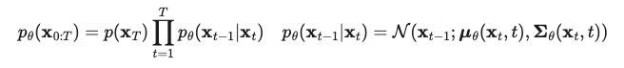
当条件为 X0 时,反向过程的条件概率是可以追踪的。
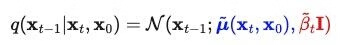
决定高斯分布的主要参数是:均值和方差。
在 DDPM("Denoising Diffusion Probabilistic Models") 一文中,作者固定了方差的大小,所以均值是反向过程中唯一需要学习的参数。(虽然后续 OpenAI 的工作表明,使方差变为学习参数能够提升 DDPM 的性能)。
使用贝叶斯公式和参数化技巧,可以把均值表示为:
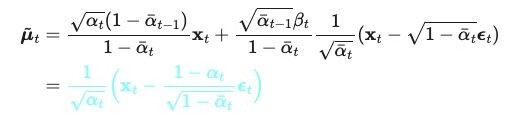
2.4 Loss 函数
由于扩散模型的学习过程非常类似于 VAE,所以我们可以用 VAE 中的变分下界(variational lower bound)或证据下界(evidence lower bound)来优化负对数似然)。
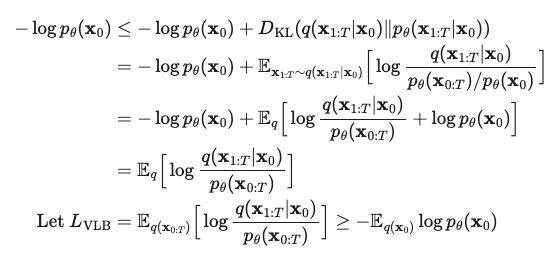
经过一系列推导可得:
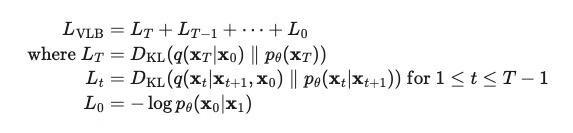
Lvlb 由三项损失组成:
- LT 是常数,因为 q 过程(前向过程)没有要学习的参数,而 pθ 过程(逆向过程)的 XT 就是该过程的输入或者前向过程的输出或者完全是噪音的图片,服从高斯分布。因此该项在计算时可以忽略
- Lt 用 KL 散度度量的生成数据和输入数据之间的分布差异
- L0 就是反向过程的分布
2.5 参数
2.5.1 超参数 βt
前向过程对噪音机制的方差 βt 设置为线性机制。变化范围从 β1 = 1e-4 到 βT = 0.02。实验结果表明:线性机制虽然能够生成高质量的图像,但是对数似然指标不如其他生成模型。
2.5.2 参数 Σθ
在 DDPM("Denoising Diffusion Probabilistic Models") 一文中,作者固定了 βt 作为常数,并设置 Σθ(xt, t) = σ^2I,其中 σ 是不可学习的,设置为 βt 或者 βt-hat。因为作者发现学习方差 Σθ 会导致训练过程不稳定并生成低质量图像。
参考
- Ling Yang et al. “Diffusion Models: A Comprehensive Survey of Methods and Applications .” arXiv 2023.
- Jonathan Ho et al. "Denoising Diffusion Probabilistic Models". NeurIPS 2020.
- Jiaming Song et al. "Denoising Diffusion Implicit Models". ICLR 2021.
- Alex Nichol et al. "Improved Denoising Diffusion Probabilistic Models". ICML 2021.
- Robin Rombach et al. "High-Resolution Image Synthesis with Latent Diffusion Models". arXiv 2022.
- Prafulla Dhariwal et al. Diffusion "Models Beat GANs on Image Synthesis". NeurIPS 2021.
- Jonathan Ho et al. "Classifier-Free Diffusion Guidance". NeurIPS Workshop 2021.
- Tim Salimans et al. "Progressive Distillation for Fast Sampling of Diffusion Models". ICLR 2022.
- Chenlin Meng et al. On Distillation of Guided Diffusion Models”. CVPR 2023.




