唯一分解定理 与 欧拉函数
算术基本定理,又称为正整数的唯一分解定理,即:每个大于1的自然数均可写为质数的积,而且这些素因子按大小排列之后,写法仅有一种方式。例如:
![]()
证明略(其实是我不懂我会乱说XD),如果需要证明就百度吧,上面有相关证明。
简而言之,唯一分解定理就是说任意一个大于1的自然数都可以写为几个素数的幂的乘积。记住这个就足够了(不困难嘛)。
在简单的了解了唯一分解定理后,思考一个问题,如何求小于等于n的自然数中与n互质的数的数量(好绕口),简单说就是,在[1,n]区间中与n互质的数有多少个(这下好多了),欧拉函数就是这个东西了,表示在[1,n]区间中与n互质的数的数量。既然我们前面讲了唯一分解定理,那么通过直觉可以证明(无视这句)欧拉函数与唯一分解定理有关。我们来考虑一个例子,对于整数n=360,将其分解得到
可知2,3,5都是360的素因子。在[1,360]这个区间中,2,3,5都是360的素因子,必然是360的约数,所以2的倍数,3的倍数,5的倍数都是360的约数,[1,360]中2的倍数有360/2个,3的倍数有360/3个,5的倍数有360/5,这些数都不可能与360互质,所以有=360-360/2-360/3-360/5。看上去是对的,但是很遗憾,360-360/2-360/3-360/5=-12,是一个明显不正确的负数,为什么会这样呢,我们考虑这样的几个数:6,10,15,6在作为2的倍数时已经减过一次了,但是作为3的倍数的时候又被减了一次,多减了一次,10也同样,作为2,5的倍数被减了两次,像这样的数一共有360/(2*3)+360/(2*5)+360/(3*5)个,为了体现公平公正的原则(无视这句),我们要将多减的这一次加回来,所以
=360-360/2-360/3-360/5 + 360/(2*3)+360/(2*5)+360/(3*5) = 108,这下结果是正数了,总应该对了吧,BUT(最讨厌但是了),来考虑一下30这个数,他在作为2,3,5的倍数的时候被减了3次,又在作为6,10,15的倍数的时候被加了三次,总结起来就是根本没把他算上嘛!为了体现公平公正的原则(够了!),我们要把他和他的倍数计算在内,即:
=360 -360/2-360/3-360/5 + 360/(2*3)+360/(2*5)+360/(3*5) –360/(2*3*5) = 96.终于正确了!
刚刚360只是3个质因子的幂的乘积,但是如果有更多的分解的质因子呢,当然就要反复的如上考虑了(不过会复杂一点),其实刚刚说了这么多,其实都是属于一个叫做容斥原理
的东西,感兴趣的可以自行百度,我在这里就不多赘述了。下面就不加证明的给出方程:
对于正整数的唯一分解式:
有
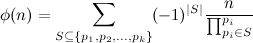
以上就是高大上的定义,但是如此高端的东西显得太平易近人了,虽然完全不明显,但是这个高大上的玩意儿是可以转化成
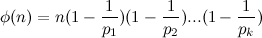
虽然中间的过程并不好理解,但是我们通过这一个简洁的式子是可以用感性的方法去理解的,对于任意一个素因子p,我们可以选着选他或者不选他,选的话就相当于选了-1/p作为展开式其中一项的因数,不选的话就相当于用1作为其中一项的因数(即没有影响)。
有了简化的公式,欧拉函数的程序实现就变得非常的简单了,注意我没有先生成n的唯一分解,而是边分解边计算结果,下面是代码
int euler_phi(int n)
{
int m=(int)sqrt(n+0.5);//n的素数范围在[1,sqrt(n)]之间
int ret=n;//初始化返回值
for(int i=2;i<=m;++i)if(!(n%i))//如果i是n的因子(可以保证是素因子)
{
ret=ret/i*(i-1);//计算结果
while(!(n%i))n/=i;//将i作为因子把n“除尽”
}
if(n>1)ret=ret/n*(n-1);//n可能也是质数
return ret;
}
如果要求1~n所有数的欧拉函数值,就需要用到类似于筛素数的思想了,给代码:
const int maxn=100+10;
int phi[maxn];//储存结果
void phi_table(int n)
{
memset(phi,0,sizeof(phi));
phi[1]=1;//首项为1
for(int i=1;i<=n;++i)if(!phi[i])//i必定为素数(类似筛素数法)
for(int j=i;j<=n;j+=i)//不断枚举i的倍数
{
if(!phi[j])phi[j]=j;//如果没有算过就初始化为j
phi[j]=phi[j]/i*(i-1);//进行计算
}
}


