拜占庭协议——236357byzantine generals

本文是236357Distributed Algorithms-The byzantine generals文档的总结。

本文阐述了拜占庭协议共识需要满足的条件、对拜占庭问题中的一些约束（如\(n>\frac{t}{3}\)）做了证明，有助于读者理解这些约束条件的产生、随后提出了一个满足拜占庭共识达成条件的协议。分别由净化协议（PP）与拜占庭协议（BG）（中译非官方）组成。
值得注意的是，本文提出的这个协议严重依赖于网络整体拓扑，由于每条路线都被记录，可能会造成更大的通信开销。且由于依赖拓扑结构，网络动态变化时，该协议可能无法很好发挥作用。
对于动态的区块链网络，很明显该协议并不适用。不过可以有一些启发，比如是否可以加入Purify的过程？是否有其他文章类似采用了类似Purify过程。答案肯定是有的。

fault VS Byzantine fault

一般来说，fault就是指一个replica在运行中因为各种原因发生了错误，无法参与接下来的消息交换。fault之后这个replica就退出消息传递过程。byzantine fault是指这个发生了错误的replica不仅不为系统安全性做贡献，反而恶意传递假消息来试图掌控系统中最后达成一致的value。
能忍受byzantine fault的系统一定可以忍受普通的crash，反之不成立。

两种协议

十字军协议（The Crusade Agreement）

达成十字军共识的条件是：

• 如果transmitter是可靠的，那么所有可靠的processor都应该就transmitter发送的值达成一致
• 如果transmitter是不可靠的，那么所有知道transmitter不可靠的processor都应该对同一个值达成一致（只要求是同一个值，并不指定具体的值）

拜占庭协议（The Byzantine Agreement）

达成拜占庭共识的条件是：

• 无论transmitter是否可靠，所有可靠的processor都应该就同一个值达成一致
• 如果transmitter可靠，可靠的processor们应该对transmitter发出的值达成一致

假设

1. 所有processor组成一个k-顶点连通图（k-connected bidirectional network）；——意味着任意去掉k-1个processor，也能保持联通；也意味着两个顶点之间至少有k个定点不相交。
2. 每一个processor都知道整个网络的拓扑结构；
3. processor们传递消息是通过连接（而非广播）传播；通过Link能捕捉到包吗，应该是（和xh确认了，是可以捕捉到的
4. 每一个processor都可以确定传给自己消息的邻居的身份；
5. 每一条消息都包含着自己的确定的传递路径；
6. 一个可靠的processor只会在看到这条消息的既定的传输路径中，自己将要发送给的邻居在自己之后，才会中继这条消息；
7. 一个可靠的processor只会在看到这条消息的既定传输路径中，自己在自己收到包的邻居之后，才会中继这条消息；——也就是说，一个faulty processor如果想把自己的消息传给可靠的processor，一定要在后继者的身份之前加上自己的identity；尽管接下来可能有新的faulty processor抹去了前一个faulty processor的identity，这个新的faulty processor的identity将会在消息路径中；——即，一个经过了faulty的，现在在可靠的processor手中的消息，消息路径中至少包含一个faulty的identity；
8. 可靠的processor收到消息后，不篡改、不窃听地将消息中继出去；
9. 可靠的processor传递消息时间有上界；
10. 系统中faulty processor数目有上界。

可疑的processor（Suspicious processors）

\(V_a={a_1,a_2,...,a_r}\)是某一个processor收到的所有的value。（这些value可能由于各种原因可能并不相等）。可疑的processor集合定义为\(U_x\)，其中不包括transmitter，如果去掉了\(V_a\)中经过了\(U_x\)中的所有的processor的value，那么\(V\)中所有的值都相同。

恶意节点的上限

Theorem 1：如果一个网络中的恶意节点不少于（大于等于）\(\frac{n}{3}\)，那么十字军一致不可能满足。

Lemma 1：如果一个包含三个网络节点的网络中有一个节点是faulty节点，那么该网络中不可能达到十字军一致。
Lemma 1 Proof：如图所示，其中处理器X是诚实的，而发送器T以及处理器Y未知是否诚实。该假设一定成立，因为在此网络中只有一个faulty节点，这意味着一定有一个处理器节点是诚实的。假设有一个有效的公式算法，能够达成十字军一致，那么这个协议应该在任何情况下都能满足十字军一致。

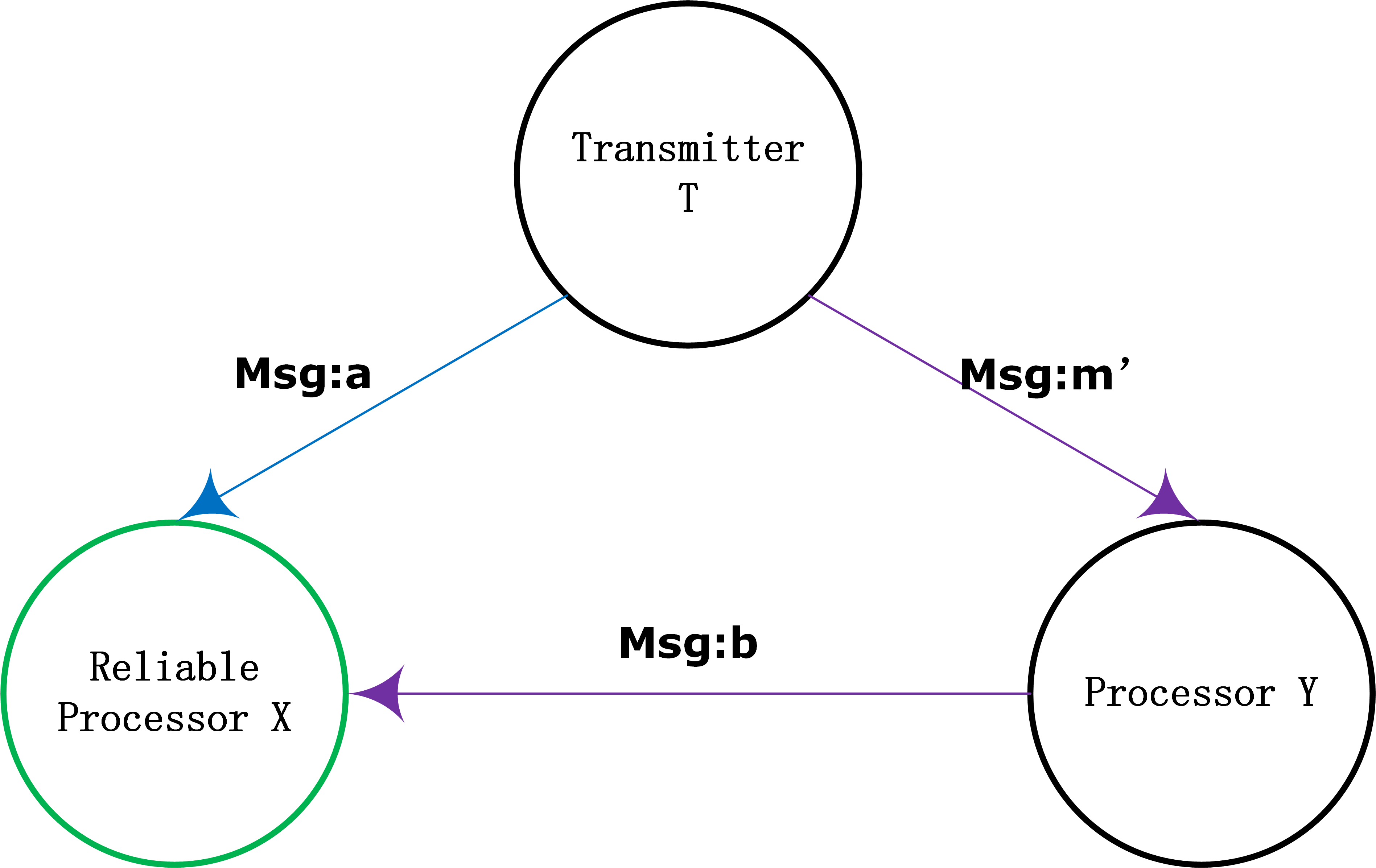
现在，T和Y中间一定有一个是恶意的。对X来说，它所能看到的只有自己收到的消息\([a:T,b:Y]\)，如果这个恶意节点干坏事了，那么\(a\neq b\)。
现在有两种情况：T是faulty或者Y是faulty。X清楚地知道某一个消息的传递路径，但是X无法通过路径来分辨究竟是T在发送消息的时候就作弊了，即\(a\neq m'\) && \(b=m'\)还是Y中途修改了T原本的消息，即\(a=m'\) && \(b\neq m'\)。因此X只能去猜谁是faulty。
从共识设计的角度而非实际情况的角度考虑：

• 如果X无条件选择T的值。因为如果T是可靠的，X必须接受T的值。
  • 如果T确实是可靠的，则Y不可靠。那么所有诚实的节点在transmitter诚实的时候都一致到transmitter的值√
  • 如果T不可靠，则Y可靠。那么X最终选择了\(a\)。而可靠的Y运行同样的共识算法，无条件选择T的值，此时Y选择了\(b\)，这违反了十字军一致的第二条。
  • 这样的策略不可行。
• 如果X无条件选择Y的值。
  • 如果Y确实可靠，则T不可靠。那么X发送给Y的\(a\)将会被Y选择，Y发送给X的\(b\)将会被X选择。这样，可靠的两个processor仍然选择了不同的值。这违反了十字军一致的第二条。
  • 如果Y不可靠，则T可靠。此时X选择了错误的\(b\)而非T发送的\(a\)，违反了十字军一致的第一条。
  • 这样的策略更不可行。
• 随机选择\(a\)或\(b\)。
  • 不用脑子就知道这个肯定不行。

归根究底，还是因为恶意节点给出的干扰信息超过了一定比例，导致诚实的节点无法根据网络中传递的信息来判断究竟哪个信息才是正确的信息。

现在使用Lemma1来证明Theorem1。
Theorem 1 proof：假设一个网络\(G\)中包含有t个恶意节点，且\(t\ge n/3\)。
我们证明了，如果存在一个有效的共识算法A使得网络\(G\)中能够达成十字军共识，那么也就意味着一定存在一个算法B可以在Lemma1所述网络中达成十字军共识。因为Lemma1说明了算法B不可能存在，因此算法A不可能存在。
现在我们把\(G\)中的节点分为三部分，每一部分\(\lceil n/3 \rceil\)。如果不为整，则可能会存在某个set少一两个。每一个set模拟lemma1中提到的T、X、Y。也就是说，由于\(t\ge n/3\)，每一个lemma1中的processor模拟不到t个\(G\)中的processor。
//剩下的证明有点奇怪...
如果模拟X的processors选择了X选择的内容，那么就等同于需要在Lemma1所述的情况下达成共识。这是不可能的。

Theorem 2：如果网络中的恶意节点不少于该网络连通性（network connectivity）的一半，则十字军共识不可能达成。
Theorem 2 Proof：假设某一个网络\(G\)连通性为k，且\(t\ge k/2\)。所有k个节点将网络分为三个部分，\(G_1\)、\(G_2\)、\(bottleneck\)，其中\(bottleneck\)是这k个瓶颈节点，在\(bottleneck\)中有至少\(k/2\)个恶意节点。如下图所示：

其中，\(G_1\)与\(G_2\)以及\(bottleneck\)分别连通，而\(G_1\)与\(G_2\)之间只能通过\(bottleneck\)连通，连通道路并不只有一条。这是可能的，因为假设\(G\)是一个k-顶点连通图。
如果在\(G_1\)中存在一个诚实的transmitter，它发送了值\(a\)，\(G_1\)中大部分可能选择\(a\)，但是反观\(G_2\)，它们至少会接收到\(k/2\)个\(b\neq a\)以及至多\(k/2\)个\(a\)，他们无法辨别出究竟哪个才是transmitter发出的那个值，不可能确定地选择transmitter给出的值。这违反了十字军一致的第一条。

注：ceil：\(\lceil e \rceil\)，取不小于表达式e的最小整数。如e=0.25，则取1。

净化算法（The Purifying Algorithm）

输入：\((t,a_1,a_2,...,a_r,x)\)，其中\(t\)时faulty的数目，\({a_1,...,a_r}\)是某一个正确节点收到的所有消息，\(x\)是这个节点。
算法过程：

如果 \(U_x\)存在，则净化后的值\(pv=value\)，\(value\)即为不经过\(U_x\)的消息确定的值。由\(U_x\)的定义，这个值是唯一的。
如果\(U_x\)不存在，则净化后的值不存在，\(pv=\emptyset\)。

Theorem 3：假设\(G\)是一个(2t+1)-顶点连通图网络，至多有t个恶意节点，如果一个诚实的transmitter将自己选择的值通过2t+1个不相交的路径传播出去，那么每一个诚实的processor节点都能收到transmitter的值。
Theorem 3 Proof：如果诚实的消息通过了2t+1个不相交的路径，也就是说t个恶意节点每个至多只能经过一条传输路径，这其中最坏的情况是，每一条传输路径中都只包含一个恶意节点，这样，有t条传输路径被恶意节点扰乱，可能产生错误的信息。但是仍然有t+1路径是诚实的，包含了transmitter原有的值。因此receiver可以辨别出哪个是诚实的transmitter发送的值，并同意这个值。
另外，由于每一个被恶意节点扰乱的路径都至少包含一个恶意节点的信息，因此可以通过\(U_x\)找出所有未被恶意节点扰乱过的信息。

Remarks 1：如果transmitter是恶意的，那么仅凭净化算法不能使所有诚实的processor达成共识的。

恶意的transmitter

定义：如果一个processor无法找到可能可疑的t个processors集合\(U_x\)，那么这个processor知道（explicit knows），transmitter是恶意的。

Lemma 2：如果恶意的processor最多只有t个，只有transmitter确实是faulty的时候，一个processor才会知道transmitter是faulty的。
Lemma 2 Proof：根据定义，只有一个processor找不到\(U_x\)的时候，他才会知道transmitter是faulty的。但是我们已经知道，如果transmitter是诚实的，那么根据净化算法一定能够找出\(U_x\)。

十字军算法 （CR Algorithm）

输入：\(\bold{CR}(G,z,V,t)\)，其中\(G\)是网络拓扑图，\(V\)是所有网络节点，\(z\)是transmitter，\(t\)是网络中存在的恶意节点的上限。
算法过程：

1. transmitter z通过\(2t+1\)条不相交的路径向每一个receiver发送自己的消息。(偏个题，这个communication开销挺大哈？)
2. 每一个receiver \(u\in V\)运行净化算法，得到自己接受的那个值\(a_u\)
3. u把自己拿到的值通过\(2t+1\)个不相交路径发送给\(V\setminus\{u\}\)
4. 假设\(M_u\)是u在步骤2、3中收到的所有的消息值，\(\emptyset\)代表在步骤3中miss掉的消息值。每一个receiver都能根据\(M_u\)在\(V\setminus\{z\}\)中找到\(U_x\)，以及那个自己接受的值。如果找不到这样的\(U_x\)，那么transmitter是恶意的，大家都选择value：\(faulty transmitter\)。

Theorem 4：算法\(CR\)可以在一个恶意节点\(t\le n/3\)，且连通性\(c\ge 2t+1\)的网络中达成十字军共识。
Theorem 4 Proof：假设两个诚实的processor \(x\)和\(y\)分别找到了可疑的processor集合\(U_x\)以及\(U_y\)，假设实际上\(T\)是恶意节点的集合，则：\(|T|,|U_x|,|U_y|\le t\)，则一定存在一个节点不在所有的这三个集合中，假设该节点为\(w\)。
由于\(w\)不在\(T\)中，那么\(w\)实际上是一个诚实的节点。而且由于连通性至少为\(2t+1\)，一定存在一条路不经过\(U_x\)和\(T\)，从\(w\)到达\(x\)。存在一条路不经过\(U_y\)和\(T\)，从\(w\)到达\(y\)。
这样\(x\)接收到的\(a(w)=a_w\)并且选择这个值，同样的，\(y\)接收到的\(a(w)=a_w\)并且选择这个值。因此\(x\)与\(y\)接受同一个值。（？为啥都会选择这个值？因为不在\(U_x\)和\(U_y\)中吗？
如果transmitter是可靠的，那么每一个可靠的processor都能接收到这个诚实的值，而不会得出结论“transmitter faulty”（根据Lemma 2），当然，他们同意接收器的值，因为z就是上述的w。

拜占庭算法（BG Algorithm）

输入：\(BG{G,v,U,t,m}\)，其中\(G\)是整个网络的拓扑图，\(U\)是节点们的子集，\(v\)是transmitter，\(t\)是faulty的数量，\(m\)是一个整型参数。
算法过程：

1. \(v\)向\(U\)中的所有节点发送消息，通过\(2t+1\)条disjoint path
2. 每个节点都运行净化算法，净化收到的消息，假设净化后的值为\(a_u\)，其中\(u\)为这个节点
3. 如果\(m>0\)，则继续运行下面的：
   (a. \(u\)作为transmitter，运行\(BG(G,u,U\setminus{u},t,m-1)\)，发出的消息是\(a_u\)
   (b. 对任意\(U\)中不包括\(u\)的节点\(w\)，使用\(a_w(u)\)表示他收到的上一步中\(u\)发出的消息的值，\(w\)将使用它们确定\(z\)的值，\(z\)是下一集合中大多数的值：\(z=majority({a_w(u)|x \in U})\)

Lemma 3：\(G\)为一个网络，\(U\)是一个包含基数至少为\(2r+m\)、恶意节点至多\(r\)个的\(G\)的子集，假设\(v\)是不在\(U\)中的一个processor，那么算法\(\bold{BG}(G,v,U,t,m)\)关于\(U\)满足拜占庭一致的第二条要求：transmitter reliable时。
Lemma 3 Proof：在transmitter诚实的情况下，对m进行归纳。

• \(m=0\)时：根据定理3。一共至少\(1+2r+m=2r+1\)个节点，其中最多\(r\)个恶意节点。当transmitter reliable的时候，通过\(2r+1\)个不相交路径发送自己的值，诚实节点一定能一致到transmitter的值。
• 假如\(m-1\ge 0\)的时候成立。根据定理3，诚实的transmitter把自己的值经过\(2r+1\)个不相交路径发送给所有\(U\)中的节点，则每一个\(U\)中的节点都能确认拿到这个正确的值。每一个receiver u都执行算法\(BG(G,u,U\setminus\{u\},t,m-1)\)，由于\(U\)包含至少\(2r+m\)个节点，那么\(U\setminus\{u\}\)包含\(2r+m-1\)个节点。通过归纳，每一个\(U\)中的诚实的节点都能确认收到同为\(U\)中诚实节点发出的诚实的值，假设为\(a\)。大多数receiver接收到\(2r+m\)个值，其中有一个值是本receiver自己发出的值。由于\(m> 0\)，且至多\(r\)个恶意节点，则拿到的正确值\(a\)一定占大多数。
  //诚实节点变多，为啥会不成立呢？

Theorem 5：\(G\)为一个网络，\(U\)是一个包含基数至少为\(3m\)的\(G\)的子集，假设\(v\)是不在\(U\)中的一个processor，如果\(U\setminus\{v\}\)包含至多\(m\)个faulty processors，那么算法\(\bold{BG}(G,v,U,t,m)\)关于\(U\)满足拜占庭一致的两个条件。
Theorem 5 Proof：对m进行归纳。

• \(m=0\)时：此时没有恶意节点在\(U\setminus\{v\}\)（接收者集合）中，根据定理3。
• 假如\(m-1\ge 0\)的时候成立。
  • 如果\(v\)诚实，那么根据Lemma 3。
  • 如果\(v\)不诚实，那么\(U\setminus\{u\}\)（其中\(u\)是一个接收者）中包含至少\(3m-1\)个processor，其中至多\(m-1\)个恶意节点（？），少于\(1/3\)的总节点个数。如果\(u\)诚实，那么所有的\(U\setminus\{u\}\)会一致到同一个值（3a，根据Lemma 3），如果\(u\)不诚实，他们会一致到某一个值，于是，每一个可靠的processor在3b在同一个set上计算大多数值，最终得到同样的值。

Theorem 5 Proof原文：

Corollary 1（推论）：如果一个有n个节点的网络\(G\)中恶意节点\(t< n/3\)且连通性\(c\ge 2t+1\)，那么算法\(BG\)满足拜占庭共识的要求。

参考文献