如何从零了解GCN
以下资源来源于: ①Kipf, Thomas N., and Max Welling. “Semi-supervised classification with graph convolutional networks.”
② https://blog.csdn.net/yyl424525/article/details/100058264
③知乎:https://www.zhihu.com/question/54504471 (如何理解GCN?)
写在前面
这段时间看了挺多GCN的资料,一开始就是拉普拉斯矩阵,特征分解,傅里叶变换,时域、频域,头都是大的,真的太复杂了,各种公式推导,证明。
然后看了知乎一个答主写的,不说证明,就说推导和演变,和一个答主用一个实例来说明公式的演变,感觉摸到那么点门槛了,昨天下午还在公司做了汇报,我讲了25分钟,被同事和上司逮着问了一个多小时,收获还是有的,就是太刺激了。
以下的内容是我在公司汇报的PPT上修改,加上完善写的,真正GCN我还只是看到了冰山一角,要是稍微了解一下可以看,如果要深入研究还是的去看公式的推演和证明。
预备知识
CNN中的卷积本质上是利用一个共享参数的过滤器(kernel),通过计算中心像素点以及相邻像素点的加权和来构成feature map实现空间特征的提取,加权系数就是卷积核的权重系数。 那么卷积核的系数如何确定呢?首先随机初始化,然后根据loss函数通过反向传播梯度下降进行迭代优化。卷积核的参数通过优化求出才能实现特征提取的作业,GCN的理论很大一部分工作就是引入可以优化的卷积参数。
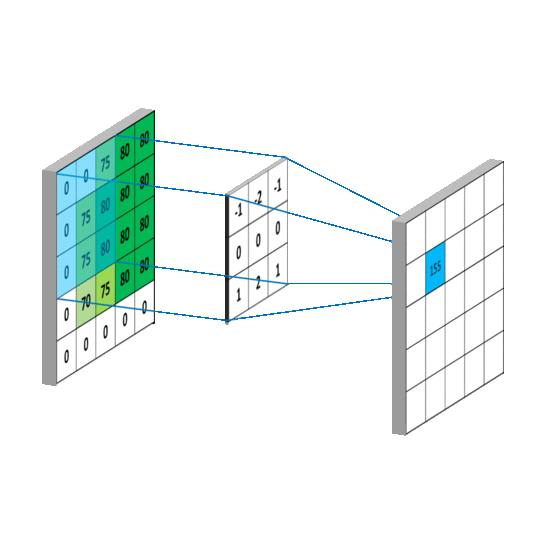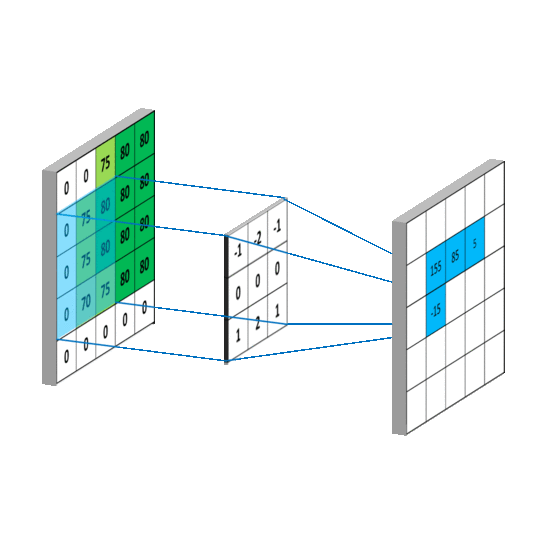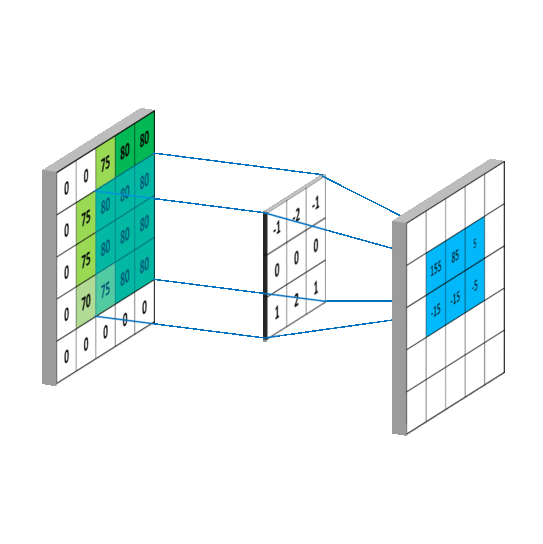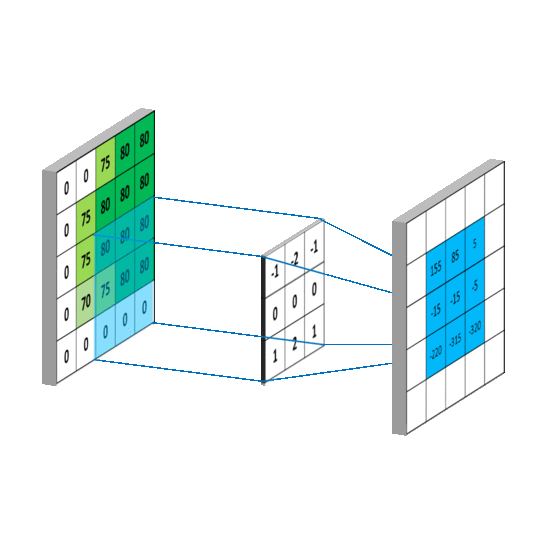
拉普拉斯矩阵(Laplacian matrix) 也叫做导纳矩阵、基尔霍夫矩阵或离散拉普拉斯算子,主要应用在图论中,作为一个图的矩阵表示。对于图 G=(V,E),其Laplacian 矩阵的定义为 L=D-A,其中 L 是Laplacian 矩阵, D=diag(d)是顶点的度矩阵(对角矩阵),d=rowSum(A),对角线上元素依次为各个顶点的度, A 是图的邻接矩阵。度矩阵D可以又邻接矩阵A计算得来,以下有用到。
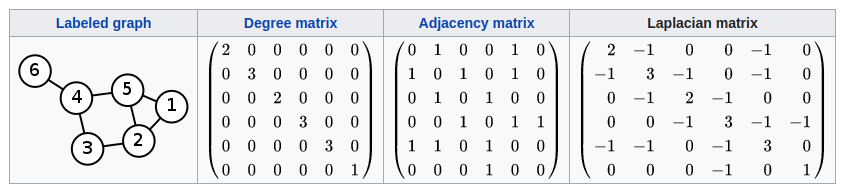
普通形式的拉普拉斯矩阵: L=D−A
对称归一化的拉普拉斯矩阵(Symmetric normalized Laplacian):
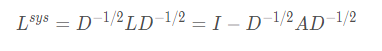
随机游走归一化拉普拉斯矩阵(Random walk normalized Laplacian):
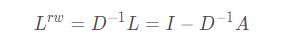
这里只需要大概知道有这么个变形就行了,具体用处后面会说。
使用GCN的原因
CNN普通卷积神经网络研究的对象是具备Euclidean domains的数据,Euclidean domains data数据最显著的特征是他们具有规则的空间结构,如图片是规则的正方形,语音是规则的一维序列等,这些特征都可以用一维或二维的矩阵来表示,卷积神经网络处理起来比较高效。
生活中很多数据不具备规则的空间结构,称为Non Euclidean data,如,推荐系统、电子交易、分子结构等抽象出来的图谱。这些图谱中的每个节点连接不尽相同,有的节点有三个连接,有的节点只有一个连接,是不规则的结构。对于这些不规则的数据对象,普通卷积网络的效果不尽人意。CNN卷积操作配合pooling等在结构规则的图像等数据上效果显著,但是如果作者考虑非欧氏空间比如图(即graph,流形也是典型的非欧结构,这里作者只考虑图),就难以选取固定的卷积核来适应整个图的不规则性,如邻居节点数量的不确定和节点顺序的不确定。
图的结构一般来说是十分不规则的,可以认为是无限维的一种数据,所以它没有平移不变性。每一个节点的周围结构可能都是独一无二的,这种结构的数据,就让传统的CNN、RNN瞬间失效。
GCN的表示
这一章节也是只要了解一下GCN 的公式的样子,和公式中的字母代表什么,具体的演变后面再说。
假设我们手头有一批图数据,其中有N个节点(node),每个节点都有自己的特征,我们设这些节点的特征组成一个N×D维的矩阵X,然后各个节点之间的关系也会形成一个N×N维的矩阵A,也称为邻接矩阵(adjacency matrix)。X和A便是我们模型的输入。GCN也是一个神经网络层,它的层与层之间的传播方式是:
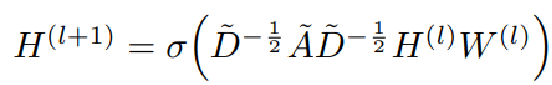
这个公式中: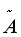 =A+I,I是单位矩阵 ,
=A+I,I是单位矩阵 ,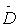 是
是 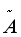 的度矩阵(degree matrix),公式为
的度矩阵(degree matrix),公式为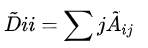
H是每一层的特征,对于输入层的话,H就是X, σ是非线性激活函数
l是指当前GCN的层数,当l=0 的时候,H0就是输入的特征矩阵X,所以上一层的输出 ,就是下一层的输入H。
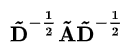 这个部分是可以直接算出来的,暂且不用知道为什么这么算。
这个部分是可以直接算出来的,暂且不用知道为什么这么算。
为了直观理解,我们用论文*中的一幅图:
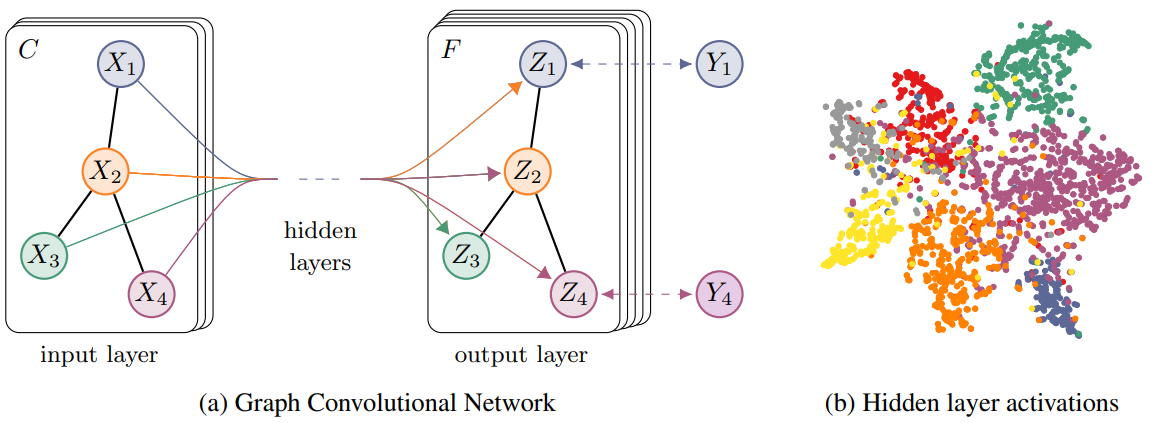
上图中的GCN输入一个图,通过若干层GCN每个node的特征从X变成了Z,但是,无论中间有多少层,node之间的连接关系,即A,都是共享的。
假设我们构造一个两层的GCN,激活函数分别采用ReLU和Softmax,则整体的正向传播的公式为:
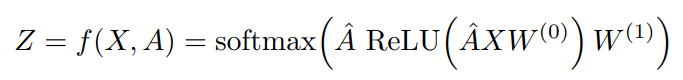
最后,我们针对所有带标签的节点计算cross entropy(交叉熵)损失函数:
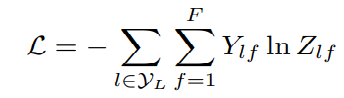
就可以训练一个node classification的模型了。由于即使只有很少的node有标签也能训练,作者称他们的方法为半监督分类。
GCN的演变(来源)
重点章节?
由简入繁的方法来解释GCN公式的演变
我们的每一层GCN的输入都是邻接矩阵A和node的特征H,那么我们直接做一个内积,再乘一个参数矩阵W(典型的卷积的方法),然后激活一下,就相当于一个简单的神经网络层。
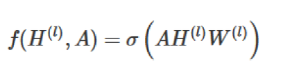
实验证明,即使就这么简单的神经网络层,就已经很强大了。
GCN使用的卷积为X'=AX,A是邻接矩阵。这其实是一个laplacian smoothing。这个平滑操作使邻接的节点的feature/latent point互相靠近,邻接的节点多是同类的,最终就使同类的feature/latent point聚在一起,提高了分类准确率。
但是这个简单模型有几个局限性:
只使用A的话,由于A的对角线上都是0,所以在和特征矩阵H相乘的时候,只会计算一个node的所有邻居的特征的加权和,该node自己的特征却被忽略了。因此,我们可以做一个小小的改动,给A加上一个单位矩阵I,这样就让对角线元素变成1了。
A是没有经过归一化的矩阵,这样与特征矩阵相乘会改变特征原本的分布,产生一些不可预测的问题。所以我们对A做一个标准化处理。首先让A的每一行加起来为1,我们可以乘以一个D-1 ,D就是度矩阵。我们可以进一步把 D-1 拆开与A相乘,得到一个对称且归一化的矩阵: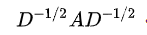 。
。
通过对上面两个局限的改进,我们便得到了最终的层特征传播公式:是不是感觉很简单?(大雾,其实从数学的角度来说从拉普拉斯矩阵和傅里叶变换来说,超级复杂,我自己也没搞清楚,这个推演来自知乎的答主@蝈蝈,感兴趣的可以从我最上方写的那个知乎去看看)
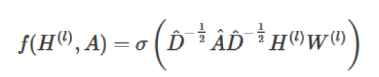
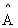 = A +I,
= A +I, 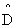 为
为 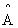 的度矩阵
的度矩阵
公式中的 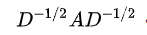 与对称归一化拉普拉斯矩阵十分类似,而在谱图卷积的核心就是使用对称归一化拉普拉斯矩阵,这也是GCN的卷积叫法的来历。
与对称归一化拉普拉斯矩阵十分类似,而在谱图卷积的核心就是使用对称归一化拉普拉斯矩阵,这也是GCN的卷积叫法的来历。
用实例来阐述公式的演变
下面用一个例子来说一下GCN公式的演变,同样来自知乎答主。
“你朋友圈的平均工资就是你的工资”,利用社交网络(graph)中的关联信息(edge),我们可以得到其他的有效信息(node represent)。
求和
假设我们要预测一个人Xi的工资,我们可以由跟他有关联的人的工资加权和。也就是下面这个式子。
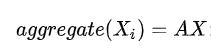
加权和
我们前面说到的邻接矩阵A,都是0,1构成的,有关联就是1,没有关联就是0。但是很多情况下的关联程度并不是一致的,也就是无向图也有可能是带权无向图,把邻接矩阵换成有权邻接矩阵也可以满足上式。
从求工资这个例子来说,我认识马云,马化腾也认识马云,但是马化腾更马云的关系肯定比我跟马云的关系好(没有引战 的意思),所以邻接矩阵的数不能一样,带权之后,我跟马云是1,那马化腾和马云就是1000000000。以此说明马云和马化腾的工资更相近。
添加自环
对于图来说,用周围点的特征乘以W矩阵来代表自己点,但是忽略了自己点的特征,因此把A换成A+I,使得邻接矩阵的对角线变成1,给每个点添加了一个自环,也就是说 自己和自己是有关联的。
从求工资这个实例来说,“我”可能比较会说话会讨好上司,所以升职加薪,但是对比周围工作能力想当的朋友,我的工资>他们,因此求工资的时候要加上自己的“特征”。
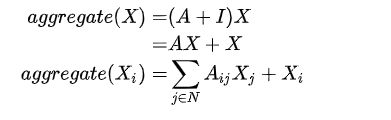
归一标准化
以上的操作都还只是加权和,没有算平均,为了不出现“因为朋友特别多=自己工资特别高”这个说法,我们一般求加权和平均,因此我们要把A矩阵中的每一行的和归一化成1,这里就用到我们前面说的D矩阵(度矩阵)了,D矩阵的对角线上的数字就是邻接矩阵每一行的和,要归一化就让A乘以一个D-1就使得D-1A得到一个每一行都为1的矩阵,达到了归一标准化的效果。
从实例上来说,假设一个朋友比较少的大佬,和一个工资比较低但是有关系的“朋友”特别多的交际花,如果不归一标准化,就会出现这个交际花的朋友工资和>这个大佬的很少的朋友的工资和,这种情况。
按理来说,度越小(邻居越少),分配的权重应该越大,也就是说,每个节点通过边对周围的点发送信息量相同,边越多,发送给周围的每一个点的信息就越少。
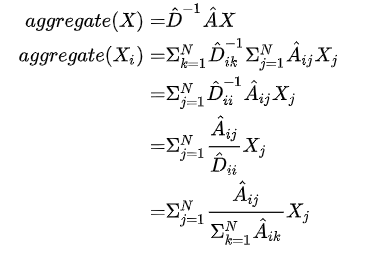
看到上式,你也许会想,这是乘以的D-1,还不是我们前面看到的D-0.5AD-0.5,为什么要把D-1拆开乘在两边呢,别急 我们下面说。
对称归一标准化
现在我们还是从实例来说,前面说了一个大佬朋友很少,这里我们做一个假设,大佬为i点,他只有2个朋友,一个也是大佬,另一个朋友是那个交际花呢?如果按上式的归一化,那大佬i的工资=0.5*另一个大佬的工资+0.5*交际花的工资?这大大不妥,这个交际花以一己之力把大佬的预测工资拉低了一半。因此我们在计算节点i的值的时候,也要考虑相连节点j的情况。
我们使用几何平均数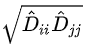
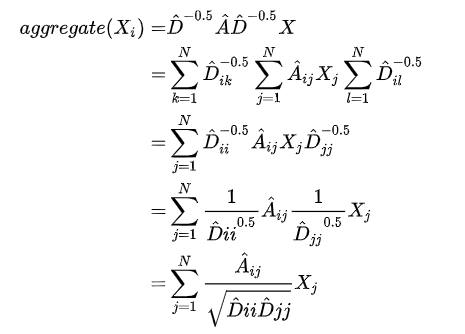
从上式看到,除以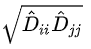 ,就等于乘以Dii-0.5*Djj-0.5,那么为什么分别乘在两边呢,是为了对称。(具体的推导可以看一下别的文章,有的大佬说是为了和归一化的拉普拉斯矩阵一致)
,就等于乘以Dii-0.5*Djj-0.5,那么为什么分别乘在两边呢,是为了对称。(具体的推导可以看一下别的文章,有的大佬说是为了和归一化的拉普拉斯矩阵一致)
以上我们就用一个例子推演出了GCN公式的演变。
GCN的优势
然后作者*做了一个实验,使用一个俱乐部会员的关系网络,使用随机初始化的GCN进行特征提取,得到各个node的embedding,然后可视化:
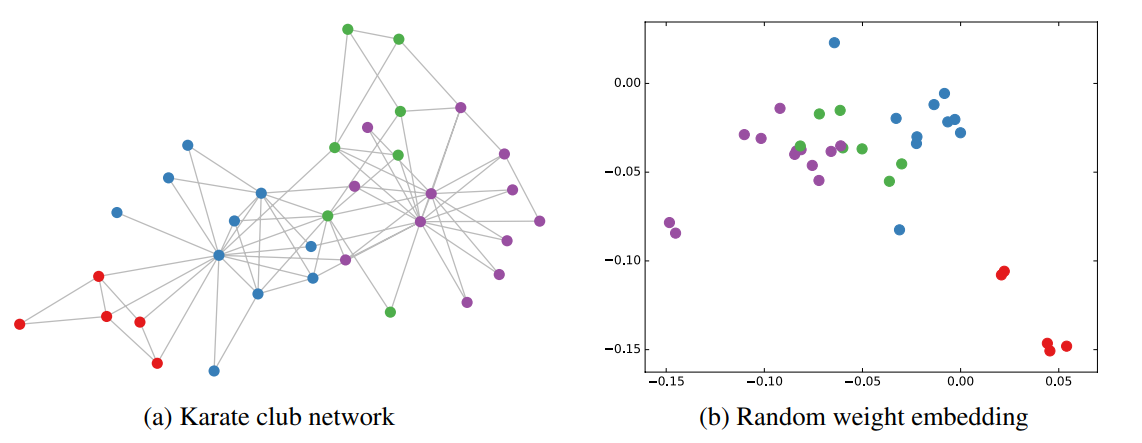
这里我解释一下,实验到这一步,是没有用任何有标签的数据,只给了一个邻接矩阵,如左图,没有给点的颜色,随机分配一个权重W,用GCN的公式算,没有训练就能得到右图的结果。
从步骤上说就是,输入一个邻接矩阵A,乘以一个随机初始化的矩阵W,不经过训练没有标签,没有loss反向转播,直接得到的Z,Z在空间上的分布就是没有颜色的上图,把点分布在空间上之后,回头再去看每个点的标签,发现同标签的点再空间上已经达到了聚类的效果,并且这个实验中,并没有点的特征矩阵X ,直接使用的单位矩阵I当做X 去输入,也就是A*I*W的效果。
可以发现,在原数据中同类别的node,经过GCN的提取出的embedding,已经在空间上自动聚类了。如果对比其他的网络,不用标签没有特征,随机化的权重矩阵W,根本得不到任何结果,所以说,单根据一个邻接矩阵已经颇有成效了。
(Kipf, Thomas N., and Max Welling. “Semi-supervised classification with graph convolutional networks.” )
作者接着给每一类的node,提供仅仅一个标注样本,然后去训练,得到的可视化效果如下:(也就是给每一种颜色的点中,给一个点颜色标签)
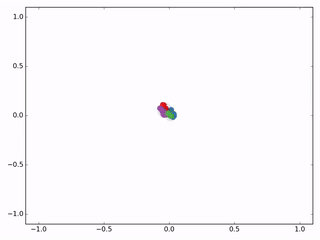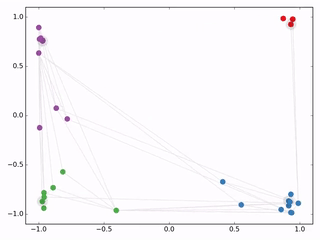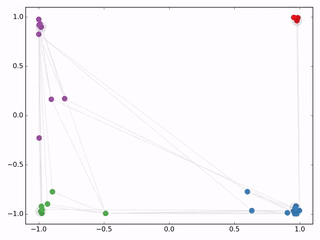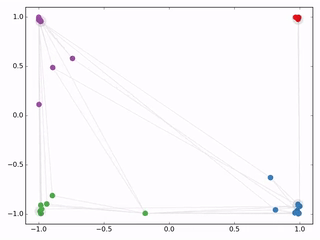
从上图可以看到,效果相当好,每种类型一个样本标签,因此作者称之为半监督,用很少的样本点就能训练出不错的效果。
GCN的优点
1)、权值共享,参数共享,从AXW可以看出每一个节点的参数矩阵都是W,权值共享;
2)、具有局部性Local Connectivity,也就是局部连接的,因为每次聚合的只是一阶邻居; 上述两个特征也是CNN中进行参数减少的核心思想。
3)、感受野正比于卷积层层数,第一层的节点只包含与直接相邻节点有关的信息,第二层以后,每个节点还包含相邻节点的相邻节点的信息,这样的话,参与运算的信息就会变多。层数越多,感受野越大,参与运算的信息量越充分。也就是说随着卷积层的增加,从远处邻居的信息也会逐渐聚集过来。
4)、复杂度大大降低,不用再计算拉普拉斯矩阵,特征分解
GCN的不足
1)、扩展性差:由于训练时需要需要知道关于训练节点、测试节点在内的所有节点的邻接矩阵A,因此是transductive的,不能处理大图,然而工程实践中几乎面临的都是大图问题,因此在扩展性问题上局限很大,为了解决transductive的的问题,GraphSAGE:Inductive Representation Learning on Large Graphs 被提出;
2)、局限于浅层:GCN论文中表明,目前GCN只局限于浅层,实验中使用2层GCN效果最好,为了加深,需要使用残差连接等trick,但是即使使用了这些trick,也只能勉强保存性能不下降,并没有提高,Deeper Insights into Graph Convolutional Networks for Semi-Supervised Learning一文也针对When GCNs Fail?这个问题进行了分析。
3)、不能处理有向图:理由很简单,推导过程中用到拉普拉斯矩阵的特征分解需要满足拉普拉斯矩阵是对称矩阵的条件;
GCN的应用
GCN,图卷积神经网络,实际上跟CNN的作用一样,就是一个特征提取器,只不过它的对象是图数据。GCN精妙地设计了一种从图数据中提取特征的方法,从而让我们可以使用这些特征去对图数据进行节点分类(node classification)、图分类(graph classification)、边预测(link prediction),还可以顺便得到图的嵌入表示(graph embedding)。
从前面GCN的优势有讲到,使用随机化的GCN 都已经起到了聚类的效果,那么使用训练过的GCN已经起到了很好的训练效果,把GCN结果当做embedding表示节点 。图边结构预测任务和图的分类问题都是基于graph embedding来做的。
具体应用场景: 文本分类 角色标注 翻译 关系抽取 事件抽取 知识图谱 (注:来自https://zhuanlan.zhihu.com/p/72546603?utm_source=wechat_session)
GCN的后续思考
关于带权图问题: GCN论文里的针对的是无权的无向图,并且采用的是平均聚合的方法,邻居之间没有权重。但是,现实生活中更多的是带权图。比如,我们都认识马化腾,但是张志东与马化腾的亲密度要比我们和马化腾的亲密度高得多。因此,可以预测张志东的工资比我们更接近马化腾。 不过GCN还是可以直接处理带权图,原来的邻居矩阵取值只能是0和1,现在可以取更多的权值。
关于有向图问题 前面的都是针对于无向图的问题,所有拉普拉斯矩阵是对称矩阵,但是在有向图中,就不能定义拉普拉斯矩阵了。目前的两种解决思路:
(a)要想保持理论上的完美,就需要重新定义图的邻接关系,保持对称性 比如这篇文章MotifNet: a motif-based Graph Convolutional Network for directed graphs 提出利用Graph Motifs定义图的邻接矩阵。
(b)有人认为基于空间域的GCNs都可以处理有向图,比如GraphSAGE、GAT等,聚合邻居信息时根据有向边判断是否是邻居即可
节点没有特征的图:对于很多网络,可能没有节点的特征,这个时候也是可以使用GCN的,如论文中作者对那个俱乐部网络,采用的方法就是用单位矩阵 I替换特征矩阵X,有的地方也用节点度作为节点特征。
GCN的实验(非典型!!!)
在事件类型分类(多标签)中,句子的embedding 放入双向lstm+attention中训练,样本的标签(事件类型)转化为embedding 加入到gcn中训练,得到事件之间共现的概率矩阵。
这两条线是并行的,gcn得到的结果+LSTM得到的结果,再去进行反向传播计算loss。
#随机初始化一个服从正态分布的n*n矩阵 ,无先验的监督学习 self.adj = nn.Parameter(torch.randn(hyper.n_class, hyper.n_class)) # 实例化GraphConvolution self.gc1 = GraphConvolution(self.hidden_dim, self.hidden_dim) self.gc2 = GraphConvolution(self.hidden_dim, self.hidden_dim) self.relu = nn.LeakyReLU(0.2)
为什么说我这里说的这个事件分类的实验是一个非典型的实验呢,前面我们说了邻接矩阵A是一个固定不变的输入,但是本实验中,我们并不知道事件之间的共现性是什么样子的,事件之间的关系是什么样子的,因此我们随机初始化了一个邻接矩阵A(adj),通过样本的标签,也就是事件标签,在不断的训练中,邻接矩阵A和权重矩阵W都在不断优化。老师说这个非典型的GCN的应用的局限性是我们的图,是一个不变的图。
我们的事件标签一共6种,首先我们假设这6种事件(节点)是全联通的,并且初始化了一个邻接矩阵A,当进入一个输入,假设是 AC,也就是说A事件和C事件在这个样本中同时出现了,那么AC的邻接矩阵对应的权重就加一点,以此不断优化邻接矩阵adj。
GCN定义的 forward函数
def forward(self, input, adj):
support = torch.matmul(input, self.weight) # X*W
output = torch.matmul(adj, support) # AXW
if self.bias is not None:
return output + self.bias
else:
return output
由于我们的邻接矩阵没有确定,也没有D,所以没有使用归一标准化的GCN公式。
训练结束后模型中邻接矩阵adj 的打印结果。
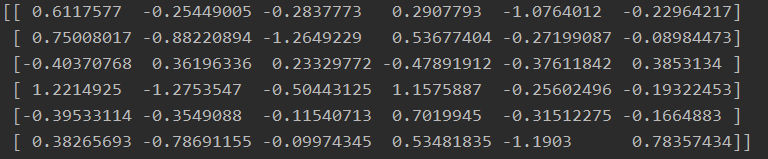
邻接矩阵灰度图:
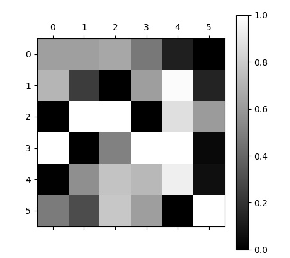
当时就有人问我,为什么邻接矩阵中会出现负数?
问的好我也不知道,老师给出的解释是,1 可能数据有噪音数据
2 负数的点,可能代表两个事件互斥
我另一个同事给出的原因是:深度学习的不可解释性(大雾),你要是能解释清楚,那你就NB了。
我后来想到的原因是 初始化A的时候就已经有负数了,然后优化的时候只加?
实验过后,确实初始化的时候有负数,但是在训练过程中也有增有减_(:з」∠)_
我现在把邻接矩阵初始化成单位矩阵,再做下实验。
改成单位矩阵后,13个epoch的adj:
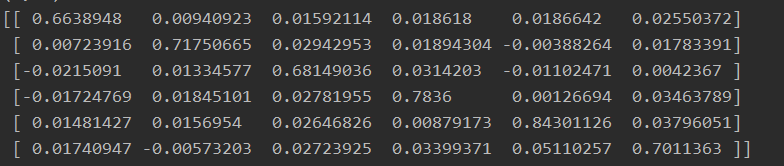
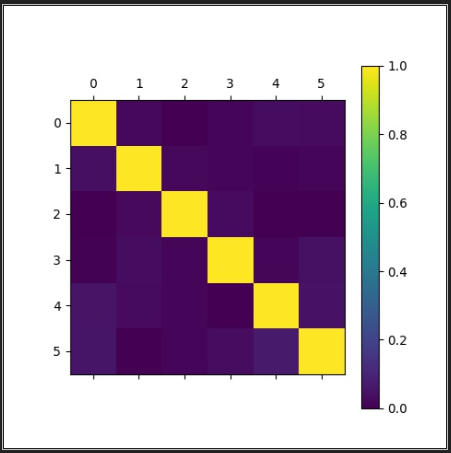
单位矩阵初始化的adj训练50个epoch 最好的结果的adj:
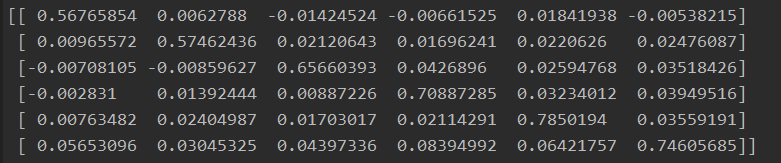
emmmm应该是我的数据中出现2个以上的标签的例子比较少。在ACE2005的数据上取得了比较好的效果,比不用GCN处理上升了2-3个百分点。
虽然是一个不太典型的实验,但是我觉得还是挺有启发性的,因为我觉得现实中的关系也就是邻接矩阵A不是那么好计算的,通过样本中标签一起出现来计算邻接矩阵也许是个不错的方法。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号