真实场景的虚拟视点合成（View Synthsis）详解

　　上一篇博客中介绍了从拍摄图像到获取视差图以及深度图的过程，现在开始介绍利用视差图或者深度图进行虚拟视点的合成。虚拟视点合成是指利用已知的参考相机拍摄的图像合成出参考相机之间的虚拟相机位置拍摄的图像，能够获取更多视角下的图片，在VR中应用前景很大。

　　视差图可以转换为深度图，深度图也可以转换为视差图。视差图反映的是同一个三维空间点在左、右两个相机上成像的差异，而深度图能够直接反映出三维空间点距离摄像机的距离，所以深度图相较于视差图在三维测量上更加直观和方便。

• 利用视差图合成虚拟视点
• 利用深度图合成虚拟视点

一、利用视差图合成虚拟视点

　　由于视差图反映的是三维空间点在左、右两个相机上成像的差异，并且由于提前进行了立体校正，这种差异就反映在图像的同一行上。在立体匹配的SGBM算法中就是以其中某一副为参考图像，在另一幅图像的同一行上搜索匹配点。因此在合成虚拟视点时也只需在同一行上平移虚拟摄像机位置即可。流程如下：

　　（1）. 假设视差图中某一个像素点的视差值为dmax，也就是说从左摄像机camL到右摄像机camR之间，该像素点的视差值变化范围为0~dmax。为了方便介绍我将其归一化到alpha取值范围为0~1。

　　（2）.那么如果我要获取alpha=0.5位置时候虚拟相机位置的图像呢，那么此时该像素点和左图像匹配点的坐标差异就是0.5 * dmax，和右图像匹配点的坐标差异也是0.5 * dmax；如果alpha=0.3，那么此时该像素点和左图像匹配点的坐标差异就是0.3 * dmax，和右图像匹配点的坐标差异也是0.7 * dmax；

　　（3）.根据上面提到的原理，显而易见，合成新视点时候只需要将左图像的像素点位置向右移动alpha *dmax，或者右图像的像素点向左移动(1-alpha)*dmax，就可以得到alpha位置处虚拟相机拍摄的虚拟视点图像。

　　合成虚拟视图即可以利用左参考图像和对应的左视差图，也可以利用右参考图像和对应的右视差图，更好的是都利用上得到两幅虚拟视点图像，然后做图像融合，比如基于距离的线性融合等。

　　

　　在算法的实现中，又有两种选择，一个是正向映射，一个是反向映射（逆向映射）。

　　1.正向映射

　　① 将原参考图像中整数像素点根据其对应上视差值平移到新视图上。

　　② 平移后像素点坐标可能不是整数，为了获取整数坐标，采用最近邻插值，将原图像像素值赋值到新坐标位置。

　　③ 由于最近邻插值会损失精度，因此在物体的边缘会出现锯齿效应。

　　2.反向映射

　　① 利用参考视点的视差图dispL，算出虚拟视点位置的视差图dispV;

　　② 由于遮挡等因素影响，dispV肯定会出现空洞和裂纹，所以需要做一个空洞填充holeFilling；

　　③ 利用dispV将虚拟视点图像中的整数坐标平移到参考视点位置下的坐标，此时也可能不是整数，而是浮点数坐标。这就面临一个从哪里取值的问题。

　　④ 取参考视点图像浮点数坐标附近4个点的像素值，用双线性插值算出对应虚拟视点图像位置处的像素值即可。

　　⑤ 由于双线性插值属于一种加权平均的思想，能够有效避免精度损失造成的锯齿现象，但是算法复杂度要高。

　　

　　下面给出利用左视点图像和对应视差图获取虚拟视点位置图像的效果(反向映射+双线性插值)：

　　　　不进行空洞填充

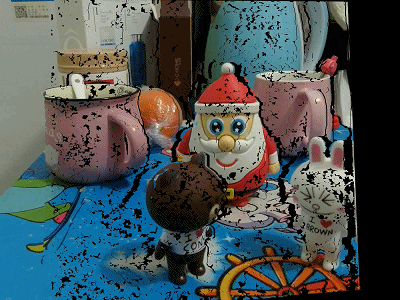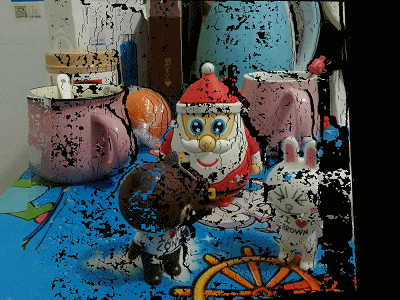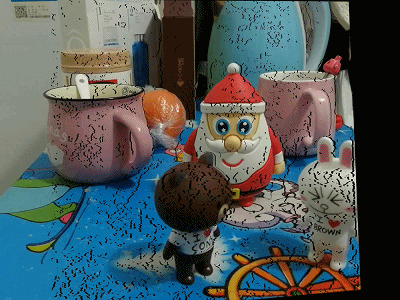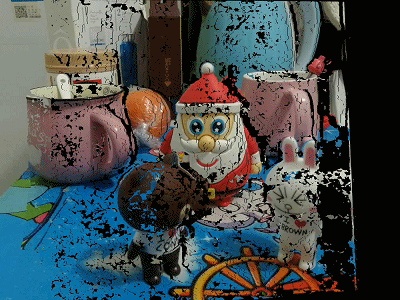
空洞填充

 

---

 

二、利用深度图合成虚拟视点

　　和利用视差图合成新视点一样，利用深度图合成新视点也有两种选择：1. 正向映射  2. 反向映射。由于正向映射比较简单并且效果不理想，因此目前大多采用反向映射方法。

　　已知内参矩阵K，下面仍然以左图像imgL和depthL为参考图像，获取alpha=0.5位置处的虚拟视点图像，简要步骤如下：

　　（1）. 利用内参矩阵K， 将depthL映射到三维空间点，平移到虚拟相机坐标下后，重投影到虚拟视点图像平面，得到虚拟视点位置处的深度图depthV；

　　（2）. 对depthV进行空洞填充；

　　（3）. 利用内参矩阵K和深度图depthV，将虚拟视点图像imgV上的坐标点反向投影到三维空间点，平移后再重投影到参考图像imgL上， 在imgL上利用双线性插值获取imgV上的像素值。

 

　　具体流程如下：

　　（1）. 利用内参矩阵K，以及参考深度图depthL，如下图，将参考图像坐标点(u, v)投影到参考相机的摄像机坐标系下，得到对应的三维空间点(X, Y, Z)，计算方法如下：

d * u =  fx * X + cx *Z
d * v = fy * Y + cy * Z
d = Z

　　其中d是深度值，fx, fy, cx, cy均从内参矩阵中得到，那么(X, Y, Z)可以表示如下：

X = ( u - cx ) * d / fx
Y = ( v - cy ) * d / fy
Z = d

　　参考深度图depthL                                                                            参考左图像imgL

　      

 

　　（2）. 将三维点(X, Y, Z)平移到虚拟摄像机坐标系下，得到虚拟摄像机坐标系下的三维点(X1, Y1, Z1)， 计算如下：

X1 = X - alpha * baseline
Y1 = Y
Z1 = Z

 

　　（3）. 将(X1, Y1, Z1)重投影到虚拟视点图上，得到坐标(u1, v1)：

u1 = ( fx * X1 + cx * d ) / d
v1 = ( fy * Y1 + cy * d ) / d
d = Z1
//注意此处d ！= 0

 

　　利用最近邻插值得到虚拟视点深度图depthV。如下图所示，alpha=0.5位置虚拟视点深度图：

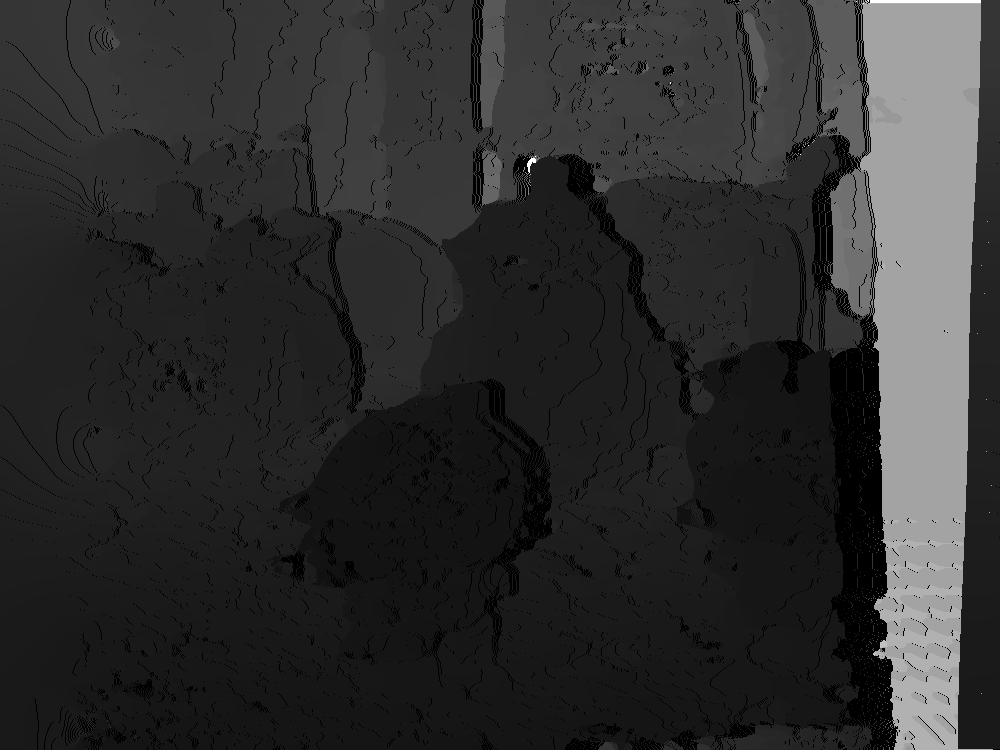
　　（4）. 对depthV进行空洞填充。填充后depthV如下图：

　　（5）. 利用depthV和内参矩阵K，反向重复上述操作。将虚拟视点图像imgV坐标点反向投影到三维点，平移，再重投影到参考视图imgL上，在imgL上利用双线性插值得到imgV上的像素值。从而获取虚拟视点图像imgV，如下图：

　　（6）. 综合上述步骤，可以获取alpha从0 到 1， 也就是从左相机位置到右相机位置的一系列虚拟视点图像，gif动图展示如下：

　上面效果中在深度不连续区域有较为明显的失真，这是由于该区域为遮挡区域，无法计算出准确的视差值，可以通过观察前面立体匹配博客的视差图或者深度图看出。而采用的空洞填充将附近的视差值填充过去，所以会造成前景出现在背景部分，出现较为明显的伪影。去除伪影也有很多种方法，比如结合右参考相机合成同样位置的虚拟视点，然后将两个视点融合等方法。

 

　　其实3D Warping技术的核心就是下面几条语句，二维图像点到三维空间点，平移，旋转，再重投影到新的二维图像点。上面没有加入旋转，旋转的话就是直接用三维点乘以3x3的旋转矩阵后平移，然后再重投影。

float dep = pDepthV[i*imgW + j];
if (dep < 0.001) continue;
//反投影
float X = (j - cx)*dep / fx;
float Y = (i - cy)*dep / fy;
float Z = dep;
//平移
float X2 = X + offsetX;
float Y2 = Y;
float Z2 = Z;
//重投影
float uf = (fx*X2 + cx* Z2) / dep;
float vf = (fy*Y2 + cy * Z2) / dep;