OpenCV亚像素角点cornerSubPixel()源代码分析

　　上一篇博客中讲到了goodFeatureToTrack（）这个API函数能够获取图像中的强角点。但是获取的角点坐标是整数，但是通常情况下，角点的真实位置并不一定在整数像素位置，因此为了获取更为精确的角点位置坐标，需要角点坐标达到亚像素（subPixel）精度。

1. 求取亚像素精度的原理

　　找到一篇讲述原理非常清楚的文档

https://xueyayang.github.io/pdf_posts/%E4%BA%9A%E5%83%8F%E7%B4%A0%E8%A7%92%E7%82%B9%E7%9A%84%E6%B1%82%E6%B3%95.pdf，贴上来，如下：

 2. OpenCV源代码分析

　　OpenCV中有cornerSubPixel（）这个API函数用来针对初始的整数角点坐标进行亚像素精度的优化，该函数原型如下：

void cv::cornerSubPix( InputArray _image, InputOutputArray _corners,
                       Size win, Size zeroZone, TermCriteria criteria )

　　_image为输入的单通道图像；_corners为提取的初始整数角点（比如用goodFeatureToTrack提取的强角点）；win为求取亚像素角点的窗口大小，比如设置Size（11,11），需要注意的是11为半径，则窗口大小为23x23；zeroZone是设置的“零区域”，在搜索窗口内，设置的“零区域”内的值不会被累加，权重值为0。如果设置为Size(-1,-1)，则表示没有这样的区域；critteria是条件阈值，包括迭代次数阈值和误差精度阈值，一旦其中一项条件满足设置的阈值，则停止迭代，获得亚像素角点。

　　这个API通过下面示例的语句进行调用：

cv::cornerSubPix(grayImg, pts, cv::Size(11, 11), cv::Size(-1, -1), cv::TermCriteria(CV_TERMCRIT_EPS + CV_TERMCRIT_ITER, 30, 0.1));

 　　首先看criteria包含的两个条件阈值在代码中是怎么设置的。如下所示，最大迭代次数为100次，误差精度为eps*eps，也就是0.1*0.1。

    const int MAX_ITERS = 100;
    int win_w = win.width * 2 + 1, win_h = win.height * 2 + 1;
    int i, j, k;
    int max_iters = (criteria.type & CV_TERMCRIT_ITER) ? MIN(MAX(criteria.maxCount, 1), MAX_ITERS) : MAX_ITERS;
    double eps = (criteria.type & CV_TERMCRIT_EPS) ? MAX(criteria.epsilon, 0.) : 0;
    eps *= eps; // use square of error in comparsion operations

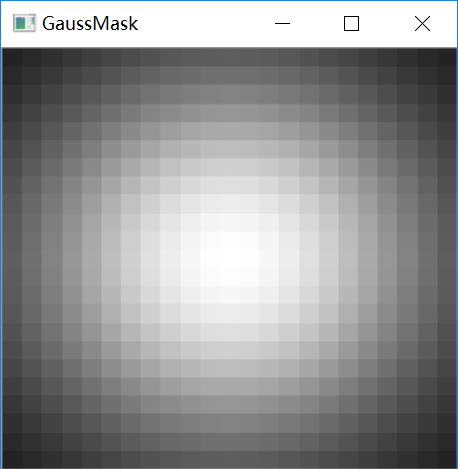
　　然后是高斯权重的计算，如下所示，窗口中心附近权重高，越往窗口边界权重越小。如果设置的有“零区域”，则权重值设置为0。计算出的权重分布如下图：

Mat maskm(win_h, win_w, CV_32F), subpix_buf(win_h+2, win_w+2, CV_32F);
    float* mask = maskm.ptr<float>();

    for( i = 0; i < win_h; i++ )
    {
        float y = (float)(i - win.height)/win.height;
        float vy = std::exp(-y*y);
        for( j = 0; j < win_w; j++ )
        {
            float x = (float)(j - win.width)/win.width;
            mask[i * win_w + j] = (float)(vy*std::exp(-x*x));
        }
    }

    // make zero_zone
    if( zeroZone.width >= 0 && zeroZone.height >= 0 &&
        zeroZone.width * 2 + 1 < win_w && zeroZone.height * 2 + 1 < win_h )
    {
        for( i = win.height - zeroZone.height; i <= win.height + zeroZone.height; i++ )
        {
            for( j = win.width - zeroZone.width; j <= win.width + zeroZone.width; j++ )
            {
                mask[i * win_w + j] = 0;
            }
        }
    }

　　接下来就是针对每个初始角点，按照上述公式，逐个进行迭代求取亚像素角点，代码如下。

　　① 代码中CI2为本次迭代获取的亚像素角点位置，CI为上次迭代获取的亚像素角点位置，CT是初始的整数角点位置。

　　② 每次迭代结束计算CI与CI2之间的欧式距离err，如果两者之间的欧式距离err小于设定的阈值，或者迭代次数达到设定的阈值，则停止迭代。

　　③停止迭代后，需要再次判断最终的亚像素角点位置和初始整数角点之间的差异，如果差值大于设定窗口尺寸的一半，则说明最小二乘计算中收敛性不好，丢弃计算得到的亚像素角点，仍然使用初始的整数角点。

// do optimization loop for all the points
    for( int pt_i = 0; pt_i < count; pt_i++ )
    {
        Point2f cT = corners[pt_i], cI = cT;
        int iter = 0;
        double err = 0;

        do
        {
            Point2f cI2;
            double a = 0, b = 0, c = 0, bb1 = 0, bb2 = 0;

            getRectSubPix(src, Size(win_w+2, win_h+2), cI, subpix_buf, subpix_buf.type());
            const float* subpix = &subpix_buf.at<float>(1,1);

            // process gradient
            for( i = 0, k = 0; i < win_h; i++, subpix += win_w + 2 )
            {
                double py = i - win.height;

                for( j = 0; j < win_w; j++, k++ )
                {
                    double m = mask[k];
                    double tgx = subpix[j+1] - subpix[j-1];
                    double tgy = subpix[j+win_w+2] - subpix[j-win_w-2];
                    double gxx = tgx * tgx * m;
                    double gxy = tgx * tgy * m;
                    double gyy = tgy * tgy * m;
                    double px = j - win.width;

                    a += gxx;
                    b += gxy;
                    c += gyy;

                    bb1 += gxx * px + gxy * py;
                    bb2 += gxy * px + gyy * py;
                }
            }

            double det=a*c-b*b;
            if( fabs( det ) <= DBL_EPSILON*DBL_EPSILON )
                break;

            // 2x2 matrix inversion
            double scale=1.0/det;
            cI2.x = (float)(cI.x + c*scale*bb1 - b*scale*bb2);
            cI2.y = (float)(cI.y - b*scale*bb1 + a*scale*bb2);
            err = (cI2.x - cI.x) * (cI2.x - cI.x) + (cI2.y - cI.y) * (cI2.y - cI.y);
            cI = cI2;
            if( cI.x < 0 || cI.x >= src.cols || cI.y < 0 || cI.y >= src.rows )
                break;
        }
        while( ++iter < max_iters && err > eps );

        // if new point is too far from initial, it means poor convergence.
        // leave initial point as the result
        if( fabs( cI.x - cT.x ) > win.width || fabs( cI.y - cT.y ) > win.height )
            cI = cT;

        corners[pt_i] = cI;
    }

　　

---

 

　　自己参照OpenCV源代码写了一个myCornerSubPix（）接口函数以便加深理解，如下，仅供参考：

//获取窗口内子图像
bool getSubImg(cv::Mat srcImg, cv::Point2f currPoint, cv::Mat &subImg)
{
    int subH = subImg.rows;
    int subW = subImg.cols;
    int x = int(currPoint.x+0.5f);
    int y = int(currPoint.y+0.5f);
    int initx = x - subImg.cols / 2;
    int inity = y - subImg.rows / 2;
    if (initx < 0 || inity < 0 || (initx+subW)>=srcImg.cols || (inity+subH)>=srcImg.rows )   return false;
    cv::Rect imgROI(initx, inity, subW, subH);
    subImg = srcImg(imgROI).clone();
    return true;
}

//亚像素角点提取
void myCornerSubPix(cv::Mat srcImg, vector<cv::Point2f> &pts, cv::Size winSize, cv::Size zeroZone, cv::TermCriteria criteria)
{
　　//搜索窗口大小
    int winH = winSize.width * 2 + 1;
    int winW = winSize.height * 2 + 1;
    int winCnt = winH*winW;

　　//迭代阈值限制
    int MAX_ITERS = 100;
    int max_iters = (criteria.type & CV_TERMCRIT_ITER) ? MIN(MAX(criteria.maxCount, 1), MAX_ITERS) : MAX_ITERS;
    double eps = (criteria.type & CV_TERMCRIT_EPS) ? MAX(criteria.epsilon, 0.) : 0;
    eps *= eps; // use square of error in comparsion operations

    //生成高斯权重
    cv::Mat weightMask = cv::Mat(winH, winW, CV_32FC1);
    for (int i = 0; i < winH; i++)
    {
        for (int j = 0; j < winW; j++)
        {
            float wx = (float)(j - winSize.width) / winSize.width;
            float wy = (float)(i - winSize.height) / winSize.height;
            float vx = exp(-wx*wx);
            float vy = exp(-wy*wy);
            weightMask.at<float>(i, j) = (float)(vx*vy);
        }
    }
　　//遍历所有初始角点，依次迭代
    for (int k = 0; k < pts.size(); k++)
    {
        double a, b, c, bb1, bb2;
        
        cv::Mat subImg = cv::Mat::zeros(winH+2, winW+2, CV_8UC1);
        cv::Point2f currPoint = pts[k];
        cv::Point2f iterPoint = currPoint;

        int iterCnt = 0;
        double err = 0;
        //迭代
        do 
        {
            a = b = c = bb1 = bb2 = 0;
            //提取以当前点为中心的窗口子图像（为了方便求sobel微分，窗口各向四个方向扩展一行（列）像素）
            if ( !getSubImg(srcImg, iterPoint, subImg)) break;
            uchar *pSubData = (uchar*)subImg.data+winW+3;
            //如下计算参考上述推导公式，窗口内累加
            for (int i = 0; i < winH; i ++)
            {
                for (int j = 0; j < winW; j++)
                {
　　　　　　　　　　　　//读取高斯权重值
                    double m = weightMask.at<float>(i, j);
                    //sobel算子求梯度
                    double sobelx = double(pSubData[i*(winW+2) + j + 1] - pSubData[i*(winW+2) + j - 1]);
                    double sobely = double(pSubData[(i+1)*(winW+2) + j] - pSubData[(i - 1)*(winW+2) + j]);
                    double gxx = sobelx*sobelx*m;
                    double gxy = sobelx*sobely*m;
                    double gyy = sobely*sobely*m;
                    a += gxx;
                    b += gxy;
                    c += gyy;
                    //邻域像素p的位置坐标
                    double px = j - winSize.width;
                    double py = i - winSize.height;

                    bb1 += gxx*px + gxy*py;
                    bb2 += gxy*px + gyy*py;
                }
            }
            double det = a*c - b*b;
            if (fabs(det) <= DBL_EPSILON*DBL_EPSILON)
                break;
            //求逆矩阵
            double invA = c / det;
            double invC = a / det;
            double invB = -b / det;
            //角点新位置
            cv::Point2f newPoint;
            newPoint.x = (float)(iterPoint.x + invA*bb1 + invB*bb2);
            newPoint.y = (float)(iterPoint.y + invB*bb1 + invC*bb2);
            //和上一次迭代之间的误差
            err = (newPoint.x - iterPoint.x)*(newPoint.x - iterPoint.x) + (newPoint.y - iterPoint.y)*(newPoint.y - iterPoint.y);
            //更新角点位置
            iterPoint = newPoint;
            iterCnt++;
            if (iterPoint.x < 0 || iterPoint.x >= srcImg.cols || iterPoint.y < 0 || iterPoint.y >= srcImg.rows)
                break;
        } while (err > eps && iterCnt < max_iters);
        //判断求得的亚像素角点与初始角点之间的差异，即：最小二乘法的收敛性
        if (fabs(iterPoint.x - currPoint.x) > winSize.width || fabs(iterPoint.y - currPoint.y) > winSize.height)
            iterPoint = currPoint;
　　　　//保存算出的亚像素角点
        pts[k] = iterPoint;
    }
}

　　夜已深，结束。