【题解】CF1279F New Year and Handle Change

标签：DP \(B\)

这道题，我们显然首先分开考虑尽量变成大写字母和小写字母的情况。

对于这道题目，想必首先想到的是一道简单的 dp

设 \(f_{i,j}\) 表示前 \(i\) 个字符，使用的 \(j\) 次赋值后的最少大/小写个数。

但是我们发现，这个状态是 \(O(nk)\) 的，而转移可以通过 前缀和+差分 的方式做到 \(O(1)\)

但是显然这是不能过的。

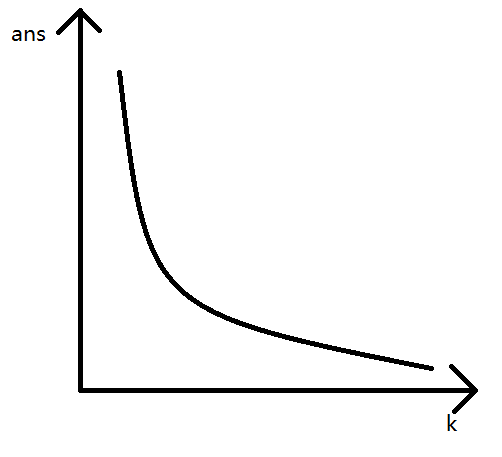
但是我们发现我们最后的答案对于 \(k\) 的取值是呈凸性的，这就可以 wqs 二分了。

我们首先可以画出答案和 \(k\) 的函数图像：

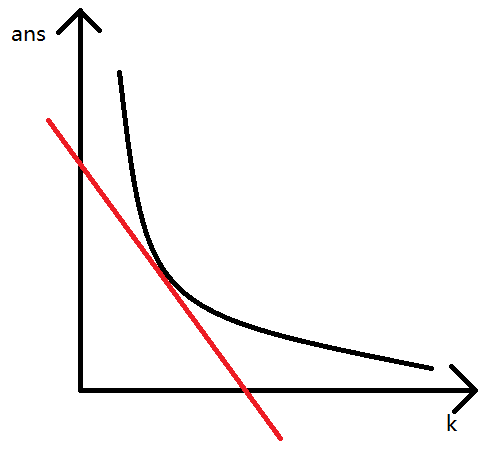
然后像 wqs二分 斜率，再通过 DP 找到相切的点，根据相切的点的横坐标进行斜率的调整。

code:

#include<bits/stdc++.h>
using namespace std;
const int NN = 1e6 + 8;
int n,k,l;
int ans;
bool a[NN];
char s[NN];
int f[NN],g[NN];
int check(int mid){
	for(int i = 1; i <= n; ++i){
		f[i] = f[i-1] + a[i]; g[i] = g[i-1];
		if(f[max(i-l,0)] - mid < f[i]){
			f[i] = f[max(i-l,0)] - mid;
			g[i] = g[max(i-l,0)] + 1;
		}
	}
	return g[n];
}
void solve(){
	int l = -n,r = 0,res = 0;
	while(l <= r){
		int mid = (l + r) / 2;
		if(check(mid) <= k) l = mid + 1,res = mid;
		else r = mid - 1;
	}
	check(res);
	ans = min(ans,f[n] + res * k);
}
int main(){
	ans = 0x3f3f3f3f;
	ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);
	cin >> n >> k >> l;
	cin >> s+1;
	for(int i = 1; i <= n; ++i) a[i] = 'A' <= s[i] && s[i] <= 'Z';
	solve();
	for(int i = 1; i <= n; ++i) a[i] = !a[i];
	solve();
	cout << ans << '\n';
}